复杂工况下大位移井岩屑运移与参数优化研究*

朱 娜 黄文君 高德利

(中国石油大学(北京)石油工程教育部重点实验室)

0 引 言

大位移井是在定向井、水平井和深井基础上发展起来的一种新型钻井技术，集中了各种常规井型的技术难点，代表了钻井技术发展的最新高度[1-2]，而井眼净化是大位移井钻井过程中面临的重要难题之一[3-7]。研究结果显示，不同地区发生卡钻事故的主要原因不同[8]，根据拉丁美洲作业统计，65%的事故原因是井眼净化不充分[9-10]；而钻井工况对卡钻的影响也非常大，起下钻时卡钻发生的比例很高，可能高达90%[8]。A.A.ALSHAIKH等[11]还发现，接单根、倒划眼、钻进和起钻是最常见的卡钻工况，比例分别为28%、18%、14%和13%。准确预测复杂工况下岩屑床的运移和分布对降低和控制卡钻风险具有重要意义。

目前研究岩屑运移的方法主要分为3种[12-15]：试验法、有限元仿真法和分层模型法，这3种方法各有优缺点。其中，试验法的优点是可以通过测量直接得到岩屑的浓度，但是不便于模拟复杂工具以及全井筒中岩屑的运移规律。有限元仿真软件Fluent能够精细地模拟各种工具，比如岩屑床破坏器作用下颗粒的运移和分布，但是其计算时间相对较长，所以现有的仿真模型长度主要集中在数十米。分层模型法包括两层模型和三层模型，计算速度较快，在模拟全井段的岩屑床分布有明显的优势。

但是，无论是上述哪种方法，主要研究的工况都是钻进或者洗井2种，而关于停泵和起下钻工况的研究非常少。在试验法中，一般是假设从入口以一定排量和浓度注入液体和岩屑颗粒，然后研究环空中颗粒的浓度分布[13]。本质上，这是一种钻进工况；而分层模型法中，先假设环空中分布一定高度的岩屑床，然后研究不同排量和不同偏心度等参数下岩屑高度减小的规律[14]，这种情况本质是洗井工况。而停泵时，由于钻井液的悬浮力不足，岩屑床可能停止向上运移，甚至向下滑动，并且堆积在大斜度井段，形成了卡钻风险。准确预测停泵状态下岩屑床堆积的高度和位置对井眼净化有很重要的指导意义。另一方面，在现有模型中，无论是钻进还是循环状态下，都是假设钻杆不动，此时钻杆对岩屑床和悬浮层的摩擦力为阻力。当起下钻时，钻杆的作用力有可能会变成动力。此时，传统的两层动态岩屑床运移模型将不能完全适用，需要对钻杆的受力进行修正。

本文拟建立适用于停泵和起下钻工况的两层动态岩屑床运移模型，并分析钻进、洗井、停泵以及起钻的组合工况下岩屑床的动态运移规律，以期为提高大位移井作业井眼净化效果提供理论指导。

1 岩屑床动态运移模型

1.1 复杂工况下两层动态岩屑床运移模型的概念

目前现有的两层动态岩屑床运移模型主要基于钻进和洗井2种工况，并不完全适用于停泵和起下钻的复杂工况，因为受力关系发生了变化，具体分析如下。

1.1.1 钻井和洗井工况

岩屑床在钻井液剪切力的携带下，由井底运移至井口。对于悬浮层，重力和岩屑床提供的剪切力均为阻力。现有的两层动态岩屑床运移模型通过建立和求解动量守恒和质量守恒方程，可以模拟这两个过程。

1.1.2 停泵

与上述2种工况相反，停泵时，岩屑床在重力的作用下从井口下滑。

对于悬浮层，重力和岩屑床提供的剪切力变成了动力。由于岩屑床层和悬浮层的受力关系均发生了变化，两层动态岩屑床运移模型的动量方程也需要进行完善。

1.1.3 起下钻

在现有模型中，无论是钻进还是循环状态下，都是假设钻杆不动，此时钻杆对岩屑床和悬浮层的摩擦力为阻力。当起下钻时，钻杆的作用力有可能会变成动力。比如开泵起钻、倒划眼起钻或者停泵下钻，如果起下钻速度大于岩屑床和悬浮层的运移速度，那么钻杆对两层的运移提供动力。此时，传统的两层动态岩屑床运移模型将不能适用，需要对钻杆的受力进行修正。

1.2 两层动态岩屑床运移模型的基本假设

两层模型示意图如图1所示，模型的基本假设如下[16-18]：

图1 钻进、循环和停泵工况下岩屑运移两层模型示意图Fig.1 Schematic diagram of two-layer cuttings migration model under the conditions of drilling,circulation and pump stop

(1)上层为悬浮层，包括岩屑固相和钻井液液相；

(2)下层为岩屑床，此层中的岩屑体积分数假定为52%；

(3)固液体系均为不可压缩介质，固体颗粒具有相同的直径和圆球度；

(4)不考虑温度变化的影响。

1.3 钻井和洗井工况下的两层动态岩屑床运移模型

在上述假设条件下，根据流体力学理论，运用质量守恒定律和动量定理推导出了岩屑床层、悬浮层的连续性方程和运动方程，此方程为一阶偏微分方程组[19-20]，其中悬浮层中液相、固相以及岩屑床层的动量方程分别为：

(1)

悬浮层中液相、固相以及岩屑床层的连续性方程为：

(2)

式中：A为面积，m2；C为体积分数，无因次；v为速度，m/s；ρ为密度，g/cm3；p为压力，Pa；τ为剪切力，Pa；S为润湿周长，m；F为干摩擦力，N；FCF为固体颗粒和液体之间的拖曳力，N；θ为井斜角，(°)；g为重力加速度，m/s2；ФSF为悬浮层固相变化质量，kg；ФSC为悬浮层液相变化质量，kg；ФBS为岩屑床固相变化质量，kg；ξF、ξC、ξB为考虑浮力作用之后的修正系数；下标S、B、I、F、C分别代表悬浮层、岩屑床层、悬浮层与岩屑床的相界面、悬浮层中的液相、悬浮层中的固相。

由上可知，此模型需求解8个未知数:AS、AB、vC、vF、vB、CC、CF和p，以上有6个方程不足以实现求解，需要添加2个辅助方程：

AB+AS=AT

(3)

CC+CF=1

(4)

式中：AT为环空总截面积，m2。

由于模型方程组非线性较强，未知数之间还存在耦合，所以引用GUO X.L.等[21]的SETS方法求解。

1.4 停泵工况下的两层动态岩屑床运移模型

在停泵工况下，由于钻井液的悬浮力不足，岩屑床可能停止向上运移，甚至向下滑动(见图1c)。此时，动量方程中的受力关系与钻井和循环工况不同。其中，重力变成了岩屑运移的动力，悬浮层的剪应力变成了阻力。因此，两层模型的动量守恒方程需要进行修正。

悬浮层中液相、固相及岩屑床层的动量方程为：

(5)

停泵工况下的质量守恒方程与方程(2)一致。

其中，式(5)中岩屑床的摩擦力为滑动摩擦，即岩屑床已经向下滑动时与井壁之间的摩擦力。但是事实上，岩屑床并不是一直在滑动，而是有可能在大井斜角的井段停止下滑，并且产生堆积。在这种情况下，摩擦力是静摩擦。岩屑床开始滑动的判断条件是静干摩擦力(FSTA)达到最大干摩擦力(FMAX)[22]。当满足以下条件时，岩屑床保持静止[23-24]：

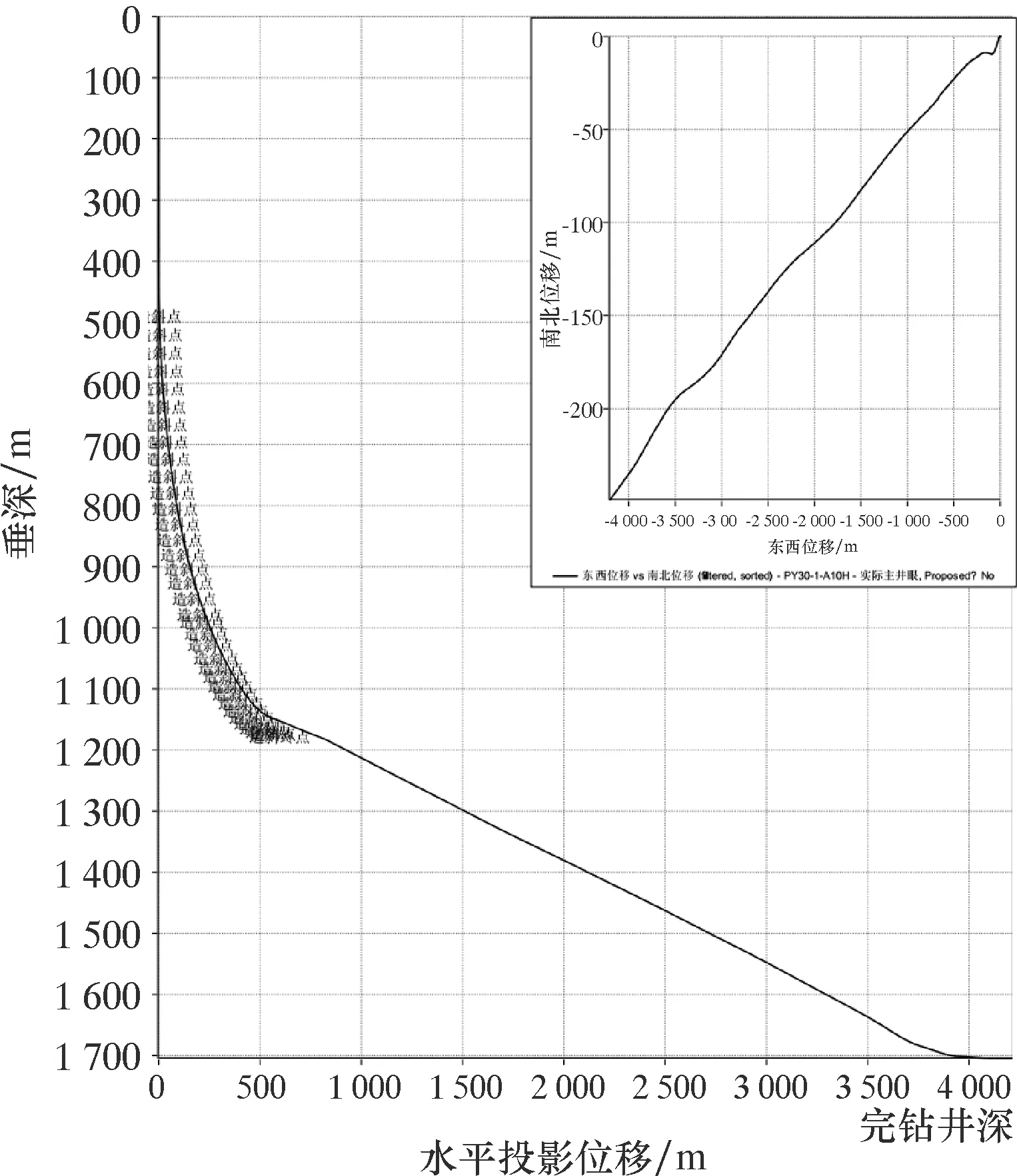
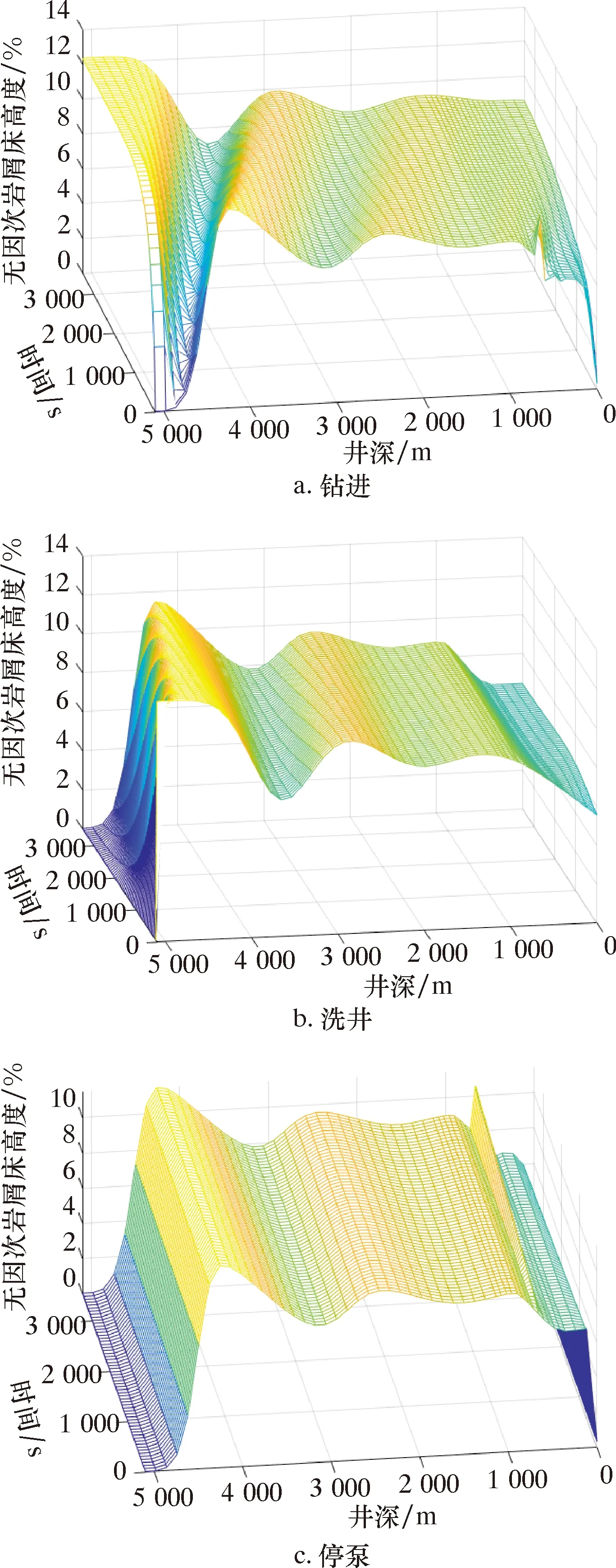
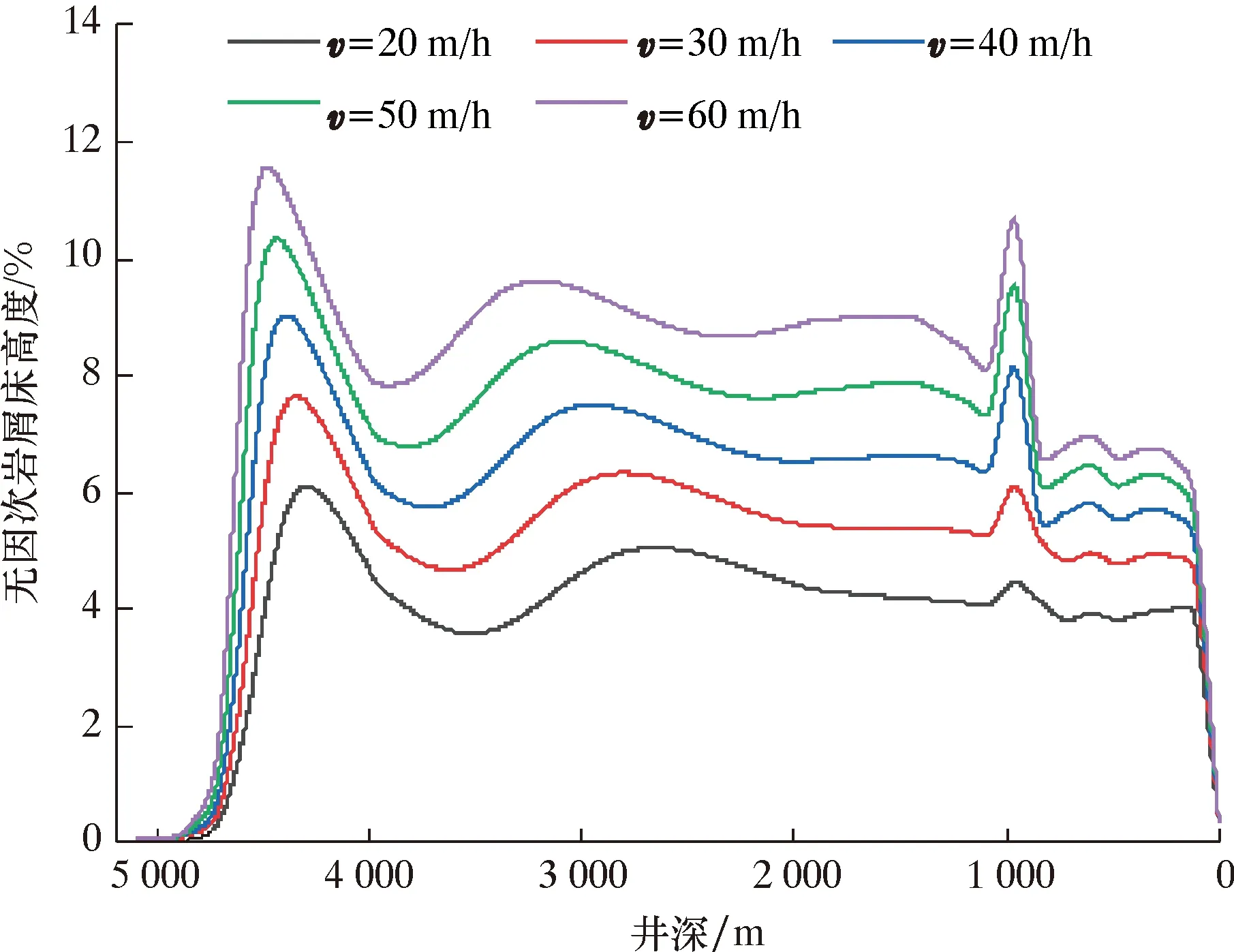
FSTA

(6)

静摩擦的准确计算对于预测停泵时岩屑床的堆积位置和高度至关重要，其计算方法如下：首先，当岩屑床从静止状态开始下滑时，假设岩屑床的初始速度为0，即vB≈0。则由质量方程可知：

(7)

然后，将上述方程代入到动量方程组(5)中，可以得出：

(8)

因此，由方程组(8)消元，可以得到静摩擦力的计算方程：

ρBABgξBcosθ+τISI

(9)

特殊地，当悬浮层的初始速度也为0时，上式可以简化为：

FSTA=(ρFgξF-ρBgξB)ABcosθ

(10)

方程式(9)可以用来计算岩屑床的休止角(即将含有岩屑床和悬浮层的管柱，从水平面上逐渐向上抬起，岩屑床开始下滑的角度)。因此，当静摩擦力达到最大摩擦力时，岩屑床开始向下滑动。

1.5 起下钻工况下的两层动态岩屑床运移模型

通常，钻杆有3种运动状态，即向上运动、向下运动和静止。这3种状态的主要区别在于，钻杆对岩屑床层以及悬浮层的剪切力方向不同。更具体地说，当钻杆静止时，如果开泵循环，那么钻杆对于岩屑床和悬浮层都产生了阻力。当起钻时，如果停泵，岩屑床下滑，那么钻杆对于岩屑床和悬浮层提供的也是阻力；反之，开泵起钻，比如倒划眼工况，钻杆提供的可能是动力或者是阻力，取决于钻杆与两层之间的相对速度。同理，下钻时，钻杆提供的可能是动力或者是阻力，与下钻速度和岩屑床、悬浮层的相对速度相关[25]。

但是，目前的两层模型通常假设钻杆处于静止状态，无论是钻进还是循环，钻杆对两层的剪切力均为阻力。因此模拟起下钻工况时，如果钻杆提供的是动力，那么动量方程也会发生变化，可以通过改变动量方程中的润湿周长来进行修正。王文广和ZHU N.等[26-27]根据岩屑高度和钻杆的位置，将两层模型的截面图分为了5种，并且分别推导了其几何关系式。以其第2种几何关系式为例，当钻杆对岩屑床层和悬浮层提供的作用力为阻力时，也是现有的两层动态岩屑运移模型采用的计算方法，岩屑床层和悬浮层的润湿周长如下：

(11)

当钻杆对岩屑床层和悬浮层提供的作用力为动力时，岩屑床层和悬浮层的润湿周长修正如下：

(12)

式中：d1为井眼内径，m；d2为钻杆外径，m；α为环空岩屑床面相对于井眼中心的圆心半角，rad；β为环空岩屑床面相对于钻杆中心的圆心半角，rad。

2 岩屑床动态运移规律分析

图3 X-1井井身结构示意图Fig.3 Casing program of Well X-1

X-1井为南海油田某大位移井，其井眼轨迹和井身结构见图2、3，实际完钻井深5 117.00 m，水平位移4 211.24 m，垂深1 704.46 m，水垂比为2.47。在施工中遇到的典型问题包括倒划眼困难，频繁憋泵、憋扭矩，憋泵引起ECD瞬时升高压漏地层，由于井漏和卡钻的出现，导致整个施工周期长于设计周期，严重影响了作业时效，同时给作业带来很大风险。分析认为该大位移井大斜度段(井斜角80°，长3 240 m)中岩屑沉积形成岩屑床，导致部分井壁失稳，井径扩大，存在部分“扩径”形成了“台阶”，且加剧了岩屑床的堆积。因此，基于岩屑床运移两层动态模型对X-1井进行计算，模拟该井的岩屑床分布。

图2 X-1井井眼轨迹图Fig.2 Well trajectory of Well X-1

2.1 复杂工况下的岩屑床的分布规律

采用两层岩屑床动态运移模型模拟复杂工况下岩屑床的分布规律，包括钻进、洗井、停泵的交替工况以及起钻。其中，钻进和洗井时间分别为1 h，排量为30 L/s，机械钻速为60 m/h。

首先模拟第1个钻进、洗井、停泵的交替工况，在环空初始岩屑床高度为0的条件下，钻进1 h，模拟结果如图4所示。由图4可见，在钻头附近形成了一个小砂丘，最大无因次岩屑床高度为12.3%，砂丘长度约为1 500 m。然后在此基础上洗井1 h，可见，砂丘的数量保持不变，在钻井液的冲洗作用下，向前运移了约700 m。在此基础上停泵、接单根，此时斜井段的岩屑堆积并不明显，原因是岩屑床还没有运移至斜井段。

图4 第1次钻进、洗井、停泵的交替工况下岩屑床高度分布图Fig.4 Distribution of cuttings bed height with the alternation of the first drilling,washing and pump stop

在上述岩屑分布的基础上，模拟第2个钻进、洗井、停泵的交替工况组合，模拟结果如图5所示。由图5可见，在钻头处形成了第2个砂丘。砂丘无因次高度为12.3%，长度约为1 500 m。第一个砂丘的波峰已经向前运移到了井深3 000 m处。然后洗井循环1 h之后，2个砂丘均朝井口方向运移，同时高度也有所减小。第1个形成的砂丘无因次高度由12.3%减小为9.8%。在此基础上停泵，可以看出岩屑下滑至第二洗井区，但是高度较小，为4.1%，因为此时2个砂丘的波峰尚未运移至第二洗井区。

图5 第2次钻进、洗井、停泵的交替工况下岩屑床高度分布图Fig.5 Distribution of cuttings bed height with the alternation of the second drilling,washing and pump stop

在上述岩屑分布的基础上，模拟第3个钻进、洗井、停泵的交替工况组合,模拟结果如图6所示。由图6可见，钻进1 h之后在钻头处形成了第3个砂丘，洗井1 h后，形成的第1个砂丘已经运移至井口，此时第二洗井区的无因次岩屑床高度约为7.9%。在此基础上停泵，岩屑下滑产生堆积，其最高堆积的无因次岩屑床高度约为10.1%，可见初始岩屑高度越大，停泵时堆积高度越高。

图6 第3次钻进、洗井、停泵的交替工况下岩屑床高度分布图Fig.6 Distribution of cuttings bed height with the alternation of the third drilling,washing and pump stop

第4次钻进、洗井、停泵的交替工况下岩屑床高度的分布如图7所示。由图7可见，其与第3次交替工况下岩屑床分布基本一致原因是岩屑已经运移出井口，留在井筒中的岩屑分布达到了动态稳定，并且大斜度井段内大约每2 000 m形成了一个砂丘。以此类推，当钻进500 m时(以钻进500 m井段进行短起下作业为例)，大约需要进行8个上述工况的循环，岩屑分布和图7基本一致。然后在其基础上模拟起钻工况下的岩屑床分布(见图8)，其中起钻速度是0.5 m/s，接头直径260 mm。由图8可知，在接头作用下形成了无因次高度约为15.0%的小砂丘，会造成起钻遇阻。如果要保证起钻顺畅，应该继续循环洗井，使井筒中的波浪状岩屑床清洗至安全值(无因次岩屑床高度小于10.0%)。

图7 第4次钻进、洗井、停泵的交替工况下岩屑床高度分布图Fig.7 Distribution of cuttings bed height with the alternation of the fourth drilling,washing and pump stop

图8 起钻时岩屑高度分布图Fig.8 Distribution of cuttings bed height during tripping out

井筒内岩屑床呈波浪式分布，相应地，洗井时岩屑的返排也呈现间断式。更具体地，当离井口较近的砂丘返排时，地面会出现一次较大的“岩屑潮”[28]，当该砂丘完全运移出井口后，振动筛会暂时干净，此时如果认为井眼净化而起钻，将会很容易发生卡钻(这也是目前大位移井钻井施工时，起钻遇阻并转为倒划眼起钻的一个很重要的因素)，所以此时应该继续洗井，直到地面出现第2次和第3次“岩屑潮”，也就是井筒内的砂丘被清洗干净。

2.2 排量的影响

以钻进、洗井、停泵工况的交替4个循环为例，不同洗井排量下岩屑床的无因次高度分布如图9所示。排量Q的变化范围是30～65 L/s。分析结果表明，排量越大，大斜度井段的无因次岩屑床高度越小，井眼清洗效果越好。流量为30和65 L/s时，最高无因次高度分别为11.7%和10.5%，同时岩屑床整体向井口处移动了约1 000 m，更有利于岩屑床的返排。而岩屑床在停泵时下滑堆积的高度并不与排量成反比。原因是岩屑床并非以一个均匀的高度分布，而是呈波浪状。岩屑下滑的堆积高度与初始岩屑高度成正比。具体地说，当排量为65 L/s时，岩屑床的波峰运移至第二洗井区；而当排量为30 L/s时，波峰还没有运移到第二洗井区。

图9 排量对无因次岩屑床高度的影响Fig.9 Influence of displacement on the dimensionless height of cuttings bed

2.3 机械钻速的影响

以钻进、洗井、停泵工况的交替4个循环为例，不同机械钻速下岩屑床的无因次高度分布如图10所示。机械钻速v的变化范围是20～60 m/h。分析结果表明：当机械钻速为60 m/h时，岩屑床的最高无因次高度11.7%；而当机械钻速为20 m/h时，最高无因次高度6.0%。由此可见，机械钻速越高，岩屑床整体高度越大；同时，岩屑床在停泵时下滑堆积至第二洗井区时，其堆积高度也与机械钻速呈正相关。

图10 机械钻速对无因次岩屑床高度的影响Fig.10 Influence of ROP on the dimensionless height of cuttings bed

3 结 论

(1)本文建立的大位移井复杂工况下岩屑床动态运移模型可以模拟钻进、洗井、停泵及起钻工况下岩屑床的动态分布。模拟结果表明，在机械钻速为60 m/h、排量为30 L/s时，随着钻进、洗井、停泵工况的交替，大斜度井段内大约每2 000 m形成一个砂丘。相应地，地面返排的“岩屑潮”数量也和井筒内砂丘相对应。第1个“岩屑潮”返排后，振动筛暂时的干净不能表征井眼已经净化，此时起钻将很容易发生卡钻，所以此时应该继续洗井，直到地面出现第2次或更多次的“岩屑潮”，即井筒内的砂丘均运移至地面。

(2)在其他参数一致时，排量越大，岩屑床沿井口方向运移的位移越大，大斜度井段的无因次岩屑床的高度越小。但是在停泵工况下，第二洗井区处岩屑床下滑堆积的高度并不与排量成反比，而是和停泵之前的初始岩屑高度成正比。

(3)机械钻速越高，岩屑床的整体高度越大，同时斜井段处岩屑床在停泵时下滑堆积，其堆积高度也与机械钻速呈正相关。