基于特征值和弧长法计算套管抗挤强度*
2022-03-30张哲平杨尚谕王雪刚
张 旭, 张哲平, 杨尚谕, 王雪刚, 宋 琳
1天津钢管制造有限公司 2中国石油集团工程材料研究院有限公司 3石油管材及装备材料服役行为与结构安全国家重点实验室 4中国石油新疆油田公司工程技术研究院
0 引言
随着页岩气、煤层气开采规模逐渐加大[1- 4],套损问题变得尤为突出[5- 9],页岩气及煤层气在压裂过程中经常发生套管变形现象,损坏了井筒结构的完整性,影响后续压裂及生产作业。因此,摸清套管的真实服役状态,提供安全可靠的管材性能,避免安全系数过剩,有助于进行科学的固井设计选材。
国内诸多学者对套管的抗外挤额定值做了研究,韩建增等[10]给出了一种考虑套管几何尺寸的抗挤毁计算公式,但该公式依据弹性力学推导无法计算后屈曲行为;孙坤忠[11]引用了K-T公式,该公式同样不能计算套管的后屈曲行为;曾义金等[12]研究了盐膏层蠕变产生的挤压应力随时间的变化,没有给出套管抗挤毁性能的评价方法;申照熙等[13]研究了影响套管抗挤毁性能的因素,并给出了计算公式,但没有考虑到塑形套管挤毁过程的后屈曲行为;覃成锦等[14]分析了不同应力状态对套管抗挤毁性能的影响,仇伟德等[15]深入分析了影响抗挤毁性能的各项因素,但没有给出计算公式;张月敏等[16]介绍了TP130TT高抗挤毁套管的成功应用,在使用过程中存在下入磨阻大问题。因此,准确快速计算套管的抗挤毁值,可以加强对套管性能认识,避免过度设计,降低材料消耗,所以如何有效评价套管的抗挤毁性能成为一个关键问题。当外压逐渐增大,套管发生屈服变形,随着变形量的增加,套管抗挤毁能力提高(见图1),第一次变形称为线性特征值屈曲或前屈曲;第二次变形称为非线性屈曲或后屈曲[17- 18]。
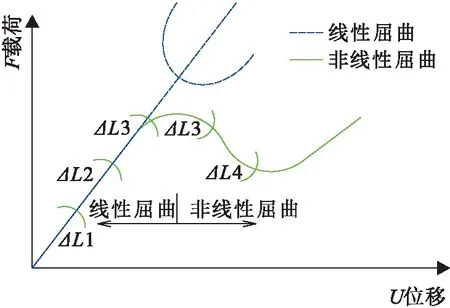
图1 载荷位移响应示意图
实际生产、运输储存、使用过程不可避免地存在缺欠,或为材料缺欠或为几何缺欠,这种缺欠按照API 5CT也是允许存在的,而API 5C3对此处理较为粗糙,通过线性及非线性分析方法可以较好的解决该问题。
1 套管的线性屈曲分析
套管的线性特征值屈曲,其线弹性屈曲载荷{P0}与位移{U0}关系:
[Ke]{U0}={P0}
(1)
式中:[Ke]—弹性刚度矩阵;
U0—由{P0}引起的位移;
{σ}—与{U0}对应的应力。
在任意状态下的增量平衡方程:
{ΔP}=([Ke]+[KG(σ)]){ΔU}
(2)
式中:[KG(σ)]—初始应力矩阵。
假设线弹性屈曲是一个外加载荷{P0}的线性函数,即:
{P}=λ{P0}
{U}=λ{U0}
{σ}=λ{σ0}
则,可得:
[KG(σ)]=λ[KG(σ0)]
(3)
因此,其增量平衡方程变为:
{ΔP}=([Ke]+λ[KG(σ0)]){ΔU}
(4)
当发生线性屈曲时{ΔP}=0,于是式(4)变为:
([Ke]+λ[KG(σ0)]){ΔU}={0}
(5)
那么必须有det{[Ke]+λ[KG(σ0)]}=0,由该方程解出关于λ的n阶多项式,解出最小特征值λ,λ代表临界抗挤毁载荷比例因子,最小特征值乘以初始载荷得到临界载荷,即抗挤毁值。线性特征值分析对于解决线弹性变形问题可以提供较好的解决方案,但是对于屈曲及后屈曲问题计算结果偏大,为此需要进行弧长法分析。实际分析当中,对于径壁比较大套管,使用线性特征值分析即可得到准确解;对于径壁比较小的套管需要采用两种方法进行计算分析。
2 弧长法计算套管的抗挤毁强度
2.1 弧长法计算理论分析
通过引用弧长因子(ΔL),将载荷因子λ和位移增量{ΔU}相联系,弥补了Newton-Raphson方法极值点发散的缺点,可以精确求解后屈曲载荷,求解示意图如图1所示。
弧长法增量平衡迭代方程:
(6)
(7)
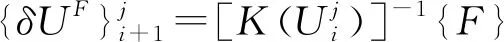
(8)

(9)
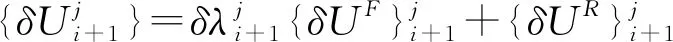
(10)
曲面控制弧长法约束方程可表述为:
(11)
令α=1,当β=1时,为球面弧长法;当β=0时,为柱面弧长法。当β=当前刚度数值时,为椭球面参数法。
下面以柱面弧长法为例,进行阐述说明,其约束方程为
(12)
第i+1载荷步的位移增量关系为:
(13)
将式(10)带入式(13),得:
(14)
将式(14)带入式(12),得:
(15)
(16)
(17)
(18)
2.2 模型及其参数
选取油气井常用的典型规格套管进行建模计算,套管规格及材料参数见表1,模型参数长度2 000 mm。模型的分析单位类型为C3D8R,即8结点线性六面体单元,网格划分在壁厚方向上分三层,对管体两端进行全约束,如图2所示。

图2 约束载荷施加情况
2.3 特征值计算
首先采用特征值分析方法对模型进行线性分析,加载方式为施加均布外压载荷,分析采用六阶特征值方法,取第一阶结果作为后续分析的模型如表1所示。一阶结果如表2所示。
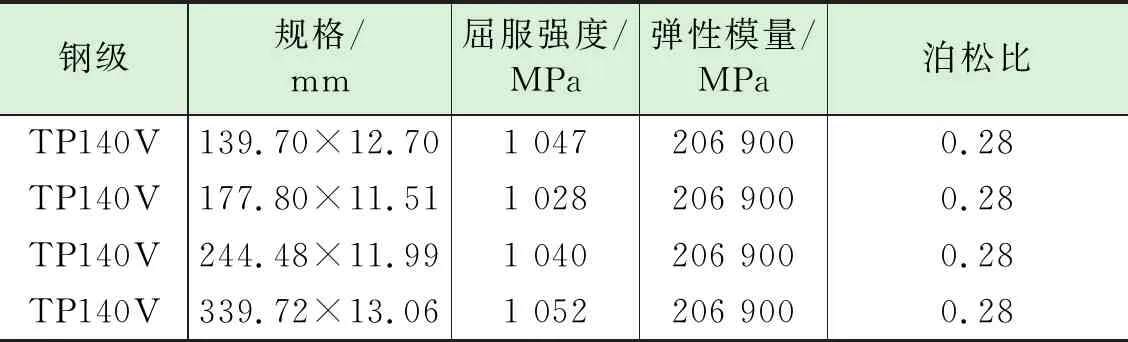
表1 套管规格及材料参数
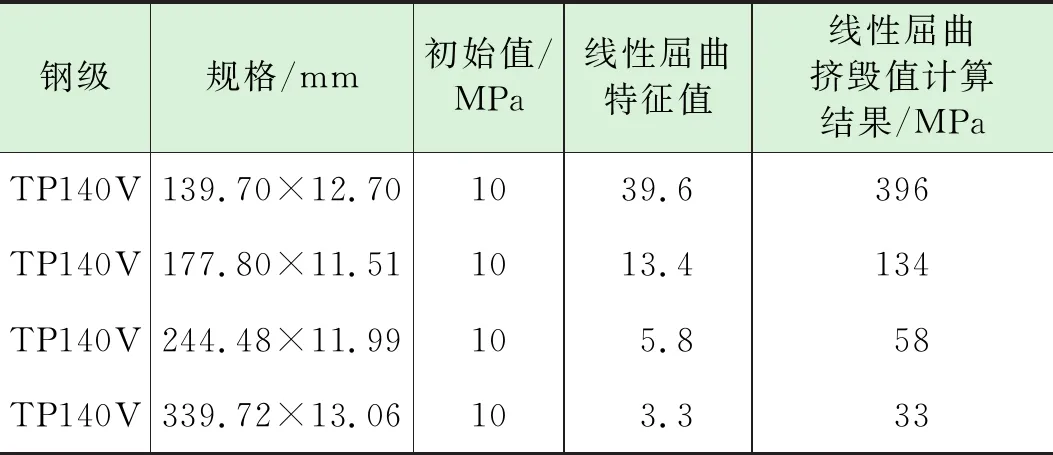
表2 线性屈曲计算结果
2.4 非线性屈曲分析
取线性分析结果的一阶模态进行后屈曲分析,考虑壁厚的5%作为缺欠进行缺欠敏感性分析。计算结果如表3所示,各个不同规格的套管计算结果与实物试验挤毁值比较可见,计算误差在3%左右。通过与表2的线性屈曲计算结果相对比,特征值计算结果对于弹性挤毁套管计算较为准确,但是对于塑形挤毁套管结果明显偏大,说明线性分析存在局限性。虽然线性分析计算的结果偏大,但其可作为非线性分析的基础模态,使非线性分析计算更为准确。高度接近实物试验结果说明弧长法计算套管抗挤强度具有可行性。
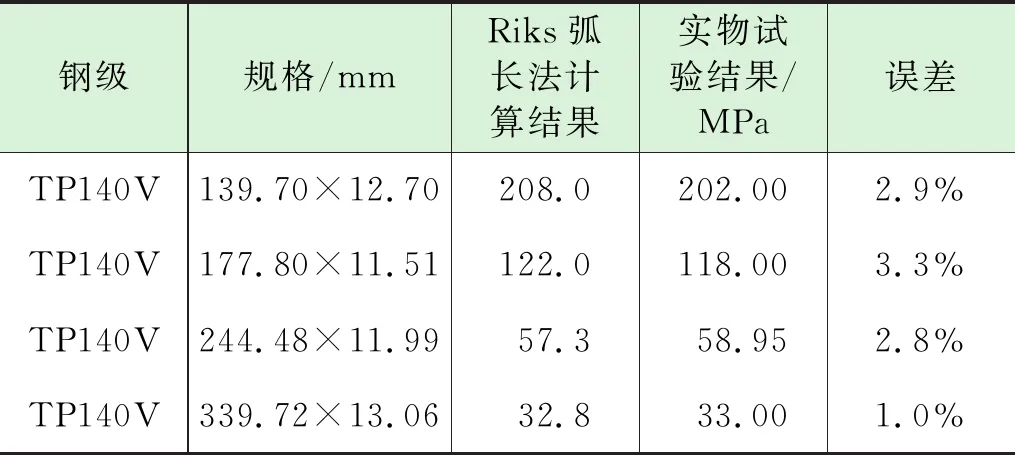
表3 非线性分析计算结果
3 材料缺欠和弯曲度对抗挤性能的影响
3.1 弯曲度对抗挤毁性能的影响
以Ø139.7 mm×12.70 mm进行建模。管体两端全约束,管体中间通过刚体施加位移,模型及推弯过程如图3所示。
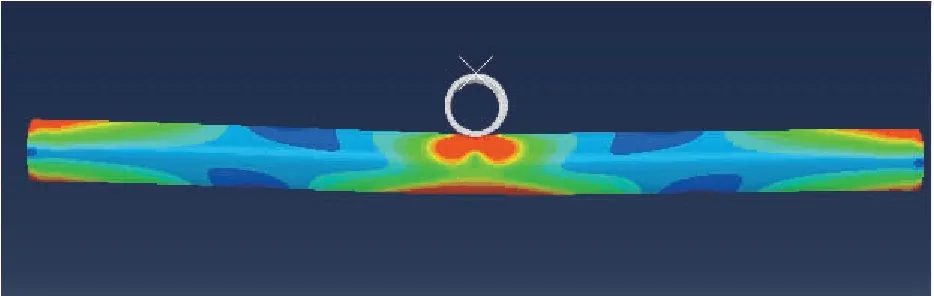
图3 推弯状态
3.2 材料缺欠对抗挤性能的影响
套管自身存在的缺欠一定程度上影响套管的抗挤毁性能,为此对模型施加不同的缺欠模态,分别为壁厚的5%、10%、15%,初始载荷保持不变,计算结果如表4,不同规格的套管随着缺欠模态的增加,lpf载荷比例因子逐渐减小,即套管抗挤毁性能逐渐降低,表明缺欠模态的增加降低套管的抗挤毁性能。
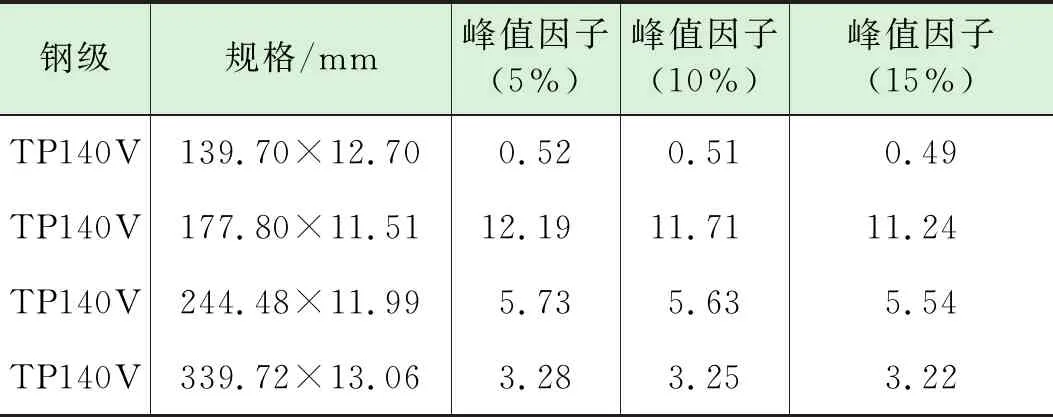
表4 有限元计算峰值因子
套管串在井下随井眼轨迹增、降斜作业存在弯曲状态,建模时通过在套管中间部位施加不同的位移,使其产生不同的弯曲度,分别为8°/30 m、16°/30 m、25°/30 m、41°/30 m。采用弧长法计算套管的抗挤毁性能,弯曲应力叠加局部应力集中导致套管抗挤毁性能降低,8°/30 m的弯曲度导致抗挤毁性能降低5%左右,到41°/30 m的抗挤毁性能降低35%,如图4所示。通过弧长法可以有效表征套管在弯曲度存在的条件下抗挤毁强度损失情况,如图5所示。
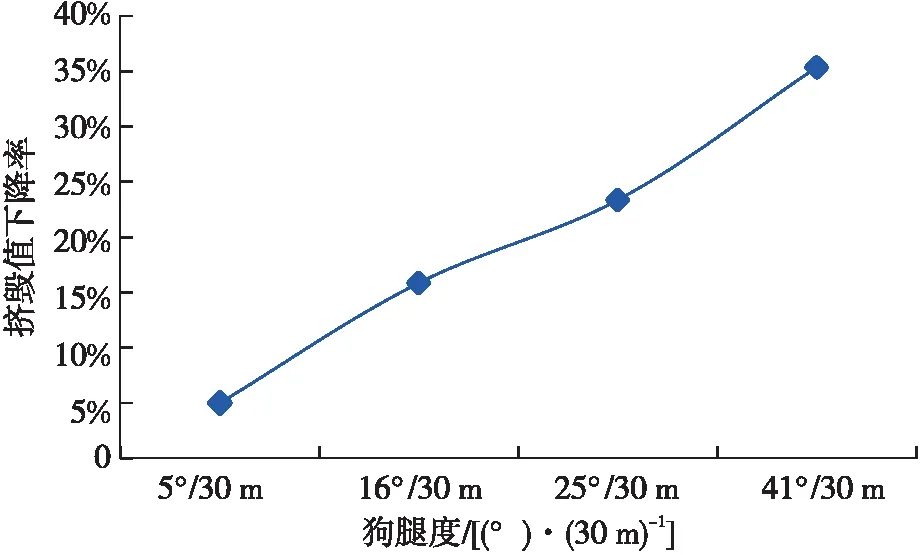
图4 弯曲度与挤毁值的关系

图5 挤毁状态
4 实物试验与有限元计算对比
该分析方法可以准确的计算钢管的后屈曲行为及其结果,对比图6~图9发现钢管压溃的FEA模拟形貌和实物试验形貌一致,具有高度吻合性,即弹性挤毁套管发生弹性失稳变形,变形部位呈现微椭圆状态;塑形挤毁套管发生后屈曲变形,变形部位呈现挤毁形貌。结合数值比较和形貌比较,说明该方法可用于套管的计算分析。

图6 FEA模拟失效形貌图及实物挤毁图(Ø139 mm×12.70 mm)

图7 FEA模拟失效形貌图及实物挤毁图(Ø177 mm×11.51 mm)

图8 FEA模拟失效形貌图及实物挤毁图(Ø244 mm×11.99 mm)

图9 FEA模拟失效形貌图及实物挤毁图(Ø399 mm×13.06 mm)
结合表3数据说明,对于大尺寸套管以及处于弹性挤毁范围的中度尺寸的套管可采用线性特征值分析直接进行计算,其计算结果与Riks弧长法计算结果很接近,可以忽略两者的差别。
5 结论
(1)特征值和弧长法计算可以有效计算套管的抗挤毁值。对于弹性挤毁套管,可直接用线性屈曲分析计算;对于塑形挤毁套管需要在线性屈曲分析的基础上采用弧长法进行计算。
(2)通过有限元计算与实物试验对比分析,单轴载荷条件下,套管挤毁值与实物试验结果一致,且FEA模拟失效形貌与实物试验失效形貌一致。
(3)随着缺欠模态的增加,lpf载荷比例因子逐渐减小,套管挤毁值逐渐降低;弯曲度显著影响挤毁值,随着弯曲度增大,套管抗挤毁能力逐渐降低。钻井过程中应加强井眼轨迹控制,防止局部出现狗腿度过大现象。
