地层空洞影响下地铁盾构隧道衬砌结构响应试验研究

管锋，魏度强，雷金山，石钰锋,4，曹成威

(1. 中国铁路南昌局集团有限公司，江西 南昌 330002；2. 华东交通大学土木建筑学院，江西 南昌 330013；3. 中南大学土木工程学院，湖南 长沙 410075；4. 南昌轨道交通集团有限公司，江西 南昌 330038)

在盾构隧道施工过程中，因盾构超挖作用、注浆不密实、浆液收缩，或运营中受地下水冲刷等多种因素耦合影响，地铁盾构隧道背后常伴有空洞存在[1−2]。空洞的存在导致该处地层抗力消失，衬砌受偏压作用，引起管片应力重分布，空洞边缘位置衬砌易出现应力集中效应，这可能导致管片产生开裂、破损掉块、渗漏水等病害[3]，在很大程度上降低了管片的安全性及耐久性。因此，分析和研究空洞缺陷对衬砌管片的安全性影响具有重要意义。目前，国内外对于衬砌结构背后空洞问题已经取得了一些成果，其主要采用理论分析、数值模拟、模型试验等手段。理论分析方面，主要针对隧道背后存在空洞建立相应围岩压力的修正计算方法及承载力损失率公式[4−5]。数值模拟方面，相关学者通过弹塑性有限单元法就衬砌背后存在空洞时隧道衬砌结构受力状态及开裂机制进行了相应研究[6−9]，认为空洞的存在恶化了衬砌结构力学特性，改变了衬砌结构的开裂机制，导致衬砌结构承载能力减小。模型试验作为一种常用的研究手段，能够很好地突出主要矛盾，准确把握现象的内在联系。闫高明等[10−11]针对隧道衬砌结构拱顶背后出现空洞开展大型振动台隧道模型试验，得出空洞显著降低了隧道结构的抗震性能，改变了隧道地震破坏模式，衬砌空洞处成为抗震薄弱部位；方勇等[12]就不同位置空洞与不同外水压荷载耦合作用下二次衬砌的受力分布规律及开裂特征进行研究；王士民等[13−14]针对隧道背后不同位置处空洞开展相似模型试验，认为拱肩位置空洞的存在更容易导致结构的失稳。上述研究中对象多为山岭隧道，针对地铁盾构隧道国内外研究较少，而地铁盾构隧道与山岭隧道变形及受力规律具有较大差异性。故本文以地铁盾构隧道为研究对象，采用模型试验手段，分别就管片背后不同位置处空洞衬砌变形及受力特征进行研究，为相关工程提供参考依据。

1 模型试验设计

1.1 模型试验仪器设备

本次试验中主要使用的仪器设备包括模型箱、水压表、土压力盒、百分表、应变片及动静态应变采集仪等，如图1所示。模型箱整体尺寸为3 000 mm×600 mm×2 000 mm(长×宽×高)，框架由镀锌方钢管、工字钢焊接而成，为清晰观察试验动态，框架四周采用12 mm 厚透明钢化玻璃，底板采用8 mm 厚的钢板承担上覆荷载；因模型箱高宽比较大，为防止倾覆等问题，于前后面板对称布置2道斜撑；考虑到试验过程中隧道放置、位移计安装、管线布置等问题，对前后2块钢化玻璃开孔，半径为350 mm。

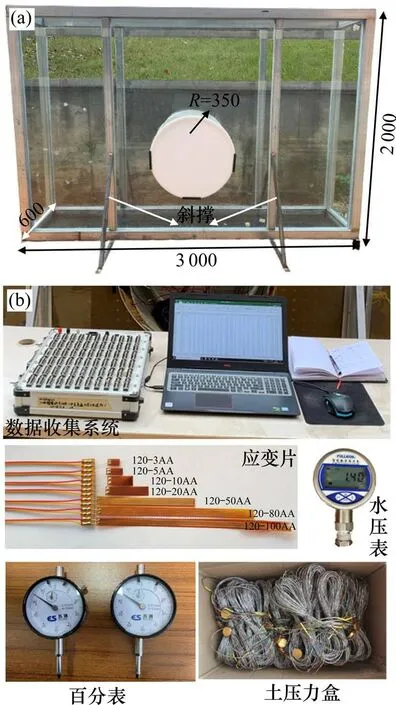
图1 模型试验系统Fig.1 Model test system

1.2 试验材料

本文以南昌地铁盾构隧道为依托，其中隧道外径6 200 mm，内径5 600 mm，环宽1 200 mm，隧道主要穿越地层为富水砂层及风化泥岩层，黏聚力较低，故采用过5 mm 筛的赣江河砂模拟土体。前期通过直剪、筛分、土粒比重及含水率试验[15]测定其基本物理力学参数如表1。

表1 土体物理力学参数Table 1 Physical and mechanical parameters of soil

确定原型与模型几何相似比为Cl=10，模型隧道采用4 环外径620 mm，环宽120 mm 钢圆环模拟，横断面不考虑管片环向接头，环间通过4对螺栓连接(图2(a))；对模型隧道进行对压试验[16]测定其圆环径向弯曲弹性模量为174.52 GPa(图2(b))。通过相似理论可知，衬砌结构主要以受弯为主，通过其弯曲受力、变形可判别其安全性，故将模型与原型等效抗弯刚度EI 模拟，最终控制其壁厚为8 mm。

图2 盾构隧道模型Fig.2 Shield tunnel model

试验前期在相应位置预设注满水的水囊，后期通过逐级泄压放水来模拟空洞的形成。为有效地获取管片的变形、受力规律，水囊尺寸取为250 mm×250 mm×150 mm(长×宽×高)，对应原型角度40°，深度1.5 m 空洞，水囊表面设注水口，前后面底部通过软管分别连接至止水阀及压力表，试验中通过压力表读数可精确逐级泄压放水，如图3所示。

图3 模型试验水囊Fig.3 Model test water bag

1.3 试验方案设计

试验共设置4 种工况，分别为无空洞、拱顶、拱腰、拱底背后空洞，通过改变水囊位置来实现，不考虑管片背后空洞尺寸的变化，规定管片拱顶处为0°，管片角度值随顺时针增长，如表2所示。

表2 试验工况表Table 2 Test condition table

因水囊注满水时即可视为管片无空洞工况，故试验只需进行3次，试验初始状态即为无空洞工况，当水囊放水泄压至压力表读数为零时，为试验最终状态。因水囊预设位置不同，虽水囊内压力一定，但上部所受土体荷载不同，故每次试验初始状态水压表读数也不尽相同；试验根据最大压力值，分3级进行均匀泄压，试验初始状态，各工况下压力表显示为18，24，30 kPa，故每隔6，8，10 kPa 进行分级放水，待其受力、变形稳定后收集试验数据。

量测对象选为中间2 环管片，前后2 环作为边界条件。量测内容包括：衬砌结构内力、变形位移、背后接触压力，如图4所示。结构内力通过在衬砌内外表面粘贴电阻应变片量测，每隔45°布置1 对；衬砌变形位移通过百分表量测，每隔90°布置，通过特制支架来测定管片绝对位移值(图4(b))；管片背后接触压力通过在衬砌外表面布置DMTY型应变式土压力盒量测，量程50 kPa，土压力盒每隔45°布置。

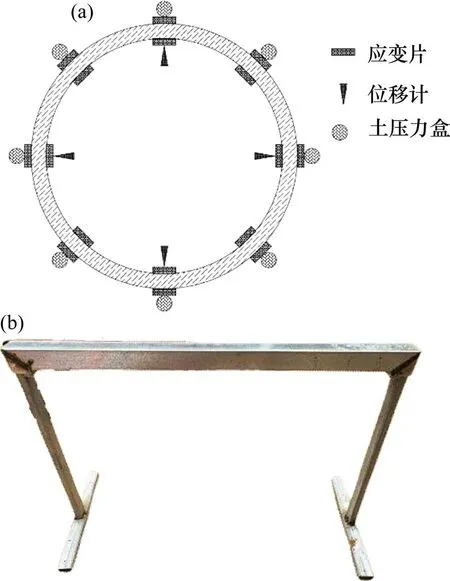
图4 监测点布设图Fig.4 Layout of monitoring points

根据应变片所测应变值可计算管片轴力及弯矩值，计算公式如下：

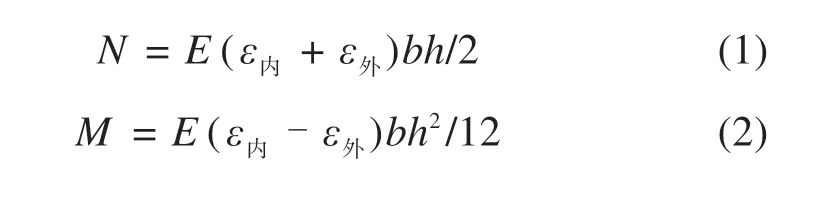
式中：E为衬砌弹性模量，ε内，ε外分别为衬砌内外表面应变值，b为截面宽度，h为衬砌厚度。

根据土压力盒所测应变值可计算管片背后接触压力值，计算公式如下：

式中：P为压力值；με为应变值；K为灵敏性系数。

2 试验结果分析

下文规定位移不区分正负，均为正值；轴力以受压为正，受拉为负；弯矩以衬砌外侧受压、内侧受拉时为正，反之为负。为更清晰表明管片受力及变形趋势，下文中管片变形、受力分布图均进行一定比例放大。

2.1 无空洞工况

无空洞时，管片内力呈“对称式”分布。轴力分布较为均匀，最大值出现在拱腰处(图5(a))；管片两侧拱腰处受负弯矩，拱顶、拱底处受正弯矩，45°，135°，225°，315°截面位置处附近均为反弯点，管片弯矩过渡较为平滑(图5(b))；衬砌管片所受地层压力较为均匀，管片拱底处接触压力较大，其他截面位置处接触压力差异较小，分布在20～25 kPa区间内(图5(c))。

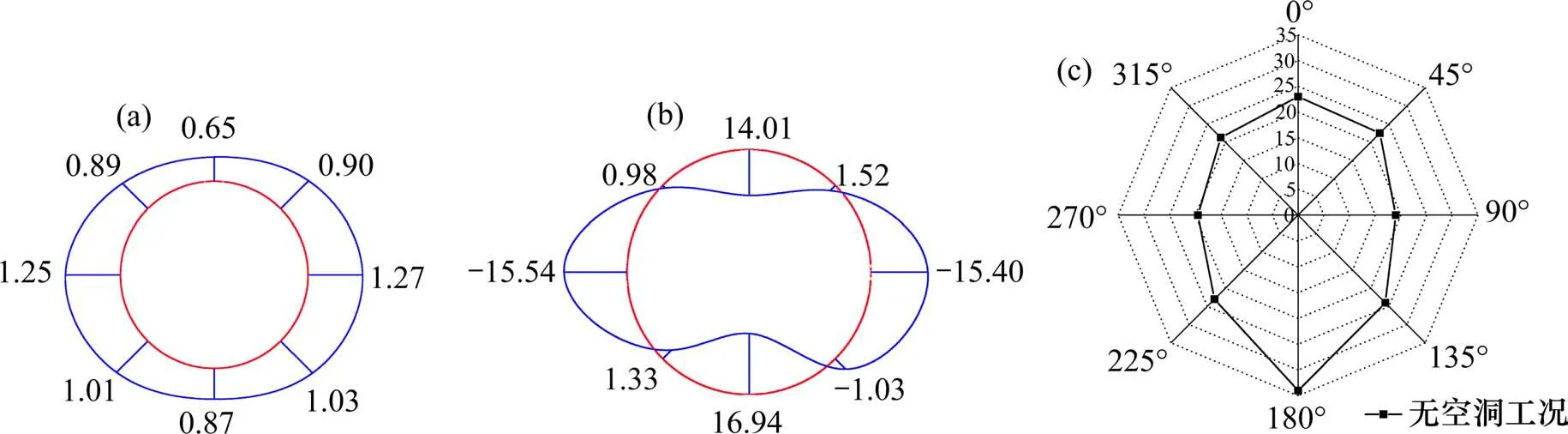
图5 无空洞工况管片内力、接触压力分布Fig.5 Distribution of internal force and contact pressure of segment in non-cavity conditions

总的来说，无空洞工况下，隧道与周边地层具有良好的接触状态，隧道管片受到均匀的地层压力作用，同时周边地层也提供管片充足的地层反力，管片轴力、弯矩分布都较为合理，过渡较为平滑自然。

2.2 管片拱顶背后空洞工况

空洞的形成导致管片拱顶及两侧截面处接触压力大幅度减小，P=0 kPa 时，最终空洞形成，水囊受重力作用掉落在拱顶处，拱顶接触压力值约为1.5 kPa，其他截面位置处管片接触压力也有一定减小，但幅度不大(图6(a))；拱顶处地层抗力消失导致该截面发生向上的变形位移，且随着压力值减小逐渐增大，最大位移值达2.24 mm，受地层水平压力作用，两侧拱腰处发生向圆心处变形位移，拱底基本处于固定状态，位移变化较小，隧道管片呈现“竖鸡蛋”式变形(图6(b)，图7(c))。

图6 拱顶背后空洞时管片位移、内力变化Fig.6 Displacement of segments and changes in internal force when the back of the vault is hollow

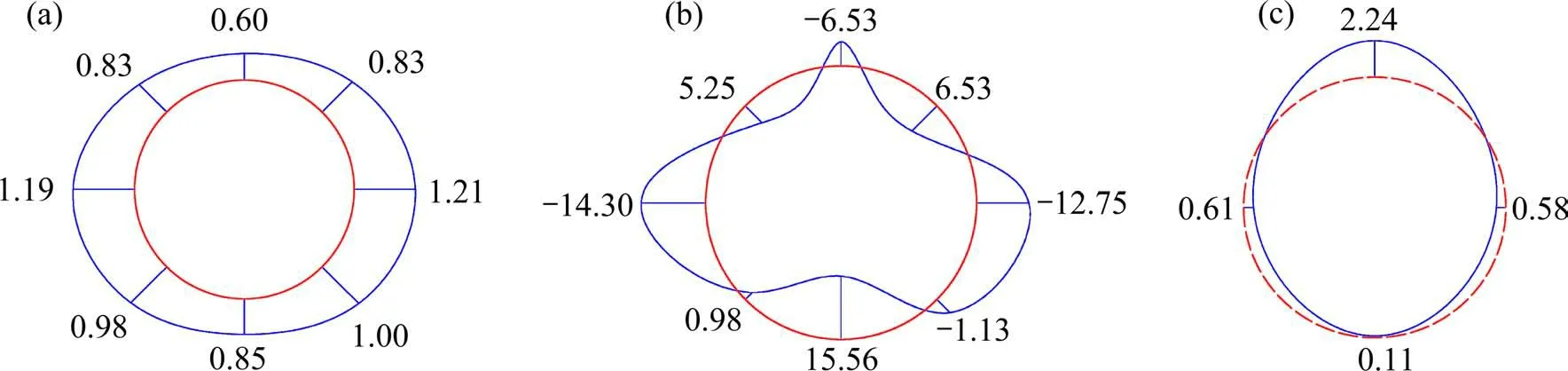
图7 拱顶背后空洞P=0 kPa时管片变形及内力分布Fig.7 Deformation of segment and internal force distribution when P=0 kPa behind the cavity of the vault

受拱顶卸载作用，管片各截面轴力均有所降低，其中拱顶处降幅最大，但整体降幅不明显，空洞的存在对管片轴力的影响较小(图6(c)，图7(a))；而对弯矩影响较大，拱顶背后空洞导致管片弯矩分布规律较无空洞时发生较大差异，P=6 kPa 时，拱顶弯矩值为2.99 N∙m，P=0 kPa 时，弯矩值为-6.53 N∙m，管片拱顶弯矩在P=0～6 kPa 之间发生反向，拱顶两侧出现反弯点，原45°，315°截面处反弯点均下移，拱顶由受正弯变为受负弯，管片外侧由受压变为受拉(图7(b))；拱顶弯矩值出现减小继而增大的变化趋势(仅考虑弯矩绝对值)，而两侧临近截面弯矩均有显著的增长，原拱顶弯矩值转由两侧截面来分担(图6(d))，空洞对应截面位置处管片弯矩变化率较大，过渡不平顺。

2.3 管片拱腰背后空洞工况

左拱腰(270°截面)背后空洞导致该截面接触压力最终值为0.5 kPa，这也进一步验证了该处空洞的形成；而管片左侧水平压力减小导致右拱腰(90°截面)处接触压力也随之减小，但减小幅度较左拱腰处稍小(图8(a))；同样，左拱腰处背后地层缺失导致该截面发生向空洞位置处水平位移，最大位移值达3.78 mm，拱顶处发生向下的协同变形位移，最大位移值为0.95 mm，管片整体呈现“横鸡蛋”式变形(图8(b)，图9(c))。

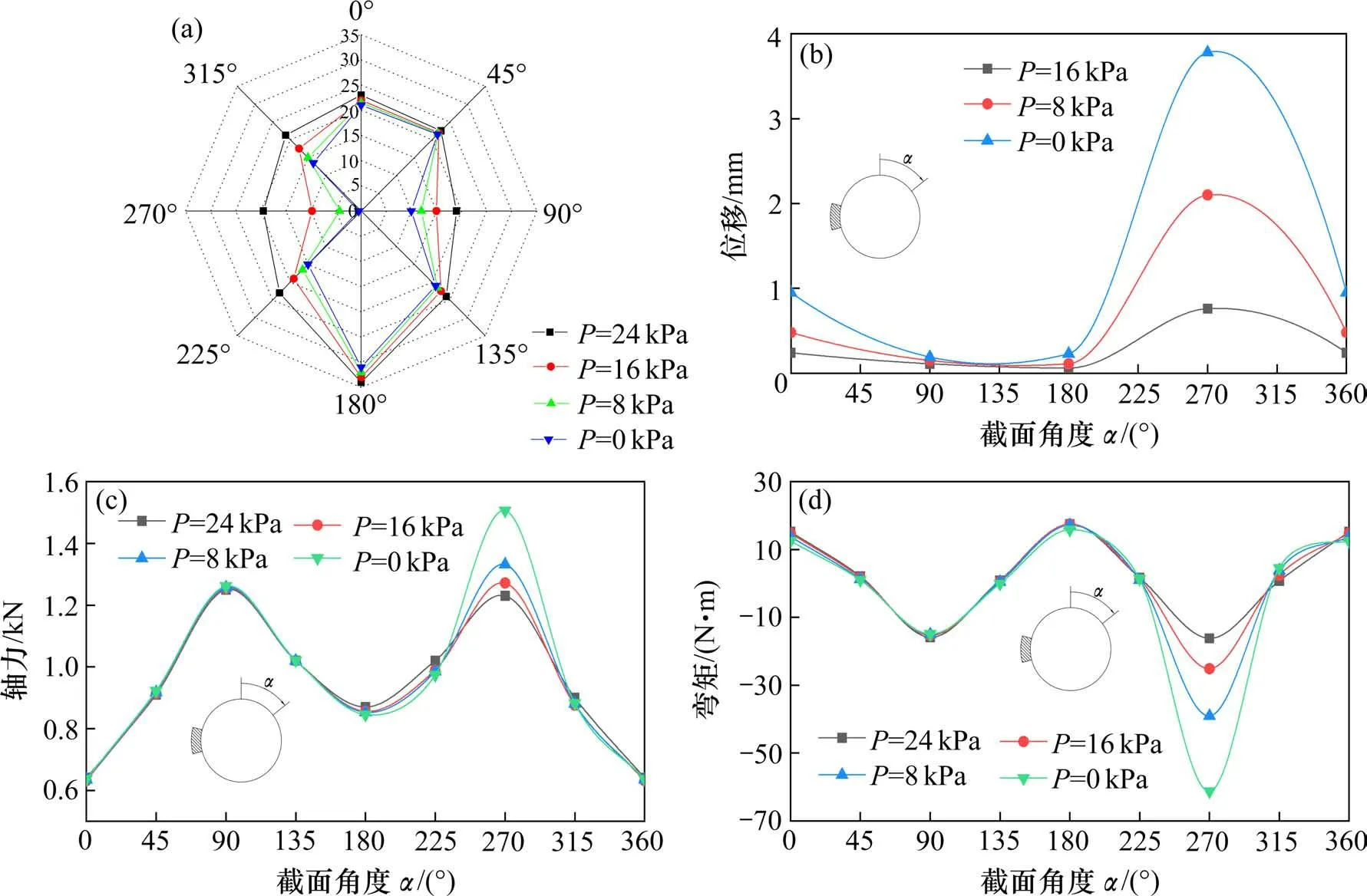
图8 拱腰背后空洞时管片位移、内力变化Fig.8 Displacement of segments and changes in internal force when the back of the arch waist is hollow

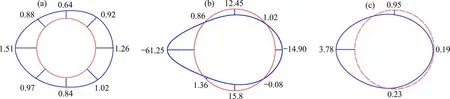
图9 拱腰背后空洞P=0 kPa时管片变形及内力分布Fig.9 Deformation of segment and internal force distribution when P=0 kPa behind the cavity of the arch waist

拱腰背后空洞导致管片该截面轴力值随压力值减小而逐渐增大，P=0 kPa时，轴力值为1.51 kPa，较无空洞时增长22.76%，轴力分布不均匀(图8(c)，图9(a))；与拱顶空洞不同，拱腰背后存在空洞时管片弯矩分布规律较无空洞时并未发生改变，而随着压力值减小，左拱腰处弯矩增长迅速，弯矩值呈“抛物线”式增长(图8(d))，P=0 kPa 时，弯矩为-61.25 N∙m，较无空洞时增加45.05 N∙m，增长约2.78 倍，管片外侧受较大拉应力易发生开裂等病害；管片弯矩分布倾向于空洞位置处(图9(c))，两侧拱腰弯矩呈不对称分布。

2.4 管片拱底背后空洞工况

管片拱底背后存在空洞时，隧道衬砌变形及受力趋势与拱顶背后空洞工况时均较为相似。

空洞导致拱底及两侧接触压力大幅度减小，P=0 kPa时，拱底接触压力约为0 kPa(图10(a))；同样，拱底处发生向下的变形位移，两侧拱腰处发生向圆心处变形位移(图10(b)，图11(c))；管片全周轴力值均出现降低，以拱顶处最为明显(图10(c)，图11(a))。

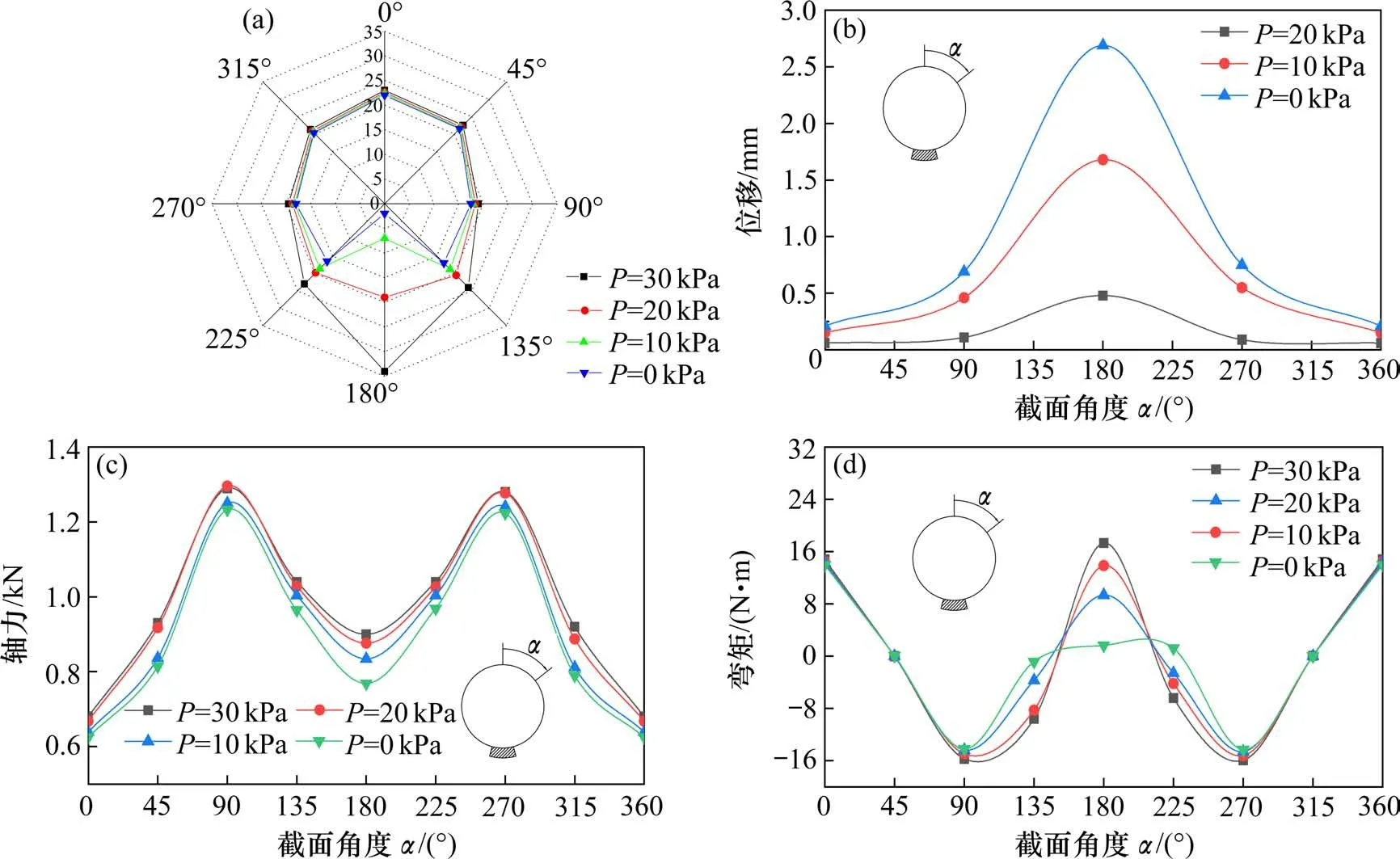
图10 拱底背后空洞时管片位移、内力变化Fig.10 Displacement of segments and changes in internal force when the back of the arch bottom is hollow

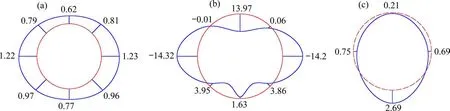
图11 拱底背后空洞P=0 kPa时管片变形及内力分布Fig.11 Deformation of segment and internal force distribution when P=0 kPa behind the cavity of the arch bottom

与拱顶背后空洞工况时弯矩变化规律不完全相同，拱底背后空洞时，该截面弯矩值逐渐减小，但并未出现反向，拱底依旧受正弯，P=0 kPa 时，拱底弯矩值为1.63 N∙m，弯矩接近于零，此时拱底处弯矩主要由两侧临近截面来承担，135°～180°及180°～225°截面处弯矩值有着显著的提高。

3 结论

1) 盾构隧道管片背后无空洞时，管片与周边地层具有良好的接触状态，衬砌受到均匀的地层压力，且周边地层也提供给衬砌充足的地层反力，管片内力呈“对称式”分布，且过渡较为平滑。

2) 空洞的存在改变了衬砌与周边地层的接触状态，衬砌受偏压作用，引起管片应力重分布，衬砌截面发生指向于空洞处的变形位移，衬砌结构整体受力状态恶化，内力分布较为复杂，空洞边缘位置处管片出现应力集中效应。

3) 管片背后不同位置空洞对隧道结构安全性影响的排序为：拱腰＞拱顶≥拱底。

4)拱腰背后空洞急剧增大了该截面处弯矩值，弯矩较无空洞时增长约2.78 倍，管片外侧受拉应力较大易发生开裂等病害；拱顶、拱底背后空洞工况，管片变形及受力趋势较为相似，空洞所在截面处管片弯矩值较无空洞均有显著降低，而两侧临近截面处弯矩值出现增长，原截面弯矩值转由两侧临近截面分担；不同的是，拱顶背后存在空洞时，该截面弯矩出现反向。