纯黏土地层锚杆加固隧道掌子面稳定性分析
2022-03-30熊小华刘安黄琦
熊小华,刘安,黄琦
(1. 江西交通咨询有限公司,江西 南昌 330038;2. 中南大学土木工程学院,湖南 长沙 410075)
盾构施工时,盾构机提供掌子面支护压力,确定合适的支护压力范围是保证掌子面稳定的关键;当隧道采用新意法开挖时,掌子面上并没有支护力,其稳定性通常采用安全系数的形式进行评价[1]。在实际工程中,锚杆加固是一种提高掌子面安全系数的有效方法[2−3],但其加固效果的定量计算还有待进一步研究。目前,国内外学者们采用数值模拟、离心机试验、解析方法等对有摩擦土地层中的锚杆加固掌子面进行了一定研究。数值模拟方面,PEILA[4]采用有限元方法研究了纵向玻璃纤维管加固掌子面问题,发现可以将加固效果等效为加在掌子面上的均布压力,因为这种加固效果似乎只取决于纤维管的数量,而不取决于土体属性;DIAS 等[5]采用均质法对锚杆加固掌子面进行三维数值分析,证明了均质法是水平锚杆加固设计的有效方法。实验方面,KAMATA等[6]通过模型试验发现,锚杆全长均有轴力且最大轴力位于锚杆中部,掌子面锚杆加固效果主要取决于轴向拉伸力;JUNEJA 等[7]通过离心模型试验研究了锚杆长度对掌子面稳定性的影响,发现锚杆加固可以改变掌子面前方的沉降槽形状,但不影响其宽度范围。解析方法方面,PINYOL 等[8]利用极限分析上限法研究了管棚加固下掌子面的稳定性,采用与竖向桩在水平荷载作用下响应相似的梁模型来考虑管棚与周围土体的相互作用;PAN 等[1]将“点生点”离散化技术推广到马蹄形截面隧道掌子面稳定性分析中,采用有限厚度区模拟锚杆−土体相互作用,再结合强度折减技术对锚杆加固掌子面的安全系数进行了评价。但是,以上研究对象均为有摩擦土地层,不适用于纯黏土地层。本文基于极限分析上限法理论,巧妙结合均质法和连续速度场概念,提出一种用于抗拉锚杆(纤维锚杆)加固下纯黏土地层隧道掌子面稳定性分析的三维模型,可为相关工况下的设计施工提供参考。
1 三维均质法考虑锚杆加固
根据以往研究,考虑锚杆加固土体的方法可以归结为两大类,即结构法和均质法。
结构法将锚杆剥离于土体单独分析,该方法常见于岩土工程分析的解析方法中,例如极限平衡法和极限分析法[9],且伴随着一些必要的合理假设,包括对岩土结构破坏模式的假定以及对于锚杆和周围土体之间相互作用的假设[10]。
均质法由BUHAN 等[11]提出,不同于结构法将土体与锚杆分开进行分析,该方法从宏观角度将锚杆加固下的土体视为具有各向异性的均质材料。
1.1 加固前土体应力状态分析
假设锚杆轴向与Z方向一致,在极限分析上限法的速度场中对土体进行应力分析,如图1 所示,加固前破坏机构内任意一点的应力可以用坐标张量表示为:
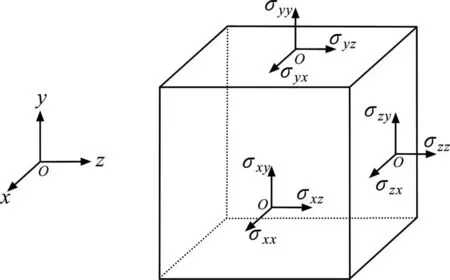
图1 加固前任意一点的应力状态Fig.1 Stress state at any point before reinforcement
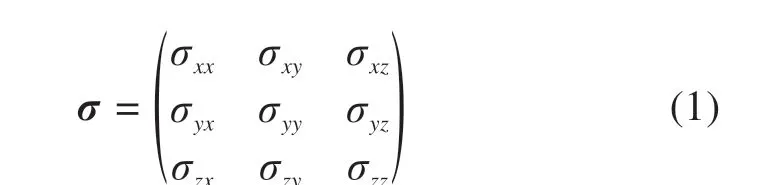
假设该点速度为v(vx,vy,vz),速度矢量与该点的Z轴正方向单位向量zi构成的平面记为πi,速度v的单位向量记为t,与速度v垂直的单位向量记为n,速度v与Z轴负方向的夹角记为Φ。首先计算单位向量t,其表达可以由正交坐标系下的速度坐标得到:
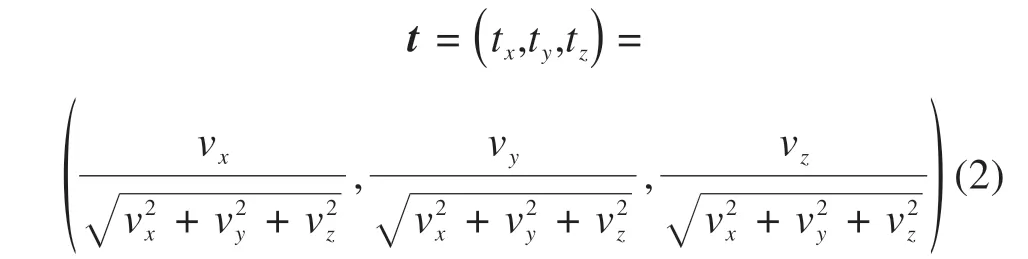
n=(nx,ny,nz)为法向量。分别根据单位向量的长度为1,n与v垂直、n与zi负方向夹角为“π/2−Φ”3个条件建立如下方程组:

此外,纯黏土服从Tresca准则,即破坏面上的切应力应等于黏聚力cu,即τt=cu。
1.2 加固后土体应力状态分析
锚杆加固后,将锚杆的抗拉作用叠加在土体内,土体视为均质的各向异性材料,此时加固区内任意一点的应力状态可用坐标张量表示为
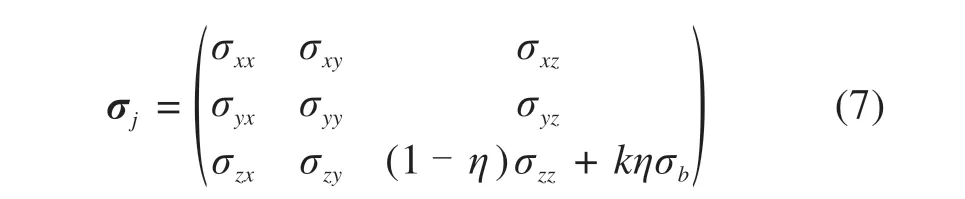
式中:k为范围系数,其值从−1 到1,用于表示锚杆的受力状态,−1表示锚杆处于受压破坏而1表示锚杆处于受拉破坏,玻璃纤维锚杆一般仅考虑受拉作用,因此k∈[0,1];η为锚杆在土体中的体积比,其值一般较小,数量级一般在10−2或10−3;σb为锚杆抗拉强度,远远大于土体的σzz,因此σzz的系数(1−η)可以近似为1,则式(7)近似为:

假设加固土体依然服从Tresca准则,则剪切应力τjt应该等于复合土体的黏聚力c′u,由此三维均质法下的加固土体黏聚力计算式为
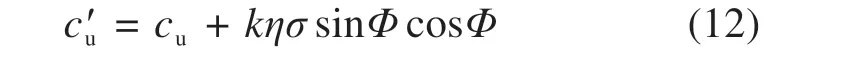
式中:kησbsinΦcosΦ部分即为锚杆加固作用下增加的黏聚力,其中Φ体现了黏聚力的各向异性,其值由式(5)确定。
1.3 三维均质法的改进
取任意一根锚杆进行细部分析,其横截面如图2所示,锚杆外围包裹一层注浆层,最外围才是土体。当锚杆加固机制发生失效时有4种不同的可能情形:1) 锚杆受拉屈服破坏;2) 锚杆与注浆层之间的胶结界面破坏;3) 注浆层与土体之间的胶结界面破坏;4) 端头上的锚板破坏。当其中任意一种破坏发生时,锚杆加固机制即失效,因此锚杆加固失效判定应以四者破坏中最容易发生的情况为标准,即为:
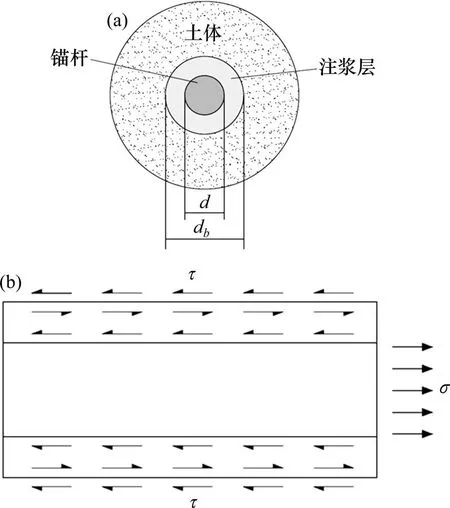
图2 锚杆示意图Fig.2 Schematic diagram of a bolt

式中:ri表示单根锚杆的抵抗作用;Ft为锚杆的抗拉强度;d和db分别表示锚杆和钻孔的直径;τm和τg分别表示锚杆−注浆层和注浆层−土体的黏结强度;a为锚杆的有效长度;Fp为锚板能够抵抗的最大拉力。
由于锚板一般只在停工期间才会安装,平时开挖状态下的锚杆是没有锚板的,因此可以不考虑;而锚杆−注浆层的黏结强度往往大于注浆层−土体的黏结强度,则式(13)可以简化为:
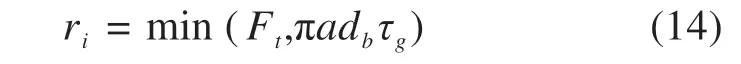
即锚杆加固作用的失效判定应为锚杆抗拉强度和注浆层−土体的黏结强度中的较小值,前文中的均质法只用锚杆抗拉强度σb考虑了锚杆的抗拉破坏,而实际上也可能发生注浆层−土体的黏结破坏,因此有必要对式(12)进行改进。
当发生锚杆抗拉强度破坏时,锚杆抗拉强度σb为:
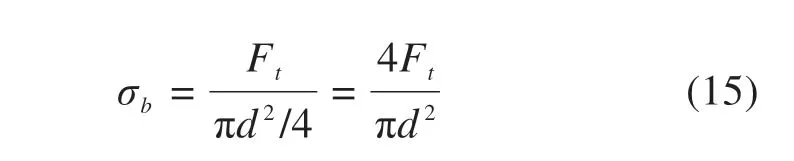
为了保持式(12)的一致性,当发生注浆层−土体的黏结破坏时,依然取单位长度锚杆(a=1)转化为等效的锚杆抗拉强度σb表示,此时σb为:
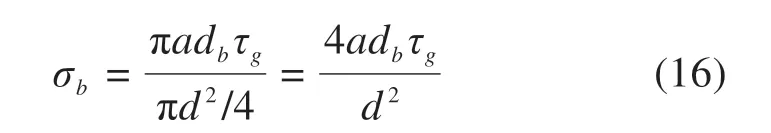
结合式(14),则式(12)中的σb应为:
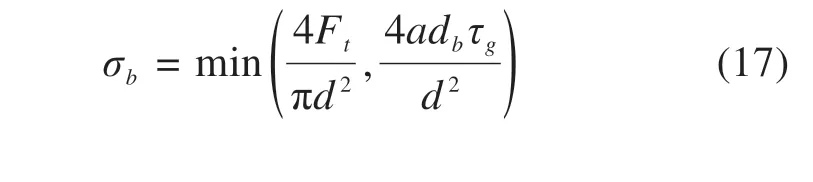
2 考虑锚杆加固的纯黏土隧道掌子面稳定性分析
2.1 掌子面稳定性三维能耗分析
为了准确评估纯黏土地层隧道掌子面稳定性,MOLLON 等[12]根据SCHOFIELD[13]的离心机实验现象,结合数值模拟结果,提出了比以往模型更优的三维连续速度场破坏模型,为众多学者采纳和推崇。为了避免复杂积分,MOLLON 等[10]还将模型离散化,化积分运算为求和运算,详细推导过程可参照其原文。
连续速度场较为复杂,难以采用传统的结构法分析锚杆加固。本节根据极限分析上限定理,将改进的三维均质法应用于MOLLON 等[12]提出的三维连续速度场中,通过外力做功功率等于内部能量耗散率建立能耗方程,分析锚杆加固下的纯黏土隧道掌子面稳定性,三维破坏机制及相关参数如图3,总体能耗方程为:
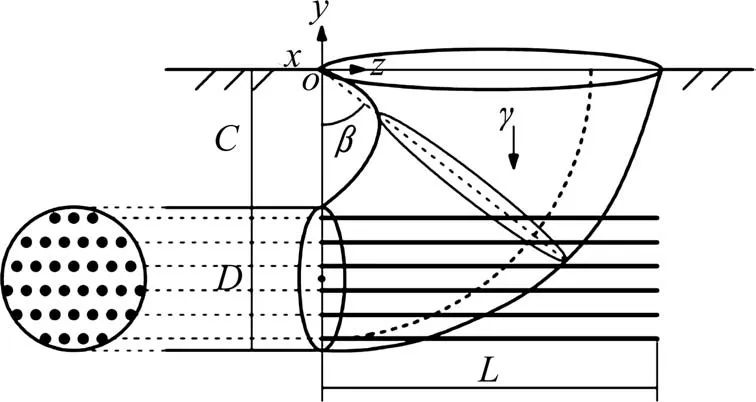
图3 破坏机制示意图Fig.3 Schematic diagram of failure mechanism
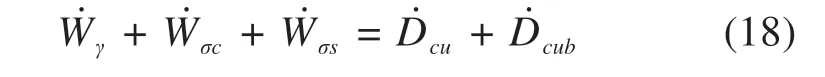
式中:Ẇγ为土体自重的功率;Ẇσc为隧道掌子面支护压力的功率;Ẇσs为地表荷载的功率;Ḋcu为非锚杆加固区的内部能量耗散率;Ḋcub为锚杆加固区的内部能量耗散率。
将模型离散化后,式(18)中的每一项可用离散单元的求和形式给出,具体计算表达式如下:
1)土体自重做功功率
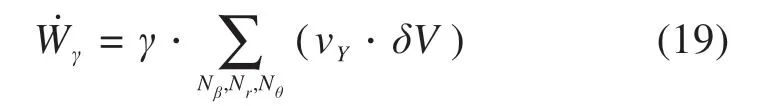
2)掌子面支护压力做功功率

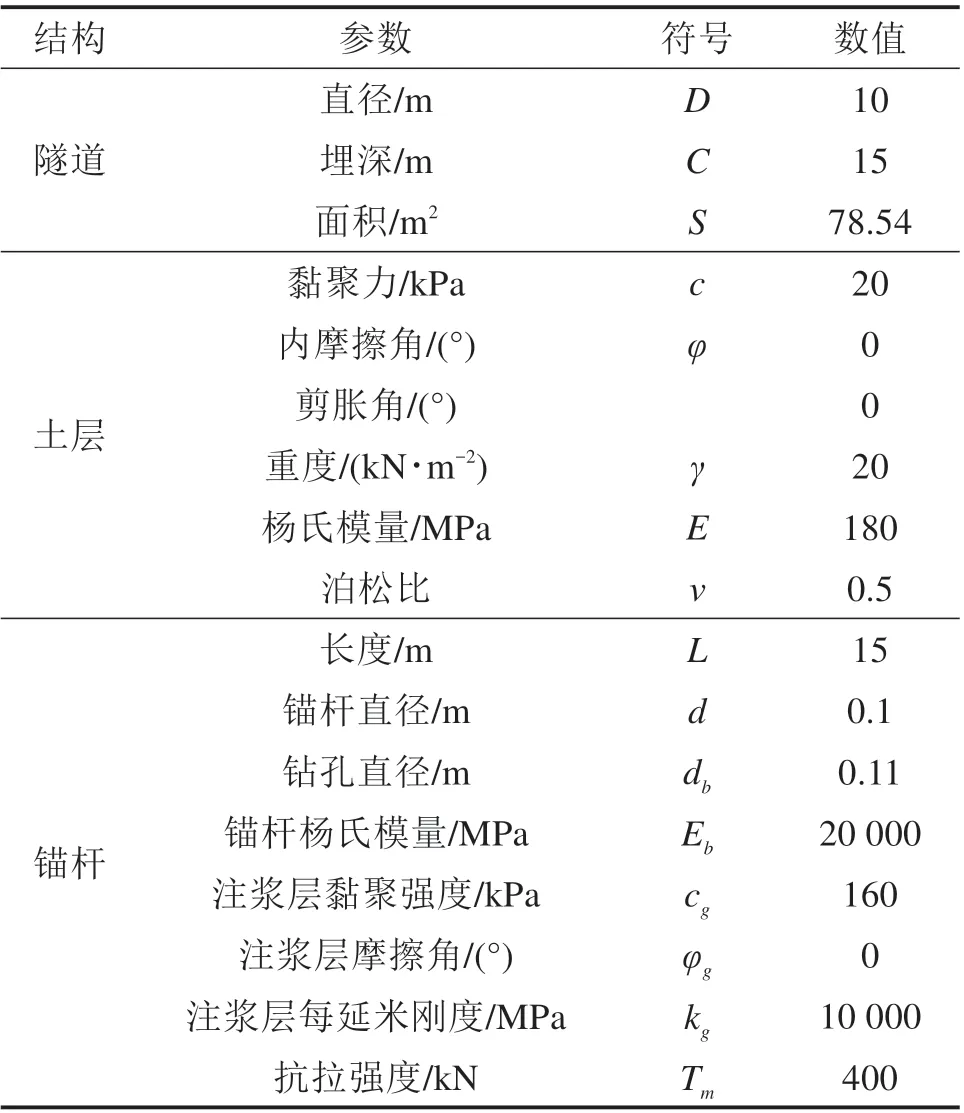
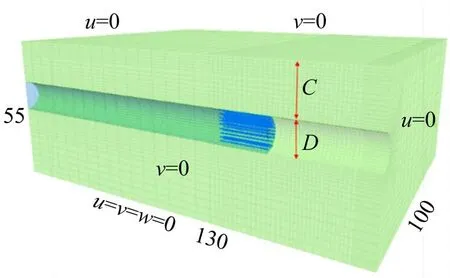
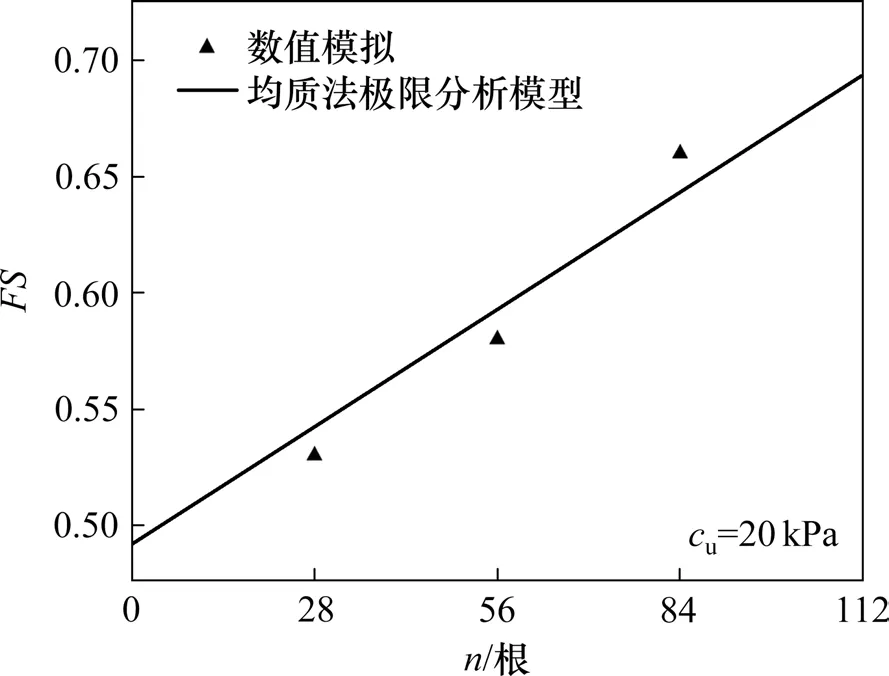
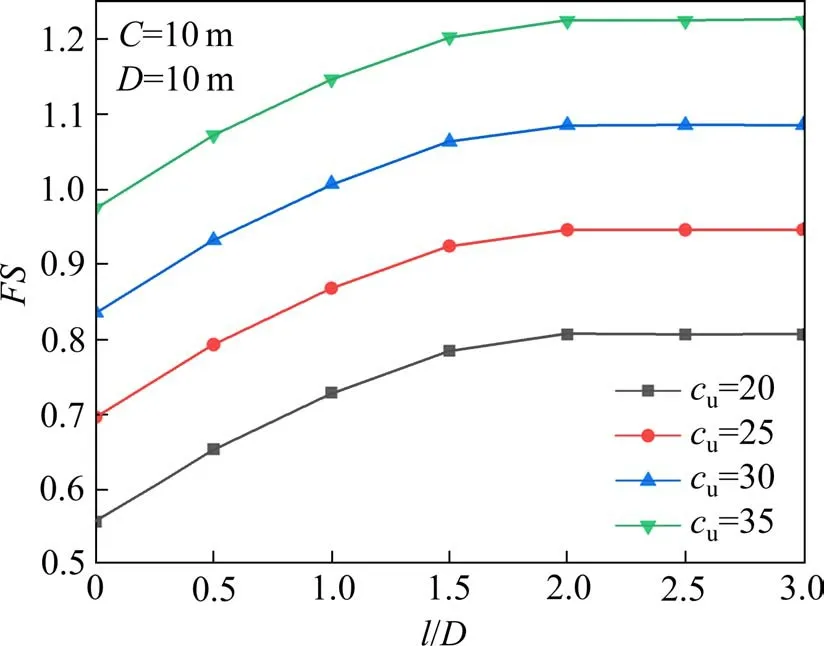
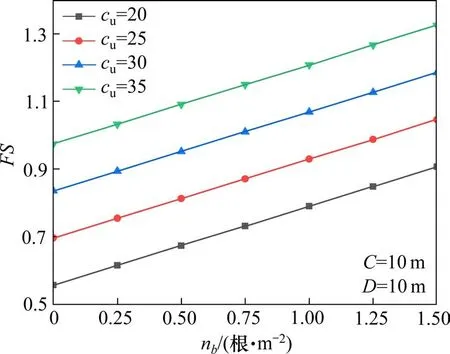
加固区域为: {0 以上式中:σc表示施加在隧道掌子面上的均布极限支护压力;cu表示土体本身的不排水黏聚强度;c′u表示加固区土体的等效黏聚强度,其值由式(12)和式(17)确定。 将式(19)~(23)代入式(18)中,解得隧道掌子面极限支护压力为: 为了便于理解,将上式简化,则坍塌破坏极限支护压力计算式为: 式中:Nγ,Ns,Nc和N′c分别为表征土体自重、地表荷载、土体强度、锚杆加固作用4个影响因素的无量纲参数,其计算表达式如下: 由此,锚杆加固下的掌子面坍塌破坏极限支护压力可以求得。值得注意的是,在坍塌破坏情况下,隧道掌子面上支护压力作用方向与速度方向相反,根据极限分析上限法原理,得到的极限支护压力实际上是真实极限的一个严格下限解。 在采用新意法开挖的隧道中,掌子面上实际并不存在均布压力用以抵抗前方土体的坍塌趋势,因此采用安全系数评价掌子面稳定性更为合理。根据以往文献,一般有2种方法定义和计算安全系数,其中一种定义安全系数为内部抵抗作用和外部荷载作用的比值,比如在极限分析中的内部总耗散率和外部总功率之比可以视为安全系数;另外一种方法为强度折减法,以黏聚力和内摩擦角的数值折减为特点,该法在Mohr-Coulomb 材料中使用广泛。PAN 等[1]对比了2 种方法在极限分析中得到的结果,发现后一种方法比前一种方法更保守,偏于安全,因此本文采用强度折减法计算安全系数。 在强度折减法中,黏聚力c和内摩擦角φ同时以同一系数FS折减,折减后的值为: 在折减后的黏聚力cF和内摩擦角φF条件下,当掌子面上所需的极限支护压力为0 时(亦即外力做功功率等于内部能量耗散率),折减系数FS即为安全系数。由于纯黏土服从Tresca法则,内摩擦角为0,仅有不排水黏聚力cu,所以仅需对一个参数进行折减,即: 将式(31)嵌入至前述三维能耗方程中,在极限支护压力σc为0 时解方程中的FS即得到安全系数。为了得到较为精确的安全系数,此处采用二分法来实现计算过程。 为了验证本文方法的正确性,建立数值模型对比验证。数值模拟采用三维有限差分软件FLAC3D完成,该软件广泛用于岩土结构的科研和应用。数值模型涉及的具体相关参数见表1。 表1 数值模拟模型的基本参数Table 1 Parameters of numerical simulation model 根据表1 的参数建立直径10 m 埋深15 m 的三维隧道开挖模型,如图4。 图4 数值模拟模型图Fig.4 Numerical simulation model 整个模型沿开挖方向长130 m,横向100 m,高55 m。边界条件设置方面,底部边界完全固定,其余四周边界法向固定,顶部为自由边界。 采用该数值模型计算安全系数时同样采用的是强度折减法结合二分法,计算精度为0.001,计算结果对比见图5,其中极限分析模型所采用参数与数值模拟参数一致。 从图5 中可以看出,当cu=20 kPa 时,本文提出的均质法极限分析模型得到的结果与数值模拟结果趋势一致,数值相近,最大差异为布置84 根锚杆时,两者此时也只相差2.5%。 图5 数值对比Fig.5 Numerical comparison 基于验证过的极限分析模型,分析不同锚杆长度和锚杆布置密度对纯黏土隧道掌子面稳定性安全系数的影响。 图6 显示了不同黏聚强度cu下无量纲参数L/D和安全系数FS的关系。采用的相关参数如下:D=10 m,C=10 m,L/D=0~3.0,n=84 根,d=0.1 m,db=0.11 m,cg=160 kPa,Tm=400 kN,γ=20 kN/m3,cu=20~35 kPa,σs=0。 从图6中可以看出,掌子面安全系数首先随着锚杆长度的增加而增加,然后趋于平缓,最终稳定于某个值。不同埋深下达到最终值的锚杆长度也不同,埋深10 m 下的锚杆最大有效长度为20 m,即为隧道埋深和直径之和(C+D)。在以往文献中,贺祚等[14−15]对c-φ土隧道掌子面锚杆加固进行过详细的研究,最优锚杆长度常常用隧道直径D的倍数表示。因为c-φ土存在“拱效应”,其加固锚杆的最优长度与埋深无关,仅与隧道直径有关,而在本文模型中,浅埋纯黏土隧道的加固锚杆最优长度与埋深和直径均相关,为C+D。 图6 锚杆长度对安全系数的影响Fig.6 Effect of bolt length on safety factor 图7 显示了不同黏聚强度cu下锚杆密度nb和安全系数FS的关系。为了保证锚杆均有效,采用的锚杆长度为L=C+D,其他相关参数如下:D=10 m,C=10 m,nb=0~1.5 根/m2,d=0.1 m,db=0.11 m,cg=160 kPa,Tm=400 kN,γ=20 kN/m3,cu=20~35 kPa,σs=0。 图7 锚杆密度对安全系数的影响Fig.7 Effect of bolt density on safety factor 从图7中可以得知,安全系数随着锚杆密度的增加而线性增大。当埋深C=10 m 且cu=35 kPa 时,没有锚杆加固下的安全系数FS为0.97,而锚杆密度为1.50 根/m2布置时的安全系数FS为1.32,锚杆的加固作用使得掌子面从不稳定变为稳定状态;当cu=20 kPa 时,没有锚杆加固下的安全系数FS为0.56,而锚杆密度为1.50 根/m2布置时的安全系数FS为0.89,掌子面依然处于非稳定状态,且此时锚杆布置已经非常密集,继续加大锚杆密度很不经济。因此,当埋深较大且土质较差时,仅有锚杆加固是不够的,应配合其他加固措施以综合提高掌子面的稳定性,比如联合采用管棚加固或者地表注浆加固等。 1) 浅埋隧道中,纯黏土地层下的锚杆最优长度与隧道直径、覆土埋深均相关,在本文模型中近似为两者之和(C+D),最优长度的具体值需通过实验进一步验证。 2) 纯黏土地层采用受拉锚杆加固效果不是特别显著,当埋深较大或黏聚强度较小时,纯黏土隧道掌子面仅采用抗拉锚杆加固是欠安全的,应该与其他加固措施(如管棚加固、地表注浆等)相结合。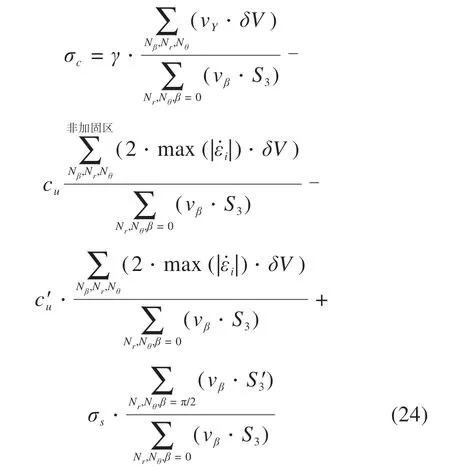
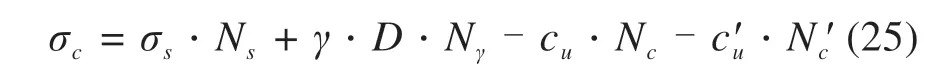
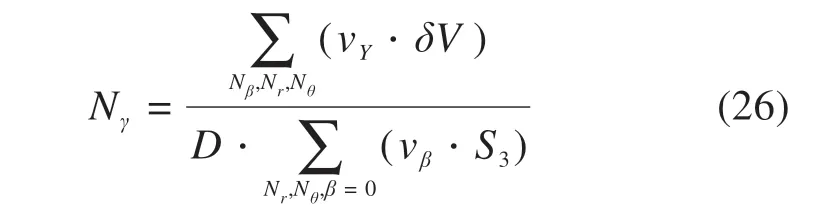
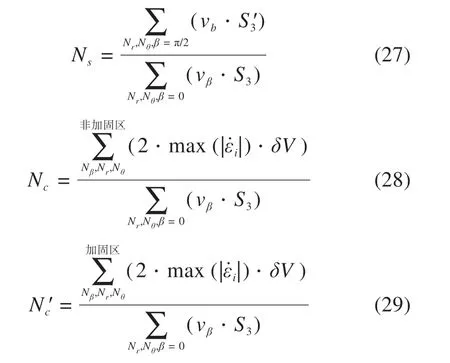
2.2 安全系数计算
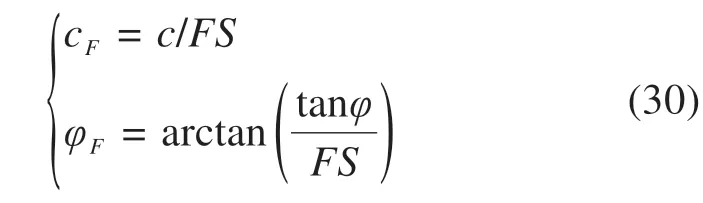

3 模型验证
4 参数分析
4.1 锚杆长度L的影响
4.2 锚杆密度nb的影响
5 结论
