蜂窝芯体高速冲击性能研究

2022-03-30雷彬姚松胡捷

铁道科学与工程学报 2022年2期

雷彬，姚松，胡捷

(中南大学交通运输工程学院，轨道交通安全教育部重点实验室，湖南长沙 410075)

蜂窝结构由于其低密度，高比刚度，变形可控和成熟的制造工艺，在被动安全保护等工程应用领域得到了广泛应用[1−2]。基于此，学者们对蜂窝进行了大量研究来探究其压缩[3]，弯曲[4]和疲劳[5]等整体受载性能。近年来，随着交通工具运营速度的提高，蜂窝承受高速冲击时的局部受载性能也在工程应用中越来越受到重视。其中，SUN 等[6]对单一蜂窝三明治结构进行了试验和仿真研究，并研究了夹芯板几何参数对穿透过程的影响。BU‐ITRAGO 等[7]分析了复合材料蜂窝夹芯板在高速冲击下的穿孔过程，并对面板和蜂窝芯体的损伤机理进行了分析。FELI等[8]研究了弹体在高速穿透蜂窝状夹层结构时各结构对冲击过程和整体能量吸收能力的影响。ZHANG 等[9]为了研究蜂窝夹层结构对子弹和碎片的防护作用，对蜂窝夹层结构进行了弹道冲击研究，分析了蜂窝结构自身因素对高速冲击过程的影响。张旭红等[10]对铝蜂窝夹芯板承受爆炸载荷时的动态冲击响应进行了研究，并分析了蜂窝的几何尺寸、板厚等因素对夹芯板的变形和失效模式的影响。廖高健等[11]采用轻质多孔火山岩冲击物模拟太空碎片对蜂窝夹层板进行了超高速撞击试验，对蜂窝夹层板的损伤特性进行了分析，发现在超高速冲击下，蜂窝夹层板的损伤模式主要包括上表面蒙皮穿孔、蜂窝坍塌和脱胶等损伤模式。尽管这些研究已经对蜂窝的高速冲击性能进行了分析，但大多数都是关注于蜂窝夹芯结构而不是蜂窝芯体本身，而且，这些研究基本是对完全穿透时的蜂窝性能进行分析。但是，在一些工程应用中，却会出现一些不同的情况。例如，在中国新一代磁悬浮列车的被动安全保护中，以蜂窝为主吸收异物高速冲击的能量，同时为了保护后方设备与列车司机，严格禁止蜂窝被完全穿透的情况发生。因此，在新一代高速磁浮列车的设计研发过程中，蜂窝被异物冲击时的侵入深度和损伤情况受到很大关注。在本文中，使用高速冲击系统进行了3 种不同速度的冲击试验，获得了蜂窝芯体内部形变和冲击弹丸的侵入深度。然后，ABAQUS 中建立了有限元模型，并根据试验数据对该模型进行了校验。最后，结合试验与仿真结果对蜂窝的弹体侵入深度和变形模式进行了分析。

1 蜂窝高速冲击试验

1.1 试件准备

试验试件由蜂窝芯体，底板和保护壳3个部件组成。其中，蜂窝芯体材料为铝合金(AA3018-H18)，底板与保护壳材料为钢(Q235)，蜂窝芯体和保护壳使用环氧树脂粘接在底板上。蜂窝芯体胞元为正六边形，胞壁厚度t和胞元尺寸l分别为0.08 mm 和2 mm。蜂窝芯体的外形尺寸为400 mm(长)×400 mm(宽)×600 mm(厚)mm。蜂窝和其孔格结构及参数示意图见图1。其中，保护壳仅用来防止蜂窝芯体在运输过程中损坏，且未与蜂窝芯体直接接触(与蜂窝距离约5 mm)，同时，蜂窝承受高速冲击时发生局部形变，边界对冲击过程的影响极小[7]。因此，在本文中忽略了保护壳对冲击过程的影响。

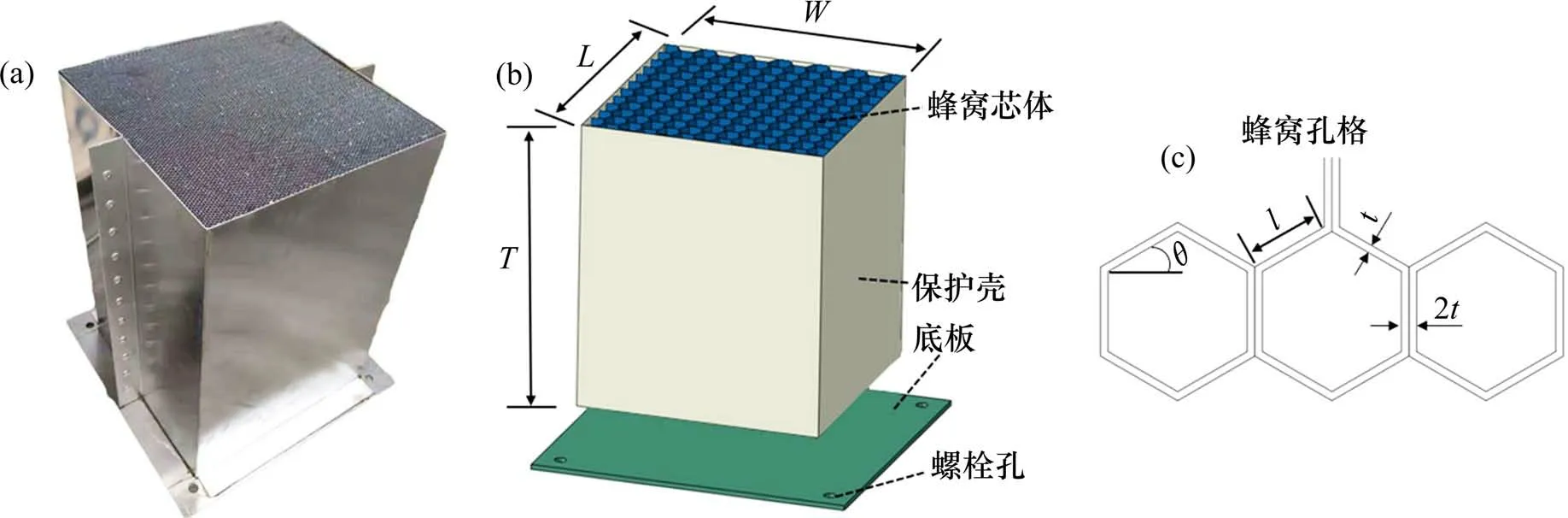
图1 蜂窝试件及其部件Fig.1 Honeycomb specimen and its components

1.2 试验过程

使用车辆部件冲击系统(见图2(a))进行高速冲击试验，该装置使用压缩空气驱动冲击弹丸。当空气罐中达到预设压力时，压缩空气被释放并推动冲击弹丸在加速炮管中加速。冲击弹丸外形如图2(b)所示，其总重量为972 g，总长度为103 mm。试验发现，弹丸基本无可见形变，因此，弹丸在3次冲击过程中重复使用。在防护罩的侧面，布置有高速摄像设备(图中未显示)，用来计算弹丸的实际冲击速度。通过调节压缩空气的压强，可以使弹丸获得不同的冲击速度。在本次试验中，冲击3个试件的弹丸实际冲击速度分别为394，507 和627 km/h。每次冲击过程结束后，对试件进行切割，取出冲击弹丸并测量弹丸的侵入深度，并获得蜂窝的内部变形情况。

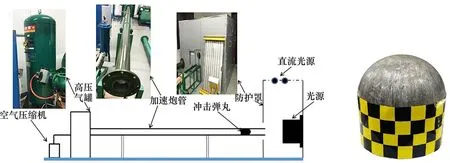
图2 试验装置Fig.2 Test equipment

2 蜂窝高速冲击有限元仿真

2.1 有限元模型的建立

使用Abaqus/Explicit 建立了有限元模型。该有限元模型由蜂窝芯体，冲击弹丸和底板组成，试验中其他工装则以边界条件的形式给出。考虑到约束条件和模型结构的对称性，同时为了提高计算效率，实际建立的是蜂窝、底板和弹丸的1/4 模型，如图3 所示。蜂窝芯体采用壳单元(S4R)进行划分，网格大致尺寸为1 mm，并在冲击中心区域(约80 mm×80 mm)进行了局部加密；冲击弹丸及底板采用六面体网格进行划分，网格尺寸分别为5 mm 和20 mm。根据上述试验和类似文献中的发现[6,12]，形变量十分微小的冲击弹丸可以视为刚体，因此，此处对冲击弹丸施加了刚体约束。此外，使用“tie”约束模拟蜂窝芯体和底板的连接，使用“hard contact”定义法向接触关系，并使用“Static-Kinetic Exponential Decay”定义切向接触。

图3 1/4有限元模型Fig.3 FE model of impact system

对于高速冲击这类大变形问题，材料的应变率效应明显，合适的材料本构对仿真结果的准确性有重要影响[13]。Johnson-Cook 模型通常用于模拟变形较大的情况，并对应变率效应导致的材料硬化进行了考虑。Abaqus用户手册中给出的J-C本构模型定义如下：

其中：σ是von Mises 等效应力，4 个参数A，B，n，C是通过试验测得的材料常数[14]。SUN等[6]通过试验给出了铝合金AA3003-H18 的Johnson-Cook 参数的详细数据(表1)。同时，在本文中使用“shear damage”定义蜂窝芯体单元的失效，文献[15]通过试验和数值仿真对该失效应变值进行了校准，发现该值为0.4 时能很好地模拟该速度范围下的蜂窝芯体形变过程。表2列出了有限元模型中各部件的基本材料参数，其中，弹丸的密度根据实际质量和体积进行了调整，使得有限元模型中弹丸的质量为实际质量(972 g)的1/4。

表1 蜂窝芯体材料的J-C参数Table 1 Parameters of Johnson-cook model

表2 试件各部件基本材料参数Table 2 Basic mechanical properties of different parts of the FE model

2.2 有限元模型验证

为了验证有限元模型的准确性，将上述试验情况与有限元计算结果进行对比。

在本文的每次冲击试验中，弹丸的动能始终不足以穿透整个蜂窝芯体，因此，弹丸在蜂窝内部的侵入深度是一个可行的对比指标。将弹丸在蜂窝内行进的最远距离定义为侵入深度。当冲击过程完成后，切割蜂窝并测量得到弹丸的侵入深度。这里，比较2 种不同冲击速度下(394 km/h 和627 km/h)的弹丸侵入深度(时速507 km/h 的情形将在后续进行讨论)。表3给出了2种速度下的试验结果与有限元结果的侵入深度数据，显然，仿真结果与试验结果十分接近，其中，时速627 km/h 时两者误差稍大，但仍在3.14%以内。

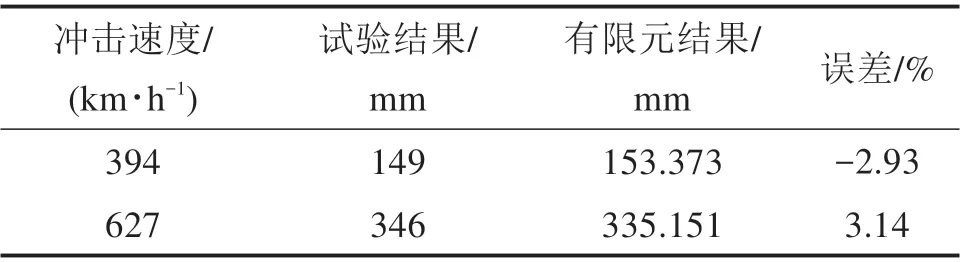
表3 侵入深度对比Table 3 Comparison of penetration depth

然后，对2 种结果中的蜂窝变形情况进行对比。图4为有限元仿真与试验中试件的俯视图。在图4(a)中，冲击中心区域的网格由于变形过大已被删除，形成了明显的弹坑。由于冲击弹丸的侧向挤压，在弹坑边缘有3～4 层铝箔堆叠在一起，形成了较为明显的弹坑内壁。在弹坑边缘的附近，还有2～3 个胞元存在肉眼可见形变。在离弹坑更远的区域则观察不到明显变形。这与图4(b)所示的试验结果是非常吻合的。对2种试验中弹坑外表面开口直径进行了对比，结果发现有限元结果中(106 mm)弹坑开口与试验结果(108 mm)较为相近。图4(c)显示了蜂窝内部损伤情况，在弹坑的内壁上，附着有少量弯曲的片状铝箔，由于弹丸挤压，弹坑的内壁都显得较为平滑。这也与试验结果(图4(d))吻合得较好。

图4 蜂窝损伤情况Fig.4 Honeycomb failure

以上对比表明，仿真结果能够很好地还原试验结果，即该有限元模型能准确有效地对该高速冲击过程进行模拟。

3 结果与讨论

在上述经过验证的有限元模型基础上，共进行了不同冲击速度的7次仿真计算，速度分布如表4所示。

表4 各试算速度Table 4 Impact velocity of each test

3.1 侵入深度

侵入深度是工程领域用以评价蜂窝可靠性的重要指标，工程领域尤其关注特定速度区间内弹丸侵入深度的变化规律。考虑到有限元结果与测试结果之间的误差较小，此处在有限元计算结果基础上讨论侵入深度的变化规律。

比较直观的是，弹丸冲击速度的增加会增加初始动能，从而使侵入深度有增加的趋势。但是，冲击速度的增加还会导致材料的硬化等因素。因此，需要进一步分析才能得到侵入深度的变化规律。将上述7 个算例的侵入深度数据绘于图5 中，并使用多项式对这些数据进行拟合，拟合得到的方程和曲线也在图中给出。

图5 不同速度时的弹丸侵入深度Fig.5 Penetration depth under different impact velocities

可以看到，当使用二次多项式进行拟合时，侵入深度的各数据点很好地分布在拟合的拟合曲线上，相关系数R2非常接近1，这表明拟合结果的精确度是较高的。因此，在200～700 km/h 的速度范围内，冲击弹丸在蜂窝内部的侵入深度变化可最低使用二次多项式进行拟合，且能获得较好精度。这可为工程应用提供一定的参考。

3.2 损伤模式

蜂窝在高速冲击下的损伤模式在实际应用场景中至关重要。总体而言，由弹丸冲击引起的蜂窝损伤包括铝箔的弯曲、断裂和胶黏失效导致的剥离。此处，将损伤分为2类：可以从试件外部直接观察到的外部损伤；在切割样品后才易于观察的内部损伤。

1) 外部损伤

除了在上一节中讨论的外部变形之外，还能从顶部视图中发现试件存在局部胶黏失效。由于过大的局部应力，在每个样品中都存在如图6(a)所示的局部开裂。在试件表面，局部裂纹基本分布在弹坑两侧的少数几个孔格处，随后的观察表明，在试件的内部同样存在着局部裂纹。

图6(b)为本次试验中损伤情况最严重的试件，对该试件进行冲击的弹丸初速度为507 km/h(140.8 m/s)。在该试件中，外表面出现了由上至下的整体裂纹，后续处理结果表明，裂纹从蜂窝芯体的表面延伸到了接近底板的位置，导致整个试样出现了开裂。因此，在上一章节未将该试件数据用来校验有限元模型，后续测量数据也表明，该样品的侵入深度达到287 mm，比有限元计算结果(237.55 mm)高出20.8%，侵入深度的不合理提升意味着蜂窝芯体的胶黏强度对其受高速冲击时的性能表现有着重要影响。

图6 胶黏失效导致的开裂Fig.6 Cracking caused by adhesive failure

2) 内部损伤

使用切割装置切开蜂窝获得了内部的损伤情况。从图7可知，冲击中心区域已经完全塌陷形成了一个弹坑，在弹坑的内壁上有一些半脱落的铝箔被挤压成片状，而远离弹坑的区域变形逐渐减小，直至几乎无明显形变(图7(a)和图7(b))，这与外部变形情况是吻合的。在弹坑的底部，有一小部分脱落的被高度挤压折叠的铝箔。在弹坑下方10 cm 左右，仍然能发现已经弯曲的铝箔。此外，还获得了弹坑下方区域的内部损伤情况。蜂窝芯体和底板保持了良好的垂直连接，这得益于良好的黏合性能。对弹坑下方无可见形变区域进行了切割，获得了从7(c)所示的图像，可以看到，图中存在着明显局部开裂，这说明无可见形变区域在承受冲击时也存在着较大的局部应力。