钢箱组合梁桥施工过程受力性能影响因素分析

迟敬来

摘要 为研究钢箱组合梁桥施工过程对桥梁弯扭稳定性的影响程度，以某匝道接线桥为依托，选取施工过程荷载、波形顶板厚度、施工顺序、箱梁初始几何缺陷作为基本影响因素，利用abaqus构建精细化有限元模型，针对这些因素对简支梁弯扭稳定性的影响规律进行了分析。分析表明：波纹钢顶板厚的增大能在一定程度上提高箱梁的抗扭刚度，合理的施工顺序能改善其动力性能，减小施工期间屈曲失稳的风险。

关键词 屈曲模式;有限元分析;初始缺陷;薄壁结构;弯扭稳定性

中图分类号 TP3 文献标识码 A 文章编号 2096-8949（2022）05-0150-04

0 引言

钢箱-混凝土组合梁桥能够节省材料，还可以简化施工工序，具有经济性突出和利于工业化建造等优点[1-3]。

钢箱梁的截面由钢腹板和底板及较小的翼缘顶板组成，属于开口钢箱。该类结构的缺点是，在施工期间，桥面板混凝土达到设计强度之前，扭转刚度相比建造成型后较低，这使得混凝土桥面板在施工期间对侧向失稳更加敏感，因此，有必要对组合梁桥的施工过程中的力学性能以及施工影响因素等方面开展深入研究[4-7]。

该文以某匝道桥为依托，选取单跨简支梁，以有限元软件abaqus构建了三类不同的有限元模型，对影响施工过程组合箱梁弯扭稳定性的混凝土浇筑顺序、波形顶板对钢箱的约束作用、波形顶板的厚度、不同初始缺陷等因素进行了屈曲敏感性研究。通过计入初始缺陷对不同构造参数的梁桥屈曲全过程进行跟踪分析，总结了不同构造参数的梁桥屈曲极限承载力的变化趋势和屈曲后行为的变化规律。

1 工程背景

选取京德高速某匝道桥为分析对象，该桥为简支梁桥，箱梁长57 m，宽3.9 m，高2.0 m，断面尺寸见图 1。该桥下部由一个钢箱制成，钢箱上安装波形板顶板，作为现浇混凝土浇筑的模板，顶板上现浇混凝土车道，波形板同时起到提高施工期间箱梁的整体稳定性的作用。钢箱采用Q345D型钢材;波形板分别采用0.774 mm、0.86 mm和0.946 mm三种厚度，波宽×波长×波高尺寸为0.95 m×3.4 m×0.045 m或0.95 m×2.8 m×0.045 m，钢箱内设间距5 m的横隔板。对该简支梁桥进行了动力特性试验，得到其一阶弯曲自振频率，试验结果主要用于验证建模方法的正确性。

2 弯曲竖向振动方程的建立

该研究是关于施工期间桥梁荷载响应的计算。在桥面板混凝土硬化过程中，存在侧向失稳的风险，因此在施工期间稳定性分析至关重要。计算采用考虑初始缺陷的二阶微分方程。假设缺陷以初始扭转φ0（x）和水平初始倾角v0（x）存在，并假定初始扭转呈正弦曲线，最大值约为0.3%。1°初始倾角也假设为正弦，最大振幅为30 mm。桥梁的响应由以下微分方程控制：

（1）

（2）

式中：Kw为扇形惯性矩（m6），GKv表示扭转刚度（Nm2），KwC表示瓦格纳系数（Nm2）。

3 有限元建模

3.1 有限元计算模型

采用ABAQUS建模，钢箱梁材料采用Q345D，应力-应变曲线用双折线模型模拟。为了更好地模拟钢材的局部屈曲现象，钢板采用壳体单元S4R，全局网格尺寸为0.24 m。在结构化网格划分时，根據估算的结构应力梯度，对相应区域进行网格加密或稀疏。桥梁两端的支座约束为：桥梁一端的支座约束所有平移自由度，而另一端的支座仅约束轴向和横向。

3.2 施工过程模拟

钢箱混凝土组合梁桥的整体刚度主要由钢箱桥、波形钢顶板、混凝土桥面板贡献，在施工过程中钢箱梁的受力及钢箱梁的扭转翘曲约束随施工进程而改变，结构的整体刚度随施工进度而变化。为保证桥梁施工安全，须对施工顺序、施工过程荷载变化进行合理的施工模拟分析。

考虑荷载包括，模板、施工荷载、自重、风荷载和浇筑混凝土荷载。在浇筑过程中，活荷载为风荷载和桥面混凝土板浇筑混凝土荷载。

构建三类模型进行分析，用于研究影响结构刚度及弯扭稳定性的影响因素：仅由钢箱梁组成的MD1;由钢箱梁MD1及通过可靠连接方式与MD1翼缘顶板连接的波形板组成的模型MD2;除桥台处，在钢箱梁MD1顶部通过可靠连接设置波形顶板，提供部分封闭的横截面MD3。有限元模拟的施工过程主要包括以下步骤：

（1）施加结构重力。荷载1，5 kN/m2的压力荷载在顶面，代表结构模板。

（2）施加风荷载等。荷载2，1.5 kN/m2的压力荷载，横向作用于结构上，代表风荷载;荷载3，45 kN/m2的附加压力荷载，在顶部的中心部分，表示浇筑混凝土的平面;荷载4，分级施加浇筑混凝土设计荷载，每级加载为混凝土桥面板自重设计荷载Pu的10%，每级分5个分步。

为模拟真实的加载情况及保证有限元计算能够快速收敛，加载方式采用分步加载，并对三个模型分别加载分析。

4 结果分析

4.1 后屈曲分析

后屈曲分析旨在分析同影响因素下桥梁的响应，包括应力和变形。首先使用Lanczos特征值求解器进行线性特征值预测，在跨中每个翼缘顶板顶面施加三个集中力，以产生扰动，得到（恒荷载+活荷载）作用下组合梁的1阶屈曲模态，用以模拟分析对象中的初始几何缺陷，初始几何缺陷系数分别采用0、0.01、0.05、0.1、0.2，并引入了三种局部屈曲模式，比例因子均为0.001。

MD1旨在证明开口截面箱梁横向扭转稳定性的灵敏度。线性特征值预测的一阶整体屈曲模态见图2。

4.2 影响钢桥扭转稳定性的主要因素

通过上述三类模型的有限元分析，进而研究桥面混凝土浇筑顺序、波形钢顶板厚度，分析在铺设和未铺设波形钢顶板的两种情况下对结构弯扭稳定性的影响。

4.2.1 波形钢顶板铺设的影响

图3反映了桥面板混凝土不同浇筑完成比例的荷载作用下，0.1Pu到1.0Pu不同荷载层级作用下翼缘板的挠度随跨度分布曲线。

翼缘板1与翼缘板2的节点竖向位移量之间存在明显差异，而它们的横向位移几乎相同。这是由于绕纵轴扭转，使得翼缘板1降低到翼缘板2的1/3。

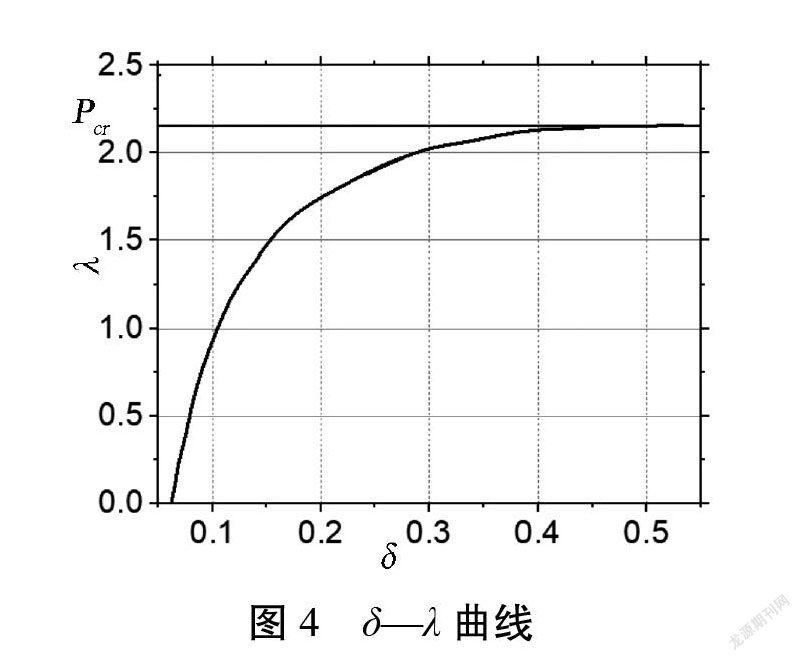
在恒+活工况下，采用结构的一阶屈曲模态作为初始缺陷分布模态，初始几何缺陷系数为0.01，对结构进行荷载-位移全过程屈曲分析，得到图4，其中，x轴表示沿路径翼缘板1的最大横向位移，而y轴为浇筑混凝土的荷载比例系数。结构的屈曲系数，可达2.16，Pcr为屈曲临界荷载。

并根据标准（一阶）Southwell plot分析方法[8-10]求得弹性屈曲临界荷载，具体做法是y轴为，x轴为δ，P为分级施加的荷载。根据这些分布点拟合曲线，曲线斜率为θ，屈曲系数λcr=1/θ，针对MD1所绘的Southwell plot曲线具体见图5。

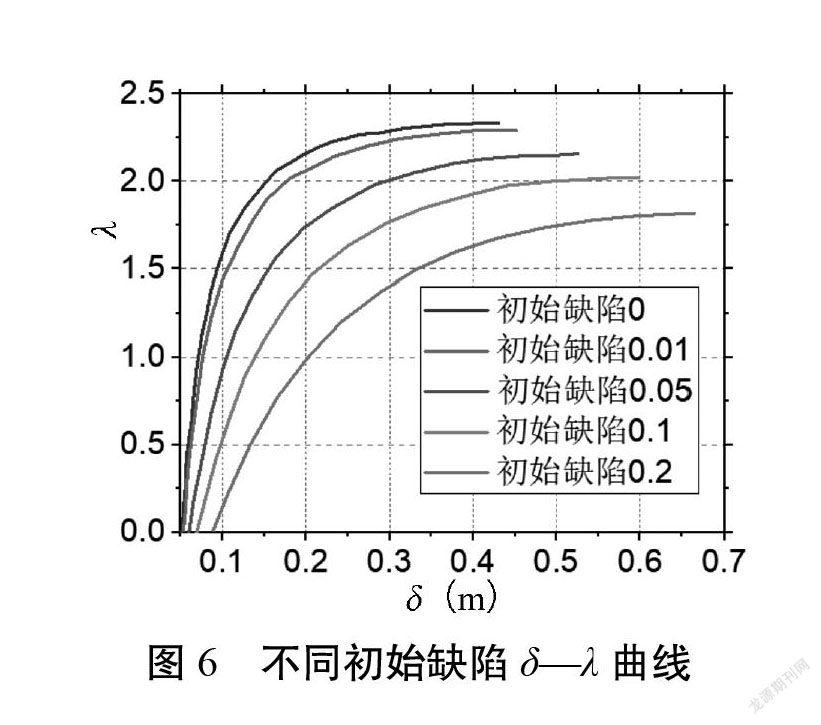
针对MD1绘制了不同初始缺陷的曲线，见图6，并给出了不同初始缺陷下Southwell plot曲线，见图7，可得不同初始缺陷条件0、0.01、0.05、0.1、0.2对应的屈曲系数分别为2.446、2.427、2.314、2.153、1.988。

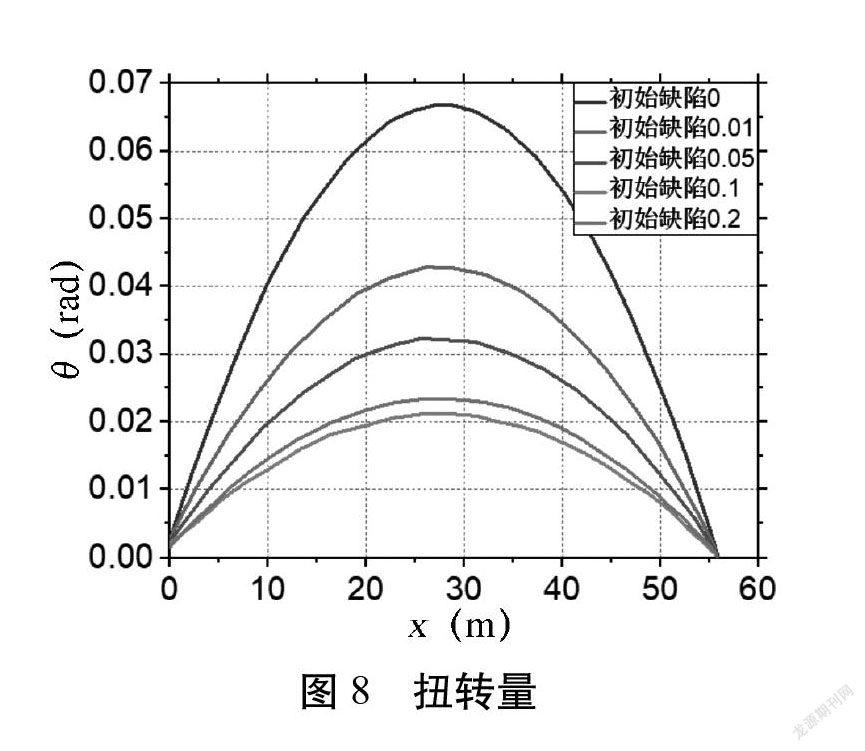
不同初始缺陷条件下，桥梁沿长轴向扭转近似为二次曲线，见图8。初始缺陷的增加也会产生相对较大的结构扭转。

分析表明，随着初始缺陷的增加，结构扭转和横向位移相对较大，而极限荷载相应降低。

图9显示了MD2的竖向位移云图。

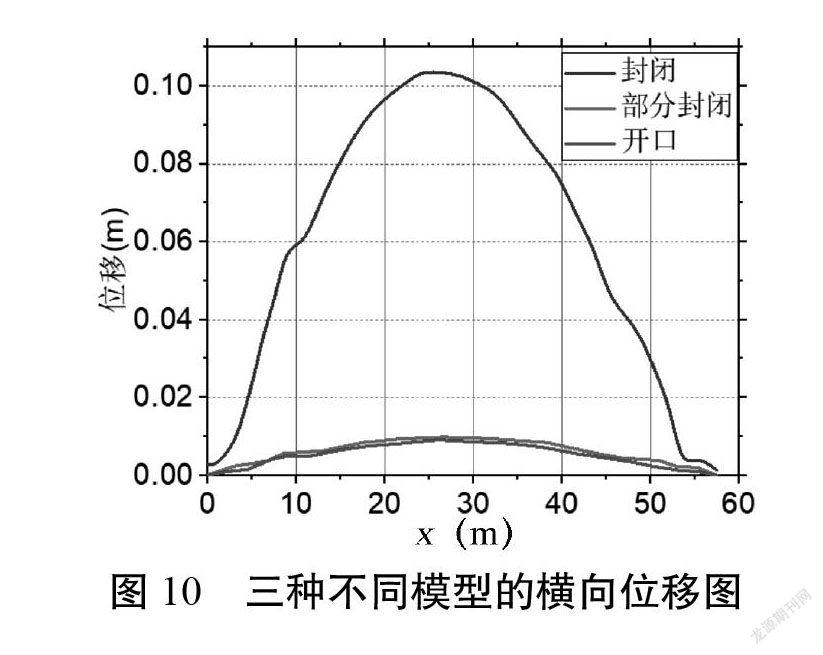
图10显示了MD1～3这三种不同模型翼缘板1沿跨径的横向位移，初始缺陷为0.05。对以上三种不同模型之间的位移和扭转进行比较表明，MD2、MD3的位移和扭转仅为MD1的10%，MD1的最大侧向位移为0.109 m，MD2的最大侧向位移为0.017 7 m，MD3的最大侧向位移为0.018 1 m。

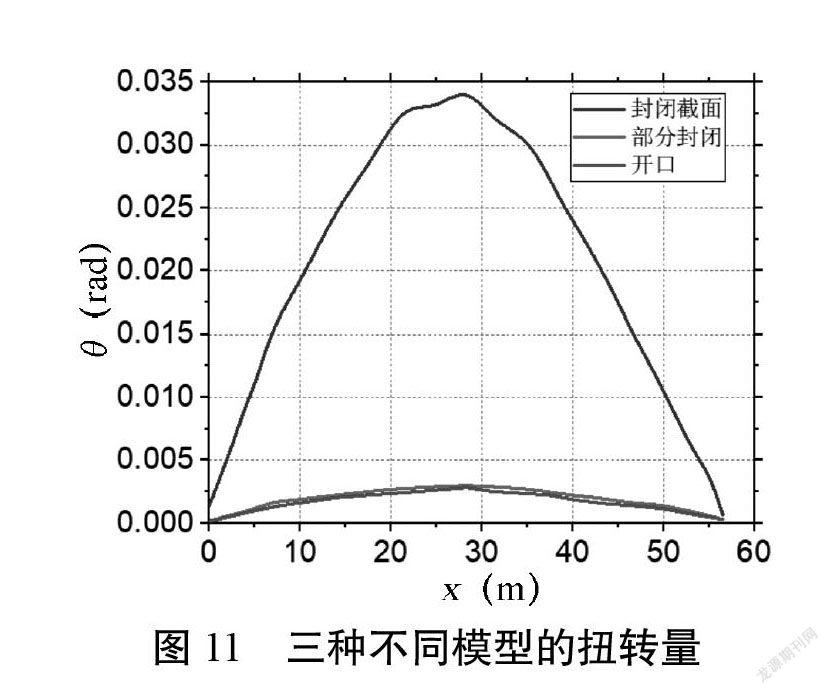
图11显示了三种模型的扭转量。MD1的扭转量大约是MD2、MD3扭转量的10倍。施工期间，桥梁的主要问题不是应力，而是扭转和侧移量。

4.2.2 波形顶板厚度的影响

在相同边界条件和相同荷载作用下，针对MD2，以相同波纹型号但波形顶板厚度变化作为影响因素，进行了屈曲特征值分析，结果表明：在经济厚度范围内，随着波形顶板厚度的增加，抗屈曲性能提高。计入结构尺寸初始缺陷的影响进行非线性分析，结果表明：将初始缺陷从0.01增加到0.05可使横向位移增加36%。进一步从0.05增加到0.1，侧向位移增加24%，从0.1增加到0.2，最终侧向位移增加52%。结果表明：初始缺陷的增加会显著增加侧向位移。

4.2.3 桥面板混凝土浇筑顺序的影响

为分析顺序施工引起的分层加载的影响，桥面板混凝土浇筑顺序分为两种方案，方案1：先从桥梁中心浇筑，逐步向两侧桥台展开;方案2：改变浇筑程序，从桥梁端部浇筑开始。通过计算分析，方案2可增加结构施工期间的扭转翘曲约束，提高结构弯扭稳定性。

5 结论

（1）当使用波形顶板创建闭合横截面时，与开口的横截面相比，扭转和横向位移显著减少。

（2）为增加结构的可靠性冗余度，在波形板整体失稳情况下，要保证开口横截面的箱梁应能够持续工作。

（3）初始缺陷的大小对桥梁性能有很大影响。初始缺陷的增加会导致较大的扭转、横向位移，及极限荷载的降低。如果扭转变大，未凝固的混凝土将向桥梁一侧移动，作为偏心荷载，进一步扭转增大。

参考文献

[1]朱劲松.钢箱-混凝土组合梁桥竖向温度梯度分析[J].公路工程，2021（7）： 76-82.

[2]樊健生， 聂建国， 吴道闻 . 钢 - 混凝土组合梁弹性屈曲的力学性能 [J]. 清华大学学报， 2004（6）： 786-788.

[3]白玲. 超静定组合结构桥梁受力特性的3D-FEM模拟分析[D]. 北京：铁道科学研究院， 2003.

[4]王景全， 吕志涛， 刘钊. 部分剪力连接钢-混凝土组合梁变形计算的组合系数法[J]. 东南大学学报， 2005（Z1）： 5-10.

[5]陈斌. 钢与混凝土组合梁受力性能分析[D]. 长沙：湖南大学， 2008.

[6]邵长宇. 大跨度钢-混凝土连续组合箱梁桥关键技术研究[D]. 上海：同济大学， 2006.

[7]刘佳. 大跨度钢-混凝土连续组合梁桥施工过程有限元分析[D]. 武汉：华中科技大学， 2012.

[8]Karnik Aggarwal，Sa m Wu， John Papangelis. Finite ele ment analysis of local shear buckling in corrugated web bea ms[J]. Engineering Structures， 2018（162）： 37-50.

[9]Wu Cheng-Song， Hassanein M.F.， Deng Hao， et al. Shear buckling response of S690 steel plate girders with corrugated webs[J]. Thin-Walled Structures， 2020， 157.

[10]袁建紅， 朱锡， 张振华. 水下爆炸载荷作用下环肋加筋圆柱壳结构的弹塑性动力屈曲[J]. 爆炸与冲击， 2012

（6）： 585-591.