基于多/单比特切换机制的LDPC码两级WBF算法

周 华，张 锐，葛旗伟，史传胜

(南京信息工程大学 电子与信息工程学院，南京 210044)

0 引 言

低密度奇偶校验(Low Density Parity Check, LDPC)码[1]是一种逼近香农极限的好码，其译码算法可分为硬判决译码和软判决译码算法。软判决译码算法通过校验节点和变量节点之间的软信息传递更新，常用算法有置信传播(Belief Propagation, BP)算法[2]、最小和算法[3]和基于上述算法提出的一些改进算法[4-5]；硬判决译码算法每次迭代时翻转不满足校验方程个数最多的比特，主要代表算法为比特翻转(Bit-Flipping, BF)算法[1]。由于硬判决译码算法并没有对可靠度软信息进行考量，故其具有复杂度低和运算量小等特点，但译码性能不如软判决译码算法。为了改善BF算法的译码性能，在此基础上提出了加权比特翻转(Weighted Bit Flipping,WBF)译码算法[6],该算法首次将可靠度软信息引入到BF算法中;文献[7-10]对WBF译码算法翻转函数和权重计算进行改进，取得了一定的译码性能提升;文献[11]提出的基于幅度和的WBF(Sum of the Magnitude based WBF,SMWBF)译码算法提出了一种新的权重计算来衡量比特的可靠性;文献[12]在SMWBF译码算法基础上提出了基于变量节点更新的SMWBF(Variable Node Updating based SMWBF,VSMWBF)译码算法，使性能获得了进一步的提升。

但以上算法在每次迭代中只能翻转一个比特且VSMWBF译码算法由于比特幅值发生变化，需要重新计算权重，使得译码时间较长，迭代收敛速度较慢。为了提高算法的译码速度，本文在SMWBF和VSMWBF译码算法基础上提出了一种具有全新跳转条件的多/单BF切换机制的两级译码算法。仿真表明，与单独采用SMWBF或VSMWBF译码算法相比，本文所提算法在提升译码性能和降低平均迭代次数方面都取得了一定成效。

1 基于LDPC码的BF译码算法

1.1 基本定义

用(N,K)(dv,dc)表示有固定行重dc、列重dv和码率为R=K/N的规则二进制LDPC码，其中，N为码长，K为信息位，其对应的奇偶校验矩阵记为H=[hmn]，H为M行N列矩阵。用集合N(m)={n∶hmn=1}表示H第m行中所有“1”的位置，即与校验节点m相连的变量节点集合；用集合M(n)={m∶hmn=1}表示H第n列中所有“1”的位置，即与变量节点n相连的校验节点集合。设发送码字c={c1,c2,…,cn}经过二进制相移键控(Binary Phase Shift Keying, BPSK)调制后得到双极性码字序列{2c1-1,2c2-1,…,2cn-1},通过加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道得到接收码字y={y1,y2,…,yn} ，其中yi=(2ci-1)+vi，vi为均值为0、功率谱密度为N0/2 (即方差σ2=N0/2)的高斯白噪声。根据硬判决规则得到二进制码字序z={z1,z2,…,zn},其中：

接收序列的伴随式为s=[s1,s2,…,sn]=zHT，译码算法成功的标志为伴随式为全零矩阵。定义接收序列中各码元信道观测值的初始化对数似然比Li为

式中：P()为概率函数；Eb/N0为信息位信噪比(Signal Noise Ratio ,SNR)。由上式可知，比特i可靠度软信息的|Li|与其幅值(信道观测值)|yi|成正比例关系，因此下述几种改进的WBF译码算法均用幅值|yi|代替|Li|作为可靠度软信息。

1.2 SMWBF译码算法

修正加权比特翻转(Modified WBF, MWBF)[7]和改进的修正加权比特翻转 (Improved Modified WBF, IMWBF)[8]译码算法在计算权重时认为，参与某个校验方程的所有变量节点中具有最小幅值的节点对此校验方程的影响最大，而SMWBF译码算法[11]则认为参与每一个校验方程的所有变量节点的幅值大小均会对结果造成不同程度的影响。其在计算比特n的权重时，将除了自身外其他变量节点幅值的和作为权重，故SMWBF译码算法的权重计算公式为

(3)

SMWBF算法对应的翻转函数为

式中，α为权重因子，用来修正变量节点对判决带来的过度影响。

SMWBF算法步骤详述如下：

步骤1 初始化：设置初始迭代次数k=1,并设定上限kmax，zk和sk为第k次迭代译码的输出序列及其伴随式。

步骤2 通过式(3)计算权重ωmn。

步骤3 计算伴随式：

若sk为全零矩阵或达到预设的最大迭代次数，则跳至步骤7；反之，进行步骤4。

步骤4 由式(4)计算各个变量节点的翻转函数。

步骤5 翻转最大En值所对应的比特：

步骤6k=k+1,转至步骤3。

步骤7 输出zk，译码结束。

1.3 VSMWBF译码算法

由于SMWBF等WBF译码算法在一次迭代过程中，变量节点自身的可靠度信息并未更新，通过考虑软判决译码算法的变量节点和校验节点软信息交替更新的思想，VSMWBF[12]译码算法对SMWBF译码算法步骤5和6进行修正，即在每次迭代过程中，人为扩大被翻转变量节点的幅值，并在下一次迭代中重新计算权重，以此来体现这种可靠度的增加，在每次迭代后变量节点和校验节点都实现更新。从而使翻转函数En的计算更加精确，故译码性能取得进一步改善。将SMWBF译码算法的步骤5和6做如下调整，即可得到VSMWBF算法的译码步骤。

步骤5 翻转最大En值所对应的比特，同时将其幅值扩大β倍。

步骤6k=k+1，算法转至步骤2。

2 本文算法描述

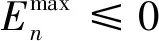
图1 多/单BF切换机制

2.1 第一级译码器

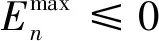
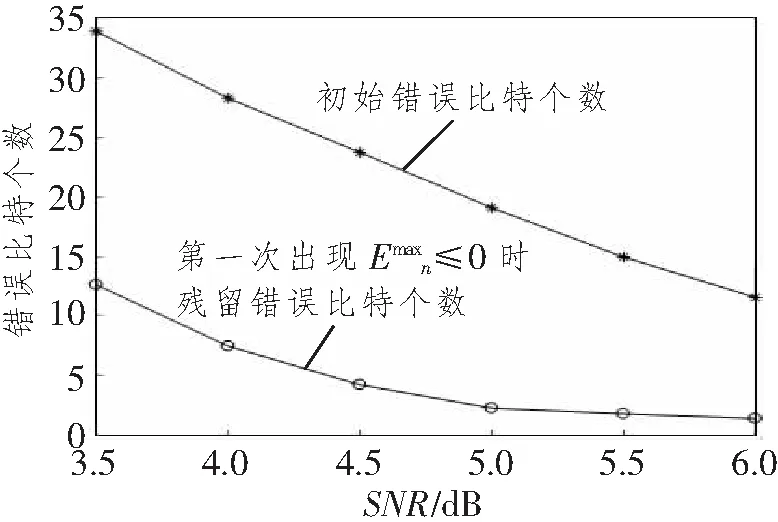
图2 第一次出现时的残留错误比特

如图3所示，若对残留错误比特依旧进行多BF译码会导致译码性能不佳，而使用单BF译码来接替译码任务，相较于此时停止译码，性能会得到进一步提升，故本文提出了多BF向单BF切换的两级WBF译码机制。

图3 出现之后进行不同的译码选择对译码性能的影响

第一级多BF译码器对SMWBF译码算法步骤5调整如下：

2.2 第二级译码器

表1所示为第一级译码器陷入循环的概率表，由表可知，若第k次与第k+1次译码时所翻转的比特位一致，则在后续迭代中，此变量节点将被无限循环翻转。为避免这种情况，本文在第一级译码器中引入了循环检测装置，当检测到连续两次迭代的翻转比特位置相同时，跳到第二级译码器中，从而避免了无限循环，而VSMWBF译码算法在每次迭代后都会更新变量节点的幅值，故该算法不会出现无限循环翻转现象，从而消除了整个译码器的无限循环翻转。由此，本文算法选择VSMWBF译码算法作为第二级单BF译码器的译码算法。

表1 第一级译码器陷入循环的概率

2.3 本文算法步骤及流程图

综上，如图4所示，本文算法步骤如下：

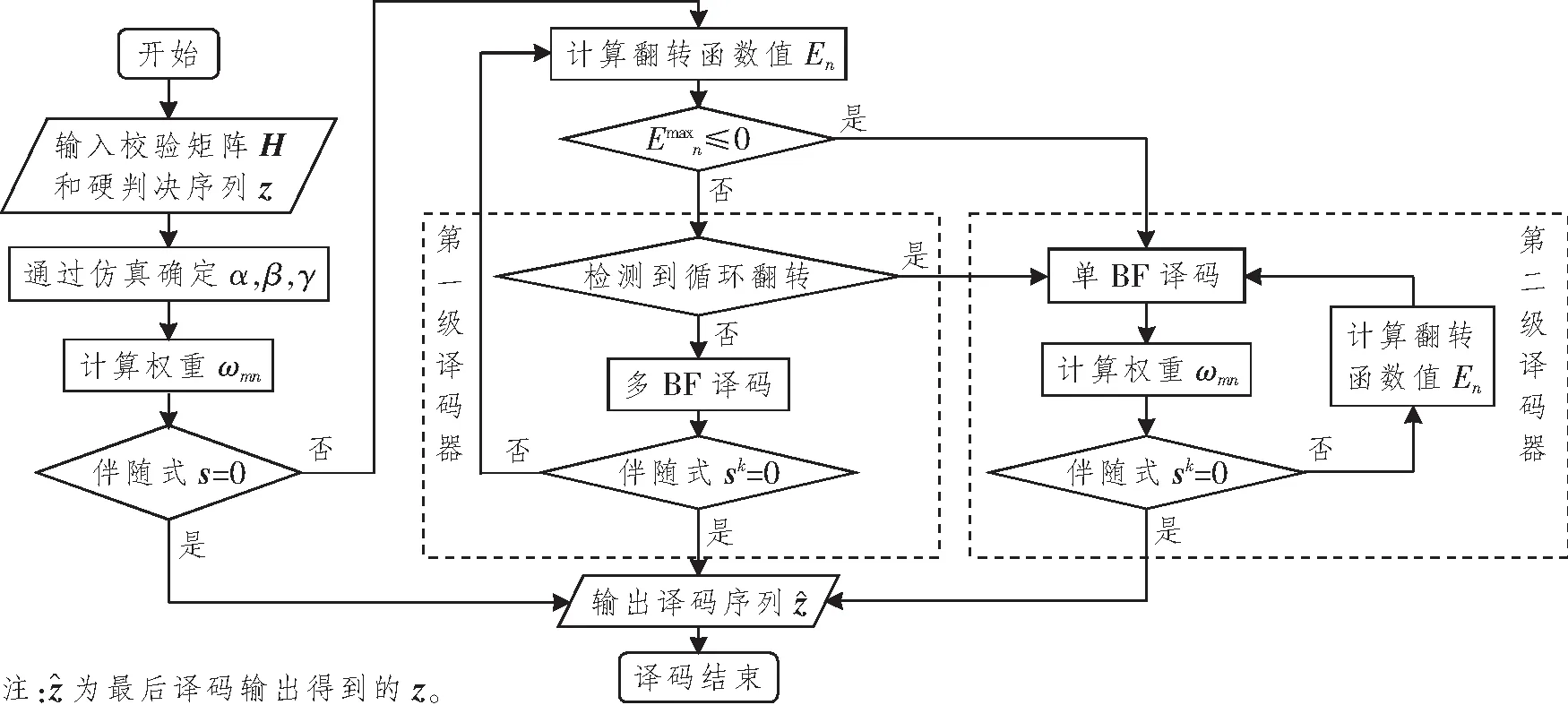
图4 算法流程

步骤1 初始化：设置初始迭代次数k=1,并设定上限kmax，通过仿真确定参数α、β和γ。

步骤2 通过式(3)计算权重ωmn。

步骤3 计算伴随式：

若sk为全零向量，或达到预设的最大迭代次数，则进行步骤8；反之，进行步骤4。

步骤4 由式(4)计算各个变量节点的翻转函数En。

步骤6 启动第一级译码器对zk进行译码，同时记录第k次翻转位置，并与第k-1次翻转位置进行比较，若翻转位置完全相同，取消翻转并跳至步骤7；否则k=k+1，返回步骤3。

步骤7 启动第二级译码器对zk进行译码，并更新伴随式sk，若sk为全零矩阵或达到预设的最大迭代次数，则进行步骤8；否则k=k+1，重复步骤7。

步骤8 译码结束，输出zk。

3 仿真分析

本文仿真采用码率为1/2、列重为4和行重为8的(504，252)Gallager-LDPC规则码(码1)以及码率为1/2、列重为3的(1008，504)P渐进边增长(Progressive-edge-growth，PEG)-LDPC码(码2)。由于本文算法涉及3个不同的参数即加权因子α、扩大倍数β和阈值参数γ，故启动译码器前先通过仿真找出最佳的参数值。

3.1 阈值参数γ的选取

加权因子α为第一级和第二级译码器翻转函数的一部分，扩大倍数β为第二级译码器中可靠度的增加幅度，其取值会对翻转函数En和幅值|yn|造成影响，而阈值参数γ的取值只会影响翻转比特的个数，对En和|yn|并无影响，因此α和β的取值并不会影响γ，γ独立于α和β，故在对γ进行仿真时，固定α和β的取值。图5所示为码1和码2在γ取不同值时对译码性能的影响，最大迭代次数分别为50和100。

图5 γ取值对译码性能的影响

在译码性能方面，如图5所示，γ取值越小，译码性能越差。造成此现象的原因是，若γ取值太小，则会导致每次迭代中翻转过多的比特，使翻转正确比特的概率增大，从而影响译码性能；若γ取值过大，则每次迭代翻转的比特数较少，不能有效降低迭代的收敛速度。本文选取γ=0.8为码1的最优阈值参数，γ=0.7为码2的最优阈值参数。

3.2 加权因子α和扩大倍数β的选取

文献[8]和[12]指出，不同SNR的最优α和β可通过仿真找到，但为了便于分析，本文借鉴文献[12]中对α和β联合仿真的方法，选择一个不变的α和β。由上节可知，阈值参数γ独立于α和β，在分别对码1和码2做在不同SNR下α和β对译码性能影响的联合仿真时，固定γ，联合仿真图如图6所示。

图6 α和β的取值对译码性能的影响

由图可知，码1的α和β选为11和0.7时性能较好，码2的α和β选为11和0.4时性能较好。

3.3 译码性能分析

图7(a)为码1在最大迭代次数为50次时各WBF译码算法下的译码性能比较，两种码字的参数分别设定为3.1和3.2节仿真得到的对应参数值，由图可知，本文算法相较于VSMWBF译码算法有进一步提升，在误比特率为10-4处能获得约0.2 dB的增益；而在最大迭代为25次时，如图8(a)所示，在误比特率为10-4处相较于VSMWBF译码算法能获得约1 dB增益,在SNR=5 dB时，误比特率由10-3数量级提高到10-4，由此可知，在降低最大迭代次数时，改进算法译码性能相较于其他算法受影响较小，优势更为显著。通过观察图7(b)和图8(b)，码2可获得类似结论。

图7 译码性能比较

图8 降低最大迭代次数时的译码性能比较

3.4 译码平均迭代次数与译码时间分析

如图9(a)所示，本文算法在平均迭代次数上相较于其他WBF译码算法有明显改善，码1在SNR=4.5 dB时，IMWBF-2SBF[14]、VSMWBF和SMWBF译码算法均需要平均迭代25次以上才可完成译码，本文算法平均需迭代约13次即可完成译码，降低比例约50%。通过观察图9(b)，码2可获得类似改进。

图9 平均迭代次数比较

表2所示为SMWBF、VSMWBF和本文算法在SNR=4.5、5.0和5.5 dB时平均迭代次数对比情况。表3所示为3种算法在Matlab仿真平台分别在SNR=4.5、5.0和5.5 dB时模拟对20万个码字完成译码所需时间对比情况。码1的参数分别设定为3.1和3.2节仿真得到的对应参数值，实验所用计算机的配置为内存16 GB，CPU为Intel Core i7-10875H 2.30 GHz的台式计算机。

如表2所示，本文所提算法相较于SMWBF译码算法，平均迭代次数在3种SNR情况下分别降低至48.7%、43.7%和43.4%，大幅降低了迭代收敛速度。如表3所示,相比于VSMWBF译码算法，译码所需时间降低至28.2%、24.2%和26.1%，显著缩短了算法的译码时间。

表2 码1在不同SNR下各WBF译码算法的平均迭代次数

表3 码1在不同SNR下各WBF算法对20万随机码字完成译码所需时间

4 结束语

本文通过发现多BF译码出现最大翻转函数值小于零时，采用单BF接替译码会提升译码性能，提出了一种全新的多/单比特切换条件将一种提前终止的判决门限多BF机制和单BF译码串联，形成了一种多/单比特切换的两级译码机制。该机制融合了多BF译码收敛速度快和单BF译码算法低误比特率的两个优点。仿真表明，该方法在加快译码时间和收敛速度的同时，译码性能较SMWBF和VSMWBF等译码算法有所提升，并在最大迭代次数设定较小时优势更为显著。

为了消除整个译码器的循环翻转现象，本文算法选择了VSMWBF译码算法作为第二级译码器，代价是增加了额外的参数扩大倍数β，因此在译码开始时需对3个参数进行仿真选取，增加了额外的工作量。在以后的研究中，是否有更简捷的方式来确定参数或者基于本文提出的机制可以选择其他优秀的单比特译码算法作为第二级译码器，需要继续加以探究。