大规模MIMO系统混合线性迭代信号检测算法

张晓华，彭 小 ，黄 龙

(重庆市信息通信咨询设计院有限公司，重庆 400041)

0 引 言

大规模多输入多输出(Multiple-Input Multiple-Output, MIMO)系统[1-4]中，传统线性检测算法迫零 (Zero-Forcing,ZF)与最小均方差 (Minimum Mean Square Error, MMSE)算法[5-7]的复杂度主要来源于大矩阵反演运算，计算复杂度为O(K3)。为降低高维矩阵求逆复杂度，国内外学者相继提出了多种基于MMSE检测方案的低复杂度改进算法，主要有级数展开类近似法[8-9]、迭代类近似求解法[10]和基于矩阵梯度搜索近似求解法[11]等。级数展开类近似法主要是利用Neumann级数展开法来近似获得MMSE检测器加权矩阵的逆矩阵，但是当展开阶数i增大时(i>2)，其计算复杂度将超过MMSE加权矩阵求逆的计算复杂度，所以只有i≤2时，Neumann级数近似算法才能把计算复杂度从O(K3)降到O(K2)；迭代类近似求解法则通过求解线性方程来估计用户发送矢量代替MMSE检测器加权矩阵的求逆过程[12]，部分学者提出了多种近似算法，如理查德森(RIchardson, RI)迭代法、高斯(Gauss-Seidel, GS)迭代法、雅克比(Jacobi, JC)迭代以及连续超松弛(Successive Over-Relaxation, SOR)迭代法，虽然这些迭代算法可以将计算复杂度降低一个数量级，但在收敛性方面不是太理想。

本文提出了一种混合线性迭代(Mixed Linear Iteration，MLI)信号检测算法，首先构造MMSE检测器加权矩阵的分裂矩阵形式，再把展开阶数为2(i=2)的加权矩阵逆矩阵的Neumann级数展开式转换为迭代矢量初始值代入迭代方程，从而进一步加快算法的收敛速率，以较少的迭代次数逼近MMSE算法的性能曲线。

1 系统模型

假设在大规模MIMO系统的上行链路中，基站(Base Station, BS)配置的天线数为M，同时与N个单天线用户进行数据的传输，且N>M，并假设信号通过瑞利衰落信道传输。实际中的大规模MIMO通信系统较为复杂，为了便于分析理解，本文只对相对简单的MIMO系统模型进行分析，令xc=[x1,x2,…,xM]T∈CM×1为所有用户同时发送的M×1维信号矢量，Hc∈CN×M为瑞利衰落大规模MIMO信道矩阵，则接收信号模型可表示为

式中：yc=[y1,y2,…,yN]T∈CN×1为接收到的N×1维信号矢量；nc=[n1,n2,…,nN]T∈CN×1为N×1维加性高斯白噪声。为降低复数运算的复杂性，将式(1)转化为实数形式为

式中，y∈R2N×1，x∈R2M×1，n∈R2N×1及H∈R2N×2M，R为不同维度的矩阵，则式(2)可表示为

式中：R(·)为实部；J(·)为虚部。

2 Neumann级数展开

大规模MIMO信号检测算法性能较好的一般计算复杂度都较高，为找到两者间的折中算法，Wu等人[9]提出利用一系列矩阵乘法之和来近似矩阵求逆结果的Neumann级数展开法来近似获得MMSE加权矩阵H的求逆结果，当存在可逆矩阵X近似W且满足：

式中，I为单位矩阵，那么W的逆矩阵可以根据Neumann级数展开为

式中，矩阵W可分解为D和E，即W=D+E，E为W的空心矩阵，D为W的严格对角矩阵。当N≫K时，由于MIMO系统信道硬化的特性，加权矩阵W具有严格对角占优特性，可认为W≈D。将式(6)中的W和X分别用D+E和D代替可得：

式(7)的收敛条件为

若只展开W-1矩阵Neumann级数的前i项，则式(7)可转换为

分析可知，采用Neumann级数展开的方法，当取i<2时，可通过较低的计算复杂度来近似表示W-1；当i=2时，可以计算复杂度为O(K2)来近似W-1，可较好地降低W矩阵求逆过程的计算复杂度；但当i>2时，其计算复杂度将达到甚至超过O(K3)。

3 基于Neumann级数展开和矩阵分块的线性迭代算法

3.1 MLI算法

本文提出的MLI算法首先采取对MMSE加权矩阵W进行分块预处理的方法，根据线性迭代算法的思想将式(4)转换成线性方程形式：

转换成线性方程的迭代解法形式并给出迭代收敛条件如下：

式中：ai,j为矩阵A第i行第j列的元素；Pi,j为矩阵P第i行第j列的元素。

分析可知，分裂矩阵P是由W矩阵对角上所有2×2子矩阵分块组成而其他位置为0的方式构造而成，这样将大大提高算法在硬件上的可实现性，具有很高的并行性，计算复杂度可降低为O(K2)。

综上所述，基于MLI算法的信号检测算法流程如下所示：

输入：信道衰落矩阵H，接收信号y；

初始化：

(1) 计算MMSE滤波矩阵W=G+∂2IM；

Neumann级数展开：

分块矩阵线性迭代：

(5) 根据式W=A=P+Q分解矩阵W；

(6) 根据式(15)构造分块矩阵P；

for (k=0;k≤N；k++)

end for

3.2 收敛性分析

线性迭代算法的收敛性与其迭代矩阵的特征值密切相关，用λn表示迭代矩阵-P-1Q的特征值，而其特征值对应的特征向量用ωT表示，则有：

将式(11)代入上式并作转换得：

令C=P-Q，由式(11)有：

结合式(19)，式(18)可表示为

由于A=G+∂2IM，G=HHH为格拉姆矩阵，对角元素为正；∂2=N0/Es为估计方差，其值大于或等于0，因此，矩阵A为正定矩阵。由正定矩阵的性质可知：

由于A是对角占优矩阵，矩阵C=P-Q继承了矩阵A的对角元素，因此，C具有矩阵的A特性，是正定对角占优矩阵。同理，C也满足：

综合式(20)、(21)和(22)得：

由式(23)可得：|λn|<1。所以迭代矩阵-P-1Q在迭代过程中是收敛的。

3.3 复杂度分析

对于BI算法的复杂度分析，首先将式(13)变形为

式中，矩阵P按照式(15)进行构造，由矩阵A对角上若干个2×2矩阵组成，每个2×2矩阵求逆的过程需要4次乘法和一次除法，则对于2M×2M的P矩阵需要4M次乘法和M次除法。Q是2M×2M矩阵，每行每列都有2M-2个非零元素，Xk为2M×1向量，依据矩阵与向量的乘法可以通过向量与向量乘法并行实现，可知QXk需要2M×(2M-2)次乘法；矩阵每行每列有两个非零元素，那么P-1每行每列也有两个非零元素，对于2M×2M的P-1与2M×1的向量b-QXk相乘则需要4M次乘法，采用i(i≥2)次迭代求解信号矢量需要4(i-1)M2+5M次乘法。

图1所示为MLI算法与MMSE检测算法、Neumann级数展开算法和GS算法复杂度之间的对比，图中i为不同算法迭代次数。结合Neumann级数展开与BI两部分的算法，MLI算法共需要(4i+8)M2+M次乘法，可见在任意迭代次数下，算法复杂度依然保持为O(K2)，相比较于MMSE检测算法，计算复杂度大大降低。

图1 算法复杂度对比

4 仿真结果分析

本节将以MMSE算法为比较基准，比较在不同天线规模和不同调制方式下，MLI算法的检测性能。

首先，假设信号在瑞利衰落信道下传输，采用正交幅度调制(Quadrature Amplitude Modulation,QAM)方法,将信号调制方式设置为64 QAM，天线的发射功率ES=1，下面将给出在天线规模为64×16的情况下，迭代初始值为零矢量的BI算法与迭代初始值为Neumann级数二阶展开值时BI算法的误码率(Bit Error Rate，BER)性能差异，仿真结果如图2所示。

由图2可知，当迭代次数i增加时，BI和MLI算法的检测性能都得到了不同程度的改善，但在相同的迭代次数下，MLI算法的检测性能有明显的优势。当迭代次数i=2且BER性能为10-2时，BI算法所需的信噪比(Signal-to-Noise Ratio，SNR)为14 dB，而MLI算法所需的SNR为12 dB，相比之下将获得近2 dB增益的性能提升；另外，把Neumann级数二阶展开式转换为BI算法的初始值后，由图可知，本文所提MLI算法曲线收敛更快，当i=4时，可近似MMSE最优检测算法的性能。

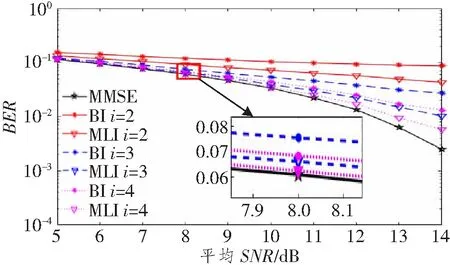
图2 BI与MLI算法在天线规模为64×16时的BER

图3(a)～(c)所示为在基带信号调制方式为64QAM的调制条件下，MMSE、Neumann级数展开、BI分块迭代以及MLI算法在天线规模N×K为64×16、128×16和256×16时的BER性能仿真结果。在相同的迭代次数下，MLI混合迭代算法的检测性能最好，且以较少的迭代次数超过了Neumann级数展开算法和BI算法较高展开阶数或迭代次数下的检测性能。

图3 64QAM调制下不同检测算法的BER性能对比

当BS侧的天线数量增加时，提供的分集增益增大，由图3(a)～(c)可知，不同算法的检测性能都随着BS天线数目与用户数比值的增加逐渐逼近MMSE检测算法性能，但在相同BER下，N×K为64×16时比为128×16时需要的SNR更高，而N×K为128×16时比为256×16时需要的SNR更高。所以当N/K的值增大时，相比于其他算法，本文所提MLI算法能以较少的迭代次数实现较优的检测性能。

5 结束语

基于Neumann级数展开和分块矩阵线性迭代算法，本文提出了将二阶Neumann级数展开转换为分块矩阵线性迭代算法初始值的MLI算法来近似处理复杂的MMSE检测算法矩阵求逆。本文详细证明了迭代矩阵的收敛性，且理论验证了该MLI算法的复杂度较低，能够在任意迭代次数下保持算法复杂度为O(K2)。Matlab仿真结果表明，MLI算法的检测性能要比Neumann级数展开法和零矢量BI算法更好，能够以较少的迭代次数逼近MMSE检测算法的性能曲线。通过对MLI算法进行计算复杂度分析和仿真分析可知，该算法有较低的计算复杂度和较快的收敛速度，能作为MIMO检测系统信号检测的有效方案之一。