基于MIMO电力线信道的定时同步算法

申 敏，毛文俊，袁一铭,李心安

(重庆邮电大学 a.通信与信息工程学院； b.新一代宽带移动通信重点实验室，重庆 400065)

0 引 言

电力线通信(Power Line Communication，PLC)受电力线网络本身以及接入负载的影响，具有多径衰落严重和噪声大等缺陷。正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术因其抗多径衰落能力强、频谱利用率高等优势，恰好能克服电力线本身的缺陷。利用保护地线(Protective Earth，PE)形成多输入多输出(Multiple-Input Multiple-Output，MIMO)的传输机制，可以提升电力线的通信速率[1]，在不需要增加额外带宽的情况下提升系统容量。

在MIMO PLC系统接收端需进行精准的定时同步，否则会产生严重的符号间干扰甚至载波间干扰。文献[2]提出了在两根发射天线发送同样的训练序列来实现MIMO系统同步；文献[3]为了提高MIMO-OFDM系统在平坦衰落信道和多径衰落信道下的同步性能，提出了一种将发射天线选择和接收端最大比合并(Maximum Ratio Combining，MRC)相结合的方案；文献[4]提出了一种利用差分相关的精同步方案，从而消除了粗同步阶段产生的“峰值平台”；文献[5]将延时相关函数与互相关函数合并实现了定时同步过程；文献[6]在接收端通过使用一组相关器提高了定时的正确率。上述算法不仅计算复杂度太高，且不适用于噪声环境复杂的PLC信道。

针对上述问题，本文提出了一种适用于MIMO PLC系统的定时同步算法，利用差分相关和MRC的联合算法来实现精准定时。仿真结果表明，与互相关算法相比，改进算法能够提高定时同步的正确率，且能有效降低计算复杂度。

1 MIMO PLC系统模型

1.1 信道模型

传统的PLC通过将单相线中的相线(Phase，P)和零线组合成一个发送端口和一个接收端口来完成通信的过程。MIMO PLC系统模型如图1所示，MIMO PLC系统利用额外的PE，通过P、中线(Neutral，N)和PE两两组合形成多个发送和接收端口。P-N、P-PE和N-PE可提供3组端口。根据基尔霍夫定律，3个输入信号的和必须为0，因此，只有其中的两个端口可以同时作为发送端口。在接收端，所有3个不同的接收端口都是可用的。另外，当数据网络传输信号不平衡时会产生共模(Common Mode，CM)接收端，构成第4个接收端。CM模式会造成很大的电磁辐射，因此本文中不考虑CM模式。

图1 MIMO PLC系统模型

MIMO PLC系统中，第i个发射端口的基带时域OFDM数据xi(n)由频域数据Xi(z)经过N点的快速傅里叶逆变换(Inverse Fast Fourier Transform，IFFT)得到：

式中：i为发射端口；z为频域数据；n为时域数据；j为虚数单位。

OFDM信号通过电力线传输，第y个接收端口的接收信号ry(n)可表示为

式中：Nt为发送端口的数量；hiy(n)为第i个发射端口与第y个接收端口的信道脉冲响应；wy(n)为第y个接收端口的噪声；*为卷积运算。由文献[7]可知，信号脉冲响应h(n)在频域上可表示为

式中：H(f)为h(n)的频域表示；f为频率；L为多路径传播数量；gi为第i条信道的增益；a0和a1为衰减参数；at为指数衰减因子；di为第i条信道的长度；Vp为信号的传输速度。

MIMO PLC信道模型采用文献[8]提出的2×2随机相位多径MIMO信道模型。首先利用文献[7]中的模型确定发射端口和接收端口均为P-N信道，然后基于P-N信道为其他信道添加衰减幅值Ai和随机相位φi。

1.2 噪声模型

本文中噪声模型选用Middleton Class A模型。Middleton Class A噪声模型是背景噪声和脉冲噪声的混合，由相互独立的高斯分量和脉冲分量叠加组成，因此该模型适用于电力线的噪声环境[1]，其概率密度p(x)函数为

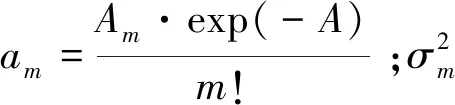
2 定时同步算法

2.1 MIMO PLC的帧结构

在MIMO PLC系统中，通过在各个端口发送不同的前导信号，在接收端利用前导信号的相关性和重复性进行同步信息的获取。每个发射端口的前导符号都由10.5个同步循环前缀(Synchronization Cyclic Prefix，SYNCP)和2.5个SYNCM(SYNCM 为SYNCP 取反后的符号)组成，SYNCM与SYNCP互为相反数。为了区分不同接收端口上的前导信号以及减少不同发射端口前导信号之间的干扰，在发送端通过相移器使不同发送端口上的前导信号SYNCP1和SYNCP2的相位相差π/2[9]。

2.2 现有定时同步算法

现有的定时同步算法大多利用训练符号的重复性和相关性来估计定时位置。

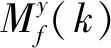
式中，s(m)为本地的训练序列。根据互相关函数的最大值位置可得到定时同步的位置。

2.3 改进的定时同步算法

本文提出的改进同步算法先用延时相关算法完成粗同步过程，再采用窗口求和来减小粗同步位置搜索范围，定时精同步采用差分相关及MRC的联合同步算法来实现精准定时。

(1) 定时粗同步

图2所示为MIMO PLC系统的定时粗同步算法框图。

图2 定时粗同步算法框图

利用前导信号的峰均比设定门限阈值，将大于门限阈值的样点进行限幅(clipping)非线性操作，滤除受脉冲噪声影响较大的信号幅值[10]。

对式(5)中的延时相关算法进行改进，从而降低计算复杂度：

通过式(8)可将N次乘法运算转化为两次乘法运算和两次加法运算，可有效降低算法的复杂度，便于硬件实现。

由于1帧中的前导信号是由多个SYNCP训练序列组成，为了更好地判断帧中前导信号的粗估计，设置N′=5×1 024为5个SYNCP的长度，替换式(8)中的常数N，以减小峰值平台。

图3 不加噪声时的延时相关曲线

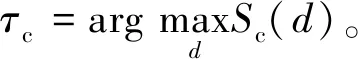
(2) 定时精同步

在第一阶段得到帧起始位置τc的基础上，可明确进行精同步接收数据的起始位置及范围并接收信号，将每个接收端口的信号与本地前导序列SYNCP1和SYNCP2分别进行差分相关，实现精准定时，处理过程如图4所示。

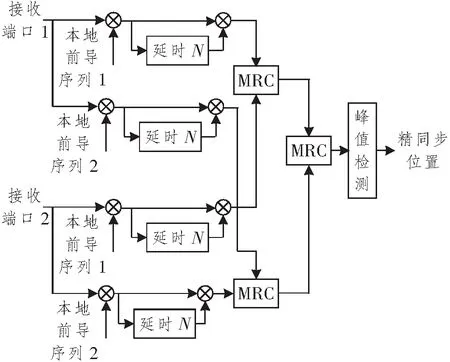
图4 定时精同步算法框图

将接收信号与已知前导进行共轭相乘，然后将得到的相关序列以间隔N计算差分相关:

式中，pi为本地的前导序列SYNCP1或SYNCP2。

有限范围内的差分相关如图5所示，由图可知，差分相关峰值远大于相邻相关值，且具有较好的抗噪声性能。

图5 信噪比(Signal-to-Noise Ratio，SNR)SNR=-5 dB时的差分相关示意图

3 仿真结果与分析

为了验证本文所提同步算法的性能，本节在MIMO PLC信道条件下进行1 000次蒙特卡洛仿真。仿真参数设置如表1所示。

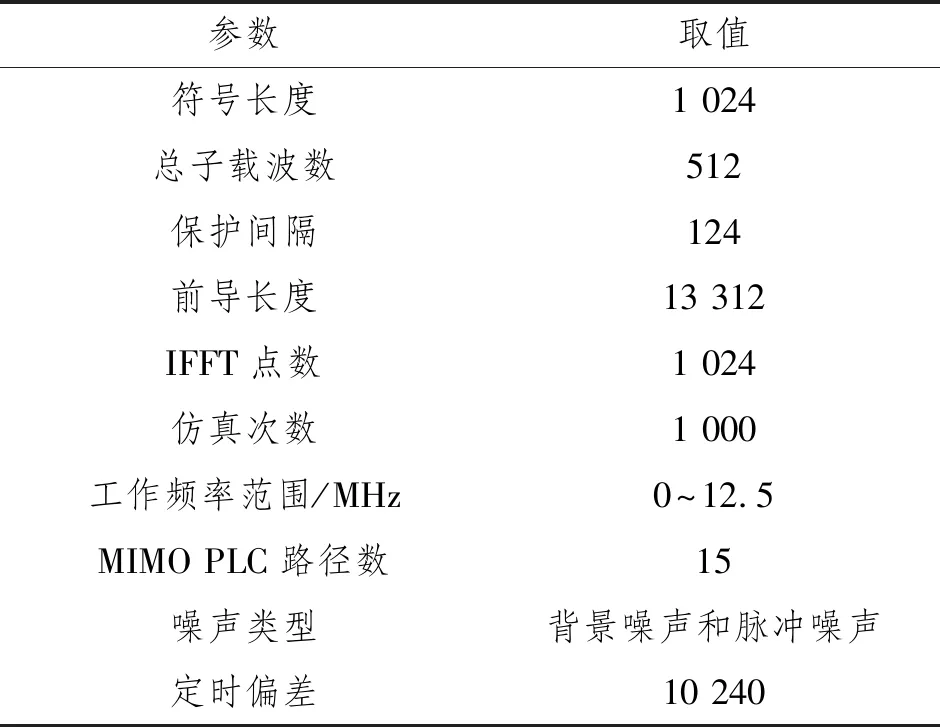
表1 仿真参数设置

图6所示为改进的定时粗同步算法的性能曲线，由于定时粗同步实现的是粗略估计，因此同步准确位置前后124采样点均假设为正确接收。由图6可知，本文所提改进延时自相关算法提高了定时粗同步的性能。

图6 粗同步的定时正确率对比

为了与现有算法进行同步性能比较，本文采用下面两种精同步算法：

算法1，文献[6]中的同步算法；

算法2，本文所提改进差分相关和MRC联合同步算法。

图7所示为上述两种算法的同步性能。由图可知，低SNR(SNR<0 dB)时，算法2的定时精度明显优于算法1，在定时同步正确率为90%时，算法2的SNR比算法1低2 dB。在SNR=4 dB时，本文所提算法的同步成功率达到100%。

图7 精同步的定时正确率

算法1与算法2的计算复杂度对比如表2所示。表中，L为接收数据的长度；N为前导序列的长度；N′为改进算法的滑动窗长；W为窗口求和的窗长；T为差分相关算法的滑动范围，T∈[τc-1 024,τc+1 024];L≫T,N。由于算法2只需在给定的小范围T内进行差分相关，相比算法1对长度为L的接收数据进行大范围的互相关操作，算法2计算量远低于算法1。

表2 计算复杂度对比

4 结束语

本文在PLC系统中存在随机脉冲噪声的恶劣环境下，提出了一种抵抗脉冲噪声干扰的MIMO PLC定时同步算法。在接收端先通过设置阈值过滤掉大部分脉冲噪声的干扰，并对传统的延时相关算法进行改进简化后续的计算过程；精同步通过差分相关和MRC来提高同步的精度。仿真表明，所提算法的同步性能有明显的提升，且复杂度有所降低。设置自适应门限提高第一主径判断的准确率，同时利用脉冲噪声在时域的稀疏性，应用压缩感知算法估计脉冲噪声的位置和强度将是未来的研究重点。