砂土中斜桩单桩水平承载与变形特性数值分析

赵爽，吴君涛，张日红，陈克伟，王奎华

(1.浙江大学滨海和城市岩土工程研究中心，浙江杭州，310058；2.浙江大学软弱土与环境土工教育部重点实验室，浙江杭州，310058；3.宁波中淳高科股份有限公司，浙江宁波，315000)

斜桩广泛应用于桥梁、海上风机、海洋平台等工程基础，用于抵抗风、浪等水平荷载。与竖直桩相比，斜桩由于能将部分水平荷载转换为轴向荷载，因而具有优良的水平承载性能[1]。由于桩身的倾斜布置，导致斜桩承载变形特性较竖直桩而言存在明显差异，因此有必要对斜桩的水平静力承载特性进行研究，以便更好地为实际工程服务。

斜桩的施工工艺相较竖直桩而言较为复杂，目前工程中使用的斜桩包括钻孔灌注桩和预制桩等。斜桩钻孔灌注桩施工主要通过在钻机底盘加焊钢板等调整钻机的斜率，进而进行斜向钻孔及桩身灌注[2]；而斜桩预制桩施工则主要采用吊桩将桩固定在预定斜率，之后通过调节打桩机导向架的斜率，使得桩锤、桩帽、桩身处于同一轴线，而后进行锤击沉桩[3]。目前，国内外学者针对斜桩的静力受荷特性展开了较多的研究。针对斜桩单桩的竖向静力承载特性，AL-NEAMI等[4]基于模型试验发现砂土中斜桩单桩的竖向承载力随倾斜角度呈抛物线变化，20°倾斜角度的斜桩单桩能提供最大的竖向承载力；SHARMA 等[5]通过模型试验发现在砂土地基中，当倾斜角度在30°范围以内时，斜桩单桩竖向承载力和竖直桩竖向承载力相当；曹卫平等[6-7]基于模型试验和数值模拟发现砂土中斜桩单桩的竖向承载力低于竖直桩竖向承载力，斜桩单桩的竖向承载力和倾斜角度呈负相关。

斜桩的设计初衷是在保证桩基竖向承载力的基础上，提升桩基的水平承载力，因此，斜桩的水平承载力更加受到学者的广泛关注。根据水平荷载方向与斜桩轴线的夹角，斜桩又经常被分为正斜桩和负斜桩[8]。吕凡任等[9-11]分别基于广义弹性理论法、Mindin 弹性解、变形楔模型进行了斜桩单桩水平极限承载力分析，研究结果表明，相较于竖直桩而言，负斜桩的水平承载力会有较大提升，而正斜桩的则显著降低；凌道盛等[12-13]分别基于桩侧被动区楔形体模型、模型试验构建了水平荷载作用下斜桩单桩水平极限承载力预测的修正p-y曲线法；ZHANG 等[14]采用离心模型试验探究不同密实度砂土地基中斜桩单桩的水平承载力，试验结果表明负斜桩的水平承载力比竖直桩的高，且桩周土越密实，该趋势越明显；RAJASHREE等[15-18]通过模型试验和数值模拟等手段，研究了不同倾斜角度、长径比的斜桩单桩在砂土地基中的水平受荷特性，结果表明负斜桩的水平承载力相较于竖直桩而言有较大的提升。但是，一方面，针对斜桩的研究普遍集中在承载力，而对斜桩相对于竖直桩的承载力改变机制、斜桩的荷载传递机理等缺乏相应的研究；另一方面，现有的斜桩水平承载力研究成果均集中在外力作用方向与桩身倾斜面处在同一个平面的情形，而对荷载与倾斜面呈一定角度斜交的情形研究较少。

综上所述，为了进一步探究斜桩的水平承载特性，本文基于数值模拟探究斜桩单桩基础在水平荷载作用下的桩身响应，研究不同倾斜角和加载角下斜桩单桩的水平受荷特性，提出水平荷载作用下斜桩单桩承载力的经验预测方法。

1 数值模型

1.1 数值模型的构建

本文中斜桩的定义如图1所示，当水平荷载方向与斜桩轴线夹角γ呈钝角时将其定义为负斜桩，γ为锐角时则为正斜桩。采用有限元软件ABAQUS对水平荷载下斜桩单桩的桩身响应及斜桩单桩承载力进行分析，选取摩尔-库仑模型模拟砂土性质的非线性。ABAQUS中根据桩-土表面定义接触属性以模拟桩-桩侧土之间的相互作用，本文中桩侧及桩底均采用主-从(master-slave)接触算法，选择刚度较大的桩面作为主控面，刚度较小的土体表面作为从属面，桩-土接触采用摩尔-库仑摩擦罚函数形式，界面摩擦因数选取u= tan(0.75φ)，其中，φ为桩周土的内摩擦角。采用六面体8节点线性缩减积分单元(C3D8R)构建有限元计算模型，为消除场地边界对桩身响应计算结果的影响，桩周土径向计算范围为30 倍桩径，竖向计算范围为3倍桩的埋深，模型及其边界条件设置如图2 所示。图2中，UY为沿Y轴的位移，RX和RZ分别为绕X轴和Z轴的转角。

图1 正、负斜桩示意图Fig.1 Schematic of positive batter pile and negative batter pile

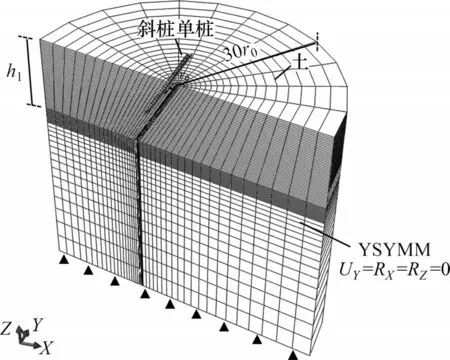
图2 数值模型示意图Fig.2 Schematic of the numerical model

1.2 数值模型验证

数值模拟方法较为广泛地应用于水平受荷桩桩身响应分析，为了保证本文所建立的数值模型能用于分析斜桩单桩基础的水平受荷特性，对数值模型的可靠性进行验证，分别选取水平加载单桩离心模型试验[19]及斜桩水平加载离心模型试验[14]作为验证试验。朱斌等[19]的离心模型试验数值验证模型参数设置为：桩为管桩，桩径为2.5 m，桩长为65 m，壁厚为45 mm，埋深为50 m，桩身弹性模量为210 GPa，泊松比为0.15，桩周土内摩擦角为38°，剪胀角为3°，泊松比为0.3，黏聚力为0.1 kPa。单桩离心模型试验和数值模拟结果对比如图3所示。

ZHANG 等[14]的斜桩单桩离心模型试验数值验证模型参数设置如下：桩为方桩，边长为0.43 m，桩身长度为13.7 m，埋深为10.9 m，桩身弹性模量为73 GPa，泊松比为0.2，桩周土内摩擦角为37°，剪胀角为2°，黏聚力为0.1 kPa，其中负斜桩倾斜角为14°，单桩离心模型试验结果和数值模拟结果对比如图4所示。

从图3和图4可知，数值模拟在分析竖直桩和斜桩单桩水平承载力以及桩身变形特性方面都和离心模型试验结果吻合较好，说明本文建立的数值模型在分析水平荷载作用下桩身承载特性方面具有较强的可靠性，能够在较大程度上反映实际工程中桩身的真实响应。

图3 竖直单桩数值模拟和离心模型试验结果对比Fig.3 Comparison of centrifuge model tests results and FEM results of single vertical pile

图4 斜桩单桩数值模拟和离心模型试验结果对比Fig.4 Comparison of centrifuge model tests results and FEM results of single batter pile

2 正、负斜桩单桩水平承载特性

为了便于分析，数值模型桩-土参数设置如表1和表2所示。

表1 单桩计算参数Table 1 Parameters of single pile

表2 砂土计算参数Table 2 Parameters of sand

2.1 斜桩的水平承载力

斜桩倾斜角分别选取10°，15°，20°，25°和30°，为了便于描述，不同倾斜角负斜桩依次简写为N10，N15，N20，N25，N30，正斜桩简写为B10，B15，B20，B25，B30；D，L和Z分别为桩径、桩长、桩身相对地面位置(沿桩身向下为正方向)。承载力均选取桩顶处位移达到0.1D时对应的水平荷载[20]，并定义斜桩与竖直桩水平承载力的比值为承载比α。不同倾斜角的斜桩荷载-位移曲线如图5所示，表3所示为各倾斜角度下斜桩单桩的承载比α。

图5 斜桩单桩荷载-位移曲线Fig.5 Horizontal load-displacement curves of single batter pile

图5 与表3 的结果表明，相较于竖直桩而言，负斜桩的水平承载力有所提升，而正斜桩的水平承载力则降低，且桩身倾斜角越大，斜桩单桩的水平承载力提升或者减小的幅度越大。

表3 斜桩单桩水平承载力及承载比αTable 3 Horizontal bearing capacity and bearing ratio α of single batter pile

为了进一步研究相较于竖直桩而言斜桩单桩水平承载力变化的机理，分别提取了B30、竖直桩、N30 桩在400 kN 的水平荷载作用下桩周土的位移场，结果如图6所示。

从图6可以看出，斜桩和竖直桩的桩周土位移区的范围不同，在相同水平荷载作用下，无论是在加载方向还是沿桩身方向，正斜桩对桩周土的影响范围均比竖直桩的大，负斜桩对桩周土的影响范围最小。在水平荷载作用下，桩身将荷载传递至桩侧土，桩侧土能提供的水平抵抗力取决于桩侧土滑动面(如图6中虚线所示)提供的阻力，从图6可以看出，当桩侧土位移区面积相同时，负斜桩桩侧土能提供的滑移面的长度显著比竖直桩的大，正斜桩的最小。因此，负斜桩具有更大的水平承载力。

图6 400 kN水平荷载作用下桩周土位移场Fig.6 Displacement field of soil around pile under 400 kN horizontal load

2.2 斜桩的桩身响应

对于实际工程设计而言，人们所关注的不仅是承载力，水平荷载作用下桩身的弯矩、剪力等参数关乎桩身的截面设计，对工程设计具有至关重要的作用。

斜桩的桩身位移随桩身深度变化反映了桩对于桩周土的扰动程度。图7所示为B20桩、竖直桩及N20 桩在不同的水平荷载作用下桩身位移沿桩身深度变化趋势。

从图7可见，随着水平荷载的增加，无论是正斜桩、竖直桩还是负斜桩，桩身位移发展区沿桩身深度范围不会发生显著变化，B20桩的位移发展区主要集中在0～4.5D沿桩身深度范围内，而竖直桩和N20 桩主要位移发展区范围均为0～4D；B20桩和竖直桩桩身反弯区沿桩身深度范围均达到了3.5D，而N20 桩则为3D。综合来看，相较于竖直桩，正斜桩位移发展区沿桩身深度范围较大，反弯区沿桩身深度范围基本一致，而负斜桩位移发展区沿桩身深度范围与竖直桩的相近，而反弯区沿桩身深度范围较小。

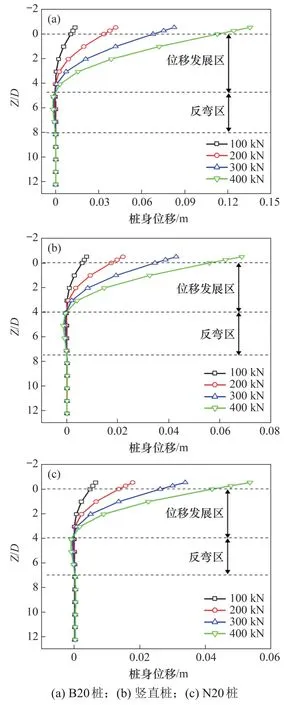
图7 不同水平荷载作用下桩身位移Fig.7 Horizontal displacement of pile under different horizontal loads

为了分析斜桩单桩的桩-土荷载传递性能，进一步提取B20桩、竖直桩及N20桩被动区与主动区的桩-土接触应力，结果如图8所示。

基于主动区和被动区的桩-土接触应力，将桩沿深度分为4 个区，I 区为主要土抗力提供区，在该区域内，被动区的桩-土接触应力明显比主动区的大，此时桩身将大部分的水平荷载传递到周围土体；II区为反弯区，此时桩身产生反弯现象，导致主动区桩-土接触应力比被动区的大；III区为二次反弯区，桩身在水平荷载作用下产生二次反弯现象，导致被动区土抗力比主动区的略大；III 区以下区域为未扰动区，此范围内桩身基本不产生位移，桩-土接触应力和初始土压力相等。从图8可知，在I 区范围内，负斜桩的桩-土接触应力均处于较高水平，竖直桩次之，而正斜桩在近地表部分桩周土提供的抗力较小，结合图6所示桩周土塑性区范围可以看出，近地表处负斜桩在水平方向上塑性区范围更大，因此整体上I区所能提供的抗力均处于较高水平，具备优良的桩-土荷载传递性能。

图8 400 kN水平荷载作用下桩-土接触应力Fig.8 Pile-soil contact stress under 400 kN horizontal loads

图9 所示为不同倾斜角斜桩在400 kN 水平荷载作用下沿桩身的弯矩及剪力分布。

图9 400 kN水平荷载作用下桩身弯矩和剪力Fig.9 Bending moment and shear force of pile under 400 kN horizontal load

从图9(a)可以看出，在桩身相同位置，负斜桩的桩身弯矩小于竖直桩的桩身弯矩，正斜桩桩身弯矩最大，结合图7结果分析，负斜桩桩身整体产生的变形较小，因此桩身产生的弯矩较小，而正斜桩则反之。从图9(b)可以看出，在桩顶处加载，桩顶处剪力最大，之后，桩将荷载传递给周围土体，桩身剪力迅速减小到0，而后桩身出现反弯现象，导致桩身剪力逐渐反向增加再减小至0；负斜桩由于优良的桩-土荷载传递性能，因此桩身剪力迅速减小为0，且因为桩身变形较小，反弯现象相较竖直桩和正斜桩而言不明显，因此，桩身反弯段剪力整体较小。

工程设计中一般按照桩身出现的最大弯矩进行桩身截面设计，图10 所示为不同倾斜角斜桩桩身最大弯矩随水平荷载的变化趋势。

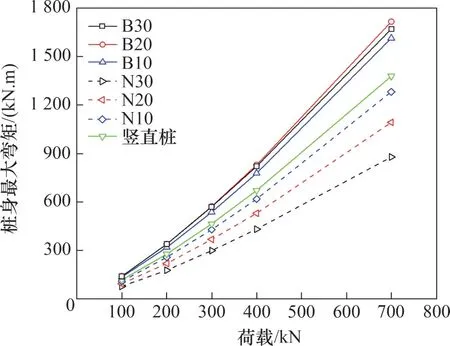
图10 不同水平荷载作用下桩身最大弯矩Fig.10 The largest bending moment along pile shaft under different horizontal loads

从图10 可以看出：随着荷载的增加，桩身最大弯矩大致呈线性增加；对于不同倾斜角的斜桩，桩身最大弯矩-荷载曲线的斜率不同。整体而言，在相同水平荷载作用下，负斜桩的桩身最大弯矩比竖直桩的小，且随倾斜角的逐渐增加而显著减小，而正斜桩的桩身最大弯矩明显比竖直桩的大，但随倾斜角改变的变化不大。从以上分析可以看出，负斜桩单桩相较于竖直桩及正斜桩单桩而言，其具备更大的水平承载力和优良的水平承载特性。因此，在实际工程中，已知水平荷载主要作用方向时，尽量采用负斜桩；当水平荷载作用方向多变时，尽量采用竖直桩基础，以免出现正斜桩受荷情形。

进一步地，将相同水平荷载作用下斜桩桩身最大弯矩与竖直桩桩身最大弯矩的比值定义为弯矩比β，则斜桩桩身最大弯矩可以按式(1)进行计算：

式中：Mv为竖直桩桩身最大弯矩。

图11 所示为不同倾斜角斜桩在不同水平荷载作用下的弯矩比β。

图11 不同倾斜角斜桩弯矩比β取值Fig.11 Value of β under different batter angles of batter piles

从图11 可以看出：对于斜桩而言，当倾斜角度一定时，随着水平荷载的改变，弯矩比β基本上不会发生变化，也就是说弯矩比β几乎不受水平荷载的影响。在实际工程中，斜桩桩身承受的最大弯矩可以按照竖直桩桩身最大弯矩Mv及弯矩比β进行经验取值。

3 斜桩在水平斜交荷载下的承载力

在实际工程中，斜桩基础会受到各个方向水平荷载的作用，水平斜交荷载作用下的斜桩水平承载力如图12所示。

图12 水平斜交荷载示意图Fig.12 Schematic of horizontal oblique load

将水平荷载方向与正斜桩加载方向夹角定义为加载角δ，负斜桩即对应加载角δ为180°时的情形。图13 所示为不同倾斜角度和加载角度下斜桩单桩的承载比α。

从图13 可以看出，随着加载角度的增加，斜桩单桩的水平承载比呈指数曲线样式增加，且斜桩单桩的倾斜角越大，这种增加趋势越明显。在加载角约为130°时，斜桩单桩的水平承载力与竖直桩的水平承载力相当。

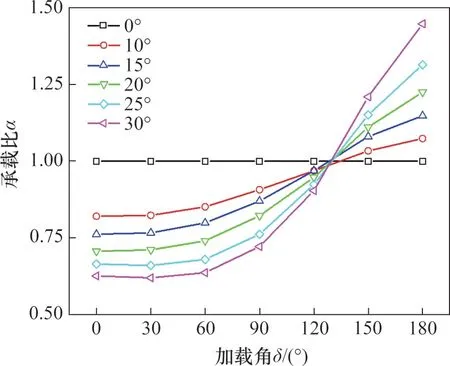
图13 不同加载角度时斜桩的承载比αFig.13 Value of α under different horizontal loading angles

由以上分析可以看出，斜桩的水平承载力和倾斜角以及加载角密切相关，而斜桩的承载比α与加载角δ大致呈指数曲线关系，拟合结果如图14(a)所示。基于对斜桩承载比α与加载角δ关系的拟合，斜桩水平承载比α的经验预测公式如式(2)所示：

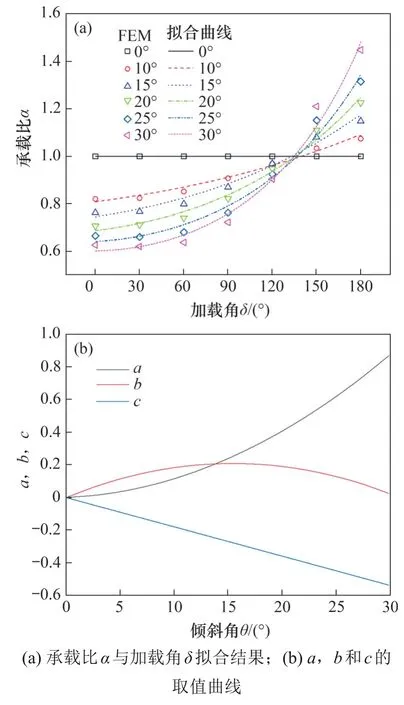
图14 承载比α-加载角δ曲线拟合结果Fig.14 Fitting results of bearing ratio α-horizontal loading angle δ curves

图14(b)所示为30°倾斜角范围内经验系数a，b和c的取值曲线。

为了进一步验证所提出经验公式的可靠性，将经验公式预测结果与不同倾斜角度的正、负斜桩离心模型试验结果、数值模拟结果以及现场试验结果进行对比，结果如图15所示。

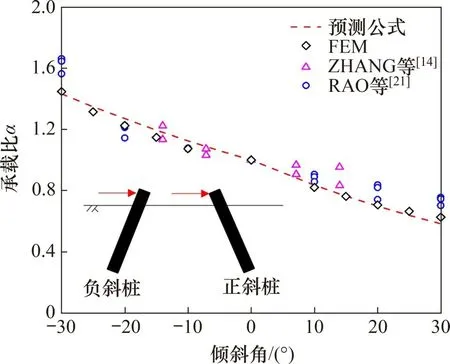
图15 经验预测公式的验证Fig.15 Verification of Empirical formula

从图15 可知，该经验公式在分析斜桩水平承载力时有一定的可靠度，但是，由于土质存在差异、极限承载力判别标准不一致等，预测结果与相关试验结果存在一定的偏差。

4 结论

1)当斜桩倾斜角在30°范围内时，由于负斜桩桩侧土塑性区范围最广，滑移面长度最大，因此，负斜桩的水平承载力比竖直桩的高，正斜桩的水平承载力最小，且倾斜角度越大，这种趋势越明显。

2)在相同水平荷载作用下，负斜桩桩身位移发展区沿桩身深度范围与竖直桩的相近，正斜桩的较大，而正斜桩反弯区沿桩身深度范围和竖直桩的相近，负斜桩的最小。

3)相较于竖直桩而言，负斜桩的被动区桩-土接触应力整体处于较高水平，正斜桩的被动区桩-土接触应力在近地表部分则较小，且负斜桩桩身整体位移、弯矩、剪力幅值均较小，本文给出的正、负斜桩的最大弯矩比预测公式得出的结果可靠。

4)对于斜桩单桩，承载力随水平加载角度的增加呈指数形式上升，且斜桩倾斜角度越大，上升趋势越明显，本文给出的斜桩单桩水平斜交荷载承载比预测公式具有一定的可靠度。