空间视域下义务教育质量对房价的影响

杨慧　曾进　杨乃　孔凡敏

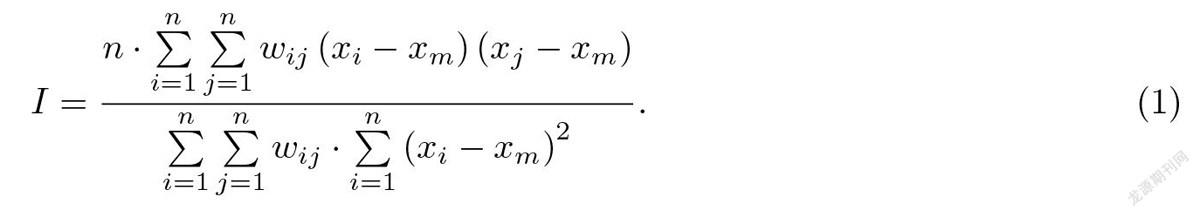
关键词：学区房;教育资源;特征价格模型;GWR模型;教育资本化

中图分类号：K909，F299.23 文献标志码：A DOI：10.3969/j.issn.1000-5641.2022.01.012

0引言

义务教育作为公共服务的主要组成部分，其公平性研究成为多学科交叉研究的热点之一.多篇文献提出我国义务教育呈现不公平性[1-3]，优质义务教育资源的供给短缺和布局不平衡诱导了教育资本化[4].在“就近入学”和教育资源分布不均的背景下，部分家庭愿意支付更高的费用购买优质教育资源周边的住宅[5].在市场化改革、择校紧缩和就近入学的政策背景下，住宅区位成为获取优质教育资源的主要途径[6]，家长根据自己的收入和对义务教育资源的偏好选择居住地区，从而使义务教育资源被资本化为房价[7-10].

国内外关于义务教育资源对房价的影响研究已有一定基础，主要的研究理论为“用脚投票”与教育群分理论和特征价格理论[4].Tiebout[7]提出居民可根据自己对公共产品的消费偏好“用脚投票”去选择居住地.在教育资源分布不均的条件下，拥有优质教育的社区吸引高收入家庭流入，从而推高房价，迫使低收入家庭迁移至拥有劣质教育的社区居住，由此导致基于家庭财富的教育群分现象[4]，进而高收入阶层在质量维度上保持着对贫困阶层的优势[11].特征价格理论源于新消费者理论[12]与隐形市场供需均衡理论[13]，它被广泛运用于城市住宅空间差异的实证分析及住宅价格决定机制的研究[14]，是教育资本化研究的主流方法[15-18].通过保持结构、位置和邻域特征的一致性，利用特征价格模型获得教育变量的隐形贡献[19-20].诸多学者基于特征价格模型定性或定量地评估教育基础设施对房价的影响，其结果表明教育资源对房价具有显著的资本化效应[16，21].

国内关于城市教育质量对房价影响的定量研究呈现以下特点：第一，研究数据多为传统数据源（官方统计数据、人口普查或调查问卷等）.例如，周业安等[22]以2008—2013年北京市出让的396宗居住性质用地为样本，运用特征价格模型研究教育资源对土地价格的影响，结果表明初中地块距离成为影响其价格的重要因素.这类传统数据源制作费用昂贵，更新慢，无法实时获取，且样本数量及其属性无法满足精细尺度空间格局分析的要求[23].当前，在线住房网站已成为住房研究的主要数据来源[23-24]，方便研究人员获取实时住房价格数据和相关地理信息，可揭示住房市场的真实情况[25-27].第二，研究方法多为特征价格模型.例如，张珂等通过特征价格模型的定量化，表明城市基础教育资源对房价具有溢价现象[5].Kim等[28]就学校资源对房价的影响进行估计，结果表明特征价格模型在考虑空间关系之后具有较高的拟合优度，但该模型忽视了城市地价空间异质性[29].Li等[30]将空间异质性定义为系统或系统属性在空间上的复杂性和变异性，地理空间的非均衡性地理结构是空间异质性[31]，这种异质性具体表现为经济行为或经济关系在空间上的不稳定性[32].Fortheringham等[32]和Brunsdon等[33]提出的地理加权回归模型（Geographic Weighted Regression，GWR）成功解决了空间异质性的问题，并证明将其应用于房价研究，结果优于传统特征价格模型.

在此背景下，本研究以武汉市为例，从搜房网、家长帮、武汉市教育局等网站获取房价和学校等数据，采用GWR模型对中小学校质量对房价的影响程度和差异性进行量化，重新审视公共教育服务的均衡性问题.

1研究区域

武汉是我国重要的工业、科教基地和综合交通枢纽[34]，也是2014年开始落实就近入学政策的重点城市之一[35].武汉市经济高质量发展主要指标居全国同类城市前列，经济保持平稳较快增长[36]，2019年房地产开发投资比上年增长3.5%，其中住宅投资增长6.3%[37].故以武汉市为研究对象，探究其义务教育对房价的影响具有显著意义.

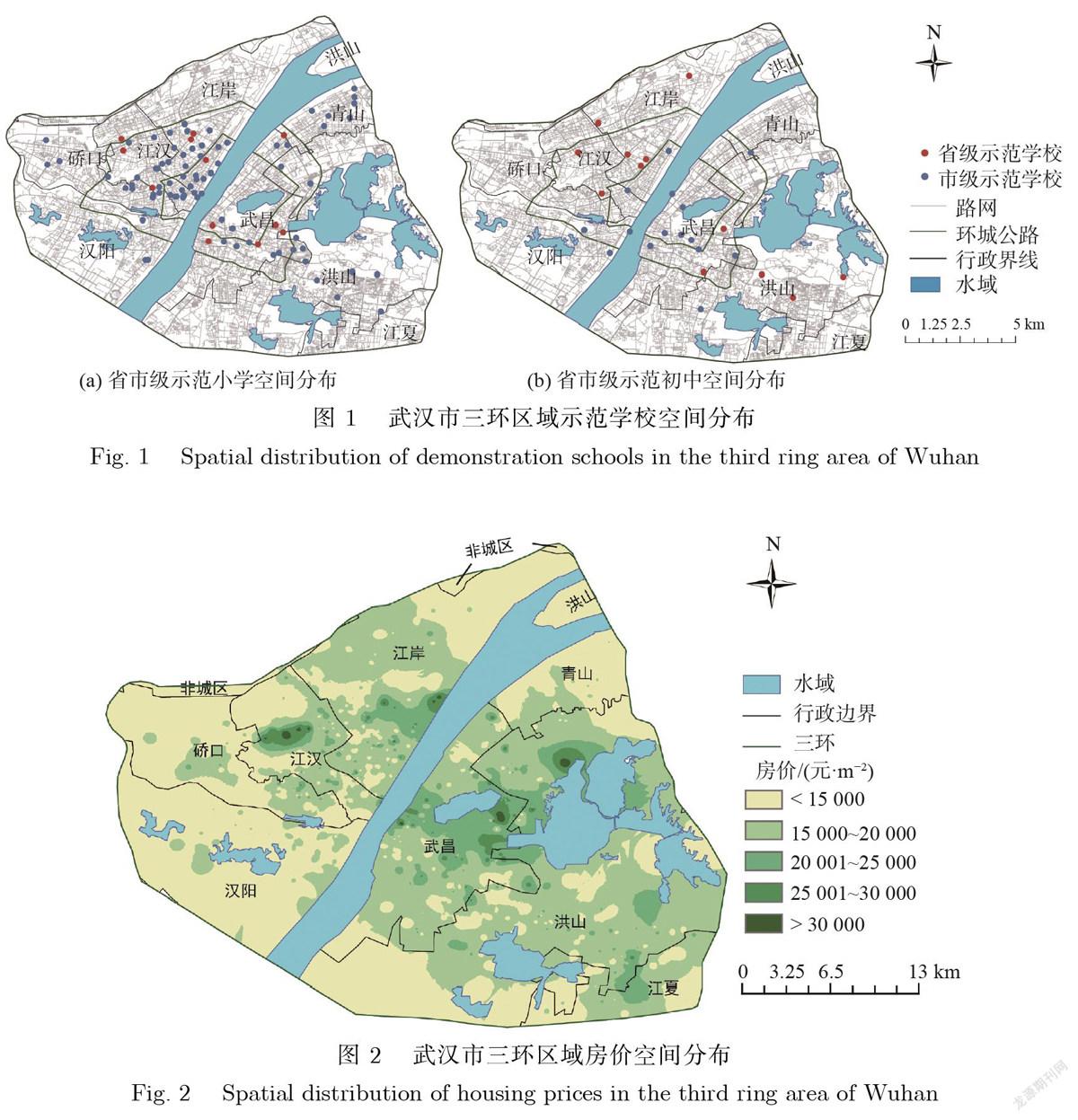
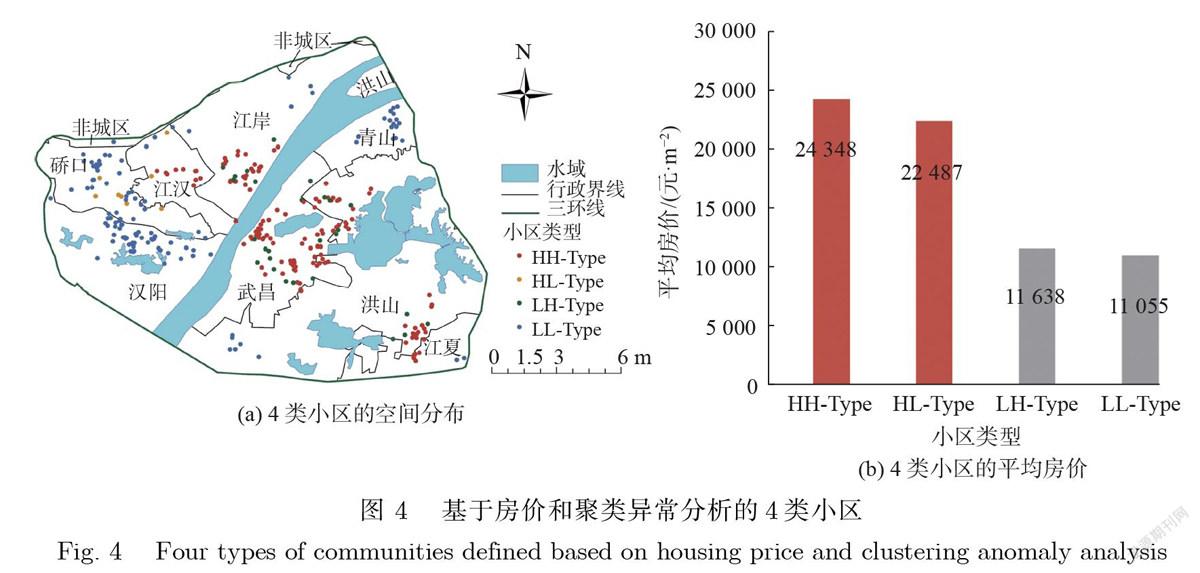
本研究的研究区域为武汉市三环所围成的区域，其数据主要包括以下4个部分：①行政区数据源于湖北省测绘局地理信息网;②武汉市小区数据及其结构特征（即房屋年龄、房屋类别、建筑高度、容积率、绿化率、物业管理费、住户数和停车数等）数据通过搜房网获取，搜房网还提供了小区与小学、小学与初中间的匹配数据;③学校数据可从家长帮和武汉市教育局获取，质量等级主要分为省级学校、市级学校和普通学校3类，前两类也可合称为示范学校;④大学、医院、酒店、商店、地铁的位置数据和武汉交通网数据通过高德地图收集.数据展示如图1、图2所示.

2研究方法

2.1影响变量的设定与量化

房屋由众多不同的特征变量构成（表1），依据当前研究文献[21，23，38]可知，中小学教育对房价的影响因素主要分为4类：区位、建筑结构、邻里环境和教育资源特征.为避免回归分析过程中的共线性问题，需减少使用二值化变量或空值.各变量的具体量化方法如表2所示.

其中，学校质量通常使用投入数据（教师工资、学生支出[39]和师生比等）或产出数据（考试分数[40]、辍学率[41]等）来衡量，但这类数据较少公开.由于官方或非官方学校排名也可为学校教育质量好坏提供参考，故本研究以此作为判断学校质量的标准.

2.2空间自相关

为满足GWR应用前提，本研究引入空间相关性分析模型，用以验证房价的空间异质性或空间非平稳性.局部Moran’sI指数是度量某一栅格单元与相邻栅格单元空间自相关程度的常用指标[43]，因此，本研究选择局部Moran’sI指数用以分析小区房价的空间相关性，其公式[43]为

2.3GWR模型

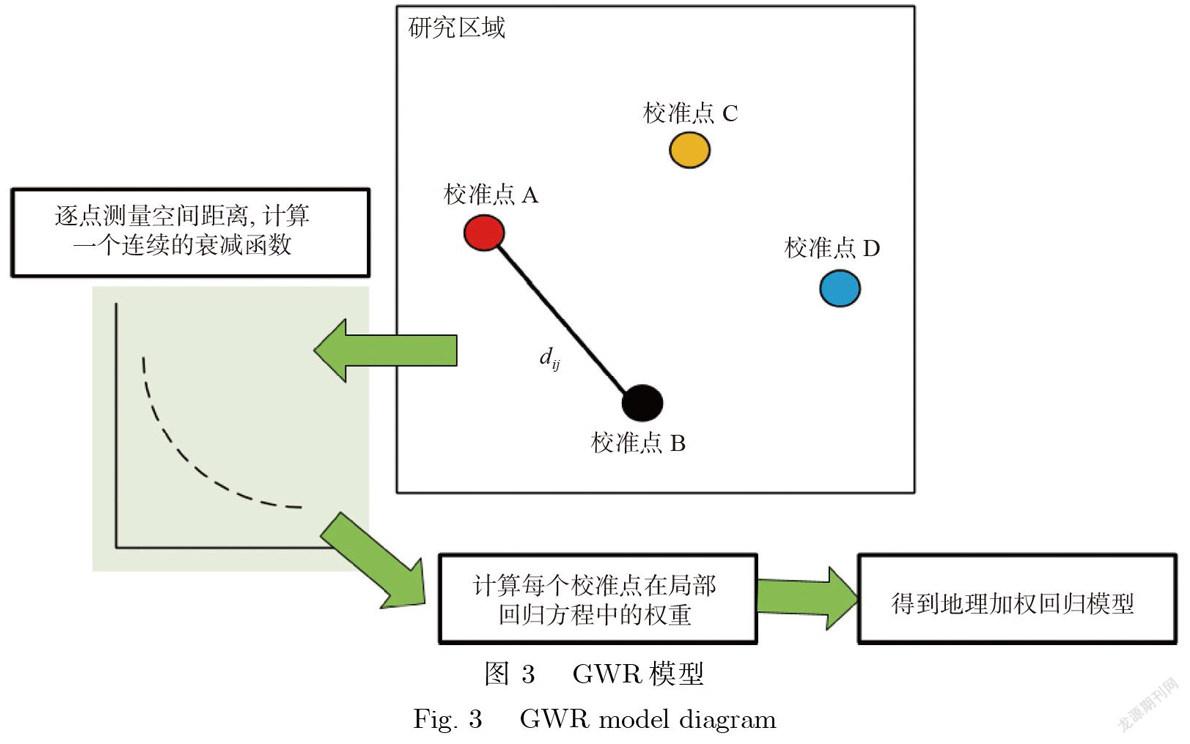
GWR模型是对简单线性回归模型的扩展[44]，用于研究回归模型中变量间的关系在空间上的变化潜力[45]，其在回归分析时加入了地理位置信息，适用于具有空间非平稳性的数据[46].GWR模型利用了局部加权回归中的非参数计算方法，通过空间中估计点附近的数据子集估计该点的局部回归参数.GWR模型的创新之处在于使用了校准点（单个数据点或面的质心）在地理空间附近的数据集（图3），而非变量空间.它作为对空间变化关系进行推断的方法，重点从原来的预测因变量扩展到验证分析[47].相比传统特征价格模型，GWR模型適用于变量间的关系在研究区域内变化的情况.

地理加权回归模型的基本思路是在一个研究范围内，利用校准点的地理位置，逐点测量与周围校准点的空间距离，计算出一个连续的衰减函数.再将每个要素的观测值代入衰减函数，计算出每个要素在局部回归方程中的权重.最后得出加权回归方程，如图3所示.

GWR模型给数据集中每个要素建立一个拟合回归.校准点的空间坐标用于点间距离计算，校准过程中，点间距离较小的要素相比较大的要素将赋予更高的权重.对于校准位置i=1，…n，GWR模型[48-49]可表示为

2.4空间核函数与带宽的确定

针对式（2）GWR模型，对每个回归分析点i分别采用加权线性最小二乘法进行模型求解[49]，可得

其中，对角线w（j=1，2…，n）表示第j个数据点到回归分析点i的权重值.同时，在值域[0，1]内，关于空间距离的单调减函数的权重计算，称之为核函数[50-51]，即GWR中局部权重矩阵W根据核函数计算得出.核函数计算基本原则：某点距离校准位置越近，则赋予该点的权重越大，反之则权重越小.固定高斯函数、固定双重平方函数、调整双重平方函数和调整高斯函数为常用的4种核函数[52]，具体公式见表3.根据具体研究的数据与模型，选择最为合适的核函数，可确保研究的科学性和可行性.

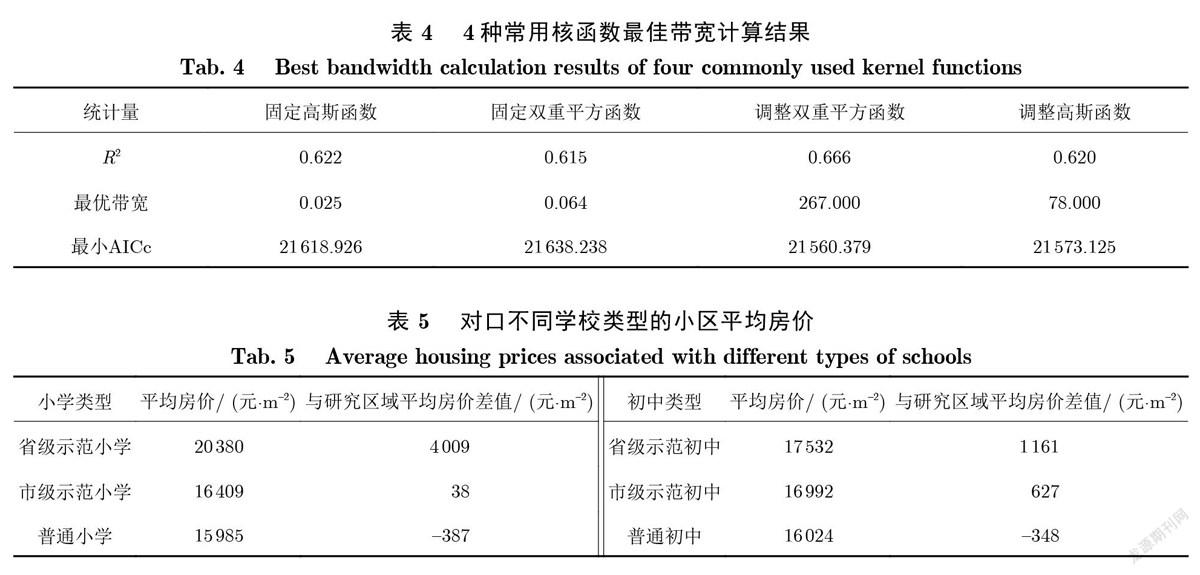
带宽是GWR模型权重计算的重要控制参数，可分为固定型和可变型带宽[49].在求解GWR模型时，可通过交叉验证（Cross Validation，CV）[53]或赤池信息量准则（Akaike Information Criterion，AIC）[54]对带宽值进行优选.AICc（CorrectedAIC）表示校正AIC值[43]，且AICc值相对于CV优化程度好[49]，故本研究选择AICc确定最优带宽.基于GWR4.0软件平台，选择AICc确定最优带宽，计算4种核函数的相关参数，根据最小AICc准则[48，55]（AICc越小越好），确定调整双重平方函数为本研究核函数（表4）.

3结果分析

3.1义务教育对房价的空间分异特征

研究区域平均房价为16371元/m，其中省级示范学校对口小区的平均房价最高，市级示范小学次之，普通学校最低（表5），表明示范学校和普通学校对房价的影响存在差异性.同时，通过各类学校对口小区的平均房价与总样本平均房价的差值，可粗略地反映示范学校的额外价值，但样本的位置和邻域特征没有得到充分的控制.

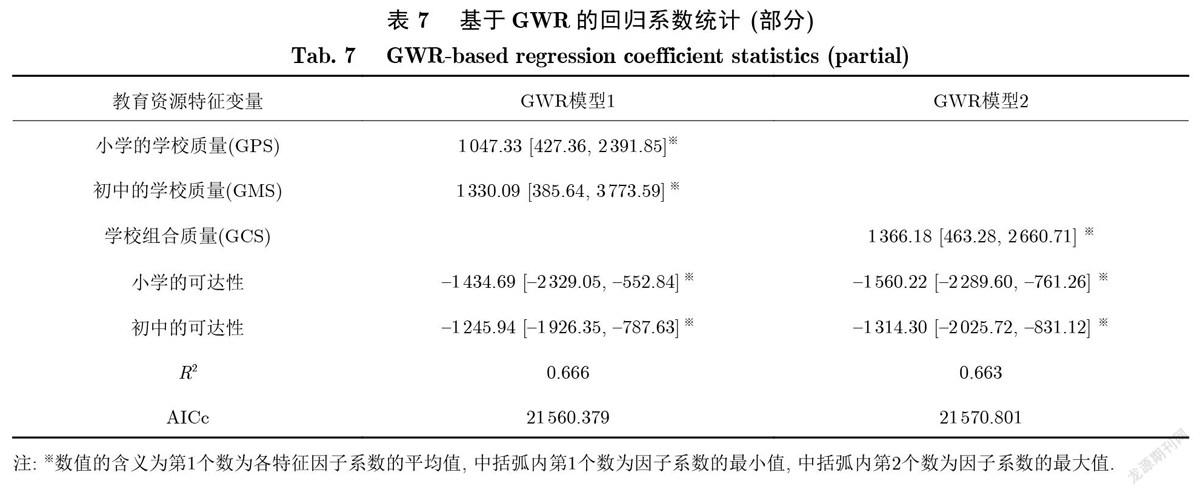
使用ArcGIS中“聚类和异常值分析”（Anselin Local Morans’I）工具对小区房价进行统计分析，得到以下4类点数据：热点（房价高值的空间聚类，HH，红点）、冷点（房价低值的空间聚类，LL，蓝点）、被低值房价包围的高值房价点（HL，橙点）和被高值房价包围的低值房价点（LH，绿点），见图4（a）.其中，HH-Type小区主要分布于市区中心以及洪山区和江夏区的交界处;LH-Type小区夹杂于HH-Type小区内，空间分布与HH-Type小区相似;LL-Type小区主要分布于汉阳和硚口区以及青山区青山公园附近;HL-Type小区较少，分布于江汉武商商务区附近.局部Moran’sI指数反映局部空间自相关，描述一个空间单元与其领域的相似程度，能够表示每个局部单元服从全局总趋势的程度（包括方向和量级），并显示空间异质，说明空间依赖是如何随位置变化的.通过该指标，可分析不同类型房价聚集区的对口学校类型占比，从而探索不同等级房价与不同类型学校之间的关联关系.

在“就近入学”政策的作用下，小区与对口中小学间形成了紧密的关系，故本研究依据表6分别统计以上4类小区的平均房价及对口学校的类型分布，以反映小区拥有义务教育资源的情况.从学校总体类型上可知（图4（b）和图5（a））①HH-Type小区的平均房价最高，其对口学校中示范学校的占比相比其他3类小区有绝对优势;②HH-Type小区和HL-Type小区的平均房价高于其他两类小区，且两者对口学校中省级示范学校占比明显高于其他两类小区;③LH-Type小区和LL-Type小区平均房价基本一致，这两类小区的学校组成占比也基本相同.从中小学类型角度可知（图5（b））：①HHType小区和HL-Type小区的对口省级示范小学占比相比其他兩类小区明显较高;②HH-Type小区和HL-Type小区的对口省级示范初中占比相比其他两类小区明显较高.

从表6组合类型的分类1可知（图5（c））：①HH-Type小区的对口学校组合结构中，至少对口一所示范学校的小区占比明显高于其他小区类型;②HH-Type小区、HL-Type小区和LH-Type小区的对口学校组合中，两所学校均为示范学校的占比基本相同.从表6组合类型的分类2可知（图5（c））：①HL-Type小区的对口学校中两所均为省级示范学校的占比最高，其次是HH-Type小区;②HHType小区、HL-Type小区和LH-Type小区的对口学校中，一省级示范加一市级示范的组合占比基本相同.

综上可知，当小区对口示范学校时，房价会有相应的提高，尤其当对口省级示范学校时，房价提高程度相对较大.从统计学角度看出，义务教育质量对房价具有正相关影响，其省级示范学校对房价的溢价程度相对较高.

3.2学校质量对房价的影响

本研究主要生成两个模型，模型1用以研究对口中小学的学校质量和可达性对房价影响，模型2用以研究对口学校组合质量对房价的影响.

根据第2节的GWR研究方法进行计算（表7和表8），结果表明：①GWR模型整体上可以解释研究范围内房价总变异的66%左右.②模型拟合残差的莫兰指数显示非显著，表明GWR成功解决了残差自相关问题.③所有解释变量的方差膨胀系数（Variance Inflation Factor，VIF，解释变量间的冗余）均小于3.4，表明模型中解释变量之间不存在比较严重的共线性.④学校质量对房价具有正相关关系，小学等级每提高一个等级（即对口学校的等级从“普通学校”上升为“市级示范学校”或从“市级示范学校”上升为“省级示范学校”），其对口的小区房价将平均提高1047元/m，最高可提高2392元/m，最低可提高427元/m2;初中等级每提高一个等级，其对口的小区房价将平均提高1330元/m，最高可提高3773.59元/m，最低可提高385.64元/m.综上，初中质量对房价的影响大于小学，即初中质量的资本化效应高于小学.本研究认为原因如下：相比小升初100%升学率的义务教育升学，初升高的竞争则要严峻得多，“普中”招生规模和复读等政策的改变深刻影响着孩子的中考成绩[56].因此，一些家长更看重初中的学校质量，购房时会更偏向初中对口学区房.

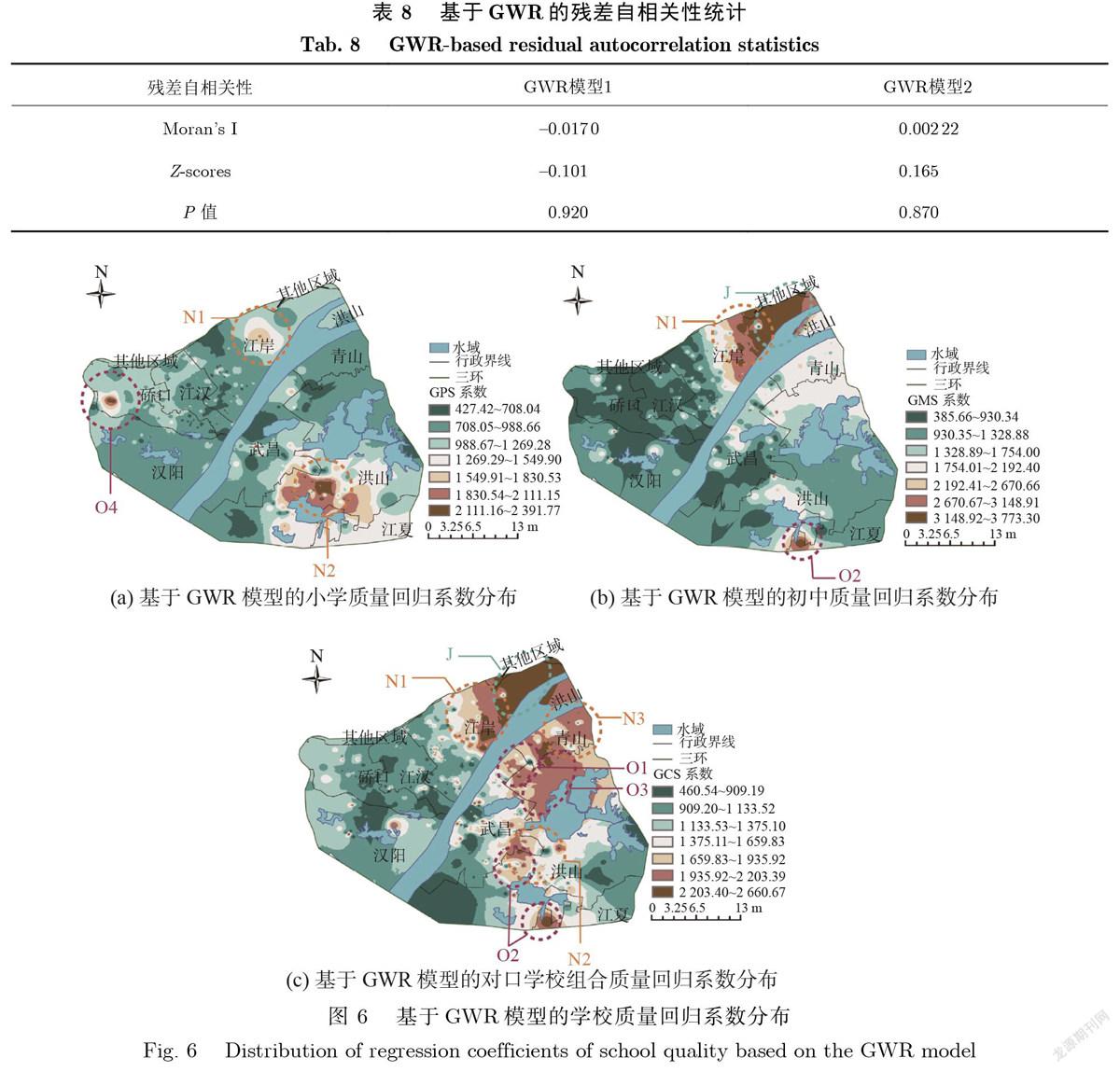
运用反距离权重插值法，对GWR分析结果进行可视化，其系数越高，代表学校质量对房价的影响程度越高，如图6所示：①以后湖（N1区）、光谷（N2区）等片区为代表的新城区相较于老城区中硚口区古田一带（O4区）的小学教育质量对房价的影响更大（图6（a））;②以后湖（N1区）等片区为代表的新城区和江岸区中部及北部区域（J区）相较于老城区中二环线沿线的洪山区南湖片区（O2区）的初中教育质量对房价的影响较大（图6（b））;③地处城市内环线沿线的徐东片区（O1区）、二环线沿线的洪山区南湖片区（O2区）、和平片区和铁机片区（O3区）的老城区，以后湖（N1区）和光谷（N2区）以及三环沿线内青山区（N3区）为代表的新城区，还包括江岸区中部及北部区域（J区）的对口学校组合质量对房价的影响较大，但江岸区的影响最大（图6（c））;④武昌区、硚口区和江汉区整体上学校质量对房价影响较小.

其影响原因如下：一是因新城区中小学教育资源配套不足和其城市发展速度不匹配的问题，逐渐形成教育“洼地”，供需矛盾日益突出.教育资源不足的问题使得优质教育资源成为家长们争相追逐的对象，学校等级的提升会引起房价较大的变动.二是因城中村改造滞后、历史遗留等原因，使得老城区内的黄金宝地也“塌陷”成教育“洼地”.三是因为江岸区是湖北省课程改革实验区，其内部教育资源分布并不均衡.如江岸区后湖片区，由于近年来的快速发展，入住人口激增，学校配件步伐暂未跟上，适龄儿童上学成为难题，再者，江岸区房价在全市范围较高，该区二手房均价在武汉市排名第二，仅次于武昌区，故其义务教育学校对房价的影响最大.四是因为武昌区作为国家级课程改革实验区、硚口和江汉区是省级课改实验区和硚口区是全省教育资源均衡先进区的原因，该区教育资源丰富，尤其是优质教育资源，因而义务教育学校质量的提升对当地房价的影响相对较小.

4总结

本研究运用聚类分析和数理统计方法，探讨了公立学校质量与房价之间可能存在的关系，且使用GWR模型研究了两者间的关系.结果表明：①义务教育质量与房价存在正相关关系，其省级示范学校对房价的溢价程度相对较高;②初中质量的资本化效应会高于小学;③新城区区域的中小学教育质量对房价的影响较大，江岸区中部及北部区域的对口学校组合质量对房价影响最大，武昌区、硚口区和江汉区整体上学校质量对房价影响较小.

本文研究结论对制定相关教育政策具有参考意义.例如，教育行政部门在实施“就近入学”政策的过程中，要充分考虑到優质教育资源的资本化效应，以及由此产生的“学区房”问题.努力缩小市域内校际差距，在推动义务教育优质均衡发展的前提下，公平分配教育机会.同时，在新城区建设和老旧小区改造的过程中，注重住房与公共服务设施协同规划，特别是根据辖区内学龄人口的变化，优化义务教育资源配置.

限于数据获取的局限性，本研究的房价数据不具备时序性，未考虑时空数据的非平稳性问题，并且在特征影响因子的选择上，未考虑政策制度和房屋内部特征因子对房价的影响.因此，在进一步的研究工作中可纳入以上不足，以期获得更为准确的研究结果.

（责任编辑：李万会）