基于自编游戏情境的初中数学教学设计与反思

张佳萍

[摘  要] “最短路径问题”是各版本教材着力强调的重点，也是中考考查的热点，笔者以自编游戏情境的形式演绎“最短路径问题”，激发学生的内驱力，通过动手、动口、动脑培养学生的动手操作能力、合作互动能力与数学建模能力.

[关键词] 自编;游戏情境;最短路径;初中数学

“最短路径问题”是各版本教材着力强调的重点，也是中考考查的热点，其以“将军饮马”问题为经典模型，主要考查线段公理及轴对称性质，常表现为求线段和的最小值. 教学中，教师虽着力分析与强调，但学生每遇此种类型题，总是一头雾水，不知从何入手. 为了突破这个教学重难点，笔者以自编游戏情境的形式演绎“最短路径问题”，激发学生的内驱力，通过动手操作、小组合作实现问题的突破.

基于游戏情境的教学设计

环节1  经典永流传.

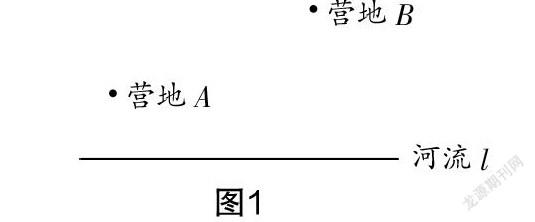
“将军饮马”的故事：海伦是亚历山大城里一位有名的学者. 有一天，一位将军去拜访海伦，想请海伦解答一个令这位将军百思不得其解的问题：将军每天从图1中的营地A出发，到河流l（直线l）饮马后再到营地B，那么将军应在河流的什么地点饮马，所走的路程才能最短呢？[1]

设计意图  首先介绍“将军饮马问题”的出处，给学生以历史的真实感，以著名学者海伦解决“最短路径问题”引起学生重视，激起学生的学习欲望和学习兴趣.

环节2  自编游戏情境——悟空降妖除魔.

科学家爱因斯坦曾言：“兴趣是最好的老师.”一个人只有对一件事产生了兴趣，才会自主去探究与发现，且在探索求知的过程中，他的情绪是愉悦的，学习的效果也是最佳的.

游戏背景：话说唐僧师徒四人去西天取经，一路上披荆斩棘，降妖除魔，为了取得真经可以说历尽艰险，上演了一段段英雄传奇的故事.

设计意图  通过学生耳熟能详的《西游记》让其在感受中华传统文化的同时，自然进入本节课学习的重难点，把本节课的各类问题置于闯关游戏中，游戏关卡由浅入深，不断递进.

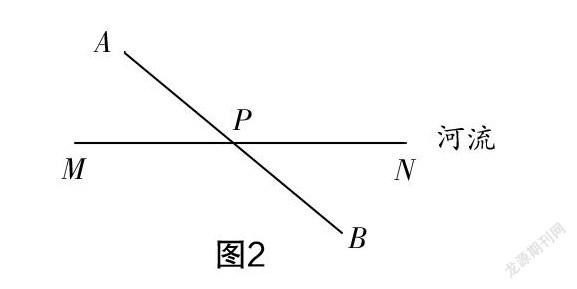
第一关：唐僧师徒四人来到黄风岭，在河流的下游A处休息时下起了暴雨，河水涨得很快，他们应尽快到对岸河流上游的B地才能躲避险情，走怎样的路線才能最节省时间呢？（最短路线的设计如图2所示）

设计意图  此类问题是“最短路径问题”中最简单的一类，只需应用线段公理“两点之间，线段最短”就可以解决问题. 学生由此经历了从实际问题到数学问题的一小步，为下面继续闯关提供了理论支撑.

第二关：唐僧师徒四人到五庄观投宿，猪八戒引诱孙悟空去偷来人参果，师兄弟一起分享. 道童发现人参果少了几个，怒骂唐僧师徒四人，孙悟空怒不可遏，把人参果树推倒. 趁着夜色师徒四人匆匆逃逸，镇元大仙用法术将他们捉了回去. 镇元大仙声称，如果孙悟空能够解决“将军饮马问题”，就放他们师徒四人走.

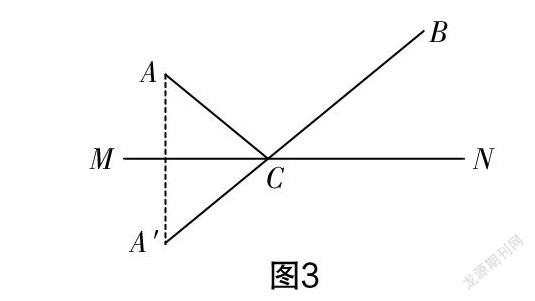
设计意图  让经典故事在第二关中重现，一方面是学生必须解决这个经典问题才能解决其他问题，另一方面是突出本节课的重点——引导学生如何将实际问题转化为数学问题，强化学生的转化能力. 学生帮助孙悟空从中抽象出的数学模型如下：在固定直线MN的同侧有两个固定点A，B，在直线MN上求作一点C，使AC+BC最小. 解决方法为：作点A的对称点A′，连接A′B与直线MN的交点C就是所求作的点. 如图3所示.

第三关：唐僧无意中闯进了黄袍怪的洞府. 黄袍怪的夫人原是宝象国公主百花羞，十三年前被掳进波月洞. 她悄悄放走了唐僧，请他给父王送信. 为了让父王相信师徒四人，百花羞把“将马饮马问题”的证明过程交给了师徒四人，作为他们见面时的信物：

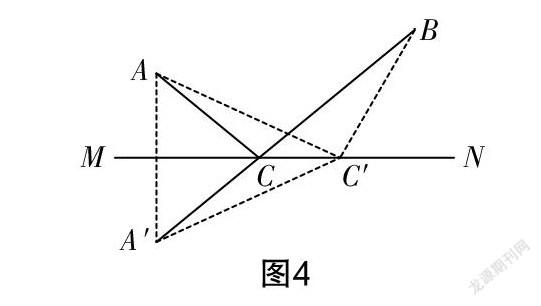
如图4所示，在直线MN上取一点不同于点C的点C′，分别连接AC′，BC′，A′C′. 由轴对称的性质，得AC=A′C，AC′=A′C′，这样AC+BC转化为A′C+BC，即转化为A′B，且AC′+BC′转化为A′C′+BC′. 因为在△A′C′B中，根据三角形的三边关系，得A′B< A′C′+BC′，所以AC+BC最小.

设计意图  学生掌握数学模型仅是“知其然”，还应“知其所以然”. 通过证明这种作图方法的正确性，才能让学生信服，从而进一步理解这种作图方法的深层含义，即利用轴对称的性质用点A的对称点将其代替，从而实现“化折为直”的目的.

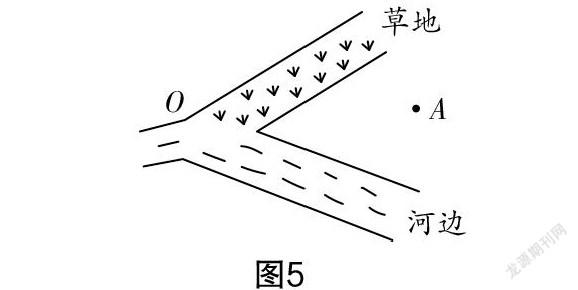
第四关：祭赛国金光寺几年前一阵血雨过后，寺中塔顶的舍利子佛宝无影无踪. 僧人们被罚受苦，沉冤难雪. 为查失宝，悟空携八戒入碧波潭，先礼后兵，与龙王之女乃圣公主及九头虫驸马交战. 白龙马化做少年，入潭寻见乃圣公主，设计骗回佛宝. 如图5所示，为了犒劳白龙马，决定让白龙马从A地出发到草地吃草，再到河边饮水，最后再回到点A，白龙马如何走路径最短？

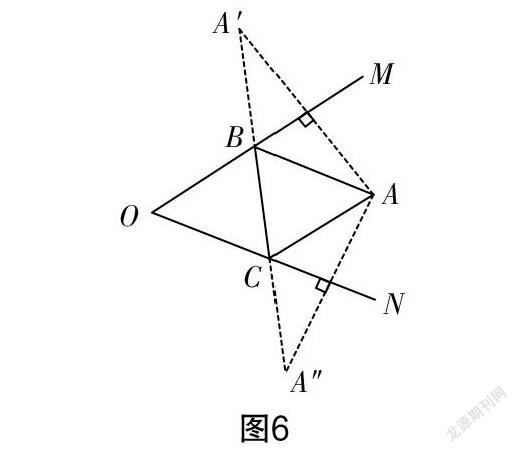
作图过程如图6所示，分别作点A关于直线OM，ON的对称点A′，A″，连接A′A″，与OM，ON的交点（点B，C）就是所求作的点.

设计意图  解决第四关游戏问题是知识的再迁移：第三关游戏问题作一次轴对称即可解决，而第四关游戏问题则需要作两次轴对称才可以解决. 实际上解决的是在角的内部作一个周长最小的三角形的问题，开阔了学生的视野，提升了学生的思维水平.

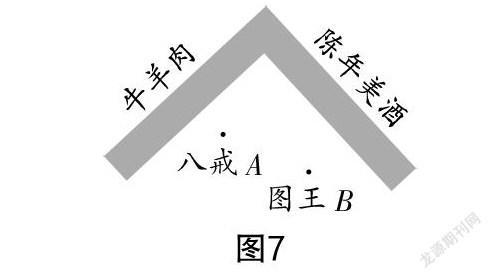
第五关：玉华州国王下旨逐僧出境. 唐僧师徒四人来到州境，适逢三个太子领兵盘查，四人分别躲进米缸、衣箱、席筒、木柜内，被抬进宫去听候发落. 夜间，悟空用隐身术潜入宫中，作法把国王、王后、妃嫔等满朝文武顶上头发全部剃光. 国王很受教训，忏悔排佛不对，礼遇唐僧师徒. 为感谢师徒四人对自己的成功劝谏，设宴款待师徒四人. 如图7所示，宴席上，在A处的八戒准备先去取一块牛肉，再去取一坛美酒，向国王敬上一杯酒后回到自己的位置，八戒如何走路径最短？

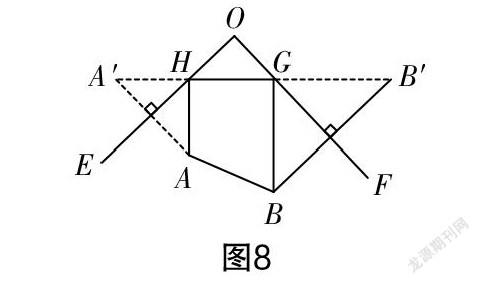
作图过程如图8所示，作点A关于OE的对称点A′，作点B关于OF的对称点B′，连接A′B′，与OE，OF的交点（点H，G）就是所求作的点.

设计意图  第五关游戏问题虽然也是通过作轴对称解决的，但与第四关游戏问题不同的是，这里在一个角的内部有两个固定点，实际上解决的是在角的内部求作一个周长最小的四边形的问题. 通过以上问题的解决，学生能够明白：解决“最短路径问题”就是解决“轴对称问题”，其关键是找准固定点和固定直线，继而作出对称点.

基于游戏情境的教学反思

本节课的设计主线是“实际生活问题—数学知识问题—解决数学问题—解决生活问题”[2]. 在数学课堂教学中，笔者先通过数学建模引导学生把生活问题转化为数学问题，接着用数学知识解决数学问题，最后运用数学问题的结论去审视生活问题，从而有效提高学生的应用意识.

教学设计中，教师要学会处理和加工教材，创设出学生易于接受的形式多样的教学情境，才能突出重点、突破难点[3]. 本节课通过《西游记》的故事让学生感受中华传统文化的同时，学会如何解决“最短路径问题”，体现了由简单到复杂、由浅入深的教学进程.

本节课以学生自主探索为主，采用了情境教学与任务驱动法，在教学过程中，辅以学习小组的合作互动，通过动手、动口、动脑，锻炼学生的动手操作能力、合作互动能力与数学建模能力.

参考文献：

[1]丁力. 初中数学几何最值问题探究——以“将军饮马”问题模型的解题策略为例[J]. 数学教学通讯，2020（14）：79-80.

[2]杜庆术. 数学游戏在初中数学教学中的应用[J]. 中学数学，2019（22）：92-93.

[3]张伟俊. “综合与实践”课的教学探索与实施建议——以“探究最短路径问题”为例[J]. 中国数学教育，2015（11）：11-14.