隔震结构复振型分解反应谱方法研究

2022-03-27陈华霆李晓磊

振动与冲击 2022年6期

杨奎，谭平，陈华霆，李晓磊

(1. 广州大学广东省地震工程与应用技术重点实验室，广州 510405；2. 广州大学工程抗震减震与结构安全教育部重点实验室，广州 510405)

隔震结构一般由上部结构和隔震系统组成，由于两者阻尼特性不同，形成了典型的非比例阻尼体系。非比例阻尼特性对隔震结构的动力响应是不可忽略的[1-2]。对于隔震结构设计，按照我国GB 50011—2010《建筑结构抗震设计规范》可采用基于水平向减震系数的分部设计方法，其地震作用计算采用强迫解耦的传统反应谱方法[3]，但没有充分考虑非经典阻尼的影响。由于强迫解耦法缺乏理论依据，所以很多科研人员致力于复模态的研究[4-6]。

Chen等[7]提出了有效的非经典阻尼体系荷载Ritz向量生成算法，进一步提高了计算效率。为了降低计算规模，仅考虑低阶振型参与计算，同时考虑高阶振型影响，陈华霆等[8]提出了复振型加速度方法。上述研究成果为复振型叠加方法向工程应用奠定了基础。Igusa等[9-10]在复模态理论的框架下，假定地震动为平稳白噪声过程，给出了各自的组合规则，但其振型相关系数较为复杂。周锡元等[11]利用复平面围道积分理论推导出了解析形式的振型位移-位移、速度-位移和速度-速度的相关系数，提出了简便的复振型完全平方组合(complex complete quadratic combination，CCQC)组合规则。之后，Yu等[12-13]又将CCQC方法推广到了多维、多点地震输入的情况，Liu等[14]进一步在多点地震输入的反应谱方法中考虑了等效地震荷载中阻尼的影响，Chen等[15]基于模态扩展方法在CCQC中引入了截断的高阶振型贡献。由于复模态分析中，所要求解特征值问题的规模是系统自由度的两倍，限制了复振型叠加方法的应用。因此当前相关科研人员主要从事对其进行优化和扩展应用上，本文将在上述研究的基础上重点讨论阻尼矩阵构造对隔震结构复振型分解反应谱法的影响。

非比例阻尼矩阵的构造是复振型分解反应谱法实施的基础，对其开展相关研究是非常必要的。本文以隔震结构为研究对象，分别以瑞利阻尼、振型叠加阻尼系数和阻尼比换算阻尼系数3种方法，根据隔震结构特点，按照刚度矩阵的集装方式来组装形成4种不同的整体非比例阻尼矩阵。采用两种不同的天然波反应谱，以反应谱CCQC和反应谱完全平方组合(complete quadratic combination，CQC)分析不同阻尼矩阵形成方式对结构响应的影响以及隔震层等效周期、等效阻尼比、地震动特性对CQC和CCQC方法计算精度的影响，最后基于分析结果以设计反应谱CQC和设计反应谱CCQC研究隔震层不同等效周期和等效阻尼比对隔震结构的楼层位移和楼层剪力误差影响。

1 隔震结构运动方程

基础隔震结构计算简图可简化，如图1所示。图1中：mb,kb为隔震层的质量和等效刚度；m1～mn为上部结构各层质量；k1～kn为上部结构各层的刚度；x1～xn为各层相对地面的位移。

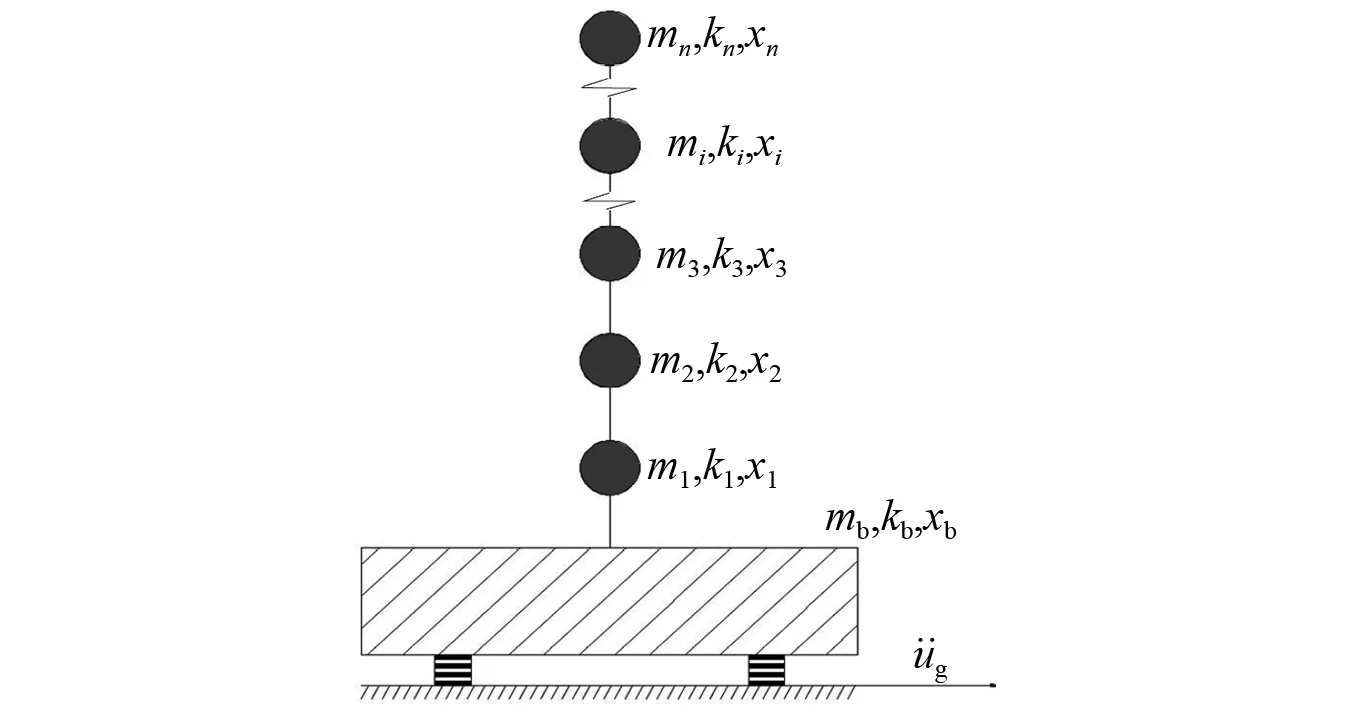
图1 隔震体系模型示意图

针对图1隔震结构运动示意图，以各质点相对地面作为运动变量。该体系在地震作用下的运动方程可表达为

(1)

由于隔震层与上结构材料不同，两者的阻尼有明显差异，所以在其运动方程在振型空间展开具有耦合项，如式(2)所示。

式(1)中x在无阻尼空间Φ展开，即x=Φq，则式(1)可由振型运动方程表示

(2)

2 隔震结构反应谱CCQC法理论

为对式(1)中隔震结构运动方程进行解耦，需要利用Foss变换[16]将其转化为2n个一阶微分方程，即

(3)

矩阵A和B为对称非正定矩阵，利用式(4)可求得结构的特征值和特征向量

(λA+B)ψ=0

(4)

(5)

式中， Re(·)和Im(·)分别为取复数的实部和虚部。

本文利用复振型叠加方法，位移向量x可展开为

(6)

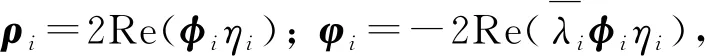
(7)

在工程实践中，通常关心的反应量有层位移、层间位移以及剪力、弯矩等，这些反应量是与位移相关的，故任意地震反应量R(t)=νTx(t)，ν为响应转换向量，与结构的几何、物理属性有关。利用式(6)，R(t)可进一步表示为

(8)

式中：αi=νTρi；βi=νTφi。

(9)

式中，Vi与Di分别为第i阶振型对应的速度谱值和位移谱值，为了使用的方便，通常速度谱由伪速度谱代替；ρvv,ij、ρvd,ij和ρdd,ij分别为振型速度-速度、速度-位移和位移-位移的振型相关系数，具有以下表达形式

(r=ωi/ωj)

(10)

(11)

(12)

式(7)即在一维地震作用下CCQC的表达形式，在引入相应的假定后可以将其进一步推广到多维、多点地震激励作用的情况。不过上述是基于线性系统推导而来，对于隔震结构需要提供隔震支座等效刚度，可以通过迭代确定。迭代步骤可详见文献[19]，如图2所示。一般初始迭代位移在设防地震、罕遇地震作用下分别取100%、250%剪应变对应的位移值。

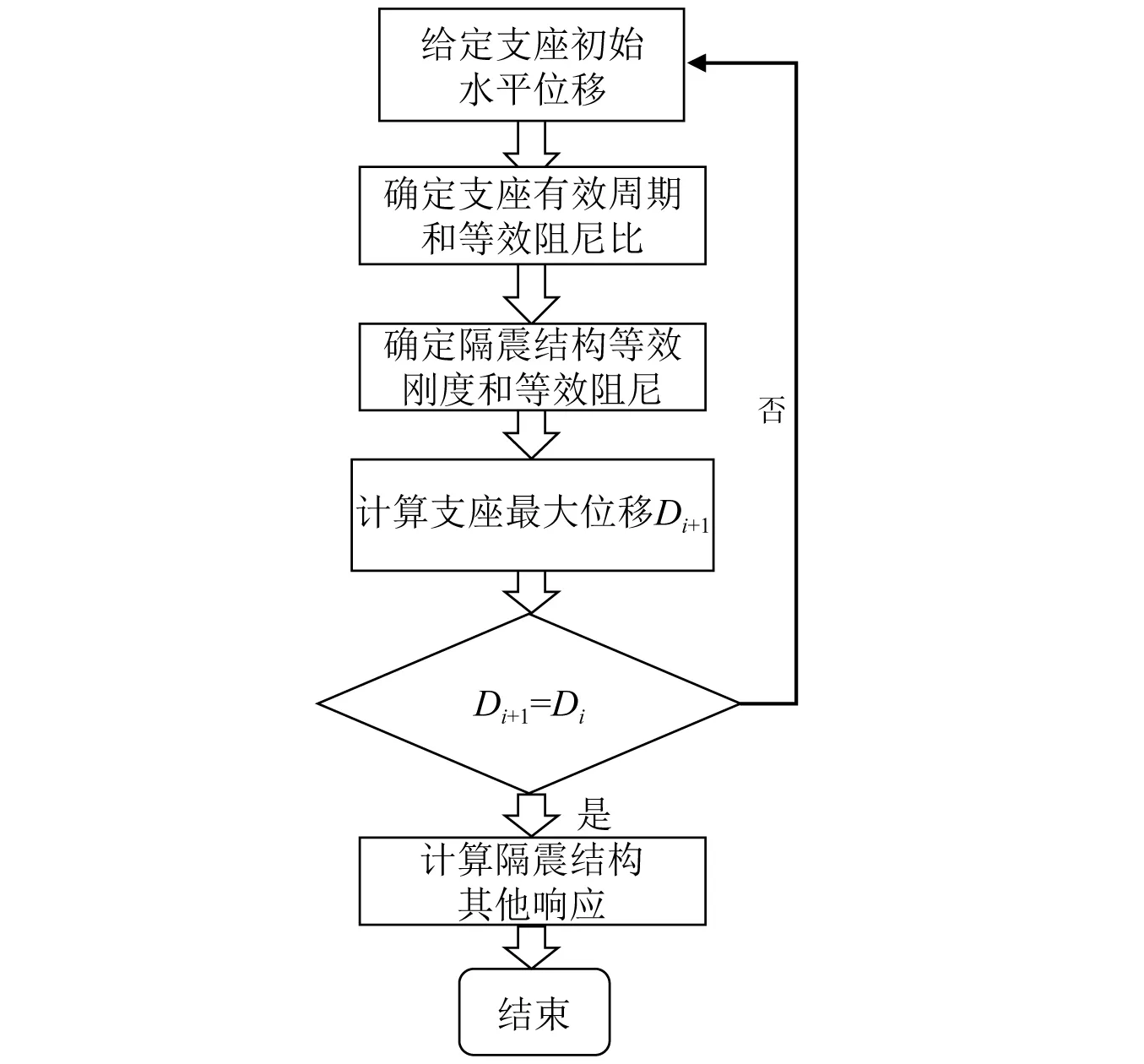
图2 支座等效刚度、阻尼比的迭代方法

3 阻尼矩阵构造影响分析

针对第1章隔震结构模型，为方便生成非比例阻尼矩阵，将隔震层和上部结构看作两个子结构。

3.1 分区瑞利阻尼方法

隔震层

cb=αbmb+βbkb

(13)

上部结构

Cs=αsMs+βsKs

(14)

式中：Ms、Ks分别为上部子结构质量和刚度矩阵；αb、βb、αs、βs分别为隔震系统子结构的瑞利阻尼比系数和上部子结构的瑞利阻尼比系数，由下式确定

(15)

(16)

ωi与ωj为对结构动力响应有显著影响的最高和最低频率。ξs、ξb分别为上部结构和隔震层的阻尼比。

此时隔震结构的整体非比例阻尼矩阵为

(17)

式中，cr为分区Rayleigh阻尼[20]，可得

cr=βs(-k1,0,…,0)

(18)

3.2 阻尼系数方法

图1隔震结构为剪切型模型，上部结构阻尼可以取与刚度成比例，通过各层的阻尼比、刚度，求得各楼层的阻尼系数

(19)

然后按照刚度矩阵组集的方式来组装整体的阻尼矩阵。求得整体阻尼如下式

3.3 瑞利-阻尼系数方法

对于隔震层上部结构可以采用瑞利阻尼形成阻尼矩阵，而对于隔震层或隔震支座则通过式(19)阻尼比换算成阻尼系数，然后按照刚度矩阵组集的方式来组装整体的阻尼矩阵。

对隔震层，通过支座的等效阻尼比、等效刚度，求得阻尼系数

(20)

对于上部结构可按瑞利阻尼假定形成阻尼矩阵，即

Cs=αsMs+βsKs

(21)

式中：Ms、Ks分别为上部子结构质量和刚度矩阵；αi、βi分别为相应的质量和刚度比例系数，由下式确定

(22)

式中：ωm与ωn为整体结构中对应于上部结构第m、第n阶自振频率；ξm、ξn为相应振型阻尼比。

然后按照直接集装两个子结构方式来组装整体的非比例阻尼矩阵。如式(23)所示。

(23)

3.4 振型叠加-阻尼系数方法

对隔震层，通过支座的等效阻尼比、等效刚度，求得阻尼系数

(24)

由于结构的各阶振型的阻尼比呈现非线性分布，因此对上部结构可采用Clough提出另外一种阻尼模型

(25)

式中：Ms为上部结构质量矩阵；ωi、φi、Mi分别为自振频率、无阻尼振型和振型质量。同样按照直接集装两个子结构方式来组装整体的非比利阻尼矩阵。

以10层剪切模型为研究对象，取刚度质量比k/m=1 767 s-2，所有振型的阻尼比为0.05。通过在结构底部更换不同参数的隔震层进行讨论分析。

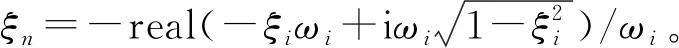
隔震层等效周期取为3 s。众所周知，隔震结构第一阶振型阻尼比主要由隔震层阻尼控制，高阶振型阻尼比主要由上部结构阻尼控制。由图3可知，当隔震层阻尼比大于0.05时，分区瑞利阻尼方法对隔震结构第一阶振型阻尼比的反映不够合理，远小于隔震层等效阻尼比；瑞利-阻尼系数方法给出的第一阶振型阻尼比稍大于隔震层等效阻尼比，但随着隔震层阻尼比的增大，两者越来越接近，特别需要指出的是，对于其他阶振型阻尼比，这方法给出的数值明显偏大，随着振型阶数的增大，阻尼比增大的程度也不断加剧；振型叠加-阻尼系数方法和阻尼系数方法相对比较合理，两者也非常接近，区别主要在于高阶振型阻尼比，后者较大。

图3 不同阻尼矩阵形成方式随隔震层等效阻尼比变化对振型阻尼比的影响

不同阻尼矩阵形成方式随隔震层等效周期Tb的变化对隔震结构振型阻尼比ξn的影响，如图4所示。图4中标注了前4阶振型阻尼比变化曲线，其他曲线为第五～第十阶振型阻尼比变化曲线。随着隔震层等效周期Tb的增大，第一阶振型阻尼比将趋近隔震层等效阻尼比。同时，其他阶振型阻尼比也将越来越靠近上部结构阻尼比。对于这两点规律，分区瑞利阻尼方法和瑞利-阻尼系数方法都没有很好地表达出来(见图4)。相对而言，振型叠加-阻尼系数方法和阻尼系数方法计算出的振型阻尼比随隔震层等效周期的变化趋势更为合理。

图4 不同阻尼矩阵形成方式随隔震层等效周期变化对振型阻尼比的影响

综上所述，阻尼系数法和振型叠加-阻尼系数方法构造的隔震结构阻尼矩阵，无论是隔震层的阻尼变化，还是刚度变化，都能够反应出隔震结构特性规律。然而分区瑞利阻尼的会对隔震一阶振型进行抑制，对高阶振型由会产生过阻尼现象，因此建议隔震结构采用振型叠加-阻尼系数和阻尼系数方法进行结构阻尼矩阵的构造。

4 结构算例分析

以一典型的10层框架剪切模型为研究对象，层质量m与层刚度k均匀分布，取刚度质量比k/m=1 767 s-2使得结构基本周期为1 s，所有振型的阻尼比为0.05。在结构底层增加隔震层，如图5所示。

图5 隔震结构分析模型

4.1 基于近、远地震波反应谱分析

为了得到阻尼矩阵形成方式对反应谱CQC与反应谱CCQC两种方式计算方式的影响，避免由于反应谱计算(速度反应谱估计、阻尼修正系数)引起的影响，从而采用天然波的反应谱比较系统的研究阻尼矩阵形成方法、隔震层等效阻尼比、等效刚度、地震动特性对两种方法精度的影响。在这方式中，地震动记录选取ATC-63推荐的28组近场地震和22组远场地震，其中把每组地震动加速度峰值最大的分量调至0.4g。

两组地震作用下采用不同阻尼矩阵形成方法上部结构底部剪力随隔震层等效阻尼比的变化曲线，如图6、图7所示。每幅图中，隔震层等效周期为3 s，“TimeHistory”表示基于时程分析的所有地震动作用下最大基底剪力的平均值Vb，“CQC”表示对每一条地震动反应谱进行强迫解耦的CQC组合后取平均，“CCQC”表示对每一条地震动反应谱进行强迫解耦的CCQC组合后取平均。此外，所有的基底剪力通过阻尼系数方法求得的隔震层等效阻尼比为0时的基底剪力进行标准化。

由图6、图7可知，在隔震层阻尼比小于0.05时，“TimeHistory”、“CQC”和“CCQC”计算出的基底剪力重合时，说明隔震层阻尼的非比例影响可以忽略，这时可以采用任意一种阻尼矩阵构造方法。当隔震结构阻尼大于0.05时，4种阻尼构造方式结构分区瑞利阻尼方法得到结果与其他3种方法差别最大，没有反映出非比例阻尼的影响。除数值大小有差别外，瑞利-阻尼系数方法、振型叠加-阻尼系数方法、阻尼系数方法得到的基底剪力随隔震层阻尼的变化趋势基本一致。隔震结构基底剪力与构件内力大小息息相关，隔震结构阻尼比一般在0.1～0.3，在此范围内阻尼系数方法反映出的结构基底较大。由此可知，进行隔震结构设计时，并且结构阻尼比大于0.05时，优先选用阻尼系数方法较为合理。

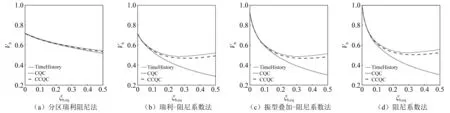
图6 近场地震作用下阻尼矩阵形成方式对结构响应的影响

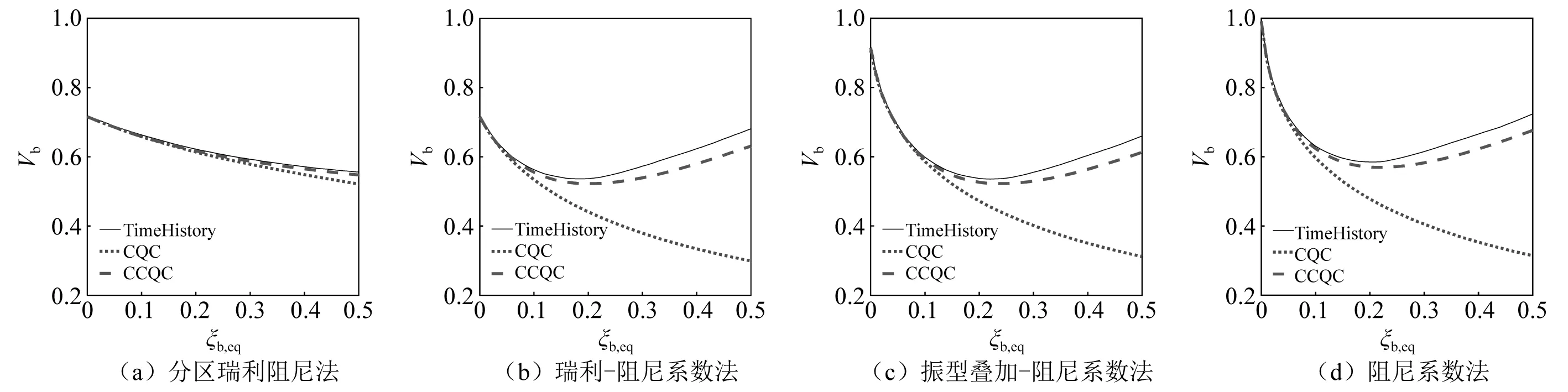
图7 远场地震作用下阻尼矩阵形成方式对结构响应的影响

通过上述研究发现阻尼系数方法更适合用于隔震结构的阻尼矩阵构造，在此基础上为探究两种方法的计算精度，在后面的计算中统一采用阻尼系数方法来形成阻尼矩阵。取隔震层等效周期为3 s，下标“rsm”表示反应谱方法CQC或CCQC，“thm”表示时程分析方法。对于每一条地震动按照CQC、CCQC和时程分析方法分别计算结构响应，然后以时程分析结果为基准得到CQC和CCQC的相对误差，最后将所有地震动作用下的计算误差进行平均示于图中。图8～图11中，同一种方法的计算结果用同一种线型表示，每一种方法包含若干条曲线，对应各个楼层的地震响应计算误差。

图8 近场地震作用下CQC与CCQC对比

两组地震作用下，CQC与CCQC的计算精度随隔震层等效阻尼比的变化如图8、图9所示。可以发现，对于上部楼层位移，当结构隔震层阻尼比ξb,eq在0.05以内时，两种方法精度相当，可以选择任意一种。然而隔震结构阻尼比一般在0.1～0.3，从图8、图9中可以发现在此区间范围，CQC预测结果稍偏小；对于层间剪力，CQC预测结果偏小较多，此时不能选择CQC方法。若将计算精度控制在±10%以内的话，CQC的适用范围依然在0.05以内，即非隔震结构。此外，可以发现近场地震作用下的CQC计算误差显著大于远场地震作用。这是因为近场地震相对远场地震强度更大，并且具有脉冲效应，进一步说明CQC方法对远场、近场地震作用比较敏感，采用此方法前，应对地震波的选取更加谨慎。而CCQC方法无论在远场还是近场地震下，误差波动小且预测精度较好。

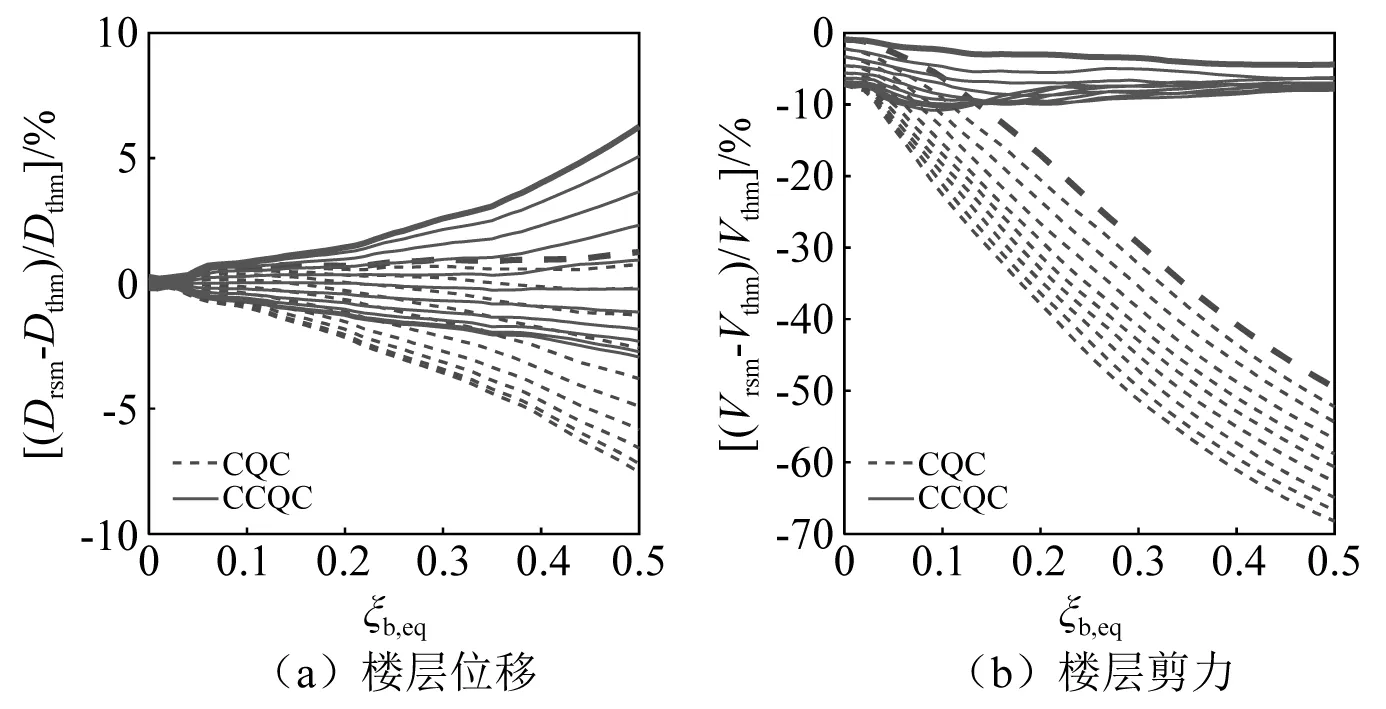
图9 远场地震作用下CQC与CCQC对比

取隔震层等效阻尼比为20%，两组地震作用下，CQC与CCQC的计算精度随隔震层等效周期的变化如图10、图11所示。可以发现，对于楼层位移，随着隔震层有效周期的增大，CQC与CCQC的计算精度得以提高，CCQC预测值始终比CQC稍大；对于楼层剪力，随着隔震层有效周期的增大，CQC的计算误差也越来越大，近场地震作用下更为显著。结合上述，可以发现CQC反应谱方法会严重低估隔震结构的楼层剪力，从而会对结构设计产生重大影响，而近场地震作用下，CQC方法预测误差会加大，因此建议在对结构进行隔震设计时，考虑采用CCQC方法。在使用CQC方法时不仅需要考虑结构的阻尼比范围，还需要同时进行近、远场地震作用分析，以便确定安全设计方案。

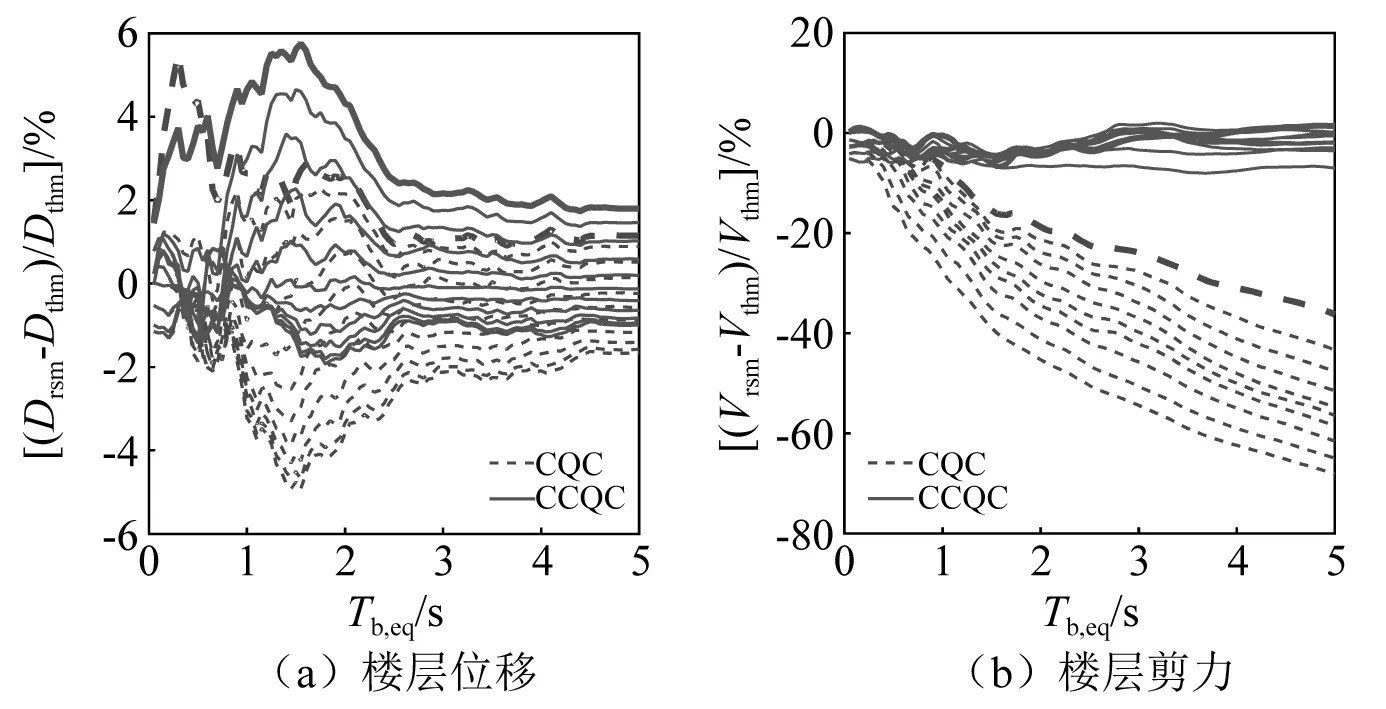
图10 近场地震作用下CQC与CCQC对比

图11 远场地震作用下CQC与CCQC对比

4.2 设计反应谱分析

对于隔震结构第一阶振型阻尼比远大于5%，而高阶振型阻尼比又有可能小于5%。阻尼比为2%、5%、10%、20%、30%时规范设计反应谱与人工加速度平均反应谱的对比，如图12所示。图12中相同阻尼比的规范谱和设计反应谱采用相同的线型和颜色。由图12可知，随着阻尼比的增大，设计反应谱与人工加速度平均反应谱的差别越来越大，而且人工加速度平均反应谱值在整个周期段普遍偏小。可以预测隔震层阻尼比越大，基于设计反应谱的反应谱方法计算结果将越大于时程分析结果。这是由人工加速度时程不能兼容多阻尼比目标谱导致的，因此本文人工波生成采用隔震层阻尼比修正的设计反应谱为目标谱。

图12 不同阻尼比规范设计反应谱与人工加速度平均反应谱

在工程实践中，不论是CQC方法还是CCQC方法都需要基于设计反应谱进行峰值响应组合，因此分析此种情况下的CQC与CCQC方法的特性更具有实用意义。为与时程分析结果对比，以设计反应谱为目标谱，采用时域内余弦调幅的方法生成30条人工加速度时程的反应谱以及与设计反应谱对比，如图13所示。

图13 30条人工波反应谱及其平均值与规范设计反应谱间的对比

采用3种方法进行动力响应分析，即反应谱方法CQC、CCQC和时程分析方法。CQC(code spectra)、CCQC(code spectra)分别表示在基于强迫解耦的CQC组合和CCQC组合中采用设计反应谱；需要指出的是，CCQC(code spectra)中，速度反应谱由(伪加速度)设计反应谱转换成的伪速度反应谱近似，对于阻尼比的谱值由抗震规范提供的阻尼修正系数来调整。CCQC(synthetic acc spectra) 表示CCQC组合中采用由30条人工加速度时程计算出的平均位移反应谱和速度反应谱。上述3种反应谱方法求得的结构响应以下标“rsm”表示，下标“thm”表示时程分析得出的平均结构响应。所有计算出的结果，以时程分析结果为基准，进行对比，分析不同计算方法的精度。图14、图15中，同一种方法的计算结果用同一种线型表示，每一种方法包含若干条曲线，对应各个楼层的地震响应。

图14 隔震层等效阻尼比对CQC与CCQC计算精度的影响

图15 隔震层等效周期对CQC与CCQC计算精度的影响

首先，假定隔震层等效周期Tb,eq=3 s，研究隔震层等效阻尼比ξb,eq对CQC与CCQC计算精度的影响，如图14所示。图14(a)为3种反应谱方法楼层位移误差，CCQC(synthetic acc spectra)精度最高，CQC(code spectra)与CCQC(code spectra)结果非常接近，但随着隔震层等效阻尼比的增大，计算结果越来越大。因此，在常用的隔震层等效阻尼比在0.1～0.3内，采用基于设计反应谱的CQC或CCQC方法预测的楼层位移(包括隔震层位移)稍偏于保守。而对于楼层剪力、楼层倾覆弯矩CQC(code spectra)与CCQC(code spectra)差别非常显著，同样在ξb,eq在0.1～0.3内，所有楼层CCQC(code spectra)的精度在-10%～10% (负号表示小于时程结果)，CQC(code spectra)在-1%～-40%内，而且其各个楼层计算误差较为分散，楼层位置越高误差越大。图中实线为CCQC(synthetic acc spectra)，是用真实的反应谱值进行组合，但楼层剪力和楼层倾覆弯矩比时程结果稍小，在10%以内。综合上述所言，当结构阻尼在0.05以内， CQC和CCQC反应谱方法预测结构响应都偏小，此时建议采用CCQC(synthetic acc spectra)，较为精准。当隔震结构等效阻尼比处于0.1～0.3时，采用CCQC反应谱方法最为保守，符合我国的设计思想。

假定隔震层等效阻尼比ξb,eq=20%，研究隔震层等效周期Tb,eq对CQC与CCQC计算精度的影响，如图15所示。当隔震层等效周期小于1 s时，对结构响应起主导作用的振型阻尼比均在5%以下，而此时人工加速度平均反应谱在周期0～1 s段大于设计反应谱值，从而导致在隔震层等效周期小于1 s的区域内，时程结果大于基于设计反应谱的CQC、CCQC计算结果。由于上部结构基本周期为1 s，通常隔震之后的基本周期远大于1 s。因此，本文主要关注隔震层等效周期大于1 s的情况。对楼层位移，基于设计反应谱的CQC与CCQC方法非常接近，同时随着隔震层等效周期的增大，计算结果也不断增大，如图15(a)所示。而对于楼层剪力和倾覆弯矩在2～4 s，基于设计反应谱的CQC与CCQC方法差别较大，从图15可知，基于设计反应谱的CCQC方法计算结果均大于时程分析结果，而基于设计反应谱的CQC方法计算结果明显偏小，特别是较高楼层位置，而且随着隔震层等效周期的增大，这种偏小的程度进一步加剧。此外，对于红色曲线表示的基于人工加速度平均反应谱的CCQC方法，其计算出的楼层剪力比时程结果稍小，但隔震层等效周期对其影响不大。因此当隔震结构周期处于2 s以上时，建议采用CCQC方法。