水平土层地震响应地面峰值加速度可靠度研究

梁师俊， 蒋 蓓

(浙江建设职业技术学院 建筑工程学院，杭州 311231)

结构抗震设计中最关键的问题是确定场地的地震动参数，其中，地面峰值加速度(ground peak acceleration，GPA)是场地地震动参数中一个重要的物理量，具有非常重要的作用。但是，一方面，地震是一种随机现象，具有非常强的随机性，地震发生的时间、地点和传播都具有强烈的不确定性，即使在同一次地震中，相隔几十米位置处测得的地震特征都不尽相同[1-2]；另一方面，场地条件对地震响应有很大的影响，其影响不仅表现在对频谱特性的影响上，还表现在地面峰值加速度上[3-6]，而场地条件中的土层特性、力学参数等都无法准确测量，也具有一定的不确定性。在场地条件和输入地震双重不确定影响下，地震引起的地面响应，特别是地震作用引起的场地地面峰值加速度具有强烈的随机性[7]，因此，以置信区间来表征地震响应场地地面峰值加速度的可靠性，以更好的反映土层地震反应分析的计算结果，为进行结构抗震可靠性分析提供更为准确的峰值加速度概率分布，对于结构的抗震设计和地震风险分析都具有十分重要的意义。

目前，针对地震响应可靠度分析主要集中在结构可靠度分析[8-10]、地震响应下边坡稳定性的可靠度分析[11-12]、地基抗震安全性的可靠度分析[13-14]等方面，分析方法包括基于随机有限元法的摄动法[15]、路径积分法[16]等，基于抽样数值模拟的蒙特卡洛模拟[17]、子集模拟等。针对地面峰值加速度分析主要集中在场地条件对地面峰值加速度离散性及空间变异性分析[18]、软土层对峰值加速度的影响等,如陈国兴等[19]采用集中质量模型非线性分析法进行钻孔土柱地震反应分析，提出了场地卓越周期的弱震预测法，给出了场地卓越周期和地面峰值加速度的空间变化特征，刘方成等[20]分析了场地内软土层的几何特征(厚度与埋深)和剪切波速变化对地面峰值加速度的影响。在土层地震响应分析研究方面，主要集中在动剪切模量比、密度和剪切波速等土层参数对地表地震动的影响上[21]。

综上所述，尚缺少一种同时考虑地震随机性及场地条件随机性双种不确定影响下地面峰值加速度可靠性分析研究方法。本文根据收集的浙江某地科技城100例土动力学试验资料，基于Flac 3D软件以等效线性分析方法计算了场地地面峰值加速度，继而拟合了地面峰值加速度的概率密度函数。并从等效场地剪切波速的概率分布出发，推导了地震响应地面峰值加速度的概率密度函数，开展了地面峰值加速度的置信区间分析。

1 试验数据

某科技城覆盖区域近30 km2, 场地新布置地震钻孔29个、勘察钻孔30个、已有钻孔41个，共计各类钻孔100个。场地地处长江三角洲冲海积平原地区，地层成因复杂，区内第四系为一套河流冲积及河湖相、滨海相松散沉积物，根据勘探孔资料，土层自上而下分别为：填土、粉质黏土、淤泥质粉质黏土、粉质黏土、粉质黏土夹粉土、砂质粉土夹粉质黏土、粉砂、粉质黏土、粉质黏土夹砂质粉土，场地地质如图1所示。

图1 地质剖面图

区域场地共取得常规土样248组、动三轴试样83组，通过室内试验、现场波速测试、动三轴试验测定土层天然含水量、密度、空隙比、饱和度、液限、塑限、液性指数、塑性指数、压缩系数，压缩模量、抗剪强度、剪切波速、动剪切模量比、动阻尼比等参数。

根据以上土层参数，综合土层分层、剪切波速、重度、动剪切模量比和动阻尼比与动应变关系等土层模型参数，确定场地100个钻孔土层模型。

2 等效场地剪切波速的概率分布

在水平成层场地中，设场地第i层土的厚度为hi,动剪切模量为Gi,剪切波速为vi,密度为ρi。

定义等效场地剪切波速vs，按下式确定

(1)

定义场地等效密度ρ，按土层厚度加权平均密度确定，即

(2)

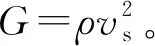
由于剪切波速为一随机测试值，不可避免的存在误差，且其误差符合正态分布，对于等效场地剪切波速vs，其误差也应符合正态分布，先分别假定符合正态分布、对数正态分布两种分布情况，再采用J-B检验和K-S检验对收集的某场地100例土样试验结果，进行假设检验。

2.1 等效场地剪切波速的概率分布拟合

用正态分布和对数正态分布对收集样本场地等效剪切波速vs进行拟合。

收集样本等效场地剪切波速vs的概率密度拟合情况及累计概率密度拟合情况，如图2所示。

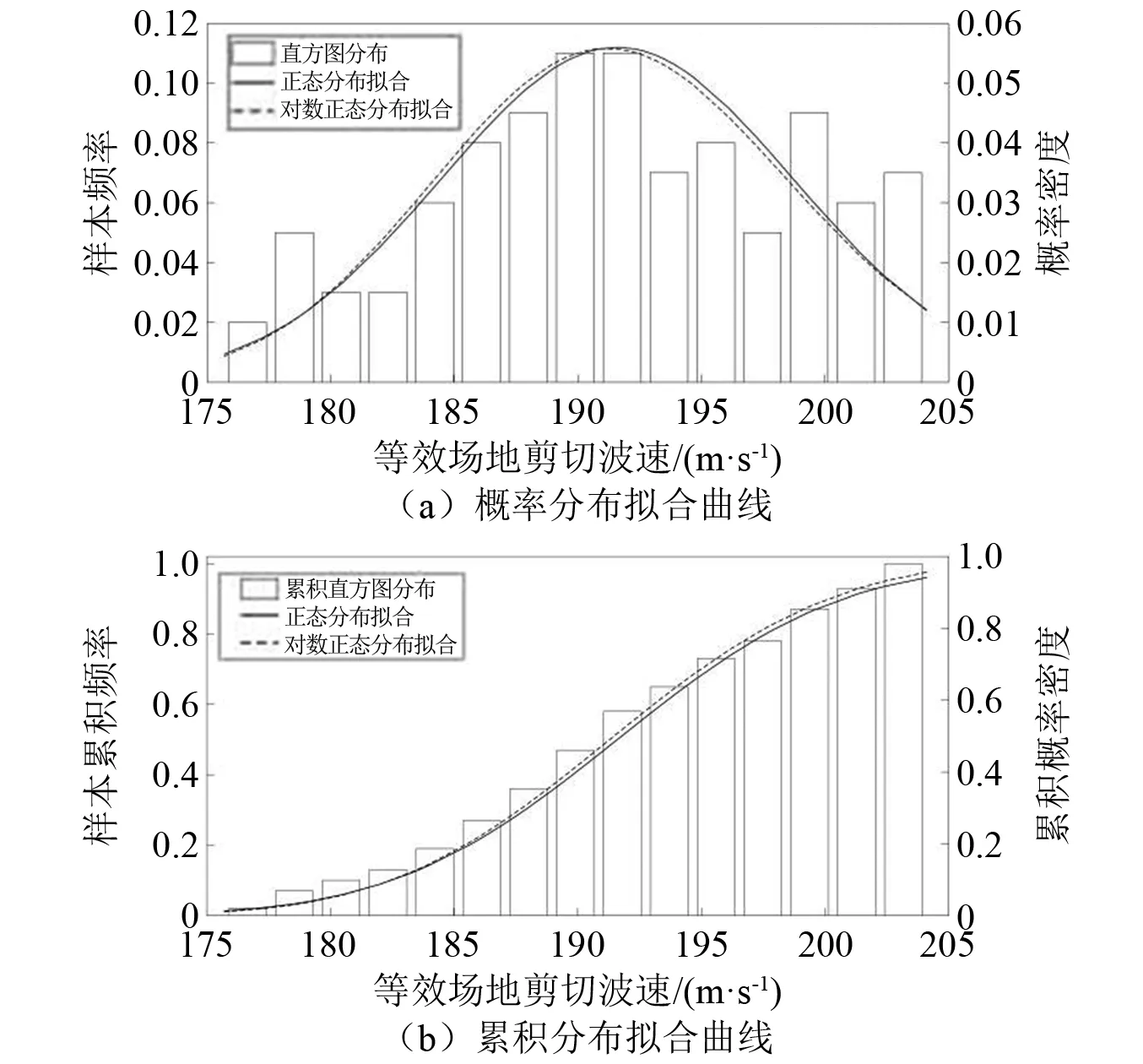
图2 场地等效剪切波速的概率分布拟合

从图2可知，不管是正态分布还是对数正态分布都与样本直方图经验概率密度分布接近，可以假定等效场地剪切波速同时符合正态分布与对数正态分布。拟合参数期望和标准差如表1所示。

表1 两种概率分布拟合参数

2.2 等效场地剪切波速的概率分布假设检验

对于收集的100个动剪切模量样本，在显著性水平为5%和10%下进行J-B检验、K-S检验，检验结果如表2所示。

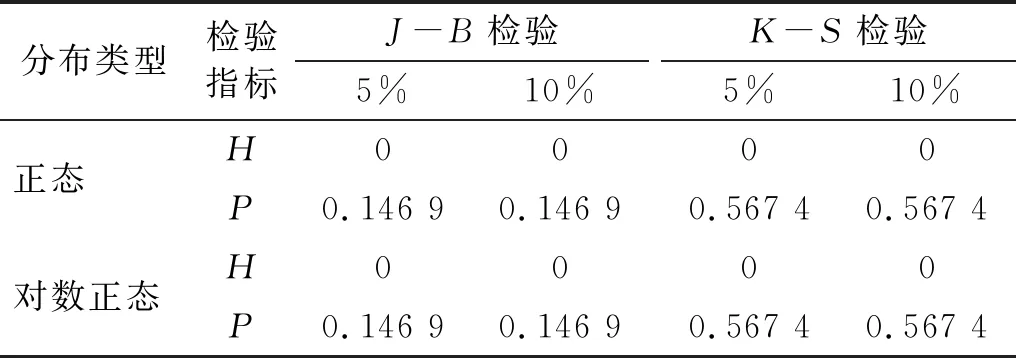
表2 等效场地剪切波速的假设检验结果

从表2可知，J-B检验、K-S检验的检验结果均是H=0，表明不能拒绝原假设，即正态分布、对数正态分布在5%和10%显著性水平下都通过了J-B检验和K-S检验。另外，接受假设的概率值分别为0.146 9、0.567 4，也均大于显著性水平，也表明可以接受假设检验。

假设检验结果与图1分布图形都表明，等效场地剪切波速既服从正态分布又服从对数正态分布，为计算简便，本文以正态分布来描述等效场地剪切波速概率模型，即

vs～N(uvs,σvs)

(3)

3 地面峰值加速度概率分布

(4)

(5)

βi为与第i振型的自振周期Ti相应的加速度动力放大系数，根据GB 5011—2010《建筑抗震设计规范》[23]按下式确定

(6)

一般地，参数η=0.45，γ=0.9～1.0，βmax=2.25。

自振周期Ti按下式计算

(7)

ϖi为第i振型的频率，可按下式确定

(8)

式中：H为场地地震反应计算深度；G为等效场地剪切模量；ρ为等效场地密度；vs为等效场地剪切波速。

将式(8)代入式(7)，场地自振周期可化为

(9)

将式(5)～式(9)代入式(4)，可以得到

(10)

令

(11)

(12)

特别地，当γ=1.0时，α表示为

(13)

(14)

E(max)=α(1)·E(vs)

(15)

(16)

4 地面峰值加速度分布的数值分析

4.1 模型及计算结果

根据收集的100例钻孔土层数据，建立Flac 3D软件三维分析模型，模型水平方向网格长度设为1 m，纵向网格长度综合考虑地质分层和剪切波速分层结果设为0.5 m。模型水平方向均设置自由场边界条件，纵向底面设置安静边界条件，各土层均施加滞后阻尼,Flac 3D软件三维分析模型如图3所示。

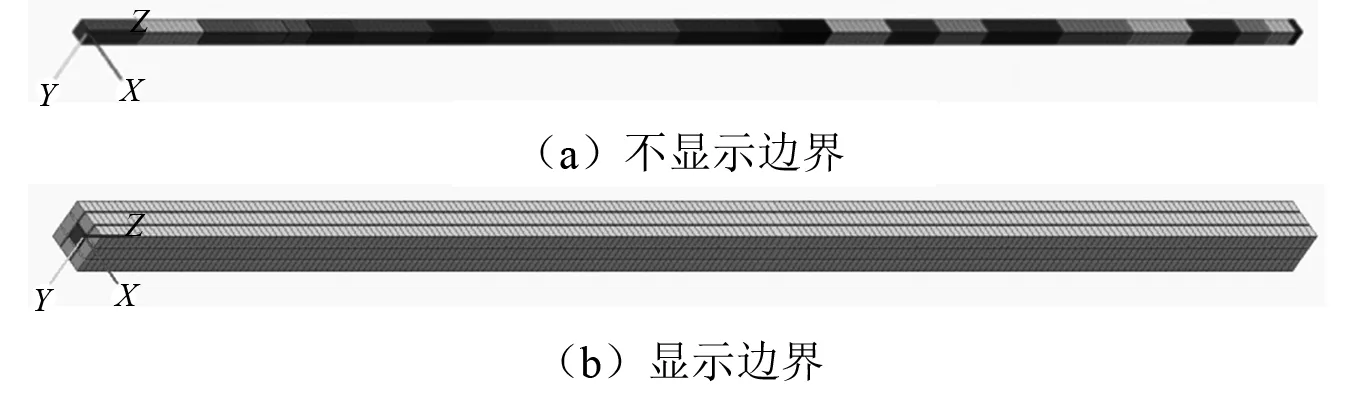
图3 Flac 3D软件模型

场地土层地震反应模型所需的土层密度、深度和厚度、剪切波速等，均采用现场勘察和实际测试数据。

以钻孔风化深度作为土层地震反应分析的基岩输入面，分别按50年超越概率2%、10%、63%输入人工拟合加速度时程，如图4所示。

图4 输入加速度时程

50年超越概率2%、10%、63%输入加速度峰值分别为151 gal、72 gal、18 gal。

计算得到不同超越概率水准下地面加速度时程各100条，50年超越概率2%时地面峰值加速度绝对值最大值为152 gal，最小值为125 gal，平均值为137 gal；50年超越概率10%时地面峰值加速度绝对值最大值为72 gal，最小值为55 gal，平均值为63 gal；50年超越概率63%时地面峰值加速度绝对值最大值为18 gal，最小值为14 gal，平均值为16 gal，如表3所示。

表3 地面峰值加速度

4.2 概率分布拟合

表4 地面峰值加速度拟合参数

图5 50年超越概率2%的地面峰值加速度概率分布拟合

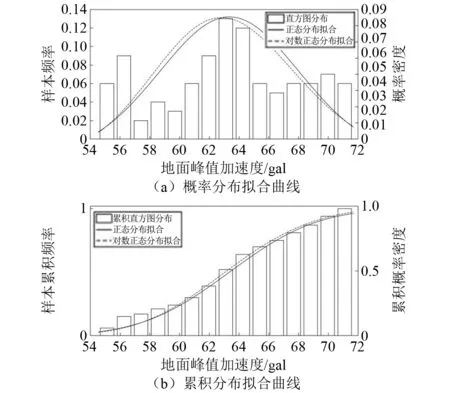
图6 50年超越概率10%的地面峰值加速度概率分布拟合

图7 50年超越概率63%的地面峰值加速度概率分布拟合

4.3 假设检验

表5 地面峰值加速度的假设检验结果

从概率密度分布拟合分布图形与假设检验结果看，可以认为，3种超越概率水准下地面峰值加速度均服从正态分布，即

(17)

式中：ξ为超越水准；uξ、σξ分别为对应超越水准的期望值和标准差。

5 地面峰值加速度的可靠度分析

由地面峰值加速度概率分布及地面峰值加速度分布的数值分析均可知，各超越水准下地震响应的场地地面峰值加速度符合正态分布，作标准化处理，进一步可以得到

(18)

则当显著性水平α，即可靠度为1-α下，随机变量y的置信区间为

(19)

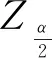
将式(19)代入式(18)，即得

(20)

(21)

(22)

则式(21)改写为

[uξ-Δξ,uξ+Δξ]

(23)

100例实测数据3种超越概率水准的地面峰值加速度在1%、5%、10%显著性水平下，由等效场地剪切波速概率分布(采用γ=1.0的近似值)和直接拟合地面峰值加速度概率密度函数分析得到的最大允许偏差及置信区间情况，如表6、表7所示。

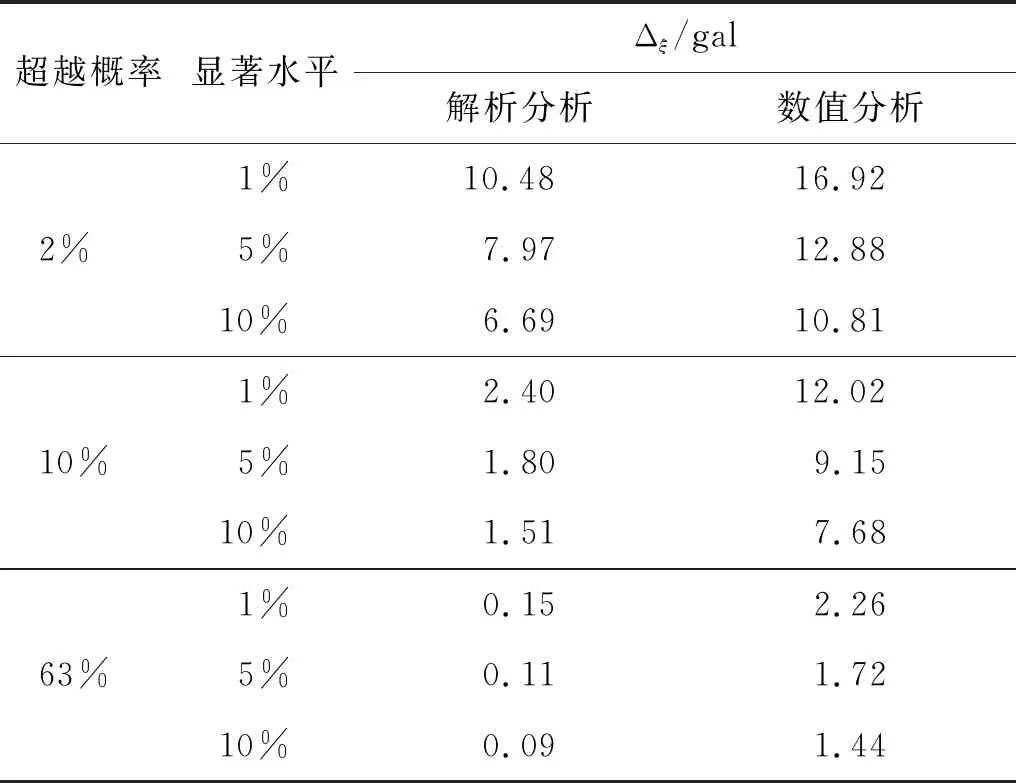
表6 1%、5%、10%显著性水平下的Δξ

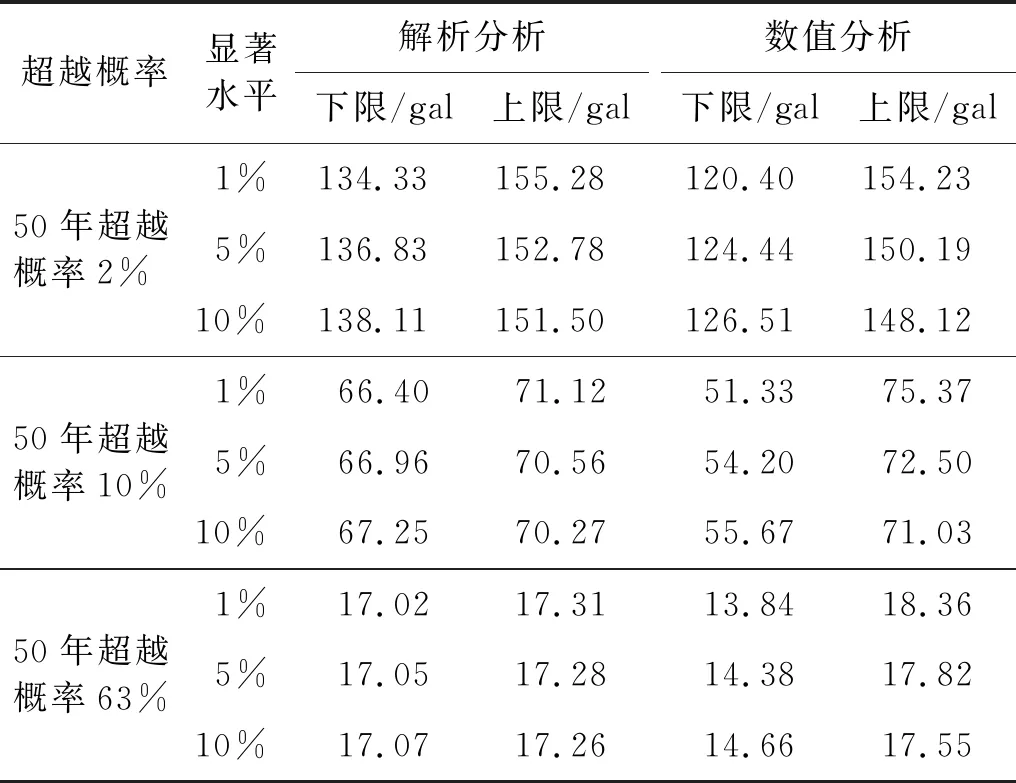
表7 1%、5%、10%显著性水平下的置信区间

从表6、表7可知：由等效场地剪切波速概率分布经解析分析得到的最大允许偏差值都较由数值分析直接拟合地面峰值加速度概率密度函数分布分析得到的最大允许偏差少，也即解析分析上下限值间距较数值分析小；且不管是解析分析还是数值分析，同一超越概率水准下，显著性水平越小最大允许偏差越大；同一显著性水平下，超越概率越大，最大允许偏差越少。

50年超越概率2%、10%、63%经解析分析及数值分析计算的场地地面峰值加速度分布情况及与各置信水平最大偏差值对比情况，如图8～图10所示。

图8 50年超越概率2%下地面峰值加速度分布

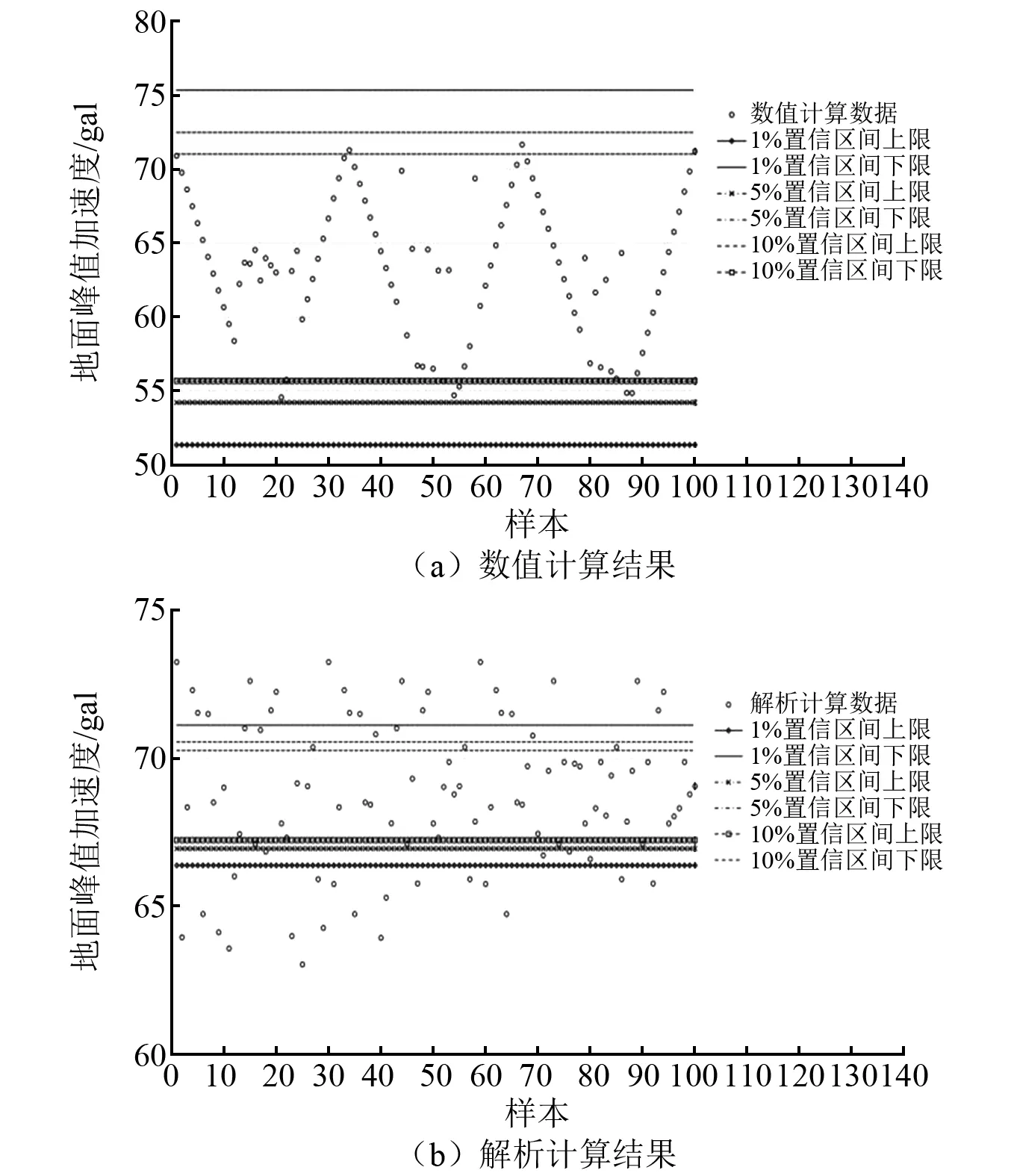
图9 50年超越概率10%下地面峰值加速度分布

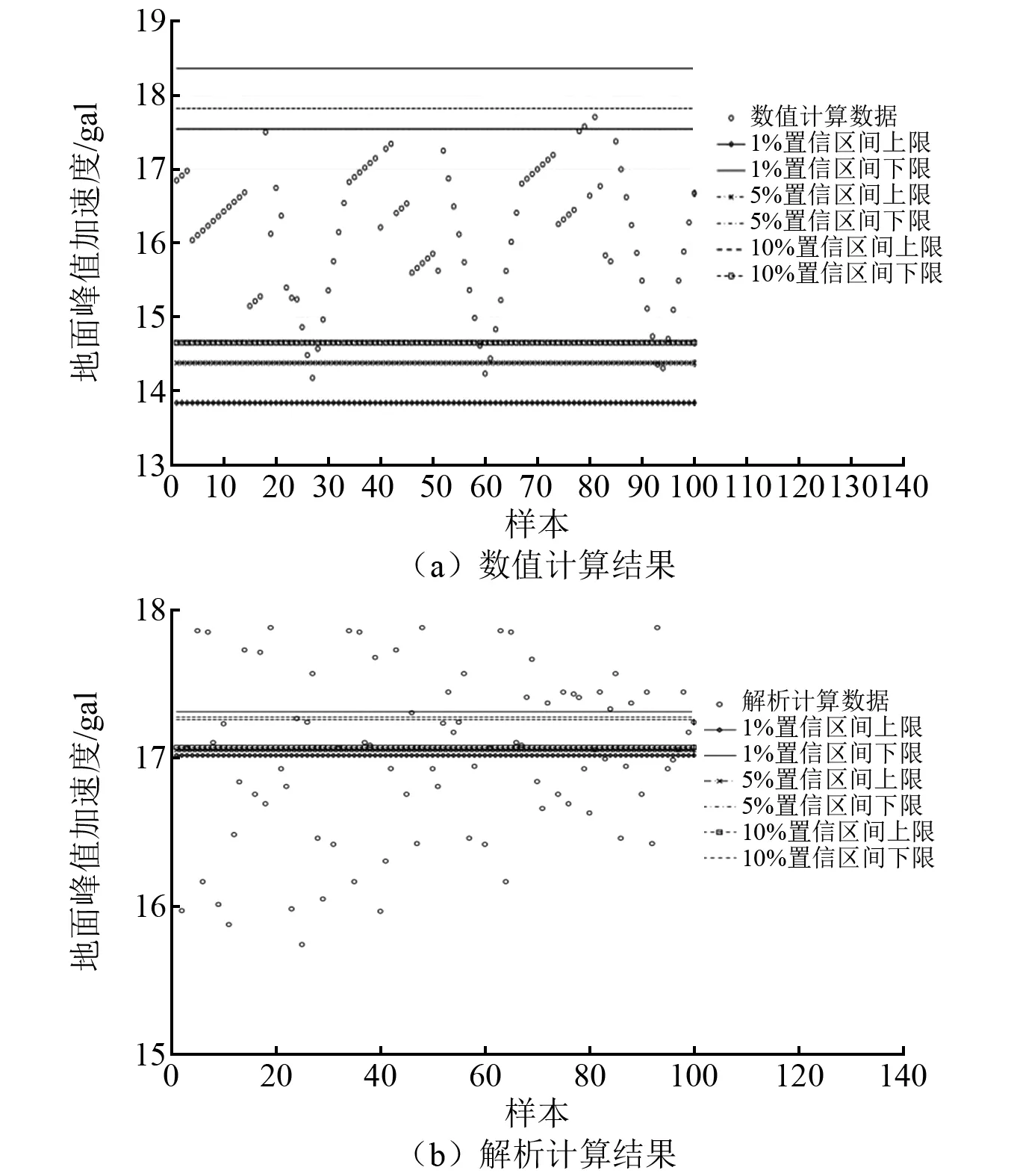
图10 50年超越概率63%下地面峰值加速度分布

实际上，从表6、表7也可知，50年超越概率10%和63%下地面峰值加速度也表现出同样的规律。

比较两种情况，可以发现，由解析分析得到的地面峰值加速度较由等效场地剪切波速经数值分析直接仿真得到的地面峰值加速度分布更离散。

从上述分析可知，水平土层地震响应地面峰值加速度不同分析方法具有不同的可靠性分布。建议在进行结构抗震、地基抗震可靠度、地基抗震安全性可靠度等分析时，应充分考虑地面峰值加速度置信区间的影响。

6 结 论

根据某科技城地100个钻孔土层模型，从等效场地剪切波速概率分布出发，推导了地震反应时地面峰值加速度的概率密分布函数，并基于Flac 3D软件开展了场地地震反应分析，拟合了地面峰值加速度的概率密分布函数，主要结果如下：

(1) 不管是基于场地土动剪切模量概率分布解析推导，还是基于场地地震响应有限元分析结果拟合，地面峰值加速度均服从正态分布。

(2) 给出了地面峰值加速度置信区间的方程。由等效场地剪切波速概率分布经解析分析得到的最大允许偏差值都较由数值分析直接拟合地面峰值加速度概率密度函数分布分析得到的最大允许偏差少。由数值分析直接仿真得到的地面峰值加速度较由等效场地剪切波速经解析分析得到的地面峰值加速度分布更离散。