品味转化思想，拨开思维迷雾

徐清

【摘 要】学生数学思想方法的培养，不可能“一蹴而就、立竿见影”，而是一个“水滴石穿”的过程。转化思想是数学学习中一种重要的思想方法。学生面对一个陌生的或复杂的问题时，常常感到迷茫而束手无策，此时教师若运用将未知转化为已知、复杂转化为简单、一般转化为特殊、抽象转化为具体等转化思想来启迪，则学生会拨开思维的迷雾，让答案水落石出。

【关键词】数学教学 转化思想 数学思维

在教学中，经常会遇到这样的学生，独立简单的知识点他掌握了，可是变一下情境或者稍微复杂一点就不会了;有时候听教师或同学讲时好像会了，可自己一做题却又不会了。这到底是什么原因引起的呢？是学生只会简单地模仿，没有内化成自己的知识，还是理解不到位，缺乏举一反三的能力呢？笔者认为，其核心原因还是没有形成最基本的数学思想方法。

数学思想方法蕴含在小学数学学习的各个阶段，随着数学知识的不断习得而悄悄滋润着学生的大脑，潜移默化地促进学生的认知过程。在解决数学问题时，最基本的思想就是转化思想。转化思想是一种化归思想，一般是将复杂的问题转化为简单的问题，将抽象的问题转化为具体的问题，将未解决的问题转化为已解决的问题，进而衍生出新的方法。

一、教学过程中引发的思考

在教学空间与图形总复习时，有些学生经常会被“求阴影部分图形的面积”这种类型的题目难到。如图1，分别以三角形的三个顶点为圆心，作半径为2分米的圆，求阴影部分的面积。

部分学生会这样思考：把三个扇形的面积分别求出来，然后加起来，但是发现三角形的三个内角角度不知道，无法求出三个扇形的大小，于是苦思冥想找不出解决问题的突破口;而部分学生却觉得很简单，根本不需要求出每个扇形的面积，因为每个圆的大小是一样的，也就是半径是相同的，所以这三个扇形可以拼在一起，又因为三角形内角和是180°，所以三个扇形拼在一起后是一个半圆，只需要求出半径是2分米的半圆面积就可以了。

不同学生对这道题的思考方式不同，很明显可以发现，后一部分学生能解决这道题目的关键在于他们运用了转化的方法，他们的数学思维中有转化的思想，这正是前一部分学生所缺少的思想方法。

二、转化思想在小学数学教学中的重要意义

《义务教育数学课程标准（2011年版）》提出：将基础知识、基本技能、基本思想和基本活动经验作为数学课程的总目标。小学常用的基本思想有转化思想、数形结合思想、集合思想、模型思想、统计思想等，其中转化思想既是其他数学思想的基础，又是各种数学思想的灵魂，贯穿于小学数学教学内容的始终。但是因为转化思想分布在各个年级不同的教学内容里，所以教师在教学时有时会忽略，有时为了赶进度，重视了数学方法，而忽略了数学思想，导致有些学生对于教师讲过的经常见到的题目能很快解答，而对于一些新颖的题目就无从下手。这就需要教师在教学时有意识地培养学生的转化思想，让学生能真正理解并有效运用。

三、转化思想在小学数学教学中的应用

（一）转化是探究新知的基本策略

小学数学很多知识都是以旧知识为基础的，在旧知识的基础上不断发展、变化和提升，进而形成新知识。而将未知的转化为已知的，简单地说就是将“新知”转化为“旧知”，利用“旧知”解决“新知”，这样更有利于学生的记忆，因为它能帮助学生了解知识的形成过程。

1.讓“算理”融入“算法”

在探索运算法则时，教师常常会重“算法”而轻“算理”，学生知其然而不知其所以然。而培养学生转化的思想，可以促进学生对算法的理解。

例如，在学习“小数乘整数”时，出现例题，“一个风筝3.5元，买3个风筝需要多少钱？”当学生列出算式“3.5×3”时，可以让学生主动探索如何计算出结果。部分学生想到乘法的意义，把“3.5×3”表示成“3.5+3.5+3.5”，运用小数加法计算来解决;也有部分学生想到把3.5元换算成35角，转化成整数乘法来计算，最后再将单位换算成“元”，同时通过这种方法还能引出小数乘法的计算方法，让学生进一步从意义上来理解，而不是只知算法，不知算理。无论哪种方法，学生都是把新知识转化成已学过的知识，逐步感知到了转化的思想方法。

2.让“背公式”变成“促思维”

在探索图形计算公式时，如果只是简单地让学生记忆公式，而忽略了这个公式是如何来的，那么当这个公式一段时间不用时，学生常常会遗忘。这就需要教师在设计教学时，让学生主动探索公式的推导过程，从而培养学生转化的思想，促进学生思维的发展。

例如，在教学“圆的面积”时，如果简单地让学生记忆“圆的面积=πr2”，学生的数学学习只停留在了记忆的层面，思维得不到发展。教师应引导学生根据平行四边形、三角形、梯形面积推导的经验，把圆的面积转化成已经学过的图形面积进行推导。虽然圆是由曲线围成的图形，和前面直线围成的图形有一定的区别，但是通过剪拼我们还是能把它转化成近似的已经学过的图形，通过分成8份、16份后拼一拼，让学生慢慢感知“越来越接近平行四边形”的感觉，同时渗透“化曲为直”和“数学的极限思想”，就能理解圆的面积求法了。这个教学例子也充分体现了转化思想是其他数学思想的基础。

（二）转化是解决问题的重要方法

1.化繁为简，活转化

著名的数学家波利亚说过：“当原问题看来不可解时，你不要忘记人类的高明之处，就在于迂回绕过不能直接克服的障碍，就在于能想出某些适当的辅助问题。”复杂运算往往都是由几个简单的运算叠加而成的，利用转化方法就可以实现复杂运算的分解。学生如果掌握了转化思想，就能提高自身思维的敏捷性和灵活性，为今后的学习生活打下坚实的基础。

在简便运算的教学中，有些人觉得计算就是一种技能，没有什么数学思想可言，其实不然，简便运算既能让学生掌握计算的技能、技巧，又能训练学生的转化思想，使学生的计算能力有质的飞越。例如，在计算“25×36”时，如果不思考就动笔，第一反应就是列竖式计算，而且每个学生都有这样的基础，但是爱思考的学生会找到解题窍门，避免纷繁复杂的笔算。通过一题多解的方法，灵活运用简便运算的方法进行转化，只要把算式进行如下转化，就能口算出计算的结果。

2.化数为形，巧转化

借助于图形的性质将许多抽象的数学概念和数量关系形象化、简单化，可以给人以“直观感”。

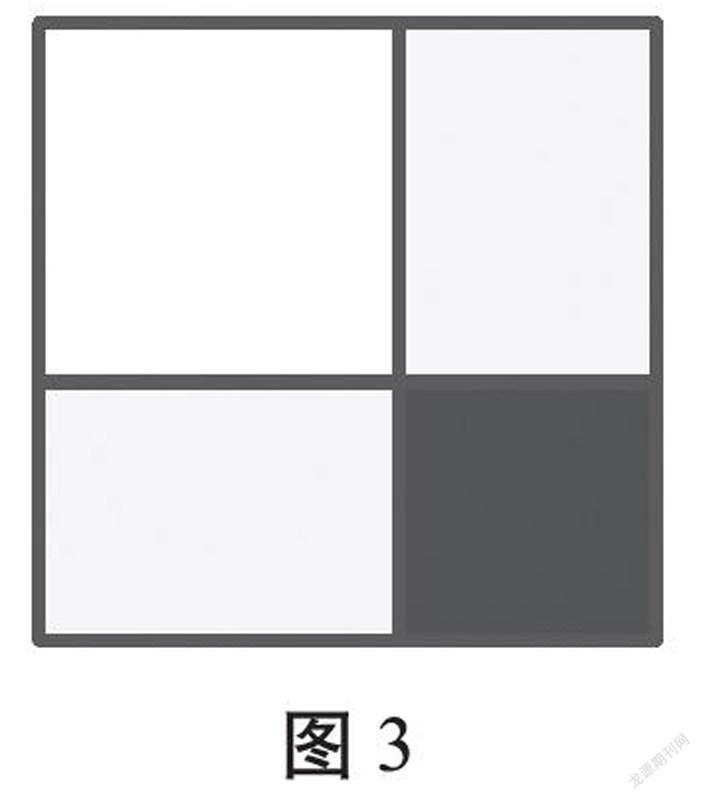
例如，在解决“一个正方形花坛，如果把花坛的边长增加6分米，面积就增加156平方分米，求原来花坛的面积”这道实际问题时，如果用代数的思想，就是要“设原来正方形的边长为x”，列出方程（x+6）2-x2=156。这个方程在小学阶段的学生还不太会解，所以我们就想到把题目转化为图形来解决，见图3：发现边长增加6分米，面积增加的是2块浅色部分和1块深色部分的总和，我们可以先求出深色这一块的面积是6×6=36（平方分米），那么面积增加的156平方分米减去深色部分就是两块浅色部分，而这两块浅色部分的面积是一样的，因为长和宽相同，所以（156-36）÷2=60（平方分米）就是一块浅色部分的面积，因为浅色部分的宽就是6，所以长就是60÷6=10（分米），也就是原来正方形的边长，然后用10×10=100（平方分米）就是原来正方形的面积了。从此题可以看出：我们把一道较复杂的实际问题巧妙地转化为图形之后，更加直观，也能帮助学生更容易地理解这个问题，问题的解决也就简单多了。

3.化抽象为具体，善转化

数学的特点之一就是它具有很强的抽象性，把比较抽象的问题转化为比较具体易操作或较直观的问题，那么不但问题容易解决，而且经过不断的“抽象—具体—抽象”的训练，学生的抽象思维能力也会逐步提高。

如“男女生的比为5： 4，则男生比女生多（   ）%，女生比男生少（   ）%”，平时我们在解决这类百分数问题的时候，需要有具体的数量，可是这里没有，很多学生就困惑了，而这道题的突破口就是把5∶4看成具体的数量，只要符合5∶4的要求都可以，比如看成男生5人，女生4人，或者看成男生10人，女生8人。小学阶段很多知识都是不完全证明，其中举例是一种非常常用的方法，把抽象的比例关系转化为具体的人数来解答，学生就自然而然能够解决了。

四、对转化思想的几点思考

以上实例说明转化思想贯穿于小学数学教学的始终。教师要让转化策略在教学过程中呈现，要做到以下几点：

（1）让学生养成预习的学习习惯，精心设计预习作业单，引導学生主动探索如何用已经学过的方法来解决新的问题。

（2）设计探索环节，学生只有发现自己存在困难时，才会主动去探索方法，从而逐步渗透转化思想。只有彰显数学知识的产生过程，才能让学生在知识的获取过程中去经历，通过独立思考和小组互助不断地去体验。

（3）在设计练习时要注重设计关于思想方法的迁移转化类的题型。

现代认知派心理学家布鲁纳认为，掌握学科的基本结构、基本原理和概念，是通向适当“训练迁移”的大道。其实转化正是一种迁移的能力，转化思想的培养可以让学生在日常生活中更具有迁移的能力。

认知同化学习理论中提出：“运用是把已知命题直接转换到类似的新情境中去，有点类似于我们通常所讲的‘练习’。问题解决是指学生无法把已知命题直接转换到新情境中去，学生必须通过一些策略，使一系列转换前后有序。学生已有的知识可能是与问题解决办法有关的，但需经过多次转换，而非直接运用或练习所能解决的。”这充分说明了转化思想在小学数学教学中的重要意义，也就是很多学生遇到“新题”就困惑的原因。

知识点的转化可以沟通知识之间的联系，能有效促进学生相关知识网络的建构，对于如何更好地渗透转化思想，使其串联起小学教学的全过程，还需要不断的思考和实践，这也需要更多的教育教学理论的支持，从而更加深入地研究问题，加深研究问题的深度和广度。

【参考文献】

[1]马国泉.社会科学大词典[M].北京：中国国际广播出版社，1989.

[2]张大均.教育心理学[M].北京：人民教育出版社，2011.

[3]王永春.小学数学思想方法解读[M].上海：华东师范大学出版社.2017.

注：本文系江苏省教育科学“十二五”规划2015年度重点课题“小学数学高效教学的校本实践研究”（编号：B-a/2015/02/045）的研究成果。