火星大气进入轨迹伪谱凸优化设计方法

2022-03-25林子瑞黄翔宇

宇航学报 2022年1期

刘旭，叶松，林子瑞，黄翔宇，李爽

(1.南京航空航天大学航天学院，南京 211106；2.北京航天自动控制研究所，北京 100854；3.北京控制工程研究所，北京 100094)

0 引言

火星大气进入是指探测器进入火星大气层边界到超声速减速伞展开的这一阶段，时间持续约4 min，期间探测器的速度将从5～7 km/s减速到马赫数2.2以下。进入过程中，探测器应满足热流密度、动压、过载等约束以保证顺利开伞，同时也应满足开伞点的高度和经纬度，从而确保后续飞行任务的时间和空间余量。以“火星科学实验室”为例，任务要求减速伞展开时速度为1.4～2.6，动压为250～850 Pa，开伞点高度不低于5 km，过载峰值低于13，热流峰值低于100 W·cm。因此，多约束条件下末端高度最大化问题是火星大气进入轨迹优化的重点之一。

火星大气进入轨迹优化主要采用间接法和直接法。间接法方面，郑艺裕将无约束火星进入末端高度最大化问题的解作为初始猜值，并采用精确罚函数方法将路径约束处理为等式约束后增广到目标函数，进而将路径约束问题转化为无约束问题求解。Long等使用间接法确定火星进入末端高度最大化问题的最优倾侧角剖面为Bang-Bang结构，并且至少切换两次。直接法则直接离散状态量和控制量，将最优控制问题离散为非线性规划问题进行求解，求解方法包括直接配点法、正交配点法(即伪谱法)、凸优化法等。伪谱法包括Legendre伪谱法、Chebyshev伪谱法、Gauss伪谱法以及Radau伪谱法等。直接配点法方面，Zhao等采用广义二分网格布置配点，结合网格细化和稀疏差分技术，将火星进入轨迹优化问题转化为稀疏非线性规划问题后快速求解。

目前，凸优化方法因其具有多项式计算复杂度和理论全局最优性，因而在航空航天领域得到广泛关注，应用场景包括无人机编队飞行、行星着陆、火箭发射和回收、运载器制导等。在大气进入问题方面，Liu等将倾侧角的正、余弦值作为控制量，并引入二阶锥约束，从而将非凸问题转化为凸问题，并采用序列凸优化方法求解。Wang等则引入倾侧角速度作为控制量，实现控制量和状态量解耦，从而消除倾侧角高频振荡。Zhou等则引入多分辨率技术，对均匀节点进行网格细化，提高了凸优化收敛解的数值精度。此外，Sagliano等结合Flipped Radau伪谱法和凸优化方法，采用伪谱离散格式提高问题离散精度，有效地提高了算法的收敛速度。Wang等则基于Radau伪谱凸优化方法，进一步给出根据线性化误差动态调整信赖域大小的算法，提高了序列凸优化方法的收敛性。

以上轨迹优化方法均为确定性优化方法，而面对真实环境中的大量不确定性，确定性优化方法的局限性日益显现。为解决不确定条件下的轨迹优化问题，NASA已经在航空航天领域开展了不确定性量化研究，该方法主要环节包括不确定性建模、不确定性分析和不确定性优化。不确定性建模时，根据概率信息的完备情况，可以考虑随机不确定性和认知不确定性两类，其中随机不确定性的建模可以采用概率论方法，而认知不确定性由于无法准确给出概率密度模型或高阶统计矩的概率信息，因而只能用上下界表示。不确定性分析的主要目的是估算系统输出不确定性分布的期望或方差，常见的方法主要有蒙特卡洛法、敏感度矩阵法、协方差分析法和广义多项式混沌法、随机配点法、响应面法、拉丁超立方采样法等。而不确定性优化的研究主要集中于鲁棒优化和可靠性优化方法，其中鲁棒优化要求在最差工况下仍能满足任务约束并最小化目标函数，而可靠性优化则给出最小化目标函数时违反任务约束的概率。在大气进入轨迹不确定性量化方面，Halder等，Prabhakar等较早开展了相关研究，国内崔平远、李海阳、李爽等人的课题组也开展了相关工作。

大气进入问题建模时通常以时间或能量为自变量，但以时间为自变量时，需要给定或者优化末端时间，问题求解难度较大。而以能量为自变量时，不仅忽略中心天体的自转角速度，导致模型精度损失，同时要求已知末端高度和速度来确定末端能量，因此不适用于末端高度最大化问题。尽管李俊等提出以弧长为自变量建立大气进入模型，但仍需要对末端弧长进行寻优。本文提出以纵向航程角为自变量建立火星进入模型，将末端时间自由问题转化为末端纵向航程角固定问题，并结合Legendre伪谱离散格式和序列凸优化方法，将火星大气进入末端高度最大化问题转化为凸优化问题后求解。

1 问题描述

1.1 火星大气进入模型

假设火星大气相对火星表面静止，且火星为均匀球体，则弹道升力式火星探测器在火星大气中的无动力飞行过程可以用一组微分方程表示：

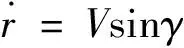
(1)

(2)

(3)

sincoscos)

(4)

(5)

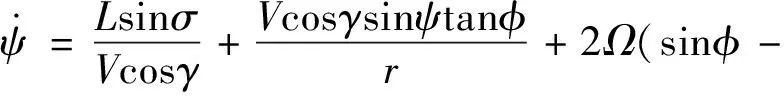
(6)

(7)

式中：、、和分别表示火星探测器的升力系数、阻力系数、参考面积和质量，表示火星大气密度，表达式为：

=e-

(8)

式中：为火星表面大气密度;为飞行高度;为标准大气模型的参考高度;e为自然对数的底数。

火星大气进入问题的典型约束条件包括过程约束和边界约束，过程约束为热流密度、动压和过载约束：

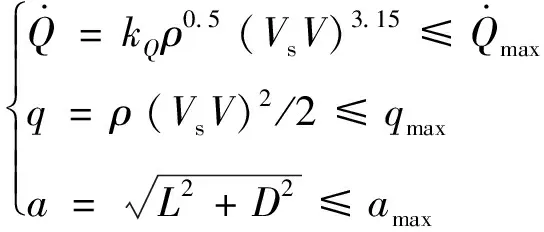
(9)

()=,()=,≤≤

(10)

式中：状态量=[,,,,,],和表示给定的初始和末端状态;和表示各状态量的变化范围上下限。飞行任务一般要求满足全部初始约束，末端约束满足部分即可。

此外,倾侧角的大小和角速度也有一定变化范围,定义控制约束如下:

(11)

(12)

1.2 新的自变量

式(1)～式(6)为常用的大气进入动力学模型，自变量为无量纲时间，但在求解火星进入末端高度最大化问题时需要同时对末端时间进行优化，求解难度较大。此外，常用的模型还包括以负的比机械能(简称能量)=1-2为自变量的模型，但根据其定义可知需要已知末端高度和速度才能确定末端能量，而在火星进入问题中，末端高度和速度在一定区间内即可，而非固定值，因此该模型不适合末端高度最大化问题。同时基于能量的模型需要忽略火星自转才能获得简洁的动力学模型，即假设dd≈，因此动力学模型精度有所下降。

图1 纵向航程和纵向航程角示意图

纵向航程角的初始值为0，末端值则可以根据初始和末端时刻的经纬度确定：

cos=sinsin+coscoscos(-)

(13)

同时，纵向航程角始终单调递增，相对时间的微分表达式也很简洁，因此本文选择作为新的自变量建立火星进入动力学模型。相比基于时间的模型，本文建模方法可以将末端时间自由问题转化为末端纵向航程角固定问题，避免对末端时间进行优化。同时，相比基于能量的模型，不需要事先已知末端高度和速度，也不需要忽略火星自转项，模型精度得以保证。以纵向航程角为自变量的状态微分方程为：

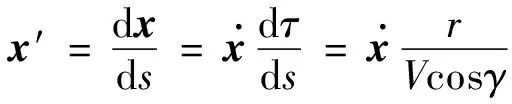
(14)

1.3 状态量扩充

注意到式(14)中不包含飞行时间，因此本文将无量纲时间扩充为状态变量，所以本文方法也可以通过定义时间最优目标函数=来求解时间最优问题。引入飞行时间后，状态量扩展为：

=[,,,,,,]

(15)

此外，选择倾侧角的导数作为控制变量可以抑制倾侧角的高频振荡，则状态微分方程可改写为控制仿射形式：

′=()+()+()

(16)

式中：=[,,,,,,,],=dd，而()=[,,…,],()=[,,…,]和()=[ 1, 2,…, 8]的表达式分别为：

(17)

(18)

(19)

因此，火星进入末端高度最大化问题P可以表述为：

(20)

s.t.(9),(10),(11),(16)

(21)

2 伪谱凸优化方法

Legendre伪谱凸优化(Legendre pseudospectral convex programming, LPCP)方法结合伪谱法和凸优化方法，将状态量和控制量在(Legendre-Gauss-Lobatto,LGL)点处离散，并通过Lagrange插值多项式逼近状态量和控制量，从而将状态微分方程和目标函数中的积分运算转化为代数运算，再结合线性化方法，将最优控制问题转化为凸优化问题，最后通过求解凸优化问题得到原始最优控制问题的近似解。本文直接给出LPCP方法的一般步骤，有关Legendre伪谱法和凸优化方法的内容详见文献[9]和文献[35]。

2.1 一阶线性化

凸优化问题是指目标函数和约束条件都为凸函数的最优化问题，而火星进入末端高度最大化问题的非凸性来源于状态微分方程和过程约束。因此，本文采用一阶泰勒展开方法将这两项约束线性化。

首先将状态微分方程(16)在参考轨迹处线性化：

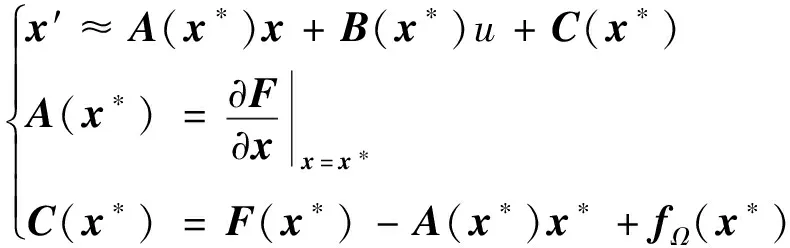
(22)

式中：()中元素(,=1,2,…,8)的表达式为：

(23)

(24)

(25)

(26)

(27)

其余元素均为0，此外：

=-,=

(28)

=-,=

(29)

同理，式(9)中的过程约束可线性化为不等式约束：

(30)

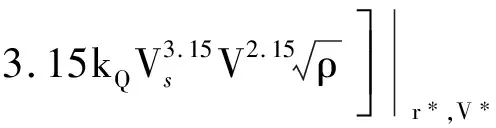
(31)

(32)

(33)

至此，问题P可以近似为连续凸优化问题P：

(34)

s.t.(10),(11),(22),(30)

(35)

2.2 伪谱离散化

一般的序列凸优化(Sequential convex programming, SCP)方法采用均匀节点离散问题，并通过梯形积分处理状态微分方程和目标函数中的积分项。为保证离散精度，通常需要布置较多离散点，因此问题规模较大。而伪谱法将问题在一系列全局正交配点上离散，并通过Gauss积分处理状态微分方程和目标函数的积分项，可以用较少的离散节点保证离散精度。本文采用Legendre伪谱离散格式将问题在LGL节点处离散。

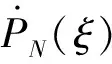
(36)

式中：()为Lagrange插值基函数,且有：

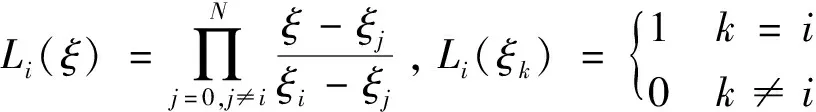
(37)

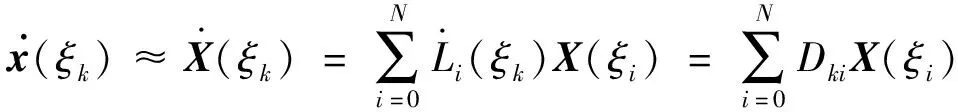
(38)

(39)

由此可将状态微分方程转化为+1组在LGL配点处的等式约束，但需要注意先将问题P的定义域变换到区间[-1,+1]内：

(40)

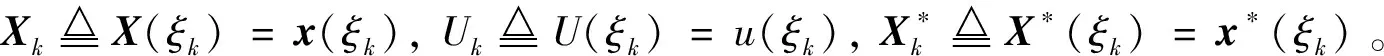
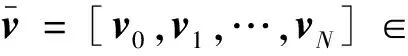
(41)

为了保证算法收敛时虚拟控制尽可能小，需要在目标函数中施加惩罚项：

(42)

式中：为给定的虚拟控制惩罚权重，且惩罚函数选择1范数是为了让虚拟控制中具有尽可能多的0元素，也可以选择2范数作为惩罚函数，即保证全部元素尽可能地趋近0。

注意到问题P的目标函数中并不含有积分项，因此并不需要进行处理。若含有积分项，可使用Gauss-Lobatto求积公式进行近似。

1.3.5 记录手术时长、术中液体出入量和术中发生不良反应如低血压、低血氧、牵拉反射引起的牵拉痛、恶心、呕吐的例数等。

(43)

式中：Δ为给定的信赖域半径。

最后，算法收敛时，应满足前后两次迭代的解差别不大，同时虚拟控制足够小，则可以定义收敛标准如下：

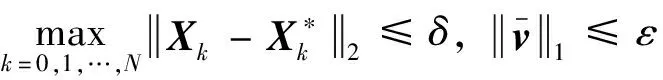
(44)

式中：和为给定的收敛标准。

注意到过程约束、以及状态量或控制量相关的约束不涉及微分或积分项，因此离散化后约束表达式不变，只需将连续变量改为相应的离散变量即可。

至此，离散Legendre伪谱凸优化问题P可定义为：

(45)

s.t.(10),(11),(30),(41),(43)

(46)

2.3 序列凸优化

综上所述，Legendre伪谱凸优化算法的具体步骤为：

3 仿真校验

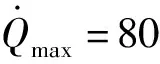
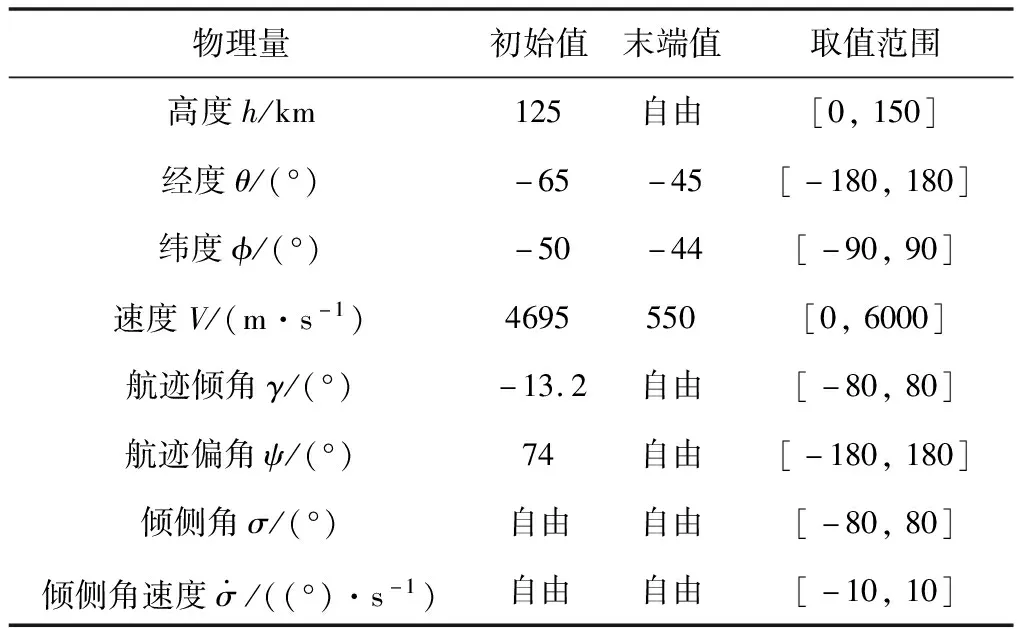
表1 仿真参数设置

根据上述仿真参数，对比了本文LPCP方法、自适应伪谱法、以及施加虚拟控制的SCP方法。其中LPCP设置56个离散节点，SCP设置201个离散节点，二者的初始猜测轨迹均为-35°常值倾侧角积分所得轨迹，惩罚权重=1×10，信赖域半径Δ=0.5，收敛标志=0.05，=1×10，且LPCP和SCP均采用Yalmip工具箱和Mosek求解器进行仿真。自适应伪谱法采用GPOPS软件求解，设置求解器为IPOPT，网格收敛精度为1×10。仿真结果如图2～图5所示。

图2 经度-纬度剖面和速度-高度剖面

图3 航迹倾角和航迹偏角剖面

图4 时间-倾侧角、倾侧角速度剖面

图5 过程约束剖面

同时，GPOPS产生的最优轨迹虽然和LPCP、SCP的最优轨迹一致，但倾侧角、航迹倾角和航迹偏角剖面和其余两个方法有一定区别，同时倾侧角速度剖面的振荡也较大。从算法上来说，GPOPS将最优控制问题转化为非线性规划问题，而LPCP和SCP则是通过序列凸优化逼近原始最优控制问题，且离散格式也不相同，因此两类方法近似解存在一定差异。

为了进一步说明本文LPCP算法的优势，表2中给出了三种方法的结果对比。从表2中可知，LPCP的计算耗时最少，为 6.195 s，而SCP和GPOPS分别耗时10.92 s和48.66 s。对比LPCP和SCP，两种方法的差别仅有离散格式不同，且LPCP的离散节点数(56个)远少于SCP的离散节点数(201个)，这表明Legendre离散格式相比于均匀离散格式能够加速算法收敛，同时LPCP的目标函数值(10.868 km)和SCP的目标函数值(10.853 km)非常接近。对比LPCP和GPOPS，二者分别采用Legendre和Radau伪谱离散格式，尽管GPOPS的目标函数值(11.17 km)优于LPCP(10.868 km)，但差距不大，约300 m，而LPCP的计算耗时远远小于GPOPS，这表明凸优化方法比非线性规划方法的计算效率更高，但在寻优能力上略微下降。