伪谱法及其在飞行器轨迹优化设计领域的应用综述*
2015-11-07杨希祥杨慧欣
杨希祥,杨慧欣,王 鹏
伪谱法及其在飞行器轨迹优化设计领域的应用综述*
杨希祥,杨慧欣,王 鹏
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
采用伪谱法进行飞行器轨迹优化设计是近年来的热点研究方向,然而较全面地对各种方法进行综合分析的文献却很少。在对国内外相关文献进行系统研究的基础上,阐述了航空航天领域应用较为广泛的几种伪谱法的基本原理;归纳了伪谱法将连续最优控制问题转化为非线性规划问题的思路和具体步骤;总结了伪谱法在飞行器轨迹优化设计领域的应用情况;对伪谱法及其在飞行器轨迹优化设计领域应用的未来研究方向进行了分析。
伪谱法;飞行器;轨迹;优化设计;综述
(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)
飞行器轨迹优化问题一般为非线性、带有状态约束和控制约束的最优控制问题。求解最优控制问题的数值方法很多,一般分为间接法和直接法[1]。间接法基于Pontryagin极小值原理推导最优控制的一阶必要条件,将最优控制问题转换为Hamilton边值问题,然后通过打靶法等数值方法求解。间接法在早期的飞行器轨迹优化研究中应用广泛[2-3]。直接法无须求解最优性必要条件,而是采用参数化方法将连续空间的最优控制问题求解转化为非线性规划(NonLinear Programming,NLP) 问题,通过数值求解NLP问题获得最优解。根据参数化方法不同,直接法分为两种基本类型:仅离散控制变量的打靶法与同时离散控制变量和状态变量的配点法。由于直接法弥补了间接法的诸多不足,近30年来得到迅速发展,并被更为广泛地应用于飞行器轨迹优化领域[1,4]。
近年来,一类直接配点法——伪谱法 (pseudospectral method)备受关注[5-6]。该方法采用全局插值多项式在一系列离散点上近似状态变量和控制变量,通过引入类似有限差分矩阵的伪谱差分矩阵将微分方程约束转换为代数约束。从插值多项式的角度,伪谱法可称为全局方法,而用分段多项式近似的传统配点方法可称为局部方法。由于伪谱法的配点一般为正交多项式的根,因此又称为正交配点(orthogonal collocation)法。与局部方法相比,伪谱法能够以较小的计算代价获得较高的求解精度,因此在航空航天领域得到广泛应用,包括空间站姿态控制[7]、小推力下航天器轨道转移[8]、月球软着陆轨迹优化、运载火箭轨迹优化[9-10]等,并已在实际飞行中得到应用[7]。
本文对航空航天领域常见伪谱法及其在飞行器轨迹快速优化领域的应用情况进行综述。国外对各种伪谱法进行综合研究的文献并不多见,最近的一篇由Fahroo和Ross发表于2008年[11],而国内尚未见公开发表的相关文献。
1 飞行器轨迹优化问题描述
对于运载火箭、导弹和可重复使用运载器等不同类型的飞行器,轨迹优化问题的目标函数、约束条件和控制变量等各有特点,但都可以描述为一般的最优控制问题:寻找控制变量u(t)∈m,最小化Bolza型性能指标函数[12]
(1)
其中,状态变量x(t)∈n,初始时间t0和终端时间tf(自由或固定)满足:
动力学微分方程约束
(2)
边界条件
φ[x(t0),t0,x(tf),tf]=0
(3)
以及路径约束
C[x(t),u(t),t]≤0
(4)
式(1)~(4)中,函数Φ,L,f,φ,C定义为
Φ :n××n×→
L :n×m×→
f :n×m×→n
φ :n××n×→q
C :n×m×→c
应用伪谱法时,都将最优控制问题的时间区间由t∈[t0,tf]转换到τ∈[-1,1],对时间t作变换
(5)
将式(5)应用于最优控制问题的表达式(1)~(4), 最小化性能指标

(6)
动力学微分方程约束
(7)
边界条件
φ[x(-1),t0,x(1),tf]=0
(8)
路径约束
C[x(τ),u(τ),τ]≤0
(9)
2 轨迹快速优化领域常用伪谱法
伪谱法源于求解微分方程数值解的谱方法。常见的谱方法有三种:Galerkin法、Tau法和配点法,其中谱配点法又称伪谱法[13]。由于伪谱法的配点一般为正交多项式(Chebyshev多项式或Legendre多项式)的根,因此又被称为正交配点法。
飞行器轨迹快速优化领域常见的伪谱法包括:Legendre伪谱法、Radau 伪谱法、Gauss 伪谱法以及Chebyshev 伪谱法。各种伪谱法的不同在于所选取的插值基函数和配点类型不同,如表1所示。

表1 各种伪谱法插值基函数及配点类型
2.1 Legendre伪谱法

τ0=-1,τ1,τ2,…,τN-1,τN=1


(10)
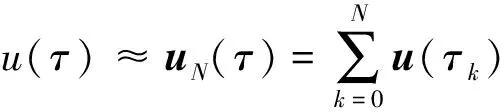
(11)
对于k=0,1,…,N,
(12)
为N阶Lagrange多项式。由Lagrange多项式的性质可得,在配点处,利用插值多项式得到的值和利用动力学微分方程计算所得到的值相等。在第i个配点处,状态变量的导数为
(13)
{Dik}为(N+1)×(N+1)的差分矩阵,且有
(14)
这样,在N+1个配点处,原来连续时间最优控制问题的动力学微分方程约束转换为代数约束,即
i=0,1,…,N
(15)
类似的,性能指标函数转换为
(16)
式中,wi为权重。
边界条件约束转换为
φ[x(-1),t0,x(1),tf]=0
(17)
路径约束转换为
C[x(τi),u(τi)]≤0i=0,1,…,N
(18)
2.2 Radau伪谱法
Radau伪谱法[16-17]的配点采用(-1,1]上的N个Legendre-Gauss-Radau (LGR)点,插值节点由N个配点与初始点τ0=-1构成,即配点数比插值节点数少1个,这也是Radau伪谱法和Legendre伪谱法的不同之处。
状态变量近似表达式为

(19)
这样,在N个配点处,原来连续时间最优控制问题的动力学微分方程约束转换为代数约束,即
i=1,…,N
(20)
{Dik}为N×(N+1)的差分矩阵,且有
(21)
g(τk)=(1+τk)[LN(τk)-LN-1(τk)]
(22)
控制变量近似表示为
(23)
边界控制点可采用样条插值外推得到[18]。性能指标函数转换为
(24)
边界条件约束转换为
φ[x(-1),t0,x(1),tf]=0
(25)
路径约束转换为
C[x(τi),u(τi)]≤0i=1,…,N
(26)
2.3 Gauss伪谱法
Gauss伪谱法[13]的配点采用(-1,1)上的N-1个Legendre-Gauss (LG)点,插值节点由N-1个配点与初始点τ0=-1构成,即配点数比插值节点数少1个。
状态变量近似表达式为
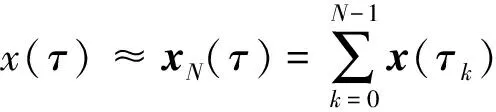
(27)
这样,在N-1个配点处,原来连续时间最优控制问题的动力学微分方程约束转换为代数约束,即
(28)
{Dik}为(N-1)×N的差分矩阵,且有
控制变量近似表示为

(29)
性能指标函数转换为
(30)
边界条件约束转换为
φ[x(-1),t0,x(1),tf]=0
(31)
路径约束转换为
C[x(τi),u(τi)]≤0i=1,…,N-1
(32)
式(28)未定义终端状态xf,终端状态也应满足动力学方程约束,将终端状态约束条件离散并用Gauss积分来近似,可得
(33)
文献[19]从近似精度和计算效率等方面对上述三种伪谱法进行了比较。Radau伪谱法和Gauss伪谱法在状态变量、控制变量和共轭变量的近似精度上均优于Legendre伪谱法,同时,Gauss伪谱法对共轭变量边界值的估计精度高于Radau伪谱法,且在处理含初始和终端约束的问题上具有优势。在计算效率方面,求解相同规模问题时三种方法耗时差别不大。
2.4 Chebyshev伪谱法
和上述三种伪谱法的配点基于Legendre多项式不同,Chebyshev 伪谱法[20-22]的配点基于Chebyshev多项式,采用[-1,1]上的N+1个Chebyshev-Gauss-Lobatto (CLG)点,即
(34)
状态变量和控制变量的近似表达式为

(35)
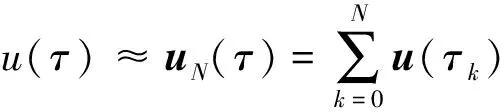
(36)
对于k=0,1,…,N,
(37)
(38)
这样,在N+1个配点处,连续时间最优控制问题的动力学微分方程约束转换为代数约束,即
i=0,1,…,N
(39)
{Dik}为(N+1)×(N+1)的差分矩阵,且有
性能指标函数转换为

边界条件约束转换为
φ[x(-1),t0,x(1),tf]=0
(41)
路径约束转换为
C[x(τi),u(τi)]≤0i=0,1,…,N
(42)
3 轨迹快速优化领域伪谱法应用综述
早在1822年,Fourier就已将谱理论引入微分方程的研究。利用谱方法求解微分方程数值解的思想,可以追溯到1938年Lanczos所做的工作,他建立了选择谱配点法的基函数与配点的理论[23]。20世纪五六十年代,随着Chebyshev多项式应用于初值问题,谱方法再次复苏。20世纪70年代,Gottlieb等首次建立了谱方法的统一数学理论;谱方法的成名源于其在流体动力学领域的应用[24];1972年,Orszag首次将谱配点法称为伪谱法[25]。80年代后期,Vlassenbroeck等首次利用伪谱法求解最优控制问题[20],当时采用的是Chebyshev伪谱法;紧接着,Elnagar等提出了Legendre伪谱法[14];美国海军研究院的Fahroo和Ross等对伪谱法的研究作出了重要贡献,并将其引入飞行器轨迹优化领域[9,22]。
2000年以后,尤其是近几年来,伴随着利用伪谱法求解最优控制问题研究的逐渐增多[6,26],其在航空航天领域的应用研究开始受到重视,并由理论计算发展到地面试验,进而发展到飞行试验验证[7],而飞行器轨迹优化是伪谱法应用最广泛、最成功的领域。Rao等采用Legendre伪谱法研究了高升阻比机动再入飞行器再入轨迹优化问题,并对得到的最优解进行了验证和分析[27];Bollino等将Legendre伪谱法应用于无人飞行器轨迹在线快速生成[28];Fahroo等研究了Legendre伪谱法在可重复使用运载器可达区快速生成问题中的应用,研究结果表明,采用伪谱法可以避免传统求解方法(如能态近似法) 的很多不足,提高求解速度和精度[29];Williams研究了Legendre伪谱法在飞行器地形跟踪轨迹实时优化问题中的应用[30];文献[31]和文献[32]分别采用Gauss伪谱法实现飞机参数近实时辨识和飞机轨迹优化; Ogawa等将进化算法与Gauss伪谱法相结合,解决火箭基组合动力两级入轨可重复使用运载器轨迹优化问题[33]。
2001年以来,麻省理工学院航空航天系对伪谱法进行了系统深入研究,取得了众多研究成果,出版了多篇学位论文。Rea将Legendre伪谱法应用于运载火箭上升段轨迹快速优化问题,分别研究了二维平面内的单级运载火箭轨迹优化问题和三维空间两级运载火箭轨迹优化问题,并用一个预测制导算法研究了采用伪谱法实现在线控制指令生成的可行性,文章同时提出了一种引入二阶差分矩阵减小问题求解规模的方法[34];Clarke将Legendre伪谱法成功应用于通用航空飞行器性能优化[35];Taylor研究了Legendre伪谱法在航天飞机应急下降轨迹优化问题中的应用[36];Stanton采用Legendre伪谱法求解航天器最优转移轨道问题,包括共面转移问题、简单轨道面改变问题和复杂的轨道尺寸/外形/轨道面改变问题,目标函数均选择为燃料消耗最省,仿真结果证明,求解精度和求解效率都能够得到很好保证[37];Benson较系统地研究了Gauss伪谱法,并将其应用于小推力航天器轨迹优化问题和Delta运载火箭上升段轨迹优化问题[38],研究结果表明,与Legendre伪谱法相比,Gauss伪谱法都具有更快的收敛速度和更精确的共轭变量估算结果;Hawkins研究了Legendre伪谱法在月球软着陆轨迹快速优化问题中的应用[39]。
从2007年开始,有关伪谱法在航空航天领域中应用的文章陆续出现在《宇航学报》等国内中文核心期刊中。袁建平教授等将Legendre伪谱法应用于月球软着陆轨迹快速优化问题[40]和空间飞行器有限推力轨道转移优化设计问题[41],研究结果证明,算法具有收敛速度快、对初值不敏感、鲁棒性强等优点;曹喜滨教授则采用Gauss伪谱法解决日-火Halo转移轨道快速优化设计问题[42];杨希祥等研究了Gauss伪谱法在多级固体运载火箭上升段轨迹快速优化和空空导弹最优中制导律设计中的应用,提出采用串行策略进一步提高伪谱法计算效率[43-44];雍恩米等将Gauss伪谱法应用于高超声速飞行器再入轨迹快速优化问题,研究了采用伪谱法在线生成飞行器轨迹时的初值生成问题[45-46];李海阳教授所在课题组对Gauss伪谱法在月球软着陆轨道优化中的应用进行了大量研究[47];此外,杨希祥及其所在课题组对Gauss伪谱法在超空泡水下航行体和平流层飞艇轨迹优化中的应用进行了研究[48-49]。总体来看,国内在伪谱法理论研究方面还不够系统深入,在将其应用于飞行器轨迹快速优化设计领域研究方面正处于快速发展和范围延伸阶段。
4 结论与展望
当前,伪谱法在飞行器轨迹快速优化领域的应用正日益受到重视,根据对国内外研究现状的研究和本文作者们所在课题组的研究工作体会,今后一段时期内,伪谱法及其在飞行器轨迹优化领域应用研究将重点集中在两个方面,一是伪谱法理论的完善研究,二是针对飞行器轨迹快速优化领域的现实需求,深化和拓展伪谱法的应用。
4.1 伪谱法理论深化研究
尽管谱方法用于求解微分方程已有70余年的历史,利用伪谱法求解最优控制问题也已有20多年的历史,但伪谱法理论还有很多方面亟待完善。
1)NLP问题的 Karush-Kuhn-Tucker (KKT)条件与Hamilton边值问题一阶最优必要条件的等价性问题。此问题可转化成NLP问题的最优解是否是原最优控制问题最优解问题,这一问题也是直接法普遍面临的关键问题,很多学者对这一问题的证明做了研究,例如,Benson证明了采用Gauss伪谱法转化得到NLP问题的KKT条件与Hamilton边值问题一阶最优必要条件是等价的[13],同时,证明了节点上满足路径约束即可保证整个过程满足路径约束;Huntington在他的博士学位论文中深化了这一工作[50],但对于Radau和Legendre等伪谱法,这一关键问题的证明尚未进行或完成。
2)配点的选取问题。配点是决定伪谱法求解精度和求解效率的关键因素之一,很多学者仍在对配点的选取问题进行积极研究,例如,文献[51]提出了Legendre 伪谱法的改进形式Jacobi伪谱法,它使用Jacobi多项式寻找配点,Legendre 多项式是Jacobi多项式的子集;文献[52]提出了Hermite-LGL方法,它不使用Legendre 多项式,而是使用分段三次多项式,在LGL点的子集进行配点。随着伪谱法理论的不断完善和数值计算方法的发展,这一方面的研究仍将受到关注。
3)伪谱法中共轭变量的估计问题。共轭变量的精确估计对验证最优控制问题解的最优性、分析状态变量对优化性能指标的敏感度和进行计算网格加细(mesh refinement)是十分重要的。间接法的求解表达式中都包含了共轭变量,因此其解也一般都给出共轭变量估计值。由于直接法不需要构建Hamilton边值问题方程,因此不能对共轭变量进行显式近似,很多学者都一直致力于估计方法的研究[15,53-54],虽然取得了一定成果,但仍未成熟。
4)计算网格加细问题。伪谱法处理最优控制问题的高精度和高效率是在假定问题完全光滑的前提下得到的。但实际的复杂系统状态变量往往是不连续的,或者控制变量是不连续的,或者两者都是不连续的,而且间断点的数目和位置往往是未知的。计算网格加细算法能够检测到间断点的位置和数目,从而大大提高伪谱法解决问题的能力。
伪谱法理论中需要深入研究的问题还包括边界控制量的估计、收敛性证明[55]等。
4.2 轨迹优化领域伪谱法应用深化研究
伪谱法在飞行器轨迹快速优化领域的进一步研究,一是要拓宽算法的应用对象和应用范围,二是要针对轨迹优化中的具体问题应用和改进伪谱法。
1)离线轨迹优化问题。快速、机动发射是现代作战飞行器发展的必然方向。对于采用摄动制导的快速机动发射运载火箭或弹道导弹,需要在射前预先生成一条最优标准弹道,从而完成射击诸元装订。射击诸元的快速装订对缩短发射准备时间具有重要作用,而发射准备时间关系着运载工具的射前生存能力和所运送有效载荷执行任务的快速性,机动发射地点的时变性,对弹道快速优化设计提出了新要求,伪谱法的高计算效率可应对这一挑战,它在这一领域的应用值得关注。高效率和高精度是优化计算不断追求的目标。伪谱法的节点个数是影响计算效率和精度的因素之一,将节点个数同时作为优化问题的设计变量,提高优化效率和精度,是伪谱法求解最优控制问题的研究方向之一[46]。
2)在线轨迹优化问题。轨迹在线生成(快速重规划)是当前飞行器轨迹优化领域的热门研究方向。传统的飞行器制导算法是射前预先计算好一条最优标准弹道,利用一定的制导控制算法,使飞行器克服外界干扰,尽量沿设计的弹道飞行。这样的飞行弹道实际上是次最优弹道。轨迹在线生成技术的引入,使飞行器在因外界干扰作用而偏离设计的最优弹道时,能够快速规划出一条新的最优弹道。简化的、能转化为线性规划的最优控制问题,已经实现了轨迹在线生成,对于只能转化为NLP问题的复杂最优控制问题,实现轨迹在线生成,还有很多问题需要研究[51],伪谱法计算高精度和高效率特点,使其恰恰具有应用于这一领域的潜力。很多轨迹在线生成问题可行域的非凸性,使得任意给定初值条件下,利用伪谱法很难得到最优轨迹,因此初值生成方法成为亟待研究的问题,良好的初值生成方法,将大大减小伪谱法的计算时间[45],从而提高轨迹在线生成速度。
在伪谱法研究方面,国外经历了由理论研究到开展地面试验[56],再到应用于实际飞行的历程[7,57]。在理论研究和数值仿真成熟的条件下,我们也可以有条件地适时设计开展地面试验,以验证理论研究的正确性,并逐步实现其在实际型号中的应用。
References)
[1] Betts J T. Survey numerical methods for trajectory optimization[J].Journal of Guidance, Control and Dynamics, 1998, 21(2):193-207.
[2] Vinh N X.Optimal multiple-pass aeroassisted plane change[J]. Acta Astronautica, 1990, 21(11/12): 749-758.
[3] Vinh N X, Lu P. Necessary conditions for maximax problems with application to aeroglide of hypervelocity vehicles[J]. Acta Astronautica, 1987, 13(6/7): 413-420.
[4] 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J].宇航学报, 2008, 29(2):397-406.YONG Enmi, CHEN Lei, TANG Guojin. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of Astronautics, 2008, 29(2):397-406.(in Chinese)[5] Fahroo F, Ross I M. Convergence of pseudospectral discretizations of optimal control problems[C]// Proceedings of the 40th IEEE Conference on Decision and Control, 2001, 4: 3175-3177.
[6] Gong Q, Fahroo F, Ross I M. Spectral algorithm for pseudospectral methods in optimal control[J]. Journal of Guidance, Control and Dynamics, 2008, 31(3): 460-471.
[7] Kang W, Bedrossian N. Pseudospectral optimal control theory makes debut flight, saves NASA $1M in under three hours [J]. SIAM News, 2007, 40(7).[8] Riehl J P, Paris S W, Sjaw W K. Comparison of implicit integration methods for solving aerospace trajectory optimization problems[C]//Proceedings of AIAA/AAS Astodynamics Specialist Conference and Exhibit, 2006.
[9] Fahroo F, Ross I M, Souza C D, et al. A fast approach to multi-stage launch vehicle trajectory optimizaiton[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, 2003.
[10] Rea J. Launch vehicle trajectory optimizaiton using a Legendre pseudospectral method[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, 2003.
[11] Fahroo F, Ross I M. Advances in pseudospectral methods for optimal control[C] //Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, 2008.
[12] Pietz J A. Pseudospectral collocation methods for the direct transcription of optimal control problems[D]. USA: Rice University, 2003.
[13] Benson D. A gauss pseudospectral transcription for optimal control[D].USA: Massachusetts Institute of Technology, 2005.
[14] Elnagar G, Kazemi M A, Razzaghi M. The pseudospectral Legendre method for discretizintg optimal control problems[J].IEEE Transactions on Automatic Control, 1995, 40(10): 1793-1796.
[15] Fahroo F, Ross I M. Costate estimation by a Legendre pseudospectral method[J].Journal of Guidance, Control and Dynamics, 2001, 24(2): 270-277.
[16] Fahroo F, Ross I M. Pseudospectral method for infinite horizon nonlinear optimal control problems[C]//Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, 2005.
[17] Kameswaran S, Biegler L T. Convergence rates for direct transcription of optimal control problems at Radau points[J]. Computational Optimization and Applications, 2008, 41(1) : 81-126.
[18] Betts J T. Practical methods for optimal control using nonlinear programming[M].USA:Society for Industrial and Applied Mathematics Press, 2001.
[19] Fahroo F, Ross I M. On discrete-time optimality conditions for pseudospectral methods[C]//Proceedings of AIAA/ AAS Astrodynamics Specialist Conference and Exhibit, 2006.
[20] Vlassenbroeck J, Van Dooren R. A Chebyshev technique for solving nonlinear optimal control problems[J]. IEEE Transactions on Automatic Control, 1988, 33(4): 333-340.[21] Elnagar G N, Kazemi M A. Pseudospectral Chebyshev optimal control of constrained nonlinear dynamical systems[J].Computational Optimization and Applications, 1998, 11(2) : 195-217.
[22] Fahroo F, Ross I M. Direct trajectory optimization by a Chebyshev pseudospectral method[J]. Journal of Guidance, Control and Dynamics, 2002, 25(1):160-166.
[23] Lanczos C. Trigonometric interpolation of empirical and analytical functions [J]. Journal of Mathmatics and Physics, 1938(103): 123-199.
[24] Canuto C, Hussaini M Y,Quarteroni A, et al. Spectral methods in fluid dynamics[M].USA: Springer-Verlag, 1988.
[25] Orszag S A. Comparison of pseudospectral and spectral approximations[J]. Study of Application Mathmatics, 1972(51): 689-703.[26] Gong Q, Kang W, Ross I M. A pseudospectral methods for the optimal control of constrained feedback linearizable[J]. IEEE Transactions on Automatic Control, 2006, 51(7):1115-1129.
[27] Rao A V, Clarke K A. Performance optimization of a maneuvering re-entry vehicle using a Legendre pseudospectral method[C]//Proceedings of AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2002.
[28] Bollino K P, Lewis L R, Sekhavat P,et al. Pseudospectral optimal control:a clear road for autonomous intelligent path planning[C]//Proceedings of AIAA Infotech and Aerospace Conference and Exhibit, 2007.
[29] Fahroo F, Doman D B, Ngo A D.Footprint generation for reusable launch vehicle using a direct pseudospectral method[C]//Proceedings of American Control Conference, 2003, 3: 2163-2168.
[30] Williams P. Three-dimensional aircraft terrain-following via real-time optimal control[J]. Journal of Guidance, Control and Dynamics, 2007, 30(4): 1201-1206.
[31] Jorris T R, Mccracken B. Aircraft system identification using pseudospectral parameter optimization wtih adaptive nodes[C]//Proceedings of AIAA Atmospheric Flight Mechanics Conference, 2011.
[32] Bittner M, Fisch F, Holzapfel F. A multi-model Gauss pseudospectral optimization method for aircraft trajecto-ries[C]//Proceedings of AIAA Atmospheric Flight Mechanics Conference, 2012.
[33] Ogawa H, Kodera M, Tomioka S. Multi-phase trajectory optimization for access-to-space with rbcc-powered tsto via surrogated-assisted hybrid evolutionary algorithms incorporating pseudo-spectral methods[C]//Proceedings of 19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, 2014.
[34] Rea J R. A Legendre pseudospectral method for rapid optimization of launch vehicle trajectories [D].USA: Massachusetts Institute of Technology, 2001.
[35] Clarke K A. Performance optimization study of common aero vehicle using a Legendre pseudospectral method [D].USA: Massachusetts Institute of Technology, 2003.
[36] Taylor C P. Optimization study of a trans-atlantic abort for the U.S. space shuttle using a Legendre pseudospectral method [D].USA: Massachusetts Institute of Technology, 2003. [37] Stanton S A. Optimal orbital transfer using a Legendre pseudospectral method[D].USA: Massachusetts Institute of Technology, 2003.
[38] Benson D. A Gauss pseudospectral transcription for optimal control[D].USA: Massachusetts Institute of Technology, 2005.
[39] Hawkins A M. Constrained trajectory optimization of a soft lunar landing from a parking orbit[D].USA: Massachusetts Institute of Technology, 2005.
[40] 罗建军, 王明光, 袁建平. 基于伪光谱方法的月球软着陆轨道快速优化[J]. 宇航学报, 2007, 28(5) : 54-57.
LUO Jianjun, WANG Mingguang, YUAN Jianping.The Legendre pseudospectral method for rapid lunar soft-landing trajectory optimization for hypersonic reentry vehicle via Gauss pseudospectral method [J]. Journal of Astronautics, 2007, 28(5) : 54-57.(in Chinese)
[41] 涂良辉, 袁建平, 罗建军. 基于伪光谱方法的有限推力轨道转移优化设计 [J]. 宇航学报, 2008, 29(4) :1189-1193.
TU Lianghui, YUAN Jianping, LUO Jianjun.Optimal design of orbital transfer with finite thrust based on Legendre pseudospectral method[J]. Journal of Astronautics, 2008, 29(4): 1189-1193.(in Chinese)
[42] 曹喜滨, 张相宇,王峰. 基于Gauss伪谱法的小推力日-火Halo轨道转移优化设计[J]. 宇航学报, 2013, 34(8): 1047-1054.
CAO Xibin, ZHANG Xiangyu, WANG Feng.Optimization of low-thrust transfer trajectory for the sun-mars Halo orbit based on Gauss pseudospectral method [J]. Journal of Astronautics, 2013, 34(8): 1047-1054.(in Chinese)
[43] 杨希祥, 张为华. 基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究[J]. 宇航学报, 2011, 32(1) :15-21.
YANG Xixiang, ZHANG Weihua.Rapid optimization of ascent trajectory for solid launch vehicle based on Gauss pseudospectral method [J]. Journal of Astronautics, 2011, 32(1) : 15-21.(in Chinese)
[44] 杨希祥, 张为华. 基于Gauss伪谱法的空空导弹最优中制导律设计[J]. 国防科技大学学报, 2013, 35(1):28-32.
YANG Xixiang, ZHANG Weihua.Midcourse guidance law optimal design for air-to-air missiles based on Gauss pseudospectral method [J]. Journal of National University of Defense Technology, 2013, 35(1): 28-32.(in Chinese)
[45] 雍恩米, 唐国金, 陈磊. 基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J]. 宇航学报, 2008, 29(6) :1766-1772.
YONG Enmi, TANG Guojin, CHEN Lei.Rapid trajectory optimization for hypersonic reentry vehicle via Gauss pseudospectral method [J]. Journal of Astronautics, 2008, 29(6): 1766-1772.(in Chinese)
[46] 雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究[D]. 长沙:国防科学技术大学, 2008.
YONG Enmi. Study on trajectory optimization and guidance approach for hypersonic glide-reentry vehicle[D]. Changsha: National University of Defense Technology, 2008. (in Chinese)
[47] 彭祺擘, 李海阳, 沈红新,等. 基于Gauss伪谱法和直接打靶法结合的月球定点着陆轨道优化[J]. 国防科技大学学报, 2012, 34(2): 119-124.
PENG Qibo, LI Haiyang, SHEN Hongxin, et al. Lunar exact-landing trajectory optimization via the method combining gpm with direct shooting method[J]. Journal of National University of Defense Technology, 2012, 34(2): 119-124.(in Chinese)
[48] 林明东, 杨希祥, 张为华,等. 无尾舵布局超空泡航行体弹道优化设计[J]. 国防科技大学学报, 2012, 34(6): 116-120.
LIN Mingdong, YANG Xixiang, ZHANG Weihua, et al. Trajectory optimization of planning supported supercavitating flight[J]. Journal of National University of Defense Technology, 2012, 34(6): 116-120.(in Chinese)
[49] 张礼学, 王中伟, 杨希祥, 等. 基于Gauss伪谱法的平流层飞艇上升段航迹规划[J]. 上海交通大学学报, 2013, 47(8): 1205-1209.
ZHANG Lixue, WANG Zhongwei, YANG Xixiang,et al. Ascent trajectory planning for stratospheric airship based on Gauss pseudospectral method [J]. Journal of ShangHai JiaoTong University, 2013, 47(8): 1205-1209.(in Chinese)
[50] Huntington G T. Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D].USA: Massachusetts Institute of Technology, 2007.
[51] Williams P. Jacobi pseudospectral method for solving optimal control problems[J]. Journal of Guidance, Control and Dynamics, 2004, 27(2):293-297.
[52] Williams P. Hermite-Legendre-Gauss-Lobatto direct transcription methods in trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(4):1392-1395.
[53] Herman A L, Conway B A. Direct optimization using collocation based on high order Gauss-Lobatto quadrature rules[J]. Journal of Guidance, Control and Dynamics, 1996, 19(3): 592-599.
[54] Seywald H, Kumar R R. Method for automatic costate calculation[J]. Journal of Guidance, Control and Dynamics, 1996, 19(6):1252-1261.
[55] 黄诘, 张友安, 王丽英. 基于Radau伪谱法的非线性最优控制问题的收敛性[J].控制理论与应用, 2014, 31(2):263-267.
HUANG Jie, ZHANG Youan, WANG Liying. Convergence of nonlinear optimal control problem using Radau pseudospectral method[J]. Journal of Astronautics, 2014, 31(2):263-267.(in Chinese)
[56] Ross I M, Sekhavat P, Fleming A, et al. Pseudospectral feedback control: foundations, examples and experimental results[C]///Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, 2006.
[57] Bedrossian N, Bhatt S, Lammers M, et al. First ever flight demonstration of zero propellant maneuver attitude control concept[C] //Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit, 2007.
Overview of pseudo-spectral method and its application intrajectory optimum design for flight vehicles
YANG Xixiang, YANG Huixin, WANG Peng
Trajectory optimum design for flight vehicles using pseudo-spectral methods has been a hot research direction in recent years, but studies about the overview of this field are very few. Based on the systematic research of domestic and overseas related literatures, the basic principles of several pseudo-spectral methods which have a wide range of applications in aerospace field were expounded; the thoughts and formulas for transforming continuous optimal control problems into nonlinear programming problems were concluded; the applications of pseudo-spectral method in the trajectory optimum design for flight vehicles were summarized; the development directions of pseudo-spectral method and its application in trajectory optimization design for flight vehicles were discussed.
pseudo-spectral method; flight vehicles; trajectory; optimum design; overview
2015-04-01
国家自然科学基金资助项目(11102229)
杨希祥(1982—),男,河北阜城人,副教授,博士,硕士生导师,E-mail:nkyangxixiang@163.com
10.11887/j.cn.201504001
http://journal.nudt.edu.cn
V221; V421.1
A
1001-2486(2015)04-001-08
