天问一号着陆器大底分离安全性分析与验证
2022-03-25崔祜涛
陈 正,崔祜涛,田 阳,饶 炜,董 捷
(1.哈尔滨工业大学深空探测基础研究中心,哈尔滨 150001;2.北京空间飞行器总体设计部,北京 100094)
0 引 言
在经历十个月的星际飞行后,2021 年5月15日天问一号火星探测器在火星乌托邦平原上的预选着陆区成功着陆[1],作为我国首次火星探测任务,天问一号成功实现了火星环绕、着陆与巡视探测[2]。
进入、下降和着陆(EDL)过程是天问一号着陆器成功着陆的关键阶段,在这一过程中,着陆器需在约9分钟的时间里将速度由数千米每秒降至0。在进入过程中,着陆器依靠火星大气进行气动减速,速度将降低90%左右,接着利用降落伞进一步减速,当速度降至约100 m/s时,天问一号着陆器通过反推发动机控制速度进行软着陆。在进入段减速过程中,着陆器需要克服高温和高压,利用防热大底(后文简称大底)来保护着陆器。当降落伞展开,着陆器飞行速度降低后,大底已完成使命,需要被抛离以确保着陆器展开缓冲机构并开启雷达。
为了防止大底与着陆器碰撞,确保大底分离安全性,需要考虑三个方面的因素:首先,大底与着陆器/降落伞系统之间必须有足够的弹道系数差,以使大底下降得更快;其次,当大底与着陆器距离较小时,气动扰动作用会产生吸力将大底推回着陆器[3],火工品必须提供足够的分离速度来克服这种吸力;最后还需要考虑大底和着陆器的相对转动,确保两者不会因旋转而发生碰撞。
大底分离过程中的近距离扰动气动是大底分离问题的重要影响因素,通常通过风洞试验来得到精准模型[3]。作为实施火星探测任务次数最多的国家,美国对大底分离过程气动模型进行了很多研究,文献[4-5]介绍了海盗号亚声速大底分离风洞试验结果,后续的火星探测任务如火星探测漫游者(Mars Exploration Rover,MER)和凤凰号,仍然基于海盗号的风洞测试数据。文献[3]对MER防热大底的近距离扰动气动进行了介绍,展示了大底与着陆器相对距离和马赫数的关系。文献[6]介绍了欧空局火星探测任务ExoMars的大底分离近距离气动扰动风洞试验结果,并与海盗号进行了对比,两者数据吻合较好。徐国武等[7]采用RANS-LES(Reynolds average navier stokes-large eddy simula-tion)混合方法对大底分离体气动特性和背罩分离气动特性进行了数值仿真。
对于大底分离问题,触发方式是另一个重要研究内容,在表1中统计了历次成功的火星探测任务的大底分离触发方式[8-12],在好奇号之前,火星探测任务通过时间触发分离操作。在好奇号任务设计中,考虑到导航误差主要来源于姿态初始化误差,根据导航速度矢量与垂直于速度误差分布平面的单位矢量的点积触发大底分离[12],可以显著降低大底分离速度误差。

表1 历次火星探测任务大底触发方式
在MER任务中,“勇气号”和“机遇号”的任务设计者考虑到防热大底的分离安全性问题,采用了增加重量的方式改变大底的弹道系数,确保大底与着陆器不会重新接触[3],这一措施实际上是在着陆器系统参数定型后的无奈之举。可见深入分析大底分离安全性,选择合适的弹道系数和火工品参数,对火星着陆器设计至关重要。国内外对火星探测EDL技术的研究集中在EDL方案及性能分析[13-14],进入制导方案[15],EDL过程动力学及降落伞动力学[16-17],大底、背罩、降落伞的气动特性研究[7,18-19]等,鲜有针对大底分离安全性的分析研究。
为了分析天问一号着陆器的大底分离安全性,本文提出了一套完整的大底分离安全性分析方法,包括大底分离动力学模型,分离安全性判据,碰撞检测方法,分析了弹射速度、角速度等因素对大底分离安全性的影响,并提出了大底分离触发策略的设计方法,根据可用马赫数和可用时间约束确定累积速度与时间约束触发器的设计参数。最后对天问一号着陆器的伞降过程进行蒙特卡洛仿真并验证大底分离安全性。
1 大底分离过程
这里首先对大底分离前后发生的关键动作进行介绍,为建立大底分离模型及安全性分析奠定基础。
在降落伞展开并稳定下降后,大底分离触发,火工品起爆,其作用力持续到大底脱离连接解锁机构。大底连接解锁机构具有导向功能,在其行程内大底与着陆器的姿态、角速度保持一致,仅有导向方向上的相对运动。
大底分离过程分为短期分离和长期分离,大底与着陆器在近距离气动扰动下的分离过程被称为短期分离,以体轴方向距离Δx达到10D或侧向距离Δz达到3D(D为大底的直径)作为这一过程的结束。随着大底与着陆器之间的气动扰动消失,进入长期分离过程。在短期分离过程中,气动扰动使大底与着陆器有重新接触的可能性,且由于距离较近,两体之间的相对旋转可能造成大底与着陆器发生碰撞。而在长期分离过程中,大底与着陆器/降落伞系统需要足够的弹道系数差,确保大底具有更大的下降速度。
2 大底分离动力学建模与分离过程分析
2.1 动力学模型
我们首先建立大底在连接解锁机构导向行程内的动力学模型。为了便于描述,本文中将大底分离后背罩与着陆平台组合体仍称为着陆器。
由于大底连接解锁机构的导向作用,在分离行程(平行于着陆器体轴)内,大底相对着陆器的姿态保持不变,大底与着陆器只有沿体轴方向的运动,即
(1)
式中:Δr为体坐标系下大底与着陆器的相对位移;rh和rc分别为大底和着陆器在体坐标系下的位置;xrel为着陆器与大底导向距离。
对式(1)求导,可得大底与着陆器的相对速度Δv为
(2)
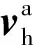
(3)
式中:vh,vc分别为大底和着陆器的绝对速度;ω×为大底与着陆器角速度的叉乘矩阵,由于大底连接解锁机构的约束,两体的角速度相同。
在连接解锁机构约束下,大底与着陆器只有轴向的相对运动,在体坐标系下,相对加速度arel只有轴向分量arel
(4)
考虑相对旋转,大底和着陆器的相对加速度为
(5)
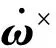
将式(1)、式(2)代入式(5)中,可得大底相对着陆器运动的轴向动力学方程
(6)
式中:ωy,ωz分别为大底和着陆器的角速度在体坐标系的y轴和z轴分量;ahx,acx分别为大底与着陆器绝对加速度在体坐标系的x轴分量。
根据牛顿第二定律,大底和着陆器的绝对加速度可以表示为
(7)
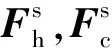
当大底分离触发指令发出后,火工品爆炸,大底与着陆器受到的火工品作用力大小相等,方向相反,均沿着分离行程方向,在体系下为
(8)
式中:Fs为火工品作用力的大小。
则有
(9)
式中:Ah,Ac分别为大底和着陆器受到的轴向气动阻力;Tx为着陆器受到的伞绳力在体轴方向的分量。
将式(9)代入式(6),整理可得
(10)
至此,建立了大底在分离行程内运动的动力学模型。
在分离行程外,大底与着陆器不再有相互作用,可按照单刚体建立动力学模型,这里不再赘述。
2.2 大底分离气动特性分析
气动力在大底分离过程中起重要作用,这里将分别讨论大底、着陆器、降落伞的空气动力学特性。
在大底与着陆器距离较小时,两体之间会产生气动相互作用,对两体的气动力尤其是气动阻力有很大影响。由于大底阻挡了来流,在两体之间的区域形成低压气流,导致着陆器的气动阻力变小,甚至变为负值,也就是说,气流不再阻碍着陆器的运动而是造成向前的吸力。大底的情况则与之相反,在这一过程中大底受到的气动阻力将增大。需要说明的是,气动扰动对法向力和力矩系数的影响较小,对大底的静态稳定性几乎没有影响。在历次的火星探测任务中,任务设计者通过风洞测试来获得精准的近距离扰动气动模型。根据风洞试验结果,近距离条件下大底和着陆器的气动系数由攻角(α)、侧滑角(β)、马赫数(Ma)、轴向距离(Δx)、侧向距离(Δz)决定。
近距离气动扰动的影响会随着大底与着陆器之间距离的增加而减小。风洞测试数据表明,在大底和着陆器的轴向距离Δx达到10D或侧向距离Δz达到3D(D为大底的直径)时,气动扰动现象消失,大底和着陆器的气动环境恢复为自由流域。
大底分离过程实际上是大底与着陆器/降落伞系统的分离,而降落伞气动阻力在着陆器/降落伞系统中占主导地位,比着陆器气动阻力高近10倍。在跨声速流域,由于着陆器与降落伞流场的相互作用,降落伞的气动力会降低。
由于近距离气动扰动和跨声速降落伞气动扰动的影响,在大底分离时大底与着陆器的弹道系数差可能出现负值,不利于大底分离。弹道系数与物体的阻力系数相关:β=m/(CDS),式中m,CD,S分别表示质量、阻力系数、参考面积。
大底和着陆器/降落伞系统均采用零攻角时的阻力系数,以马赫数为横轴绘制弹道系数图,如图1所示。在跨声速区域,着陆器/降落伞系统的弹道系数达到峰值。单独大底(无气动扰动)的弹道系数随马赫数增大而减小,而由于近距离气动扰动,与着陆器距离较近的大底弹道系数会更小,进一步导致两体的弹道系数差减小。因此,高马赫数下进行大底分离,其气动环境是十分恶劣的。
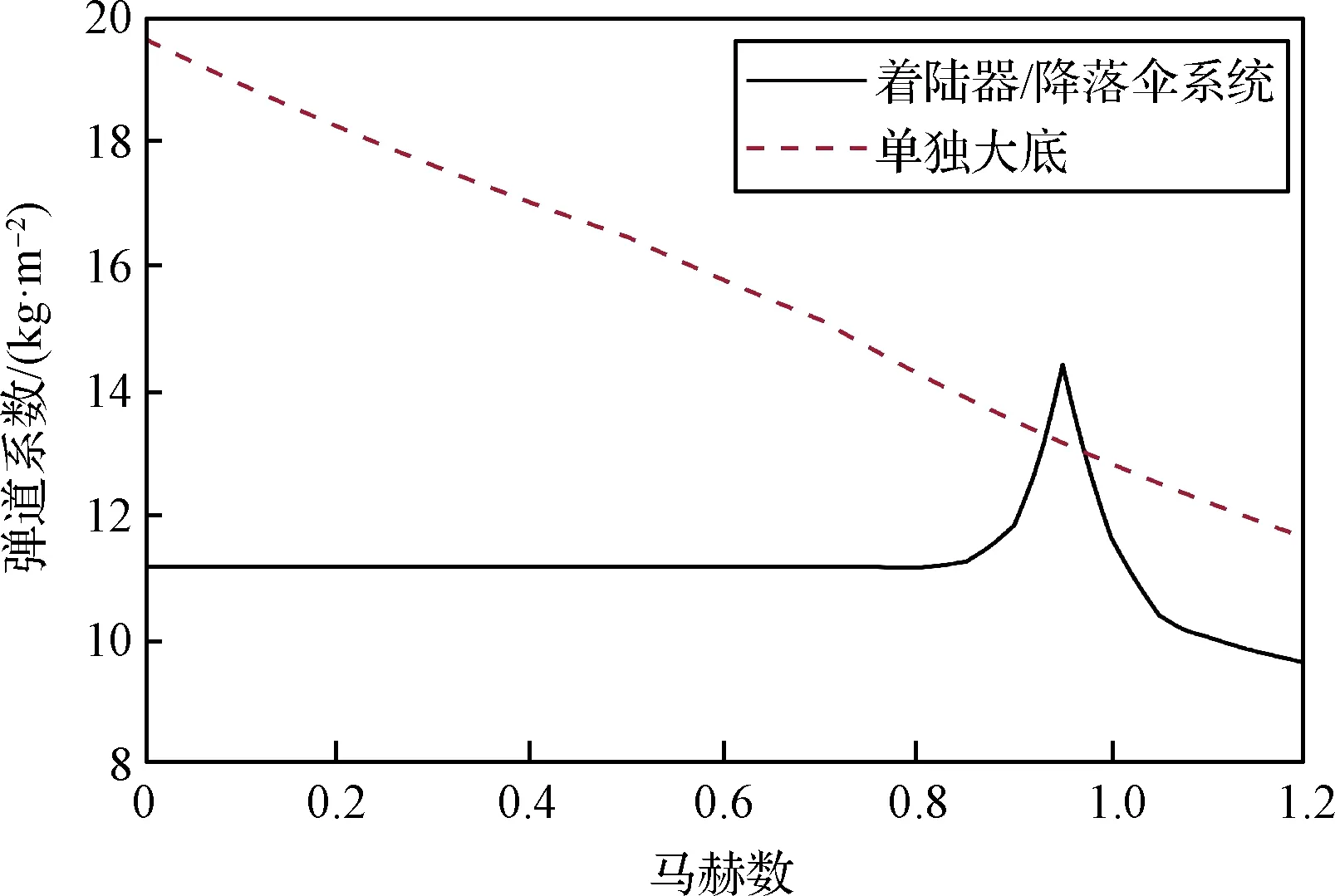
图1 着陆器/降落伞系统与大底的弹道系数随马赫数变化关系
2.3 分离运动特性分析
在建立大底分离过程的动力学和气动模型后,对标称条件下的大底分离过程进行仿真并分析运动特性。
图2和图3展示了分离前后大底和着陆器的姿态和速度。其中图2为着陆器、降落伞和大底的攻角曲线,需要注意的是,降落伞的平衡攻角约为9°,轴对称大底的平衡攻角为零。在大底分离后,着陆器的攻角在降落伞平衡攻角附近波动,而大底的静态稳定性会使攻角趋于零,因此,分离后的相对旋转可能导致大底与着陆器/降落伞系统再次接触。图3展示了着陆器/降落伞系统和大底的火星相对速度曲线,在大底分离时,由于火工品作用,大底速度迅速增加,同时着陆器的速度略有下降,随后由于受到的阻力较小,大底相对着陆器/降落伞系统加速下降。
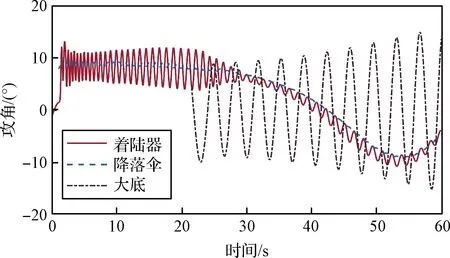
图2 着陆器、降落伞与大底的攻角曲线
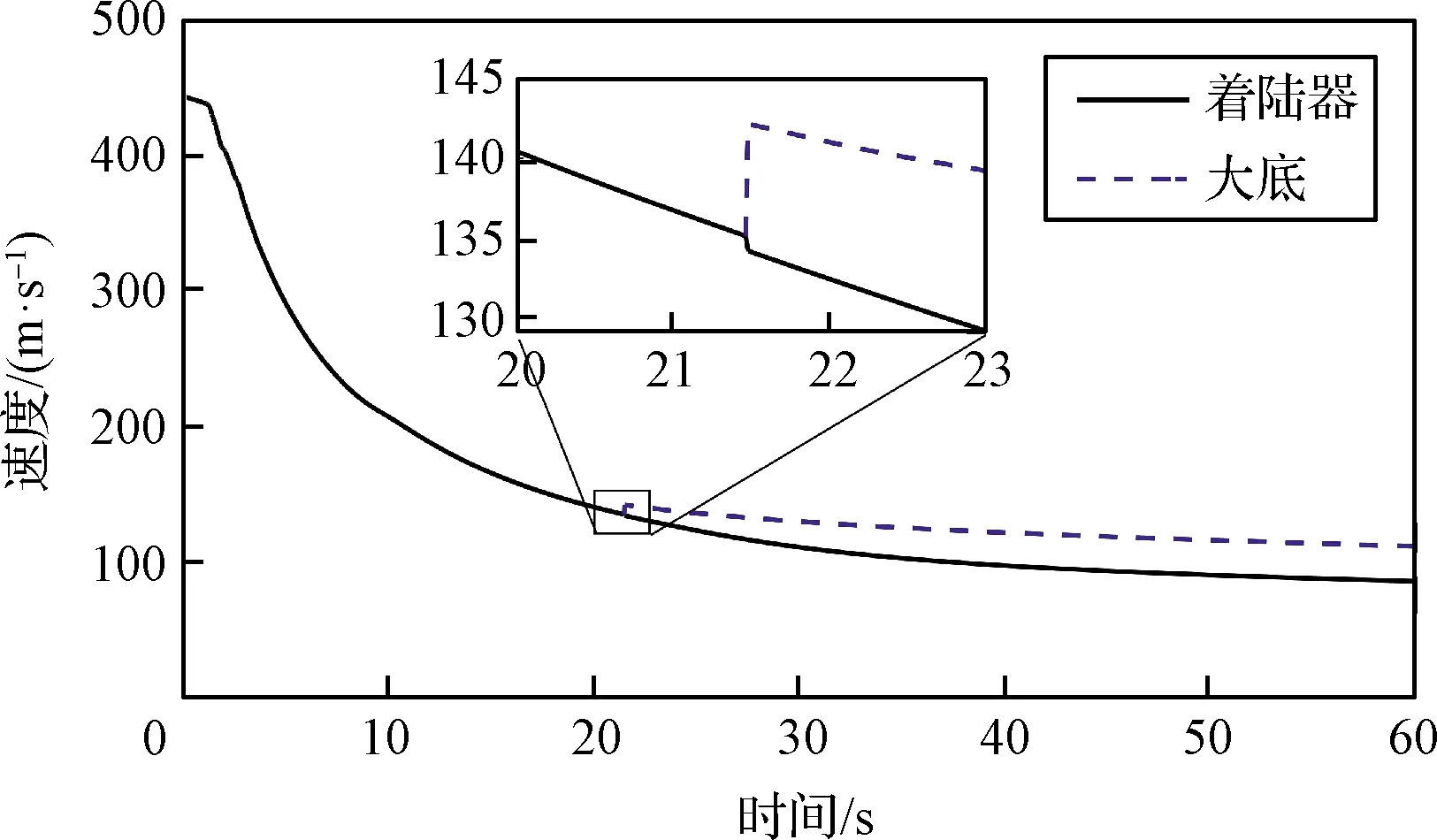
图3 着陆器与大底的速度曲线
3 大底安全分离判据
3.1 安全性判据
大底安全分离是伞降过程中的一项关键动作,不仅要确保大底与着陆器没有重新接触的可能,还要为后续的微波雷达工作以及着陆缓冲机构展开做好准备。因此给出四个安全性判据作为大底分离成功的判断条件,若四个判据全部满足,则认为大底实现安全分离。
判据1:满足无碰撞要求——大底分离1 s内,大底与着陆器不发生碰撞。在大底分离初期,近距离气动扰动较为明显,大底和着陆器/降落伞系统的弹道系数差小于零,在短期分离过程中主要通过火工品造成的弹射速度实现安全分离。
判据2:满足正分离条件——在分离过程中,大底的速度始终大于着陆器/降落伞系统的速度。在长期分离过程中需要确保大底和着陆器不发生重新接触。
判据3:满足微波工作距离要求——在大底与着陆器/降落伞系统分离后10 s,大底与着陆器的距离大于15 m。大底分离之后着陆器会开启微波雷达测量相对火星表面高度及速度,如果雷达工作时大底距离太近,可能会遮挡雷达波束。
判据4:满足留空时间要求——大底分离至背罩分离的时间大于20 s。在背罩分离前需要预留足够的时间进行一系列控制操作。
3.2 大底碰撞检测方法
在判断大底与着陆器是否发生碰撞时,不仅要判断大底与着陆器的质心相对距离,也要考虑大底和着陆器的相对姿态,因此大底和着陆器的形状是不可忽视的。
本文采用射线追踪法来近似计算大底与着陆器之间最短距离,假设由着陆器质心均匀射出密集射线,射线与着陆器和大底外包络相交,两个交点之间的距离为该射线对应距离,所有射线距离的最小值为当前时刻大底与着陆器的最短距离。为了便于射线检测,对大底和着陆器的形状进行一定简化,进入舱的下轮廓被简化为圆锥形,大底的形状被简化为正n棱锥。
通过射线与大底交点形成的点云,可以清晰的看到大底运动过程,如图4所示,随着时间变化,大底逐渐远离着陆器。在这些射线中计算最短距离并按时间绘制最短距离曲线,如图5所示。最短距离曲线单调递增,则表明碰撞风险较低,曲线出现波谷,则表明由于相对旋转,大底和着陆器距离有减小趋势,再次接触的可能性增加,波谷值越小,碰撞的可能性越高。当最短距离为零或负值时,大底与着陆器发生碰撞。需要说明的是,这里所述的最短距离曲线是射线方向上的最短距离,是大底与着陆器之间最短距离的近似,但是在选择足够密集的射线后,并不影响碰撞风险识别和碰撞检测。
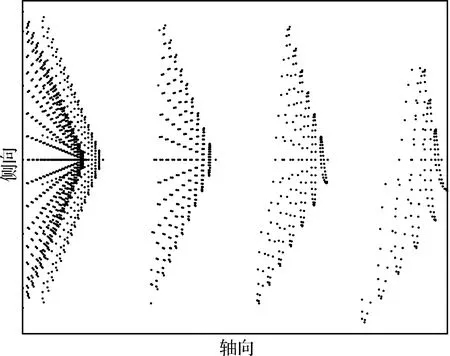
图4 大底形状点云
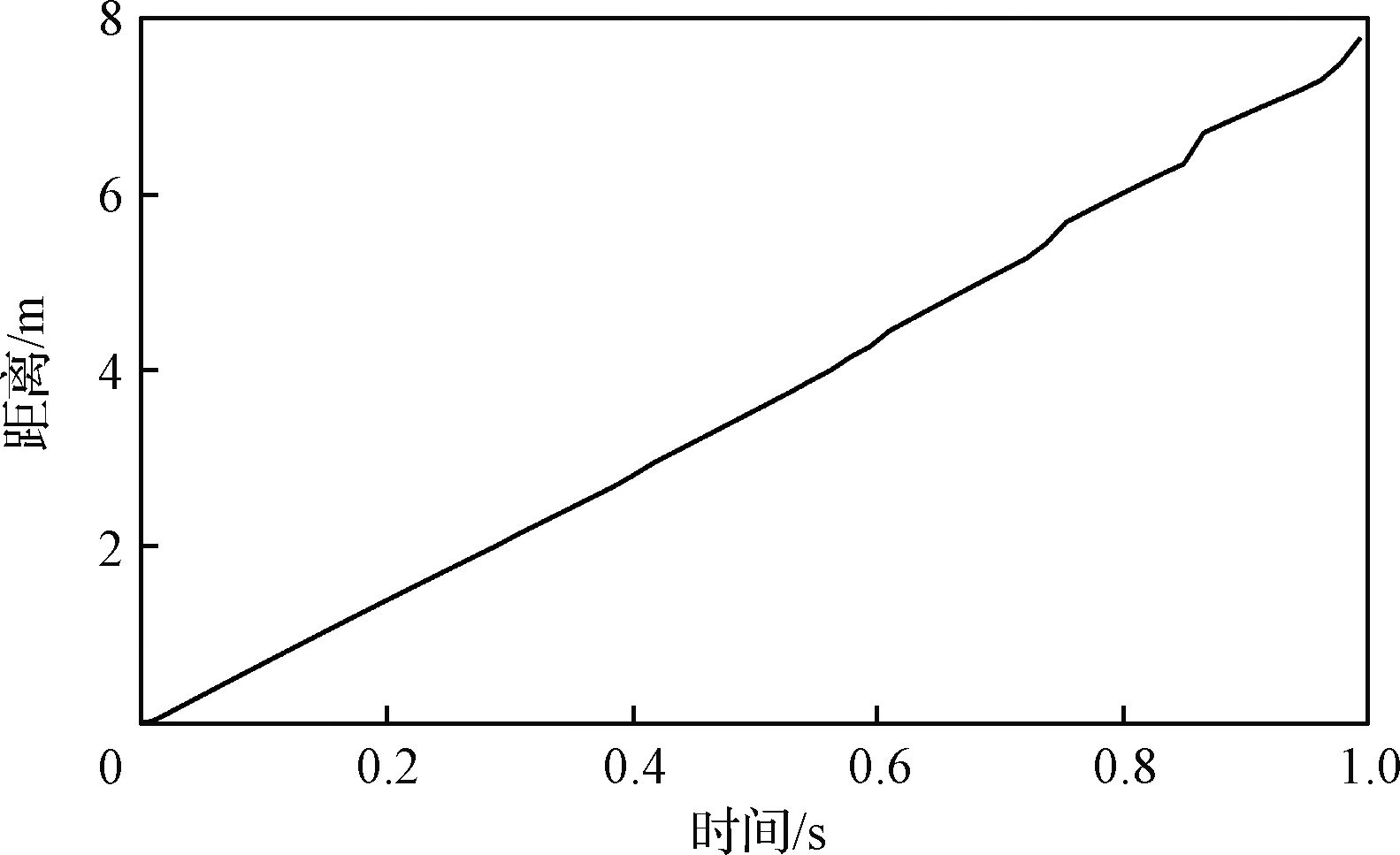
图5 最短距离曲线
4 弹射速度对大底分离安全性影响
大底分离初期大底和着陆器/降落伞系统的弹道系数差可能小于零,需要通过火工品产生足够的弹射速度,确保大底与着陆器正向分离而不会重新接触。
为了确定最小弹射速度,着陆器/降落伞系统和大底的阻力系数在各自偏差范围内分别选取最小值和最大值,对大底分离过程进行仿真,分离触发马赫数取为Ma0.8到Ma1.0,每隔Ma0.1进行一次仿真,共21次仿真。图6给出了仿真中大底与着陆器/降落伞系统速度差的上下边界,其中横轴表示自大底分离后的时间。
在大底开始分离时,由于火工品推力的作用,大底与着陆器速度差迅速增大,分离行程结束后,火工品停止工作,此时的速度差即为弹射速度,如图6中红色星号所示。此后,由于气动扰动影响,两体的相对速度将会降低,需要足够大的弹射速度来确保大底与着陆器的正分离。因此最小弹射速度必须大于最大相对速度衰减值,其中相对速度衰减值是指每次仿真中弹射速度与速度差的最小值的差值。考虑到裕度,最小弹射速度取为
(11)
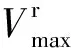
由图6可知相对速度最大衰减了1.35 m/s,考虑裕度,可以选择最小弹射速度为2 m/s。从工程角度考虑,选择更大的弹射速度不仅能够克服气动扰动造成的不利影响,也能使两体迅速分离,降低旋转导致的碰撞可能性。因此在保证结构安全的基础上应当选择更强的火工品,使得弹射速度足够大。
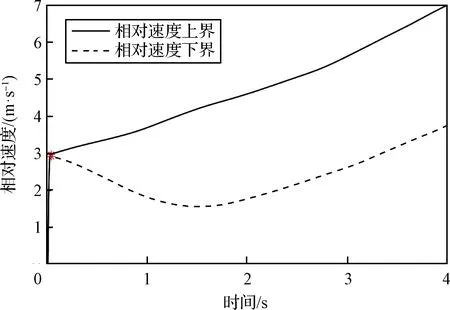
图6 大底与着陆器的相对速度
5 着陆器角速度对大底分离安全性影响
大底分离后,着陆器/降落伞系统的姿态在降落伞平衡攻角附近稳定,而大底的平衡攻角为零,若大底分离状态为高角速度和大攻角,分离后大底将快速旋转,与着陆器之间容易发生碰撞。因此,大底短期分离安全性与大底分离时刻的角速率大小密切相关,为了保证短期分离期间大底与着陆器之间无碰撞,需要在降落伞完全充气后对着陆器的角速率进行阻尼。
在开伞后,降落伞在高马赫数下出现喘振[20](降落伞伞衣不断地收缩和再充气),伞绳力出现大幅度、短周期的振荡,导致着陆器姿态扰动,仿真统计结果表明,喘振造成的最大姿态角速度可达316.45(°)/s。在速度小于Ma1.4后,降落伞喘振结束,着陆器角速度逐渐减小,但若不施加姿态控制,在大底分离时角速度仍会超过120(°)/s,增加大底碰撞的风险。
因此为避免大底和着陆器发生碰撞,在开伞后11 s开始进行姿态控制,三轴均采用角速度阻尼控制,每一轴的控制力矩为
(12)
式中:KD为阻尼系数;ω为角速度;ωD为角速度阻尼阈值,设定俯仰、偏航和滚转通道的角速度阻尼阈值为70(°)/s。
仿真结果表明,姿态控制至少需要持续到开伞后17 s,才能确保角速度控制效果。
6 大底分离触发策略
6.1 可用马赫数和可用时间
可用马赫数、可用时间定义为在当前系统参数的约束下,能够实现大底安全分离的触发马赫数、时间区间。复杂的系统参数导致可用区间无法解析计算,工程设计中,在安全性判据的约束下,通过极限工况和蒙特卡洛打靶的方法确定可用区间的上下限。
根据大底安全分离的四个判据来初步确定大底分离可用区间。可用马赫数区间的下限由大底分离的安全性判据4(留空时间)决定,在低马赫数触发的情况下,留空时间需要大于20 s。考虑到火星环境和着陆器系统参数的不确定性,对各项参数进行拉偏,获得大底分离到背罩分离过程飞行时间最短的极限工况,仿真参数设定见表2。表2中列出的参数囊括了三类不确定性条件:开伞时的着陆器状态不确定性、大气不确定性、降落伞和着陆器气动不确定性,其中开伞点的着陆器状态不确定性由火星进入过程蒙特卡洛仿真统计得到。对这三类不确定性进行分析,确定其中对飞行时间有较大影响的参数并取值。
由于背罩分离的触发条件为火星全球地形数据(MOLA)基准平面的高度0 km,选择最小的开伞点高度、飞行路径角以及最大的开伞点速度,这些参数使着陆器在低空以较大的垂向速度下降;选择最小的气动系数、大气密度和降落伞参考直径,使着陆器受到的气动阻力较小,下降更快;选择最大的垂直风速,使着陆器飞行至0 km的时间更短。除了表2中列出的不确定参数外,其余参数对飞行时间的影响较小,可以取为标称参数。利用上述参数设定进行大底分离仿真,仿真结果表明,若触发马赫数高于Ma0.44(在开伞后29.58 s触发大底分离),留空时间将大于20 s,即可用马赫数的下限为Ma0.44。
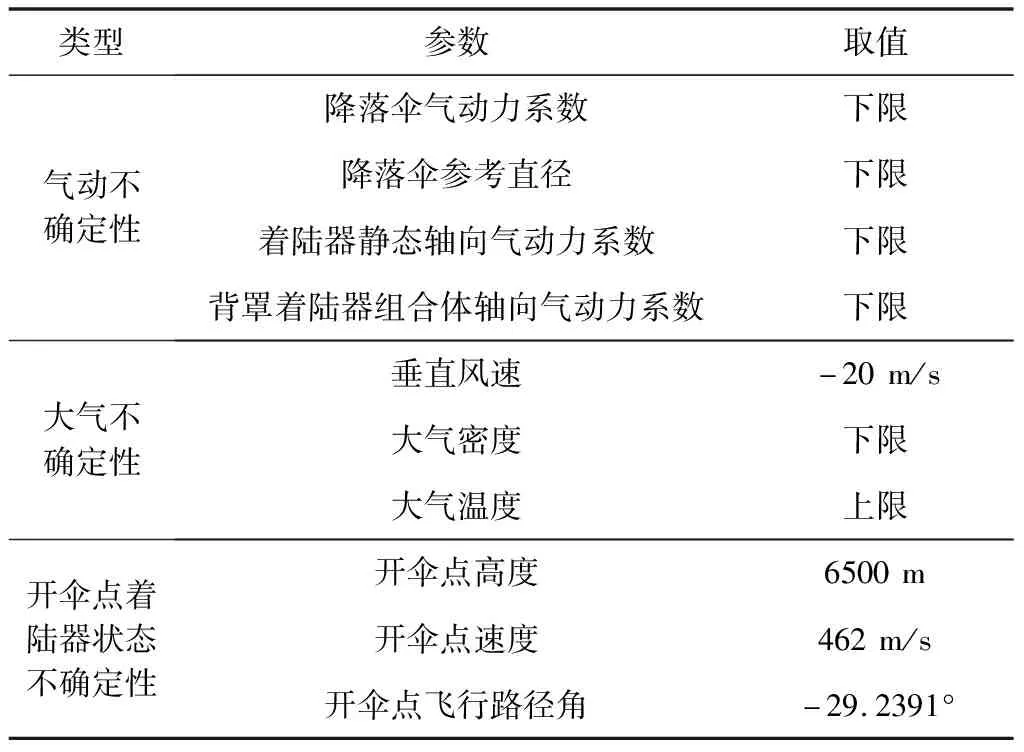
表2 极限工况仿真参数设定
可用马赫数区间的上限由多个因素确定。一方面,触发马赫数要满足安全性判据2(正分离条件)和3(微波工作距离)。而根据图6的仿真结果,在天问一号的系统参数下,大底分离不仅可以满足正分离条件,还能确保大底与着陆器的速度差单调递增,能够满足微波工作距离的要求。另一方面,触发马赫数要满足安全性判据1,避免与着陆器发生碰撞,从无碰撞的要求来看,马赫数上限仍需进一步限制。在不同马赫数下对大底分离进行一组蒙特卡洛仿真,筛选出大底与着陆器最短距离小于0.4 m的弹道,如图7所示,其横轴为每条弹道对应的大底分离马赫数,纵轴为在大底分离后的两体最近距离,选定0.15 m为无碰撞风险的安全距离线,可以看到在此安全距离线下的弹道绝大部分为高马赫下分离,最终选定马赫数的上限为Ma0.8。
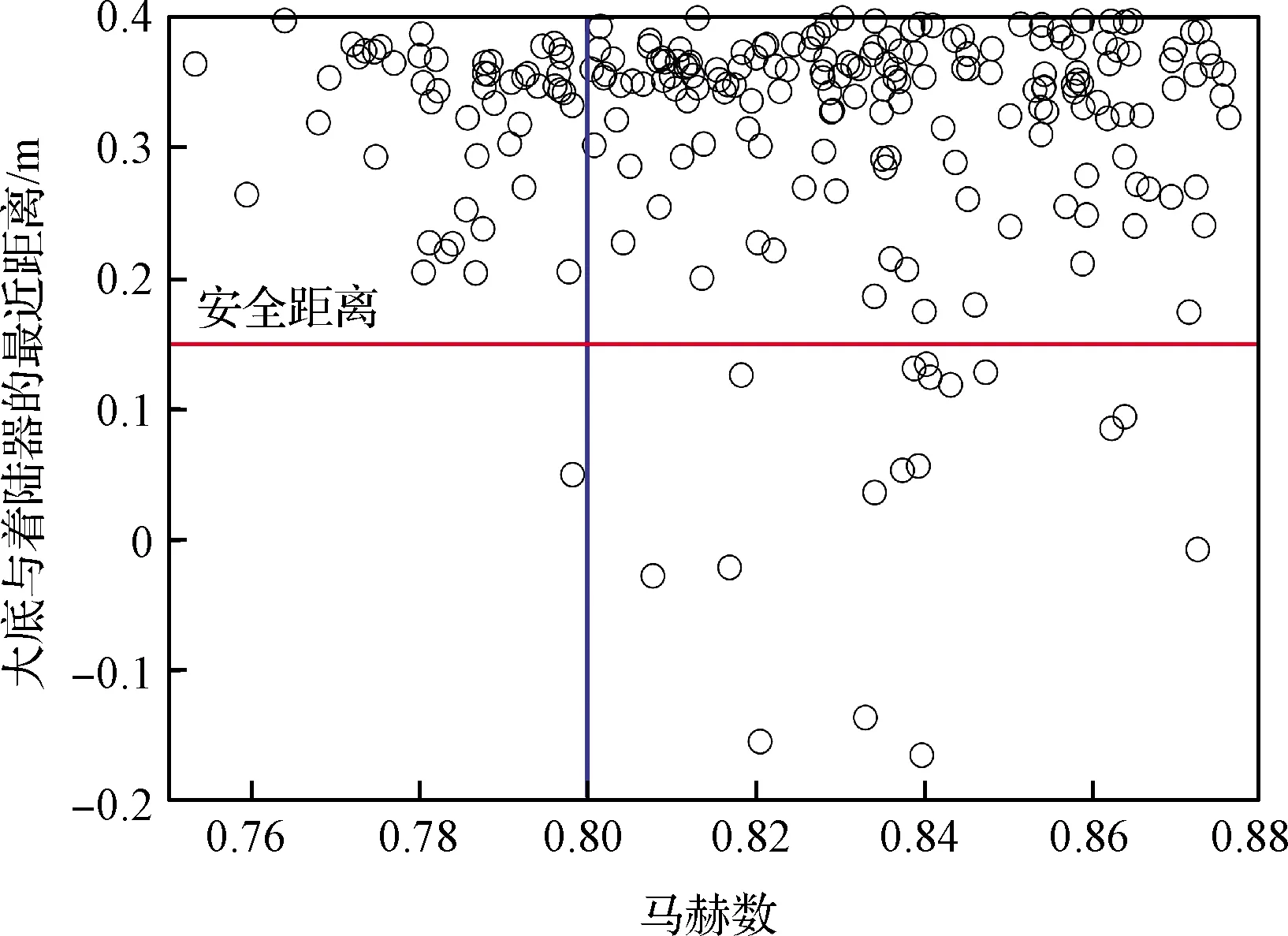
图7 蒙特卡洛仿真中马赫数与最近距离的关系
安全性判据4(留空时间)同样限制了可用时间的上限为29.58 s,为确保姿态控制,可用时间的下限取为17 s。因此,大底分离的可用马赫数区间为[0.44,0.80],可用时间区间为[17,29.58]。
6.2 大底分离触发条件
在EDL过程中,着陆器的飞行马赫数只能采用惯导计算速度和火星大气环境参数间接推算,由于导航速度误差、风速不确定性和声速不确定性的影响,触发马赫数会出现一定波动[12]。
对于火星环境,大底分离触发还面临着另外一个问题。在开伞后,着陆器面临高动态、强振动环境,陀螺仪的姿态估计精度下降,在极端情况下甚至会出现陀螺饱和、姿态估计错误的状况。由于导航速度精度依赖于陀螺仪姿态估计精度,导航速度误差同样会增大。因此天问一号着陆器采用累积速度而非导航速度触发,无需考虑姿态估计误差,提高了极端工况下大底成功分离的概率。累积速度的计算公式为:
(13)
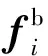
累积速度的分离触发值根据标称弹道来确定,如图8所示,大底分离标称马赫数选择为Ma0.6,对应的标称累积速度为320 m/s,在实际飞行中,由于马赫数曲线、累积速度曲线的波动,触发马赫数会出现一定波动。
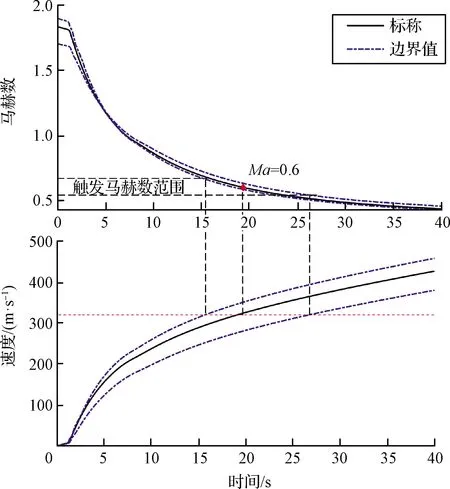
图8 累积速度触发
同时,为了提高分离安全性,对累积速度触发条件施加时间约束,最终大底分离触发策略为:
(14)
式中:t为自开伞后时间;ΔV为开伞后累积速度。
累积速度触发可以消除姿态估计误差对大底分离触发的影响,确保大底在合适的马赫数下触发分离,而时间约束满足了分离前姿控时间要求和分离后留空时间要求。
7 仿真与飞行结果
7.1 蒙特卡洛仿真
对火星伞降过程进行一组蒙特卡洛仿真分析,共2000条弹道。仿真自降落伞开伞开始,到背罩分离结束,开伞点弹道参数见表3,开伞点着陆器状态不确定性由火星进入过程的仿真统计获得。仿真还考虑了火星大气不确定性、气动参数不确定性、降落伞模型不确定性、导航误差等。降落伞动力学借鉴MSL降落伞模拟模型[20]。
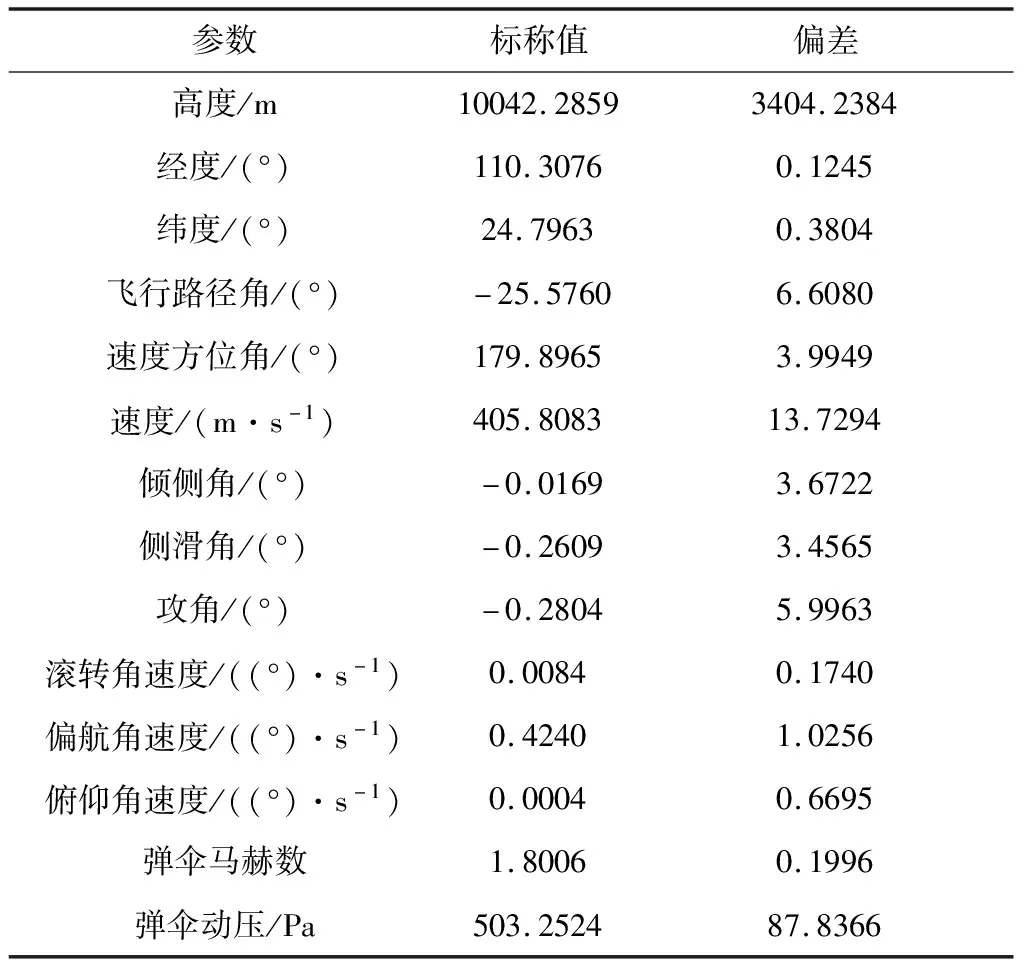
表3 开伞点弹道参数
为了验证大底分离触发条件的安全性,模拟大底分离恶劣工况,将火工品推力等比缩小,使标称弹道的弹射速度为最小弹射速度2 m/s。
对大底触发的时间和马赫数进行统计,见表4,累积速度与时间约束触发策略的时间散布和马赫数散布均在可用区间内,能够满足大底安全分离的要求。
表4 抛大底的时间和马赫数
为判断大底分离安全性,对大底分离成功的四个判据进行了验证,如图9所示。图9(a)为大底与着陆器之间的最短距离曲线的上下边界,以抛大底时刻为零时刻,在这一组蒙特卡洛仿真中,两体之间的最短距离是单调递增的,大底与着陆器没有碰撞风险,满足安全性判据1(无碰撞)的要求。图9(b)为自大底分离至弹伞后40 s内大底与着陆器的速度差的上下边界,以开伞时刻为零时刻,可知在大底结束分离行程后,相对着陆器的速度差是不断增加的,满足安全性判据2(正分离条件)的要求。图9(c)为分离后10 s时大底与着陆器距离统计散布,仿真结果表明最小距离为55.29 m,满足安全性判据3(微波工作距离)的要求。图9(d)为留空时间(大底分离至背罩分离的时间间隔)的散布统计,可见仿真中最小的留空时间为48.91 s,满足安全性判据4(留空时间)的要求。在天问一号着陆器的系统参数下,采用累积速度触发,大底成功分离的四个安全性判据都得到了满足,大底可以实现安全分离。
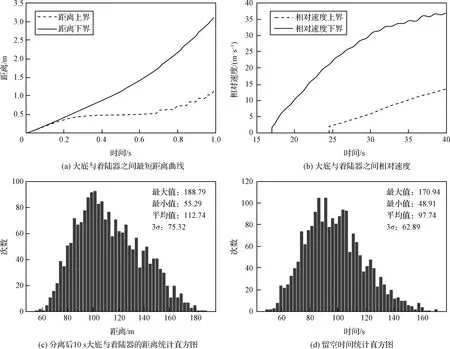
图9 大底分离的四条安全性判据
7.2 天问一号飞行结果
2021年5月15日7时许,天问一号着陆巡视器到达火星大气进入点,开始了约9分钟的火星EDL过程,经过气动减速、伞降减速、动力减速后,着陆器于7时18 分成功软着陆于火星乌托邦平原。在着陆器的伞降减速过程中,降落伞在高度约13 km、马赫数Ma1.8时展开,开伞后20 s,在马赫数Ma0.5左右着陆器开始大底分离。天问一号着陆器的成功证明了大底分离过程的安全性。
8 结 论
针对天问一号着陆器大底分离过程,本文详细分析了天问一号着陆器防热大底分离安全性并设计大底分离策略。通过建立大底分离过程动力学,分析了大底分离过程运动规律,由正分离条件确定了大底分离的最小弹射速度为2 m/s。由于着陆器姿态运动影响分离安全性,利用速率阻尼限制大底分离前着陆器角速率并设定阈值为70(°)/s。结合安全性判据,得到大底分离过程的可用马赫数区间为[0.44,0.80],可用时间区间为[17,29.58],进一步设计了累积速度作为触发条件并施加了时间约束。根据天问一号着陆器设计参数进行蒙特卡洛仿真,结果表明大底分离有足够的安全性。天问一号飞行结果表明,在开伞后20 s、马赫数Ma0.5发出抛大底指令,大底安全分离并成功着陆。本文给出的天问一号着陆器防热大底分离安全性分析过程可以为未来火星探测器的设计与优化提供经验。
