天问一号着陆器EDL过程建模与仿真
2022-03-25崔祜涛黄翔宇
陈 正,崔祜涛,田 阳,黄翔宇
(1.哈尔滨工业大学深空探测基础研究中心,哈尔滨 150001;2.北京控制工程研究所,北京 100094)
0 引 言
作为太阳系中与地球自然环境最为接近的行星,火星一直是人类深空探测的热点之一。对于火星着陆任务而言,进入、下降与着陆(Entry, descent and landing, EDL)过程是直接决定任务成败的关键一环。火星大气密度仅为地球的1%,引力约为地球40%,使得火星着陆器在下降和着陆过程中,既需要气动和降落伞减速,也需要发动机动力减速。着陆器需要依次进行大气进入、伞降减速、动力下降和着陆缓冲才能确保安全软着陆。目前已取得成功的火星探测任务都遵循类似的EDL流程,我国首次火星探测任务天问一号也不例外,于2021年5月15日在火星乌托邦平原成功软着陆。
在火星大气环境存在不确定性的条件下,利用数学模型仿真验证EDL控制策略是着陆器总体及控制系统设计的必要环节。然而火星EDL过程跨越高超声速到亚声速飞行多个阶段,气动特性十分复杂,特别是伞降过程中,柔性降落伞与复杂多刚体相互作用,气动力学环境涉及多种效应,给EDL过程建模带来诸多困难。
针对EDL过程仿真的需求,国内外学者展开了大量的动力学建模与分析工作。文献[4-5]分别针对“火星探路者”(Mars pathfinder,MPF)任务、“火星探测漫游者”(Mars exploration rover,MER)任务,进行了六自由度轨迹分析,研究了着陆器的进入特性。文献[6-7]分别针对“凤凰号”(Mars phoenix)、“火星科学实验室”(Mars science laboratory,MSL)任务,介绍了着陆器的EDL系统设计,并对EDL过程的性能进行分析。对于降落伞动态过程的研究有降落伞的开伞过程、拉直过程中的“绳帆”现象、盘缝带式降落伞充气过程建模、降落伞气动扰动精确建模技术、盘缝带伞的超声速风洞试验等。
在EDL过程分析软件工具方面,NASA开发了POST II(Optimize simulated trajectories II)专用软件,并在“好奇号”任务设计与优化验证中发挥了重要作用。另外,DSENDS是JPL针对深空探测任务EDL过程设计的仿真分析工具,除动力学模拟功能之外该软件偏重定点着陆自主导航控制算法的评估。文献[16]对“火星探路者”下降过程中分别通过弹性吊带、刚性吊索连接的降落伞、后锥体、着陆器三体动力学模型进行了建模。文献[17-18]建立了由降落伞、伞绳和着陆器构成的伞降段的动力学模型,考虑了降落伞开伞、拉直和充气动态过程,并研制了EDL过程的动力学仿真软件。这些研究成果鲜有考虑喘振、卸载扰动等多种气动特性,包含大底、背罩分离的EDL全过程建模与分析研究,也缺乏结合进入与着陆制导策略的弹道仿真分析。
本文结合多刚体和带阻尼的拉伸弹簧模型,建立了降落伞系统模型并利用气动扰动因子对开伞、拉直、充气、喘振、卸载等动态过程气动参数进行了补偿。针对大底、背罩分离过程,建立了考虑连接解锁机构约束的降落伞、着陆器、大底(背罩)多体动力学模型。在此基础上,结合不同飞行阶段的力学环境及制导策略构建了天问一号着陆器EDL全过程高保真仿真模型,通过弹道仿真分析了着陆器和降落伞的动态特性,并与天问一号飞行结果进行对比。本文所建立的EDL高保真模型构建了火星EDL过程的仿真平台,可以为GNC系统设计和验证提供被控对象的数学模型,同时为系统优化论证、总体方案设计、系统参数确定等提供支持。
1 天问一号着陆器模型
天问一号火星探测器系统由环绕器、着陆巡视器(后文简称着陆器)组成。着陆器与环绕器分离后,实施机动离开停泊轨道进入火星大气。
着陆器由气动外罩、降落伞系统、巡视器组成。气动外罩由包围巡视器并起到热防护和气动减速作用的大底和背罩组成,如图1所示。

图1 天问一号气动外罩
天问一号降落伞为锯齿形“盘-缝-带”超声速降落伞,名义面积200 m,伞系总长度近40 m,通过四根吊带与着陆器连接,吊带连接结构如图2所示,四根吊带和降落伞连接带汇交在旋转接口。

图2 天问一号降落伞模型
2 天问一号着陆器EDL过程
根据任务设计,天问一号着陆器将首先利用火星大气进行气动减速。在不到5 min的时间内将进入大气时约25减到1.8。在这一过程中,着陆器通过调整倾侧角改变总升力方向,从而修正飞行轨迹。在马赫数2.8时着陆器配平翼展开,为降落伞展开做好准备。
天问一号降落伞在着陆器速度达到1.8时弹出并展开,进一步消减着陆器速度。随后在马赫数约0.5时防热大底分离,大底分离10 s后着陆缓冲机构展开,测距测速敏感器开始工作,为后续动力下降过程提供位置和速度测量,在减速至约70 m/s后,伞-背罩组合体与巡视器分离。
最终着陆过程包括了动力规避、悬停成像、避障机动、缓速下降和着陆缓冲等操作。着陆器轨控发动机根据自主导航与控制系统给出的指令修正着陆速度和高度,在预选着陆区上空悬停进行障碍检测和着陆点选取,并最终实现安全着陆。
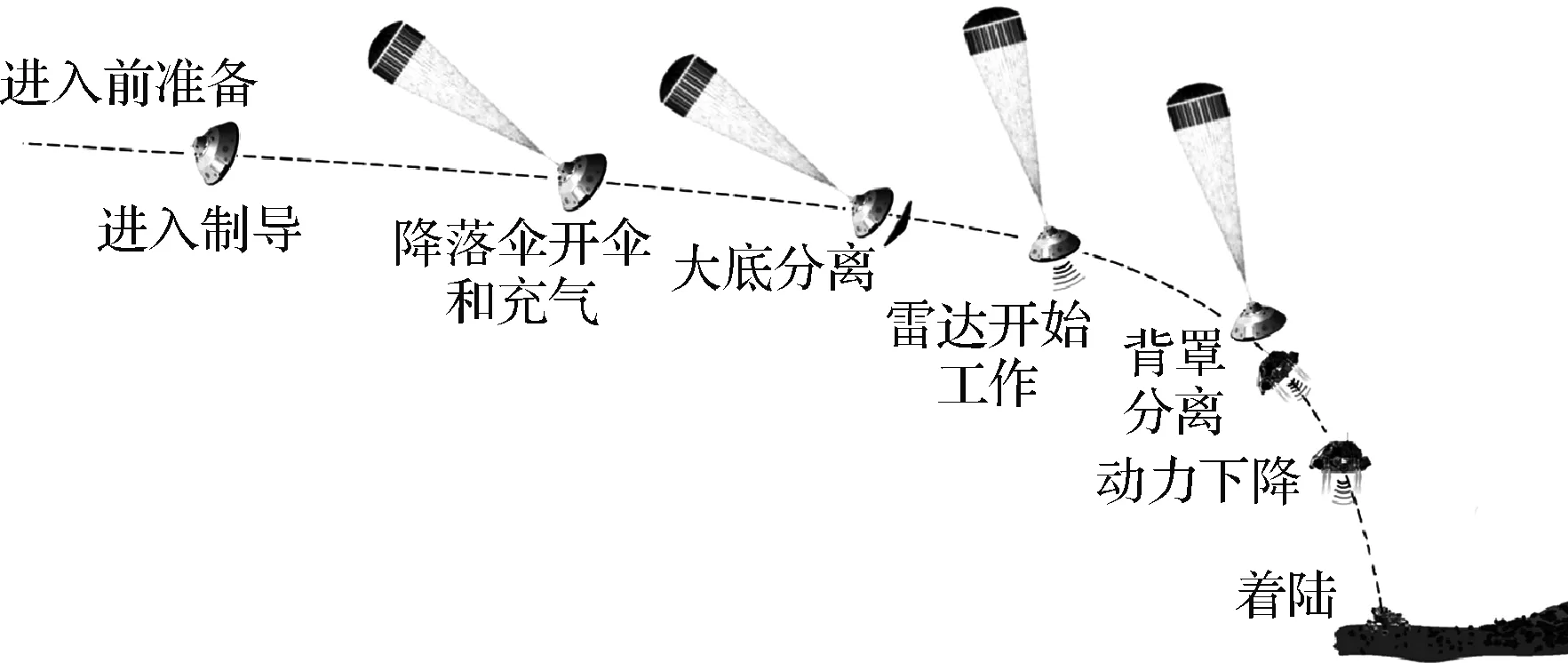
图3 天问一号着陆器EDL过程
3 天问一号着陆器EDL过程动力学
在火星EDL过程中,着陆器按照设计程序执行一系列动作指令,包括配平翼展开、降落伞弹出/充气/展开、大底分离和背罩分离等,使得着陆器的结构、质量特性等发生变化,需要根据不同阶段分别建立动力学模型,并考虑相应的气动特性及扰动。
在整个大气进入过程中,以六自由度刚体动力学模型描述着陆器动力学行为,但要考虑气动参数在配平翼展开后发生的变化。
在伞降段,需要根据不同关键事件建立不同的着陆器动力学模型,如图4所示,右侧为伞降过程各事件,左侧为着陆器和降落伞的模型,虚线为不同阶段所采用的动力学模型。
为了提高仿真效率,在保证计算精度的前提下将降落伞至连接带远端端点的结构统一考虑为刚性整体,如图2所示,其充气、喘振和卸载等动态过程和气动扰动由相应的扰动模型作用在降落伞模型上。
在伞绳达到原长前,忽略伞绳对着陆器的作用力,仍以六自由度刚体模型描述着陆器动力学。伞绳完全拉直后,伞绳力通过弹簧阻尼模型计算,着陆器与降落伞形成组合体。在大底分离且未脱离连接解锁机构的过程中,考虑连接解锁机构约束,构建伞-着陆器-大底组合体动力学。大底完全脱离后,重新利用伞-着陆器组合体动力学模型,但着陆器质量与气动特性均已发生改变。背罩分离过程同样需要根据是否完全脱离分别建立两个阶段动力学模型,包括考虑连接解锁机构约束的伞-背罩-着陆器组合体动力学,以及伞-背罩组合体动力学。
在动力下降过程中,着陆器动力学模型为六自由度单刚体模型。
除动力学模型外,图4中还展示了着陆器和降落伞的力学环境,在第4节中进行详细介绍。

图4 伞降过程动力学模型与力学环境
在具体建立各阶段动力学模型之前给出两个参考坐标系定义。
着陆器体坐标系的原点为着陆器系统质心,轴垂直于圆锥体防热大底的底面,并指向圆锥体顶点;轴指向火星车驶离反方向;轴与轴、轴构成右手直角坐标系,如图1所示。
北天东坐标系原点为着陆器星下点,轴指向火星质心与着陆器连线方向(天向),轴沿火星经线方向指向北,轴沿火星纬线方向指向东。
3.1 着陆器六自由度动力学模型
对于天问一号着陆器的EDL过程,相比于惯性运动,我们更关心的是着陆器与火星的相对运动,将着陆器的惯性加速度表示为:

(1)

在火星惯性系下,由牛顿第二定律可知:
=(+)+
(2)
式中:为着陆器质量;为作用在着陆器上的推力等外力,包括了弹伞作用力和降落伞伞绳力等;为着陆器受到的气动力;为引力加速度矢量。
为了便于计算着陆器受到的外力,着陆器体坐标系下的动力学方程可表示为:
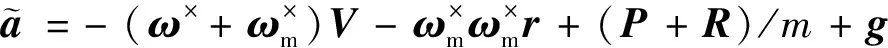
(3)
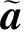
着陆器的运动学方程为:

(4)
式中:为火心距;为火心经度;为火心纬度;、、分别为着陆器的北向、天向、东向的速度分量。
着陆器姿态运动的动力学方程为:

(5)
式中:为着陆器的惯量矩阵;为作用在着陆器质心的外力矩。
描述着陆器姿态运动的方程为:

(6)
式中:、、分别为着陆器的俯仰角、偏航角、滚转角;bu、bu、bu分别为体坐标系相对于北天东坐标系的角速度的三轴分量,角速度可以表示为:
=--
(7)
式中:为北天东坐标系相对火星的角速度。
根据式(3)~式(6)可以构建着陆器的六自由度动力学方程。此外,大底、背罩均为刚体,其六自由度动力学模型与着陆器相同。
3.2 降落伞动力学模型
为进行数值模拟,降落伞的模型应在保证模型精度的前提下尽可能简单,借鉴MSL的降落伞模拟模型,降落伞和连接带被建模为刚体,如图2所示。刚性的降落伞/连接带(后文均称为降落伞)通过四根吊带连接到着陆器后壳,连接带与吊带汇交在旋转接头处。在模型中,旋转接头、吊带的质量均不被考虑,旋转接口只作为几何模型,而吊带模型为仅有拉力的弹性阻尼器。
四根吊带均为无质量的仅受拉力的线性弹簧阻尼器,每条吊带的伞绳力计算公式为:

(8)

降落伞弹射及拉直过程的轨迹和动力学没有详细的建模,而是采用了经验性模型,降落伞拉直的时间为:

(9)

在降落伞拉直时刻,根据着陆器的状态并考虑不确定性,对降落伞模型进行初始化并引入仿真模型。
降落伞的初始化包括了速度、姿态、角速度与位置,其中降落伞质心相对大气的速度为:
=
(10)
式中:为着陆器质心相对大气的速度。
降落伞的姿态有一定的随机性,初始总攻角和速度方位角为:

(11)
式中:T[0°,8°,15°]为服从低限为0°,众数为8°,上限为15°的三角分布随机数;U[0,1)为服从区间[0,1)(不包括1)内均匀分布的随机数。
降落伞的姿态由总攻角和速度方位角确定,同时降落伞的对称轴穿过四个吊带连接点的中心,并确保所有吊带不超过其未拉伸时的长度。其中一根或多根吊带处于拉直状态,既没有松弛,也没有被拉长,其余吊带处于松弛状态。降落伞模型初始化时,其三轴角速度均为0。
降落伞的气动力是伞模型中最复杂的一部分,将在4.2节中详细介绍,需要在稳态气动力系数的基础上考虑马赫数效应、充气、喘振、卸载扰动和喷流扰动的影响。
3.3 伞-着陆器组合体动力学模型
在降落伞拉直后,伞与着陆器之间由四根吊带相连,形成伞-着陆器组合体,其动力学建模过程主要是对伞绳力和力矩进行建模。
四根吊带的形变长度为:

(12)

四根吊带的方向为:

(13)
考虑到坐标系旋转的影响,旋转接口、吊带与着陆器连接点的速度分别为:

(14)

则四根吊带的形变速率为:

(15)
由式(12)和式(15)可以得到吊带的形变长度和形变速率,进而计算着陆器受到的伞绳力:

(16)
着陆器受到的伞绳力矩为:

(17)
在对组合体进行建模时,将降落伞与着陆器均视为刚体,两体之间通过吊带连接,建立12自由度动力学模型。降落伞和着陆器均受到伞绳力作用,伞绳力根据着陆器和降落伞的位置、速度、姿态、角速度计算得到。
背罩分离后的伞-背罩组合体与伞-着陆器组合体的动力学模型是一致的。
3.4 大底-着陆器组合体动力学模型
在降落伞展开后一段时间,大底分离触发,随后伞-背罩组合体与着陆器分离。由于大底(背罩)连接解锁机构具有导向功能,在分离行程(平行于着陆器体轴)内,大底(背罩)相对着陆器的姿态保持稳定,大底(背罩)沿分离行程方向运动。这里将在分离行程内的大底与着陆器运动视为整体运动,通过求解两体沿分离行程方向的相对运动,得到大底-着陆器组合体动力学模型,避免了计算复杂的连接解锁机构约束力。
由相对运动理论,大底与着陆器的相对加速度差可以表示为:


(18)

在体系下,大底与着陆器只有分离行程方向(体轴)的相对运动Δ,取式(18)的第一项即可得到分离方向的相对运动加速度:

(19)
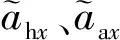
体轴方向的惯性加速度差可以表示为:

(20)
式中:、分别为大底和着陆器受到的轴向气动阻力;为火工品作用力的大小;为着陆器受到的伞绳力在体轴方向的分量。
至此,在分离行程内大底与着陆器体轴方向相对运动的动力学方程可以表示为:

(21)
式中:是气动相对加速度;是火工品作用相对加速度;是引力相对加速度;是伞绳力相对加速度;是牵连相对加速度,各项可表示为:

(22)
由式(21)可以计算大底与着陆器的轴向运动,根据大底与着陆器的合质心状态,可以进一步获得大底与着陆器的运动状态,由质心运动定理可得:
+=
(23)
式中:为着陆器与大底的合质量,即=+;为着陆器与大底合质心的位置矢量。
则着陆器相对火星的速度可以表示为:

(24)

着陆器的位置可以表示为:

(25)
式中:Δ为大底与着陆器的视位置差,在体系下可以表示为[Δ, 0, 0]。
4 着陆器飞行的力学环境
4.1 着陆器气动力
在天问一号着陆器的EDL过程中,着陆器的关键动作使得着陆器的气动环境发生变化,导致着陆器气动特性随之变化。这些关键动作包括了:配平翼展开、大底分离、背罩分离。
在大气进入过程中,为了提供一定的飞行轨迹控制能力,着陆器以约10°的配平攻角飞行,通过调整倾侧角来进行升力控制。在着陆器速度降低后,配平翼展开,着陆器以约0°的配平攻角飞行。
在大底分离后,着陆器与大底距离较近,两体之间会产生气动相互作用,由于大底阻挡了来流,在两体之间的区域形成低压气流,导致着陆器的气动阻力系数变小,甚至变为负值,这一现象持续到两体的纵向距离超过10倍大底直径或横向距离超过3倍大底直径。在这一阶段后,气动干扰的影响消失。背罩分离过程与大底分离过程类似,在背罩与着陆器距离较近时同样需要考虑气动扰动的影响。
4.2 降落伞气动力
降落伞气动特性复杂需考虑多种扰动,不同阶段扰动作用模型如图4所示。
在开伞指令发出后,弹伞筒将降落伞伞包从着陆器中弹射出来,降落伞迅速拉直并过度充气,气动载荷快速增加。在超声速条件下,着陆器与降落伞之间产生气动干扰,使得降落伞伞衣充气形状出现振荡,伞衣不断地收缩和再充气,这种现象被称为喘振(Area oscillations),经过若干次喘振后,伞衣形状逐渐稳定。在这一过程中,降落伞的气动力会出现大幅度、短周期、多次的振荡。
在大底分离或背罩分离时,由于载荷质量的减小,降落伞的突然卸载会导致降落伞背罩组合体气动阻力的骤减,这种现象被称为卸载扰动。
在动力下降过程中,主发动机的羽流会对降落伞的气动流场产生干扰,从而影响降落伞的气动,这种现象被称为主发动机扰动。
在对降落伞气动进行建模时,上述气动现象同样需要考虑。在文献[14]中,将这些现象建模为效应系数,作为降落伞静态气动系数的乘数。效应系数包括:充气系数、喘振系数、卸载扰动系数和主发动机扰动系数。
降落伞的气动系数为:
=()·()·(,)·()·
()·()
(26)
式中:()为降落伞的静态气动系数,只与降落伞的总攻角相关,而不同马赫数下的气动系数需要乘对应的马赫数效应因子();()为充气系数;(,)为喘振系数,在每次仿真时是随机的;()为卸载扰动系数;()为主发动机扰动系数,由主发动机推力决定。
由图5所示可见,通过静态气动系数与充气、喘振系数相乘,很好地体现了降落伞充气和喘振的过程。

图5 降落伞气动系数
4.3 其它作用力
弹伞筒依靠火工品爆炸产生的气流推动伞包,从而使降落伞拉直,弹伞筒会对着陆器产生一定的载荷,持续时间为:
=45+(30·U[0,1]-15)(ms)
(27)
式中:U[0,1]为服从区间[0,1]内均匀分布的随机数。
弹伞作用力大小为:

(28)

大底与着陆器的分离过程中,两体的连接解锁机构同样通过火工品的爆炸来进行分离,四个火工品的作用力、作用时间均不相同,在仿真时各自取10%和10 ms的偏差。
在EDL过程中,着陆器还受到控制力的作用,天问一号着陆器的推力器包括25 N和250 N推力器,通过喷气反作用来进行着陆器的姿态控制,同样可以用来进行小推力的轨道控制。此外还有7500 N变推力主发动机,为着陆器动力下降过程提供动力。
5 EDL制导策略
面对火星高不确定性稀薄大气、弱控制能力、复杂进入约束,天问一号着陆器的大气进入阶段采用了进入终端控制策略(ETPC)控制纵向航程。相比阻力加速度制导、预测校正制导等方法,ETPC具有计算量小、开伞点约束易得到满足的特点,已经在NASA的好奇号和毅力号火星任务中得到了验证。
ETPC策略选取纵向平面内简化的质心动力学模型作为系统方程,着陆器的纵向航程、相对速度、航迹角和火心距为状态变量,纵向升阻比为控制变量,根据小扰动线性化理论将系统动力学方程在标称轨迹附近线性化,再根据边值条件应用最优控制理论可得到进入终端控制制导律如下:
cos=(cos)+()[()+

(29)

大气进入段的横向制导包括倾侧角变号逻辑与航向校正控制。在航程控制阶段,采用倾侧角变号的方式控制横程误差,即当零控横程误差超过横程边界Λ()时,倾侧角变号。在大气进入之初,横程边界设置为常值,之后采用二次函数以使边界收敛:

(30)
式中:、、、、为横程边界参数,根据对横程误差的精度要求以及倾侧角反转情况进行调整。
当相对速度减少至一定值时,航程控制效率低下,制导系统进入航向校正阶段,进一步精细地修正横程残差,航向校正控制律为:

(31)
式中:表示增益系数;表示待飞纵程;表示横程偏差。
动力下降段制导常用方法包括最优燃耗制导、凸优化制导、ZEM/ZEV制导等,但可获得次优性能的多项式制导仍然是火星着陆探测任务首选的制导方法之一。
天问一号着陆器的动力下降过程采用改进的四次多项式制导律,通过控制着陆器姿态并配合主发动机推力调整,使着陆器获得多项式制导给出的期望加速度:

(32)
式中:、、分别为期望位置、速度、加速度;、分别为当前位置、速度;为剩余制导时间。
到达预选着陆区上空后,着陆器悬停并对着陆区进行高精度三维成像,自主选取安全着陆点,随后机动到安全着陆点上方并缓速下降直到着陆,这一阶段的着陆器制导指令为:
=-(-)-(-)+
(33)
式中:,为着陆器当前的速度、高度;,,是期望的加速度、速度、高度。
6 仿真结果与天问一号比较
6.1 弹道仿真与分析
在对天问一号着陆器EDL过程的动力学、力学环境、制导进行建模后,通过弹道仿真对着陆器飞行过程的动态特性进行分析。仿真自大气进入点开始至着陆结束,大气进入点的弹道参数见表1。由于天问一号的着陆点选择在火星北半球平原区域,地表高程相对火星全球地形数据(MOLA)基准平面为-2~-4 km,仿真中选取地表高程为-3 km。
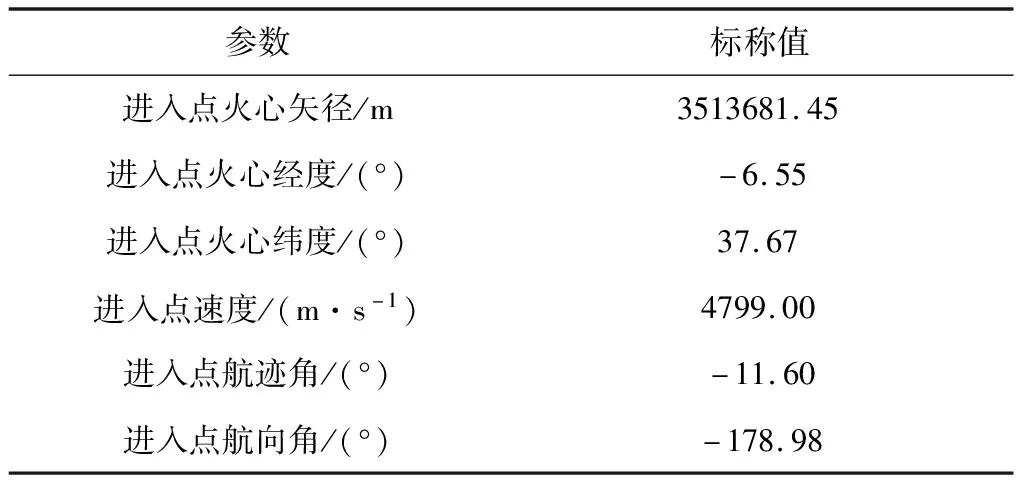
表1 进入点弹道参数
图6、图7分别给出了在EDL过程中着陆器高度、速度的时间历程,经过284.9 s的大气进入过程后,在高度为12.79 km、动压为442.1787 Pa时降落伞展开,此时着陆器的速度为402.8 m/s,经过伞降减速后,着陆器在高度10.01 km、速度137.8 m/s时进行大底分离,在148.7 s后着陆器进行降落伞-背罩组合体分离,随后主发动机启动,着陆器进入动力下降过程,在高度为100 m时开始悬停,接着着陆器将进行避障机动,到达选定的安全着陆点上空,在到达缓降高度20 m后,着陆器以恒定速度1.5 m/s缓速下降。

图6 EDL过程中着陆器高度的时间历程

图7 EDL过程中着陆器速度的时间历程
图8给出了在EDL过程中着陆器总角速度的时间历程,在大气进入过程中,当横向航程误差超出横程边界时,使倾侧角变号以降低横程偏差,在弹道仿真中,倾侧角反转两次,并在配平翼展开后逐渐控制到零,因此在大气进入过程中角速度有三次波动。在开伞后,由于降落伞的喘振,着陆器角速度迅速增大并剧烈振荡,随后逐渐稳定。在伞-背罩组合体分离后,着陆器通过调整姿态控制推力方向,角速度有一定波动。

图8 EDL过程着陆器总角速度的时间历程
图9给出了在EDL过程中着陆器总攻角的时间历程,在大气进入段,为了提供一定的轨迹控制能力,着陆器以约10°的配平攻角飞行,在配平翼展开后,平衡攻角变为0°,通过姿态控制使着陆器攻角稳定在零攻角附近。在降落伞展开后,受降落伞的影响,着陆器无法在零攻角附近稳定,而是在降落伞的平衡攻角9°附近振荡。在伞-背罩组合体分离后,着陆器受控运动,气动的影响较小,总攻角不再是值得关注的参数。

图9 EDL过程着陆器总攻角的时间历程
在EDL过程中,降落伞的主要功能是使着陆器减速,其减速性能可由总伞绳力反映出来。伞降阶段前4 s总伞绳力曲线如图10(a)所示。在弹伞筒弹伞后,伞绳由松弛状态逐渐拉直,这个过程伞绳力为零。伞绳拉直后,由于吊带、旋转接口与着陆器拉紧,伞绳力会出现一个较小的峰值,被称为拉伸力(Snatch force)。随后降落伞快速充气,伞绳力出现第一次峰值力,与降落伞完全充气近乎同时发生,之后降落伞开始喘振直到马赫数小于1.4,在此期间伞绳力剧烈振荡。由于伞衣过度充气,第一次伞绳力峰值力也是整个伞降过程中的最大值,大小为89.75 kN。开伞4 s后的总伞绳力曲线如图10(b)所示,随着速度的降低伞绳力也平稳下降,直到30 s后伞降系统进入稳定下降状态,伞绳力基本稳定在4 kN。在大底分离和背罩分离时,质量骤减,吊带会出现松弛,伞绳力波动并迅速恢复稳定。

图10 EDL过程伞绳力的时间历程
6.2 与天问一号飞行结果比较
天问一号着陆器的EDL过程飞行时间共537 s,其中气动减速段279 s,伞降减速段168 s,动力减速段90 s,开伞高度约13 km,马赫数约为1.8,20 s后,在0.5左右大底分离,在高度约1.3 km、马赫数约为0.25时背罩分离,在高度约为100 m时着陆器保持悬停状态,在高度约20 m时,着陆器以约1.5 m/s的速度开始缓速下降直到着陆,在2021年5月15日7时18分,着陆器成功着陆于火星乌托邦平原南部预选区,着陆精度3.1 km×0.2 km。
在6.1节中展示了天问一号着陆器的弹道仿真结果,EDL过程飞行时间共547.3 s,其中气动减速段284.9 s,伞降减速段168 s,动力减速段94.4 s,开伞时高度为12.79 km,19.3 s后,在马赫数0.59时大底分离,在高度为-1.5 km(此时地表高程为1.5 km)时背罩分离。
弹道仿真结果与真实飞行结果具有较高的一致性。
7 结 论
对于天问一号着陆器的大气进入、伞降减速、抛大底、抛背罩等EDL关键过程,建立了包括着陆器六自由度刚体模型、降落伞-着陆器(背罩)组合体模型、大底(背罩)-着陆器组合体模型在内的动力学模型。结合不同飞行阶段的力学环境及制导策略构建了天问一号着陆器EDL全过程高保真仿真模型,对着陆器的EDL过程进行弹道仿真,分析了着陆器在进入与着陆过程的飞行动态特性。弹道仿真结果与天问一号的飞行结果高度相似,验证了本文EDL模型的准确性。本文建立的EDL高保真模型可以实现火星着陆器从进入点至着陆点的全过程仿真,为未来火星探测器设计与优化提供了仿真平台。
