矩阵伪谱的新定位集及其在土壤生态系统的应用

吴智军，李朝迁

(云南大学数学与统计学院，云南 昆明650504)

1.引言

矩阵伪谱(Pseudospectra)[1]是反映和描述矩阵扰动性的一种工具，也一定程度上反映了矩阵的非正规性的程度，其在马尔科夫链[2]、微分方程数值解的稳定性[3]、动力学[4]、生态学[5]、生物学[6]、信号处理[7]等方面有广泛的应用.

定义1.1[8]设矩阵A = (aij) ∈Cn×n，ε ≥0，‖·‖是向量范数诱导的矩阵范数.称Λϵ(A) ={z ∈C:‖(zI -A)-1‖≥ϵ-1}为矩阵A的ϵ-伪谱，其等价定义如下：

1) Λϵ(A)={z ∈C:z ∈Λ(A+E)，‖E‖≤ϵ};

2) Λϵ(A)={z ∈C:∃u ∈Cn，‖u‖=1，‖(A-zI)u‖≤ϵ}.

进一步，若‖·‖是谱范数，则

3) Λϵ(A)={z ∈C:σmin(zI -A)≤ϵ}，

其中σmin(A)表示矩阵A的最小奇异值，Λ(A)表示矩阵A的谱，即矩阵A所有特征值构成的集合.

矩阵伪谱的理论研究主要包含伪谱的计算和伪谱定位集的确定.伪谱计算的算法有Grid-SVD算法[9]、Krylov子空间迭代算法[10]、块隐式重启Arnoldi 迭代算法[11-13]等.然而对于大型矩阵而言，伪谱的精确计算非常困难[14].另一方面，对于某些应用问题，如连续时间动力系统的鲁棒性[15]等，只需知道伪谱在复平面的大概位置就可以进行判断.这类应用问题研究的需求带来矩阵伪谱另一方面的研究，即矩阵伪谱的定位问题研究.

2001年，Embree 和Trefethen[16]给出基于谱范数的矩阵Gersgorin型伪谱定位集.

定理1.1[16]设矩阵A=(aij)∈Cn×n，ε ≥0，则

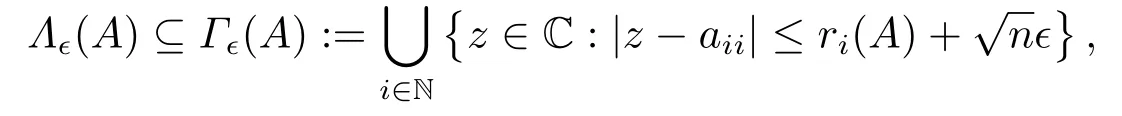
其中

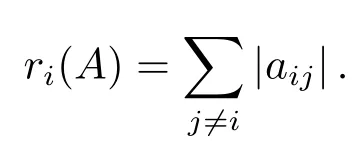
定理1.1只考虑了矩阵行的元素，导致定位结果往往不是很精确.为此，2016年Kostic等[17]同时利用行与列的信息改进了上述结果，得到如下两个伪谱定位集.

定理1.2[17]设矩阵A=(aij)∈Cn×n，n ≥2，ε ≥0，则Λϵ(A)⊆Kϵ(A)，其中

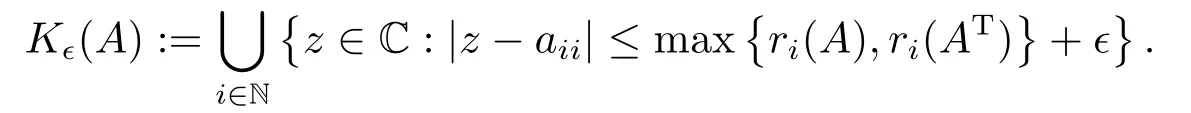
定理1.3[17]设矩阵A=(aij)∈Cn×n，n ≥2，ε ≥0，则

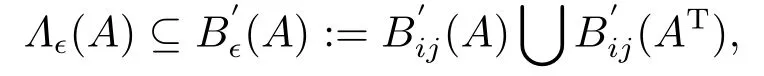
其中

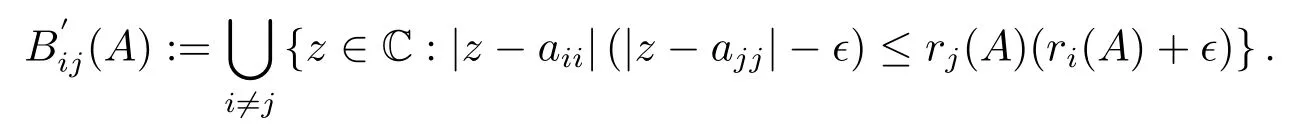
本文将继续研究矩阵伪谱的定位问题，给出了优于文[16-17]中结果的矩阵伪谱定位集，并应用所得结果对土壤生态系统的稳定性进行扰动分析.

2.矩阵伪谱新的定位集

本节，应用矩阵A+E的特征多项式和三角不等式，寻找矩阵伪谱新的定位集.

定理2.1设矩阵A=(aij)∈Cn×n，n ≥2，ε ≥0，则

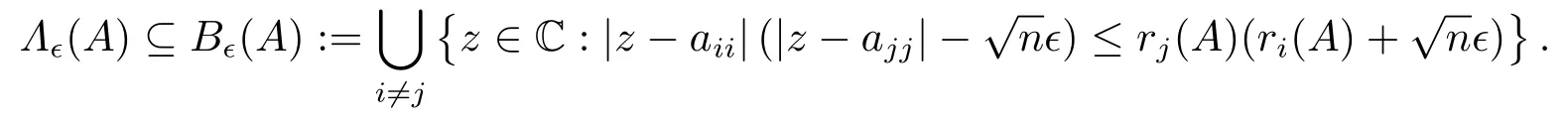
证设λ ∈Λϵ(A)，则存在矩阵E =(eij)∈Cn×n(‖E‖2≤2)，使得

其中x ∈Cn是A+E的对应于λ 的一个非零特征向量.

设

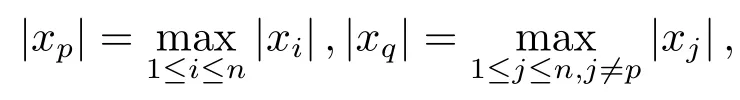
则|xp|≥0.由(2.1)式的第p个等式得

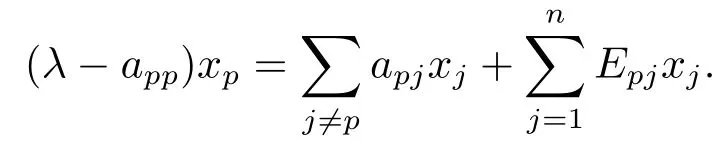
应用三角不等式得

即

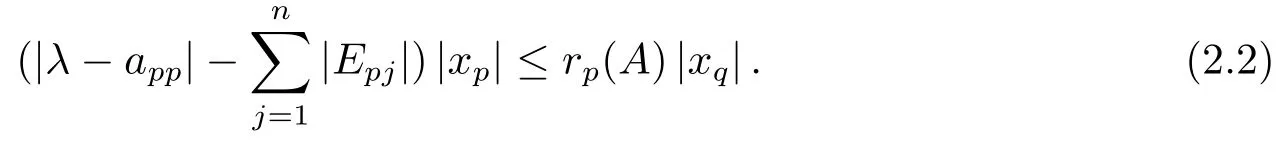
由Cauchy不等式得

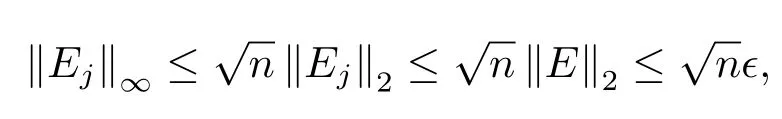
其中，

由(2.2)式得，

若|xq|=0，则于是λ ∈Bϵ(A).若|xq|≥0，则

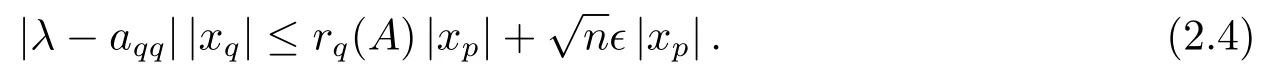
由(2.3)式和(2.4)式得

故

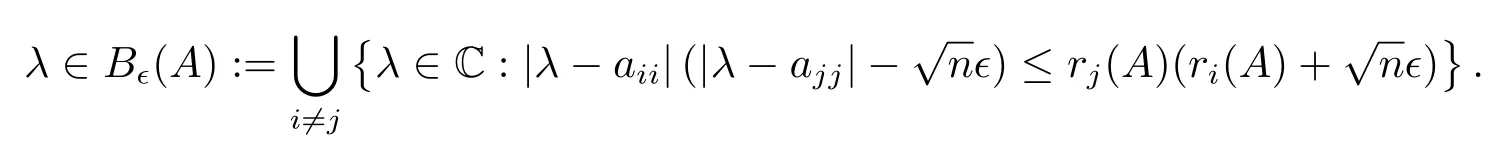
证毕.

注1当ϵ=0时，定理2.1退化为矩阵特征值包含集的Brauer卵形定理，即定理2.1是Brauer卵形定理[18]的推广.

注2定理1.3中的需同时考虑ri(A)和ri(AT)，当ri(AT)大于ri(A)时，定位集往往没有定位集Bϵ(A)精确.

下面给出另一个伪谱定位集.

定理2.2设矩阵A=(aij)∈Cn×n，n ≥2，ε ≥0，则

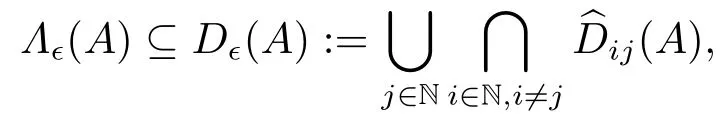
其中

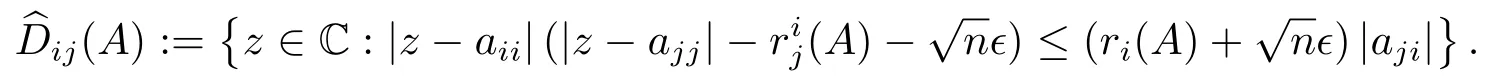
证设λ ∈Λϵ(A)，x ∈Cn是A+E的对应于λ 的一个非零特征向量，类似于定理2.1，设

则|xp|≥0.于是对于任意的ip，(2.1)式的第p个等式可写为

应用三角不等式可得

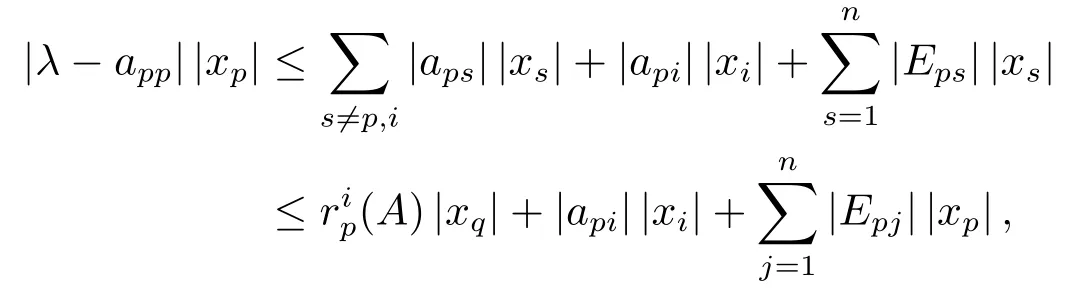
即

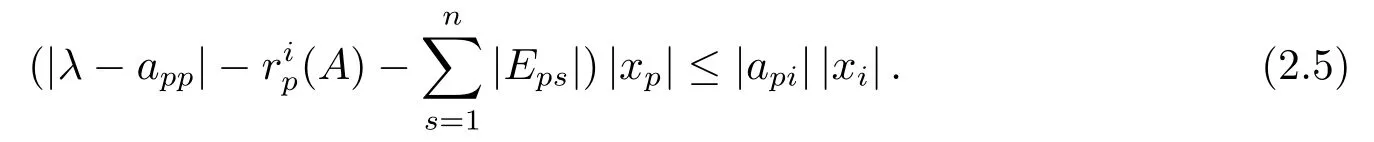
若|xi|≥0，由(2.1)式的第i个等式得

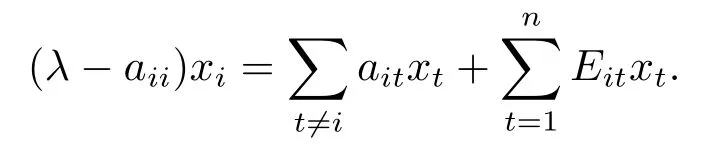
应用三角不等式得

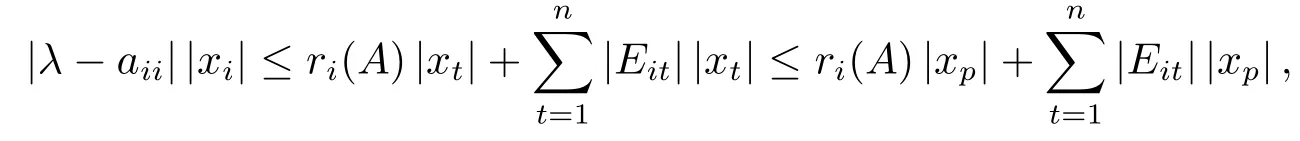
即

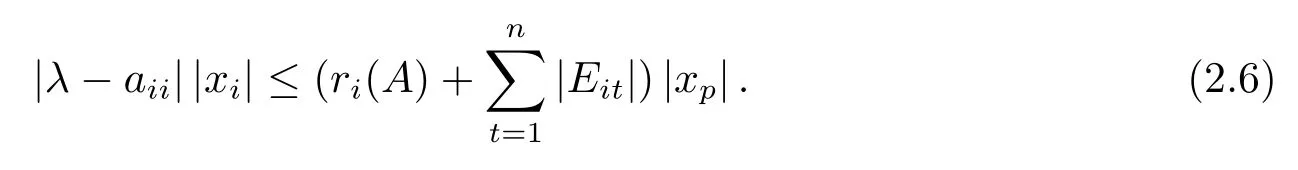
由(2.5)式和(2.6)式得

故

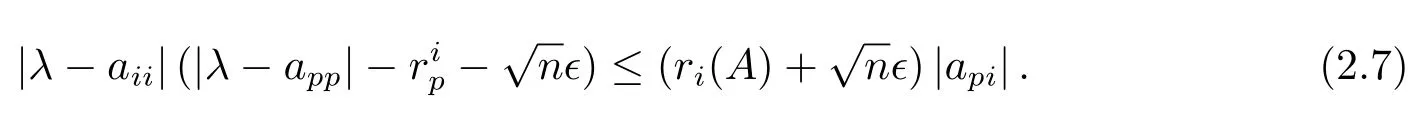
若|xi|=0，(2.7)式显然成立.因此，

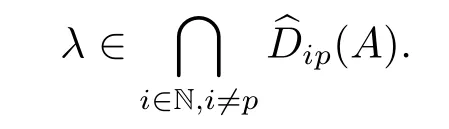
故

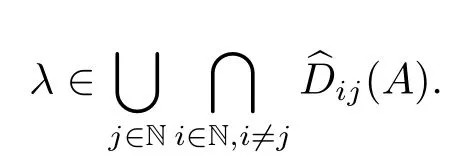
证毕.

注3当ϵ=0时，定理2.2退化为文[19]中矩阵特征值定位定理.

下面给出新的伪谱定位集与文[16]中的定位集之间的关系.

定理2.3设矩阵A=(aij)∈Cn×n，n ≥2，ε ≥0，则

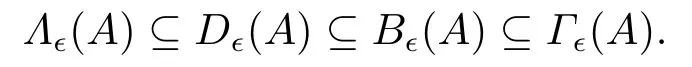
证先证Dϵ(A)⊆Γϵ(A)，设z ∈Dϵ(A)，则∃j ∈N，对任意的ij使得

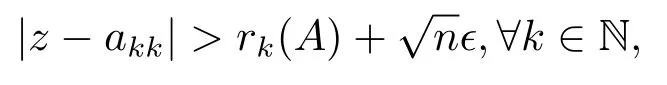
且

因此，

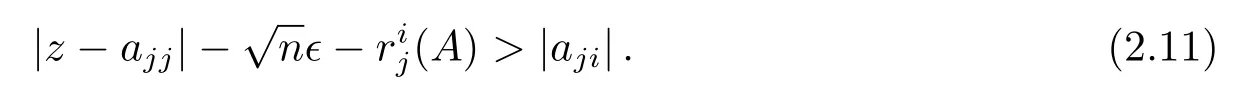
由(2.9)式和(2.11)式得，

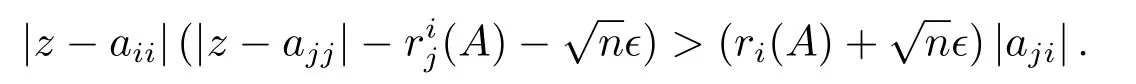
与(2.8)式矛盾，故z ∈Γϵ(A).

类似于Dϵ(A) ⊆Γϵ(A)，易证Bϵ(A)⊆Γϵ(A).下证Dϵ(A) ⊆Bϵ(A).事实上，设z ∈Dϵ(A)，则∃j ∈N，对任意的ij使得(2.8)式成立.由Dϵ(A)⊆Γϵ(A)得，∃i ∈N，使得

由(2.8)式和(2.12)式得

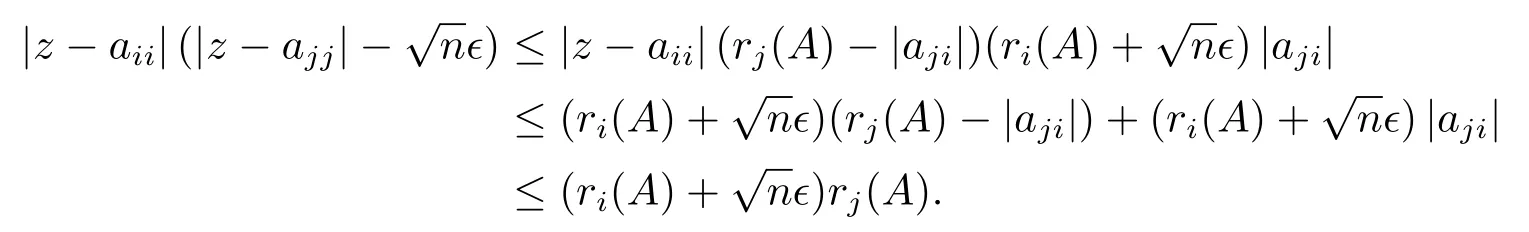
故z ∈Bϵ(A).因此，Λϵ(A)⊆Dϵ(A)⊆Bϵ(A)⊆Γϵ(A).证毕.

定理1.1中的伪谱定位集Γϵ(A)需要确定n个圆盘，而新的伪谱定位集，即定理2.1和定理2.2中的定位集Bϵ(A)和Dϵ(A)需要确定n(n-1)个卵形区域.然而，正如定理2.3所示，新的伪谱定位集Bϵ(A)和Dϵ(A)比定理1.1中的伪谱定位集Γϵ(A)更精确.下面通过数值例子比较新的伪谱定位集与文[17]中的伪谱定位集，即定理1.2和定理1.3中Kϵ(A)和(A) 的优劣.

例2.1考虑如下四阶矩阵

取ϵ= 0.3，其伪谱Λϵ(A) ，定位集Dϵ(A)，Kϵ(A)，Bϵ(A)，(A)，Γϵ(A)分别如图1所示，中间区域表示由Grid-SVD法[9]计算给出的矩阵M伪谱Λϵ(A)，从内到外依次为伪谱定位集Dϵ(A)、Kϵ(A)、Bϵ(A)、(A)、Γϵ(A)的边界.显然，Dϵ(A) ⊆Bϵ(A) ⊆(A) ⊆Γϵ(A)，且Dϵ(A) ⊆Kϵ(A)⊆Γϵ(A).

本例表明新的伪谱定位集比文[16]，即定理1.1中的伪谱定位集小，且在某些情况下优于文[17]，即定理1.2和定理1.3中的伪谱定位集.

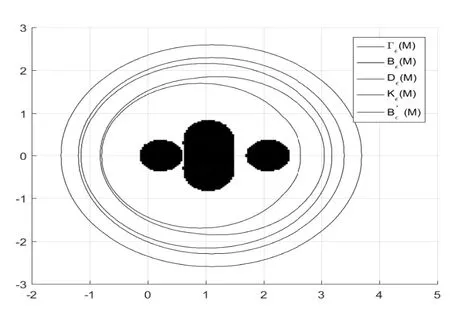
图1 矩阵M的伪谱定位集

3.应用

本节应用上述伪谱定位集对土壤生态系统的稳定性进行扰动分析.考虑土壤早期生态系统[17]，见图2，其中从上到下为该系统中的猎物到消费者，主要由八个功能类别的消费者组成：1.变形虫(顶级捕食者)，2.螨虫，3.真菌线虫，4.细菌性线虫，5.鞭毛虫，6.真菌，7.细菌，8.碎屑.应用文[20-21]的方法预处理得到群落矩阵A，其对角元素的绝对值表示相应功能组内的种内竞争(如配偶、空间、食物等)；对于i ＜j，-aij表示捕食者j对猎物i的捕食率；对于i ＞j，aij表示猎物i对捕食者j的供给率.考虑如下群落矩阵：

尽管矩阵特征值可用来分析土壤生态系统的稳定性，即如果该系统对应的群落矩阵的特征值都在复平面的左半平面，则该系统是稳定的，但在确定系统的生理参数和生物量密度时存在测量误差和经验不确定性，导致该群落矩阵并不能真实的反映实际情况，即该群落矩阵存在一定的扰动.此时应用矩阵特征值分析其稳定性并不有效，而应用伪谱来研究该系统的稳定性更加合理.另一方面，尽管可使用计算伪谱的算法，如Grid-SVD算法、Krylov子空间迭代算法、块隐式重启Arnoldi迭代算法等确定上述矩阵A的伪谱，进而对该系统的稳定性进行扰动分析，但却需要更多的计算.

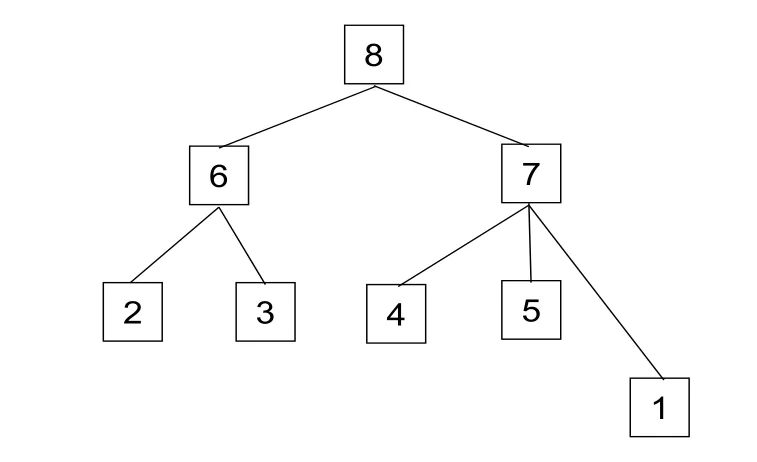
图2 4个营养层次的土壤食物网的营养相互作用

下面应用伪谱定位集分析上述土壤生态系统的稳定性.考虑扰动临界值ϵ= 1.25×10-2，对于任意的矩阵E满足‖E‖2≤ϵ，群落矩阵A的伪谱定位集Bϵ(A)位于左半复平面，见图3，即当矩阵A的扰动ϵ= 1.25×10-2时，A+E的特征值仍落在左半复平面，因此其对应的土壤生态系统仍然是稳定的.进一步，当扰动临界值ϵ= 1.75时，对于任意的矩阵E满足‖E‖2≤ϵ，群落矩阵A的伪谱定位集Dϵ(A)位于复平面的左半平面，见图4，即当矩阵A的扰动ϵ= 1.75时，A + E 的特征值仍落在左半复平面，因此其对应的土壤生态系统仍然是稳定的.然而当ϵ= 1.25×10-2或ϵ= 1.75时，文[16-17]所给的伪谱定位集与右半复平面的交非空，见图3和图4，因此无法得到上述结论.同时，可不必使用伪谱的算法计算群落矩阵A的伪谱，仍能判断在ϵ=1.25×10-2或ϵ=1.75扰动下对应的土壤生态系统仍然是稳定的.因此，避免了应用相关算法计算其伪谱，进而减少了计算量.

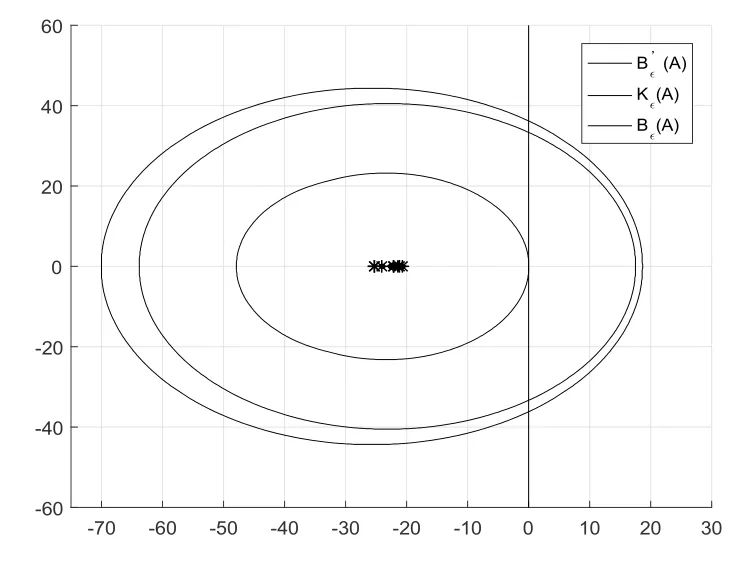
图3 当ϵ=1.25×10－2时，群落矩阵A的伪谱定位集Bϵ(A)

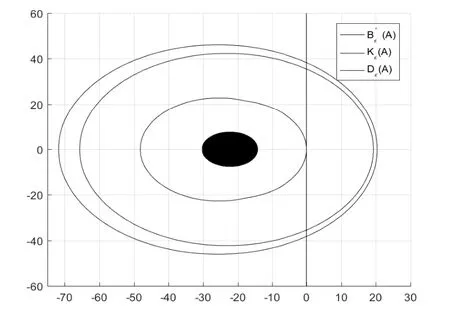
图4 当ϵ=1.75时，群落矩阵A的伪谱定位集Dϵ(A)