运用牛顿第二定律解决连接体问题

2022-03-24贵州省天柱民族中学胡朝平

中学生数理化(高中版.高考理化) 2022年9期

关键词：轻杆轻绳隔离法

■贵州省天柱民族中学胡朝平

多个相互关联的物体由轻绳、轻杆、轻弹簧等连接在一起,或者叠放在一起,构成的物体系统称为连接体。根据关联物体速度的关系和连接物体介质的不同特点,灵活选用整体法和隔离法,利用牛顿第二定律可以顺利求解相关问题。下面举例分析。

一、根据关联物体速度的关系可以分为同速连接体和关联速度连接体

1.同速连接体:相互关联的物体在拉力、弹力或摩擦力的作用下,具有相同的速度或相同的加速度。具体案例如图1所示。

2.关联速度连接体:相互关联的物体的速度和加速度大小相等,方向不同,但有所关联。具体案例如图2所示。

图2

二、根据连接物体介质的不同可以分为轻绳连接体、轻杆连接体、轻弹簧连接体或叠放连接体

1.轻绳连接体。

轻绳连接体的特点:轻绳中张力的方向只能沿着轻绳并指向轻绳收缩的方向,轻绳只能提供拉力,轻绳的张力可以发生突变;轻绳平动时,两端物体沿轻绳方向的速度(分速度)总相等;跨过滑轮、光滑杆、光滑钉子连接两端物体的若是同一根轻绳,则轻绳对两端物体的拉力大小相等。

例1质量不等的两个木块A、B,用跨过一轻质定滑轮的轻绳相连,在如图3所示的情况下,木块A、B一起做匀速运动。已知木块A、B与桌面之间的动摩擦因数均为μ,且μ＜1,重力加速度为g,空气阻力、滑轮摩擦均不计。若木块A、B的位置互相交换,则木块A的加速度为( )。

图3

A.(1-μ)g

B.(1-μ2)g

D.与木块A、B的质量有关

解析:木块A、B一起做匀速运动的过程中,根据牛顿第二定律得mAg=μmBg。木块A、B的位置互相交换后,同理得mBgμmAg=(mA+mB)a,解得a=(1-μ)g。

答案:A

2.轻杆连接体。

轻杆连接体的特点:轻杆对物体弹力的方向不一定沿着轻杆,轻杆既能提供压力,又能提供拉力,轻杆的弹力可以发生突变。若将轻杆固定在墙壁上,则轻杆不能转动。若用铰链将轻杆与墙壁相连,则轻杆的受力方向一定沿着轻杆的方向。轻杆平动时,连接体具有相同的平动速度;轻杆转动时,连接体具有相同的角速度,而线速度与转动半径成正比。一般情况下,连接体沿轻杆方向的分速度相等。

例2如图4所示,倾角θ=30°的斜面体固定在地面上,光滑斜面上放一辆小车。一根弹性杆的一端固定在小车上,另一端固定一个质量m=0.2 kg的小球,取重力加速度g=10 m/s2。求:

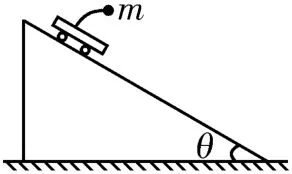
图4

(1)当在外力作用下小车静止在斜面上时,杆对小球的弹力。

(2)当小车由静止沿斜面下滑时,杆对小球的弹力。

解析:(1)当小车处于静止状态时,小球处于平衡状态,则杆对小球的弹力F=mg=2 N,方向竖直向上。

(2)当小球由静止沿斜面下滑时,由小车、杆和小球组成的整体的加速度a=,小球受到的合外力F合=ma=1 N,方向沿斜面向下。根据平行四边形定则可知,杆对小球的弹力F＇=,方向垂直于斜面向上。

3.轻弹簧连接体。

轻弹簧连接体的特点:弹簧可以产生和承受沿弹簧伸缩方向的拉力和压力。在弹簧发生形变的过程中,两端物体的速率不一定相等;在弹簧形变量最大时,两端物体的速率相等,两端物体受到弹簧的作用力大小相等。

例3如图5所示,置于粗糙水平面上的物块A和B用轻质弹簧连接,在水平恒力F的作用下,A、B两物块以相同的加速度向右运动。A、B两物块的质量关系为mA＞mB,两物块与水平面之间的动摩擦因数相同。为使弹簧稳定时的伸长量增大,下列操作可行的是( )。

图5

A.仅减小物块B的质量mB

B.仅增大物块A的质量mA

C.仅将物块A、B的位置对调

D.仅减小水平面的粗糙程度

解析:设弹簧的弹力为T,对由A、B两物块组成的整体应用牛顿第二定律得Fμ(mA+mB)g=(mA+mB)a,对物块B应用牛顿第二定律得T-μmBg=mBa,解得T=仅减小物块B的质量mB时,T减小,则弹簧稳定时的伸长量减小,选项A 错误;仅增大物块A的质量mA时,T减小,则弹簧稳定时的伸长量减小,选项B 错误;仅将物块A、B的位置对调,同理得弹簧的弹力,因mA＞mB,故T＇＞T,则弹簧稳定时的伸长量增大,选项C 正确;因为T与μ无关,所以仅减小水平面的粗糙程度,弹簧稳定时的伸长量不变,选项D错误。

答案:C

4.叠放连接体。

叠放连接体的特点:叠放在一起的物体之间由于相对运动或相对运动趋势会产生相互作用力;叠放在一起的物体之间相对静止时具有相同的速度和加速度;叠放在一起的物体之间相对运动时具有不相同的速度和不相同的加速度。

例4如图6所示,长木板放置在水平面上,一小物块置于长木板的中央,长木板和物块的质量均为m,物块与长木板之间的动摩擦因数为μ,长木板与水平面之间的动摩擦因数为,假设最大静摩擦力与滑动摩擦力大小相等,重力加速度为g。现对物块施加一水平向右的拉力F,则长木板加速度a的大小可能是( )。

图6

解析:水平面对长木板的最大静摩擦力,若拉力F≤fmax,则a=0,选项A 正确。若物块相对长木板运动,则μmg-·2mg=ma,解得此时的加速度为最大值,选项B 错误,C 正确。若长木板相对物块静止,长木板和物块一起做匀加速直线运动,则由物块和长木板组成的整体在水平方向上受到的力为Ffmax=2ma,解得,选项D 正确。

答案:ACD

处理连接体问题的方法:(1)若是同速连接体问题,则先用整体法求出F合与a的关系;若连接体内各物体具有相同的加速度,且不需要求物体之间的作用力,则可以把它们看成一个整体,分析整体受到的合力,应用牛顿第二定律求出加速度(或其他未知量),用隔离法求出F内与a的关系。(2)若是关联速度连接体问题,则先将两物体隔离开进行分析;若连接体内各物体的加速度不相同,或者需要求出连接体内各物体之间的作用力时,就需要用隔离法,应用牛顿第二定律列式求解。(3)整体法、隔离法往往需要交替运用。若连接体内各物体具有相同的加速度,且需要求出连接体内各物体之间的作用力时,可以先用整体法求出加速度,再选取合适的研究对象用隔离法,应用牛顿第二定律求作用力,即“先整体求加速度,再隔离求内力”。若已知连接体内物体之间的作用力,求连接体整体受到的外力,则“先隔离求加速度,再整体求外力”。

应用整体法和隔离法解题的技巧:(1)求解一起加速运动的物体系统问题时,若外力F作用在m1上,则m1和m2之间的相互作用力此结论与有无摩擦无关(若有摩擦,则两物体与接触面之间的动摩擦因数必须相同),物体系统沿水平面、斜面、竖直方向运动时,此结论都成立。两物体之间的连接物为轻弹簧、轻杆时,此结论也成立。(2)求解通过跨过滑轮的轻绳连接的物体系统问题时,若需要求出轻绳的拉力,则往往需要采用隔离法,因为通过跨过滑轮的轻绳连接的两物体的加速度虽然大小相同但方向不同。(3)求解叠加体系统临界问题可以按照如图7所示的程序进行。

图7

1.如图8所示,质量为m2的物块B放在光滑的水平桌面上,其上叠放质量为m1的物块A,用跨过光滑定滑轮的细线将物块A与质量为M的物块C相连,释放物块C,物块A和B一起以加速度大小a由静止开始运动。已知A、B两物块之间的动摩擦因数为μ,重力加速度大小为g,则细线中的弹力大小为( )。

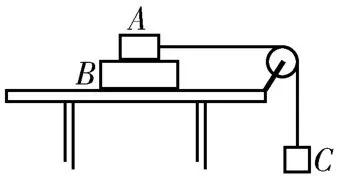
图8

A.Mg

B.M(g+a)

C.(m1+m2)a

D.m1a+μm1g

2.如图9甲所示,在粗糙的水平面上,质量分别为m和M的物块A、B用轻弹簧相连,两物块与水平面之间的动摩擦因数均为μ,当水平力F作用在物块B上,且两物块一起向右以加速度a1做匀加速运动时,弹簧的伸长量为x1;如图9乙所示,当将同样大小的恒力F沿着倾角为θ的光滑斜面方向作用在物块B上,且两物块一起以加速度a2沿斜面向上做匀加速运动时,弹簧的伸长量为x2。下列说法中正确的是( )。