万有引力与航天复习中应注意的速度反串
2022-03-24安徽省寿县一中
■安徽省寿县一中 王 银
■重庆市高新区教师进修学院 杨天才(特级教师,正高级教师)
模型1:太空升降机(太空舱模型)。
太空升降机是人类构想的一种通往太空的设备,它与普通电梯类似,利用太空升降机可以将乘客送入距离地球表面约3.6万千米的同步卫星中。
例1人类计划在未来建造太空升降机,即把长绳的一端搁置在地球的同步卫星上,另一端系住升降机,人坐在升降机里,科学家控制卫星上的电动机把升降机拉到卫星上去,放开绳子,升降机能到达地球上。已知地球表面的重力加速度g=10 m/s2,地球的半径R=6 400 km,地球的自转周期约为24 h。某航天员在地球表面用体重计称得体重为800 N,他站在升降机中,某时刻升降机以加速度a=10 m/s2垂直地面上升,此时再一次用同一体重计称得视重为850 N。忽略地球公转的影响,根据以上数据判断下列说法中正确的是( )。
A.若把绳子的一端搁置在同步卫星上,则可知绳子的长度至少有多长
B.可以求出升降机此时距地面的高度
C.可以求出升降机此时所受万有引力的大小
D.航天员在上升过程中绕地球做圆周运动的线速度逐渐增大
解析:因为同步卫星的离地高度是确定值,所以可知绳子的长度至少有多长,选项A正确。选航天员为研究对象,根据牛顿第二定律和黄金代换式的推论得N-mg'=ma,,解得选项B正确。因为不知道升降机的质量,所以不能求出升降机此时所受万有引力的大小,选项C 错误。航天员随升降机向上做加速度减小的加速运动,根据v=ω(R+h)可知,航天员在上升过程中绕地球做圆周运动的线速度逐渐增大,选项D 正确。
答案:ABD
点评:本题考查同学们通过阅读材料获取信息,建立物理模型的能力。因为绳中每点的角速度相同,且与地球的自转角速度相等,所以“航天员在上升过程中绕地球做圆周运动的线速度逐渐增大”是正确的。如果盲目利用“高轨低速大周期”的结论,就会得出错误答案。求解本题的关键是读懂新信息,构建新模型,做到“高起点,低落点”。
模型2:双星模型。
两颗质量可以相比的恒星围绕其连线上的某一点旋转,构成双星系统。双星系统中两颗恒星做匀速圆周运动所需的向心力由两颗恒星之间的万有引力提供,因为作用力与反作用力的大小相等,所以两颗恒星做圆周运动所需的向心力大小相等;因为两颗恒星绕其连线上的某一点做圆周运动,所以它们的运动周期是相等的,角速度也是相等的,线速度与两恒星的轨道半径成正比。
例2中国科学院云南天文台研究人员在对某密近双星进行观测和分析研究时,发现了一种双星轨道变化的新模式。该密近双星的周期突然变化,有可能是受到了来自其伴星的动力学扰动,从而引起了两子星间的物质交流。若小质量子星的物质被吸引而转移至大质量子星上(不考虑质量的损失),导致其周期增大为原来的k(k>1)倍,则下列说法中正确的是( )。
B.两子星间的万有引力增大
C.小质量子星的轨道半径增大
D.大质量子星的角速度增大
解析:该密近双星做圆周运动,万有引力提供向心力,设质量未转移时两子星的质量分别为m1、m2,且m1>m2,周期为T0,两子星的间距为R0,则又有r1+r2=R0,解得T0=因为T'=kT0,所以R'=,选项A 错误。质量未转移时两子星间的万有引力为,质量转移后两子星间的万有引力变为因为R'>R0,m2<m1,所以二者间的万有引力减小,选项B 错误。小质量子星质量未转移时的轨道半径,质量转移后的轨道半径因此,选项C 正确。根据可知,当周期T变大时,角速度ω变小,选项D 错误。
答案:C
点评:在双星模型中,因为两颗子星都在绕其连线上某点做匀速圆周运动,它们之间的距离始终不变,所以它们的运动周期是相等的,角速度也是相等的,线速度与两子星的轨道半径成正比。如果大星质量远大于小星质量,那么双星模型可等价于环绕模型,认为大星是静止的,小星围绕大星做匀速圆周运动,用环绕模型和双星模型计算的结果在误差范围内是相当的。
模型3:多星模型。
(1)特点:所研究星体所受万有引力的合力提供其做圆周运动所需的向心力,除中央星体外,各星体的角速度和周期相同。
(2)三星模型:三颗星体位于同一直线上,两颗质量均为m的环绕星围绕质量为M的中央星在同一半径为R的圆形轨道上运动,如图1甲所示;三颗质量均为m的星体位于等边三角形的三个顶点上,绕中心O做匀速圆周运动,如图1乙所示。
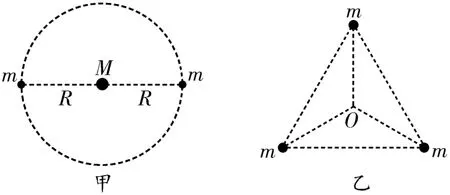
图1
(3)四星模型:四颗质量均为m的星体位于正方形的四个顶点上,沿着外接于正方形的圆形轨道做匀速圆周运动,如图2甲所示;三颗质量均为m的星体始终位于等边三角形的三个顶点上,另一颗质量为M的星体位于中心O,外围三颗星绕O点做匀速圆周运动,如图2乙所示。
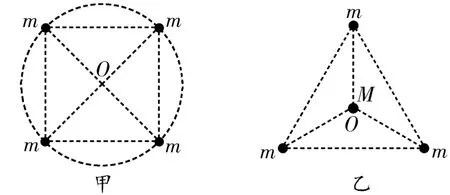
图2
例3天文观测中观测到有A、B、C三颗星位于边长为l的等边三角形的三个顶点上,并沿等边三角形的外接圆做周期为T的匀速圆周运动,如图3所示。已知引力常量为G,不计其他星体对它们的影响,关于这个三星系统,下列说法中正确的是( )。
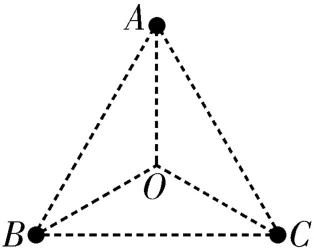
图3
A.三颗星的质量可能不相等
解析:在这个三星系统中,因为任意两颗星对第三颗星的合力指向圆心,所以这两颗星对第三颗星的万有引力等大;因为这两颗星到第三颗星的距离相同,所以这两颗星的质量相同,即三颗星的质量一定相同,选项A错误。设这三颗星的质量均为m,根据几何关系可知,这三颗星的轨道半径等于等边三角形外接圆的半径,则,解得,选项B 错误。任意两颗星之间的万有引力选项D 正确。这三颗星的线速度大小v=,选项C错误。
答案:D
点评:求解三星模型问题,与求解双星模型问题的方法一样,需要在找准三星模型与环绕模型差异的前提下,利用万有引力的合力提供向心力和角速度相等求解。
模型4:拉格朗日点模型。
1772年,法国数学家、力学家和天文学家拉格朗日在论文《三体问题》中指出:两个质量相差悬殊的天体(如太阳和地球)所在同一平面上有5个特殊点,如图4中的L1、L2、L3、L4、L5所示,人们称其为拉格朗日点。若飞行器位于这些点上,则在太阳与地球引力的共同作用下,可以几乎不消耗燃料而保持与地球同步绕太阳做圆周运动。
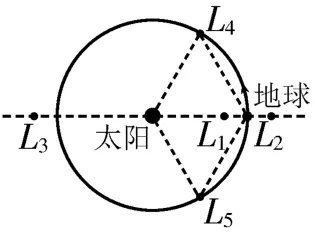
图4
例4如图5所示,拉格朗日点L1位于地球和月球连线上,处在该点的物体在地球和月球引力的共同作用下,可与月球一起以相同的周期绕地球运动。据此,科学家设想在拉格朗日点L1建立空间站,使其与月球同周期绕地球运动。以v1、T1、a1分别表示该空间站的线速度、周期、向心加速度的大小,以v2、T2、a2分别表示月球的线速度、周期、向心加速度的大小,以v3、T3、a3分别表示地球同步卫星的线速度、周期、向心加速度的大小。下列判断正确的是( )。

图5
A.v3>v2>v1B.T1>T2>T3
C.a3>a1>a2D.a3>a2>a1
解析:空间站与月球具有相同的周期与角速度,根据线速度v=ωr得v2>v1,同步卫星离地高度约为36 000 km,月球与地球之间的距离约为380 000 km,故同步卫星离地距离小于拉格朗日点L1离地距离,根据v=得v3>v2,选项A 正确。根据周期得T3<T1<T2,选项B 错误。在拉格朗日点L1建立空间站,使其与月球同周期绕地球运动,则位于拉格朗日点L1的空间站的轨道半径小于月球的轨道半径,根据向心加速度得a2>a1,同步卫星的轨道半径小于位于拉格朗日点L1的空间站的轨道半径,根据向心加速度得a3>a2>a1,选项C错误,D 正确。
答案:AD
点评:位于拉格朗日点的物体与月球同步运动(即同周期、同角速度),它在地球和月球二者万有引力的合力作用下做匀速圆周运动,与环绕模型存在本质上的区别。
总之,同学们要正确理解万有引力定律的物理含义,注意结论成立的条件,掌握相关模型的解题方法,实现思维的有效迁移。
