关于轻杆上的力方向的思考
2021-02-07余辉
余 辉
(乌鲁木齐八一中学 新疆 乌鲁木齐 830002)
1 轻杆上力的认识
高中物理中,在弹力这一节第一次认识轻杆模型,我们知道它不同于轻绳模型,它的力可以沿着杆向里,也可以沿着杆向外,也可以不沿杆. 所以一开始它就和轻绳同时出现,对比着学习来记忆.学生一开始学到这里会觉得杆模型难以理解,做题时不容易判断杆上力的方向.常见出题模型如下.
(1)图1中左侧为墙壁,轻绳一端固定在墙上,通过光滑定滑轮吊一个重物,轻杆左端固定在墙上,右端固定轻质定滑轮.
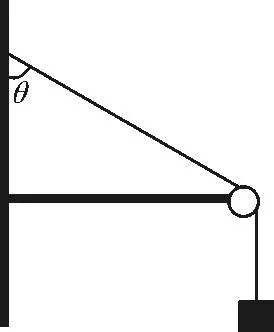
图1 常见出题模型一
(2)图2中左侧为墙壁,轻杆左端通过铰链拴接在墙上,右端分别与两根轻绳相连.

图2 常见出题模型二
两个图中物体质量均为m,轻绳与墙壁夹角均为θ=60°,重力加速度为g,求解轻杆对轻绳的弹力.
分析:图1中轻杆无法转动,所以轻杆右端受到的力可以沿着杆也可以不沿杆,又因为右端是光滑的滑轮,所以绳子拉力大小处处相等,对绳子上与滑轮接触点受力分析如图3所示,从而求得绳子拉力T大小为mg,方向向左上方与水平方向夹角为30°,由平衡条件,轻杆上的滑轮对轻绳的弹力F大小为mg,向右上方,与水平方向夹角为30°.
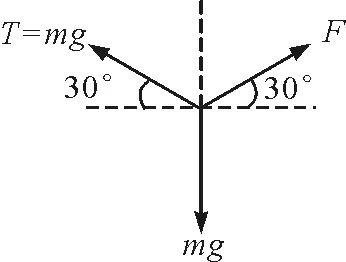
图3 图1中绳子上与滑轮接触点受力分析
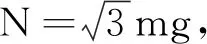
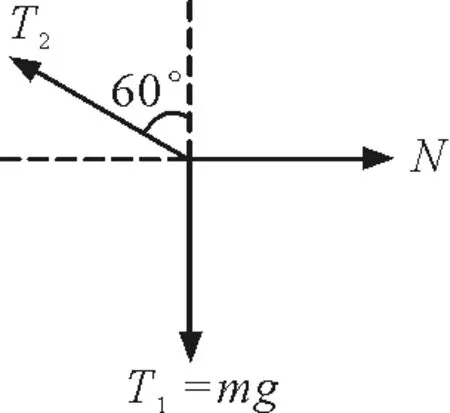
图4 图2中轻绳上与轻杆右端接触点受力分析
这是关于轻杆的非常经典的习题,轻杆上的力是否沿杆是一个难点.正因为这个难点,在后面的圆周运动的学习中会碰到类似的难点问题.
2 圆周运动中轻杆模型的疑惑
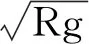
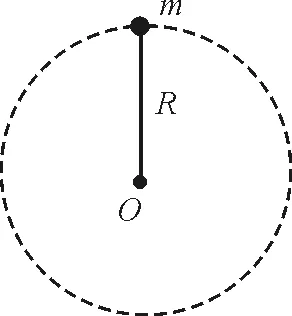
图5 竖直平面内圆周运动模型
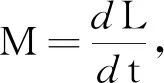
图5中,以圆心为转轴,在最高点时轻杆与小球系统受到重力过圆心,所以力矩M为零,系统转动惯量I=mR2(忽略轻杆质量)不为零,则根据公式M=Iβ知β=0,再根据公式at=Rβ可知切向加速度为零,则最高点时切向没有加速度,也就没有力的作用,轻杆给小球的力一定沿着杆.这样就解决了我们之前的疑惑.
3 拓展
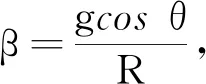

图6 问题拓展示意图一
进一步拓展,在机械能守恒中我们常常会碰到如图7所示模型,轻杆两边分别连接质量为m和2m的小球,轻杆可以绕位于圆心的轴无摩擦的转动,圆半径为R,初速度为零释放,在最低点时轻杆对质量为m的小球弹力为多大?这个问题求解并不难,我们只需要利用机械能守恒解出m运动到最高点时的速度,再利用向心力公式就可以求出弹力,这里我们也是默认最高点时轻杆给小球m的弹力是沿着杆的.但是在m向上运动过程中,轻杆给小球的力并不沿着杆,因为小球m动能增加,重力又对它做负功,则轻杆对小球m必然做正功,轻杆给的力不可能始终垂直于速度,也就是不能始终沿着杆.
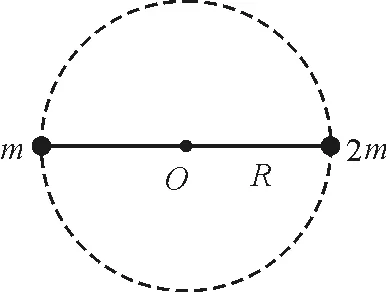
图7 问题拓展示意图二
既然之前轻杆对小球做正功了,为什么在最高点时就默认轻杆对小球的力就沿着杆了呢?这里我们也需要利用角动量定理来解释,当m球转到最高点时2m球在最低点,以圆心为轴这个整体受到外力都经过圆心,所以力矩M为零,则角加速度β=0,切向加速度at=0,则轻杆给小球的力一定沿着杆方向.
由此,我们通过竞赛中常用的角动量定理解释了我们在轻杆模型中这几点疑惑.在教学中我们经常会碰到一些考试中不太会考到的问题,考试中几乎不出现导致我们也并不重视,但是这些问题的确是存在的,学生会问,我们自己也会很疑惑.这时候就需要学习一些新的知识来帮我们彻底解决.这样我们脑海中的知识体系才能完整.
