(D3(4),λ)-支架和(D3(4),λ)-可分解的可分组设计的存在谱

杨 青, 郑 义

(1.淮阴师范学院 数学与统计学院, 江苏 淮安 223300; 2.南京师范大学 数学科学学院, 江苏 南京 210023)

0 引言及预备知识

V(H)和E(H)分别表示图H的顶点集和边集,λH表示重数为λ的多重图,K(m1,m2,…,mu)表示有u个部(组)的完全多部图,Ku表示有u个顶点的完全图.

设G是一些图的集合,图H的一个G-分解是指将E(H)划分为H的一些同构于G中的子图(称为区组).图H的部分顶点不交且划分V(H)的子图称为一个平行类.若平行类中的区组都同构于某一个图,则称该平行类是一致的.若图H存在一个G-分解,且所有区组可以被划分为若干个平行类,则称图H存在一个可分解的G-分解.关于完全图的G-分解有着广泛研究[1-4].

图λK(m1,m2,…,mu)的一个(可分解的)G-分解称为(可分解的)可分组设计,记作(G’,λ)-(R)GDD.当λ=1时,记号中λ可以省略,简记为G-(R)GDD;当G’中只有一个图G时,将(G’,λ)-(R)GDD简记为(G,λ)-(R)GDD.(G’,λ)-(R)GDD的型是指完全多部图中部大小的多重集,通常用1i2j3k…来表示,即有i个大小为1的部,j个大小为2的部,等等.

图H的部分顶点不交且顶点集的并真包含于V(H)的子图,称为一个带洞平行类.若型为gu的(G’,λ)-GDD的区组集可以被划分为若干个带洞平行类,每个带洞平行类的点集都恰好缺少一个组上的点,则称该GDD是一个支架.支架设计在图分解中起着关键性作用,关于组型一致支架的讨论已经有许多.如Colbourn 等人研究了(K2,λ)-支架的存在性[5];Chen F和Cao H完全解决了(K1,3,λ)-支架的存在谱[6];Cao等人着手研究了(Ck,1)-支架的存在性[7];Buratti等人完全解决了(CK,λ)-支架的存在谱[8];Stinson解决了(k3,1)-支架的存在谱[9];其他关于(k4,λ)-支架的研究也比较多[10-14].

本文主要研究G为D3(4)的支架和可分解的可分组设计的存在性问题,其中D3(4)为完全图K4去掉一个一因子,即点集为{a,b,c,d}的完全图去掉边{a,d}和{b,d}后得到的图.为方便起见,以下用(a,b,c,d)表示D3(4).当然,也有其他关于此类图的标记[15-16].

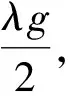
引理1 若型为gu的(D3(4),λ))-支架存在,则

λg≡0(mod 2),g(u-1)≡0(mod 4),u≥4, 且当u=4时,g≡0(mod 4).

引理2[17]型为gu的D3(4)-支架存在,当且仅当

u≥4,g(u-1)≡0(mod 4),g≡0(mod 2).

引理3 若型为gu的(D3(4),λ))-RGDD存在,则

λg(u-1)≡0(mod 2),gu≡0(mod 4),u≥3, 且当u=3时,g≡0(mod 4).

引理4[18]型为gu的D3(4)-RGDD存在,当且仅当

u≥3,g(u-1)≡0(mod 2),g≡0(mod 4).

下面将对任意相遇数λ,解决(D3(4),λ)-支架与(D3(4),λ)-RGDD这两类设计的存在性.

1 (D3(4),λ)-支架的存在谱

设K是一个正整数集,若G’={K1,K2,…,Kt},其中|V(Ki)|∈K(1≤i≤t),则将G’-GDD记为K-GDD,型为1v的K-GDD称为成对平衡设计,记作(K,v)-PBD.当K={k}时,简记为k-GDD.

接下来,将用到以下递推构造方法,类似的证明过程[9,19]略.首先,介绍一个定义.给定一个图G,字典积G[n]的点集是

{xi|x∈V(G),i∈Zn}, 且{xi,yi}∈E(G[n]),i,j∈Zn当且仅当{x,y}∈E(G).

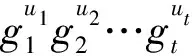
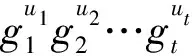
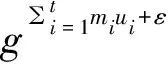
引理5 对任意m≥1且m≠2,6,存在图D3(4)[m]的D3(4)-分解.

证明由(K3,1)-RGDD(m3)可得其存在性[5].设其组为{x}×Zn,x∈{a,b,c}.将其m个平行类标记为

由文[5]知,K3[m]有1-因子分解,设其组为{y}×Zn,y∈{c,d},1-因子为

设图D3(4)[m]的点集为{a,b,c,d}×Zn,

令

容易验证R1,R2,…,Rm即为所需的分解.

接下来，解决(D3(4),λ)-支架的存在性问题.由引理1可知，只需解决λ=1和λ=2的情形.前者已经由引理2解决,下面解决λ=2的情形.

引理6 对任意u≥5且u≡1(mod) 4,存在型为1u的(D3(4),2)-支架.

证明对u∈{5,9,13},设顶点集为Zu,组为Mi={i},i∈Zu.缺掉组Mi的带洞平行类是{P+i},其中P中的区组如下.

u=5,P:{2,3,1,4},

u=9,P:{2,4,1,5},{3,7,6,8},

u=13,P:{2,3,1,5},{7,10,4,9},{8,12,6,11}.

对任意u≥17,存在一个型为4(u-1)/4的D3(4)-支架[17],将每个区组重复一次可得一个型为4(u-1)/4的(D3(4),2)-支架.运用构造3,其中当ε=1时,可得型为1u的(D3(4),2)-支架,其中的输入设计型为15的(D3(4),2)-支架在证明中已经构造.

定理1 型为gu的(D3(4),λ)-支架存在,当且仅当

λg≡0(mod 2),g(u-1)≡0(mod 4),u≥4.

证明分两种情形:

情形1:λ≡1(mod 2),λ=1的情形见引理2,将λ=2其每个区组重复λ次得到型为gu的(D3(4),2)-支架.

情形2:λ≡0(mod 2).分以下3种情况考虑λ=2:

1)g≡1(mod 2),且u≡1(mod 4),u≥5.

由引理5知,D3(4)[g]有D3(4)-分解.由引理6知,存在型为1u的(D3(4),2)-支架.取m=g并运用构造1可得型为gu的((D3(4),2)-支架.

2)g≡2(mod 4),且u≡1(mod 2),u≥5.

由引理2知,存在型为gu的D3(4)-支架.将其每个区组重复两次即可得型为gu的(D3(4),2)-支架.

3)g≡0(mod 4),且u≥4.

由引理2知,存在型为gu的D3(4)-支架.将其每个区组重复两次即可得型为gu的(D3(4),2)-支架.

2 (D3(4),λ)-RGDD的存在谱

首先，给出一些(D3(4),λ)-RGDD的递推方法.

构造4[1,6,19]若存在型为gu的(G,λ)-RGDD,且G[m]有G-因子分解,则存在型为(mg)u的(G,λ)-RGDD.

构造5[1,6,19]若同时存在型为(gu)l和gu的(G,λ)-RGDD,则存在型为gul的(G,λ)-RGDD.

对(D3(4),λ)-RGDD(gu)的存在性,由引理3可知，仅需考虑λ=1和λ=2的情况.前者已由引理4解决.下面解决λ=2.

引理7 存在一个型为4u的(D3(4),2)-RGDD,其中u≥3.

证明由引理4可知存在D3(4)-RGDD,将其区组重复一次可得所求设计.

引理8 对任意u≥4且u≡0(mod 2),存在型为2u的(D3(4),2)-RGDD.

证明由引理4可知存在D3(4)-RGDD,将其区组重复一次可得所求设计.

引理9 对任意u≥4且u≡0(mod 4),存在型为1u的(D3(4),2)-RGDD.

证明对u=4，8,设点集为Zu-1∪{∞0},组为{i},i∈Zu-1和{∞0}.所需的u-1个平行类可以从一个已知的平行类P通过+1(modu-1)生成.P中的区组如下:

u=4,P：{0,1,2,∞0},

u=8,P：{4,0,1,2},{5,3,6,∞0}.

定理2 型为gu的(D3(4),λ)-RGDD存在,当且仅当

λg(u-1)≡0(mod 2),gu≡0(mod 4),u≥3.

证明下面分两种情形证明.

情形1:λ≡1(mod 2).由引理4可知,存在(D3(4),1)-RGDD(gu),将其区组重复λ次即得(D3(4),λ)-RGDD(gu).

1)g≡1(mod 2).此时u≡0(mod 4),u≥4,令m=g,运用构造4,利用引理9中的输入设计型为1u的(D3(4),2)-RGDD,可得型为gu的(D3(4),λ)-RGDD.

2)g≡2(mod 4).此时u≡0(mod 2),u≥4.由引理4可知,存在(D3(4),1)-RGDD(gu),将其区组重复2次即得(D3(4),2)-RGDD(gu).

3)g≡0(mod 4).此时u≥3.由引理4可知,存在(D3(4),1)-RGDD(gu),将其区组重复2次即得(D3(4),2)-RGDD(gu).

3 总结

本文对任意相遇数λ,研究了图D3(4)的两类设计的存在性.主要结果如下:

1) 型为gu的(D3(4),λ)-支架存在的充要条件为λg≡0(mod 2),g(u-1)≡0(mod 4),u≥4,且当u=4时,g≡0(mod 4);

2) 型为gu的(D3(4),λ)-RGDD存在的充要条件为λg(u-1)≡0(mod 2),gu≡0(mod 4),u≥3,且当u=3时,g≡0(mod 4).