交互对话培养小学生的发散思维

文|徐素珍 郑卫红

一、营造“情境场”，参与中与学习对象对话

自主探索、动手实践、合作交流是现代小学生主要的学习方式。因此，我们要在数学课堂中创设一个便于学生动手实践的“情境场”，通过观察、动手实践、思考分析、逻辑推理等数学活动，让学生在数学活动中加深对数学知识的理解。将抽象的数学问题放到具体的生活情境中，让学生边操作、边思考、边推理、边得出实验结论，提高课堂教学的有效性，培养学生的发散思维能力。

【案例1】人教版四年级下册第111 页有一道关于汉诺塔的思考题，移动的规则是每次只能移动1 颗珠子，大珠子不能放在小珠子的上面，我将这道思考题进行改编，提出了层层递进的数学问题，如果是4 个圆盘、5 个圆盘或64个圆盘呢，各要移动多少次？

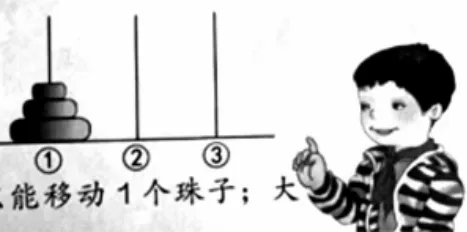
师：同学们，我们化繁为简，先来研究移动一个圆盘或两个圆盘要移动多少次？

生：将一个圆盘从1 号杆移动到2 号杆移动一次就可以了。将两个圆盘从1 号杆移动到3 号杆需要移动3 次，先将小珠子移到2 号杆，接着将大珠子移到3号杆，然后再将2 号杆上的小珠子移到三号杆上。

师：那么移动3 个圆盘和4个圆盘呢？

生：移动3 个圆盘一共要移动7 次。

生：老师，4 个圆盘的移动好复杂，移着移着就忘记几次了，有没有规律呀？

师：我们已经研究过移动3个圆盘需要7 次，可以借助移动3个圆盘的结果进行递推。

生：老师，我知道了，1 号杆上面3 个圆盘借助其他杆移动到2号杆需要7 次，再将1 号杆的最大圆盘移到3 号杆需要1 次，最后将2 号杆上的3 个圆盘移动到3 号杆又需要7 次，所以是7+1+7=15。

生：移动5 个圆盘移动的次数是15+1+15=31。

生：老师，我找到规律了，移动一个圆盘是21-1 次，移动2 个圆盘是22-1 次，移动3 个圆盘23-1 次……移动64 个圆盘就是264-1 次。

师：那么移动n 个圆盘最少需要多少次呢？

生：移动n 个圆盘的最少需要2n-1 次？

通过探究移动1 个、2 个和3个圆盘最少需要多少次的问题时，学生丝毫没有感受到难，但是在解决移动4 个圆盘最少需要多少次这个问题时，学生疑惑的眼神告诉我，这个问题好难。此时，教师引导学生能不能借助前面移动3 个圆盘的体验来递推移动4个圆盘最少需要多少次的问题呢？学生恍然大悟，借助移动3 个圆盘的经验来递推移动4 个圆盘的最少次数，最后得出移动n 个圆盘的最少次数是2n-1。学生在“情境场”中操作、感悟、分析、递推等过程中，培养了发散思维，收获了成功的快乐。

二、营造“互动场”，协同中与学习同伴对话

数学课堂中营造一个氛围平等的能够促进学生和学习同伴展开协同学习的“互动场”（“学习圈”），让学生在自主表征、表达倾听、质疑反思等学习过程中不断建构、解构和重构，学生的发散思维得到很好的培养。

【案例2】8 瓶酸奶和3 瓶纯奶共重3000 克，3 瓶酸奶和8 瓶纯奶共重2500 克，每瓶酸奶和每瓶纯奶各重多少克？

师：请每个同学独立思考5分钟，然后在“学习圈”内交流、探讨，再展示、分享不同的解法。

师：对于这道题目，大家讨论后有什么样的方法呢？

生：我们组是把8 瓶酸奶和3瓶纯奶共重3000 克利用等式的性质转变成24 瓶酸奶和9 瓶纯奶共重9000 克，把3 瓶酸奶和8瓶纯奶共重2500 克转变成24 瓶酸奶和64 瓶纯奶共重20000 克，然后用（20000-9000）÷（64-9）求出纯奶的重量。

生：也可以利用等式的性质把纯奶变成一样再求解。

师：还有不同的想法吗？请你们“学习圈”内成员继续交流一下。

生：我们组的想法跟他们不一样。我们是用（3000-2500）÷5 求出一瓶酸奶比一瓶纯奶多100克，再用（3000-8×100）÷11 求出1瓶纯奶的重量。

生：用（3000-2500）÷5 求出一瓶酸奶比一瓶纯奶多100 克，再用（2500+8×100）÷11 求出1 瓶酸奶的重量。

课始阶段，有部分学生的思路打不开，这个问题没办法解决，正是通过组员的分享、碰撞和讨论，学生才想出了一种又一种的方法，学生在这样的“互动场”中进行深度学习和深度对话，他们的视野得以打开，灵感得以激发，思维得以发散，从而创造性地想出了多种解决问题的方法。

三、营造“思维场”，共创中与自我深度对话

每一位学生的元认知水平不同，所处的环境不同，使得每一位学生的思维水平也是各异的，不同的学生对某一个问题的思考过程也是迥异的。在数学课堂中如果能够构建一个共同进步、共同成长的“思维场”，学生在“思维场”中，通过表征，表达自己的想法；通过倾听，理解不同的思路，对自己的想法进行修正；通过回顾反思，内化自己的思考，达成共识。

【案例3】把长84 厘米的铁丝围成一个长方形，使长比宽多6厘米，长和宽各是多少厘米？

师：请你们先画出线段图，然后独立思考，把想法写下来，接着与同桌同学进行交流，最后进行分享。

生：84÷2=42，42-6=36，36÷2=18 就是宽的长度，18+6=24 就是长的数量。

生：84÷2=42，42+6=48，48÷2=24 求出长，用24-6=18 求出宽。

师：请四人小组观察线段图再讨论一下，还有没有别的解法？

生：84-（6+6）=72，用72÷4=18 求出宽，用18+6=24 求出长。

生：84+（6+6）=96，用96÷4=24 求出长，用24-6=18 求出宽。

师：想想还有没有不同的方法？

生：用84÷4=21 求出宽与3厘米之和，21-3=18 求出宽，18+6=24，求出长。

上述案例，首先是请学生独立思考，将自己的想法自主表征出来，接着请同桌同学展开讨论，通过思维碰撞，激活了学生的学习潜力，然后教师请学生继续思考，学生对原来所画的线段图稍作改编，从而想出了一种与众不同的方法，即用84 除以4 求出宽与3 厘米之和，再求出长方形的长和宽。这道题目的教学，教师运用了数形结合思想，学生通过不同的图式找到解决问题的不同方法，学生的思维不断地发散、不断地进阶，学习水平不断地提升。

在小学数学课堂教学中，教师创设利于学生深度学习的“情境场”“互动场”和“思维场”至关重要。创设情境场，学生通过观察、实践、思考、探索等数学活动，自己悟出数学知识的真谛，体会探索知识的方法，享受探索成功的喜悦；创设互动场，学生在合作交流中充分展示思考的学习成果，满足学生的表现欲望，实现学生之间优势的互补，培养学生的团结协作能力；创设思维场，在知识关键处给学生安排足够的思考时间，不但能使学生拥有充分的从事数学活动的机会，而且留给学生思维驰骋的空间，让发散思维能力的培养落到实处。