近岛礁八模块超大型浮体水动力载荷研究

丁 军，杨伟楠，王思雨，谢卓雨，耿彦超，刘小龙，徐胜文

(1.中国船舶科学研究中心，江苏 无锡 214082；2.上海交通大学船舶海洋与建筑工程学院，上海 200240)

0 引 言

所谓超大型浮体（Very Large Floating Structure，VLFS），主要是指那些尺度以公里计的浮式海洋结构物，如海上机场、大型海上基地、跨海浮式大桥、旅游综合体等，甚至是一些工业基地、应急基地、再生公园和海上城市等。与传统在礁滩上填土打桩建大型海、空港基地相比，超大型浮体存在以下五大优势[1]：（1）避免建筑材料与施工机械的长距离输运及长期后勤保障；（2）现场施工周期短，可在较短时间内完成首期配置的就位及基本功能的启用；（3）可根据现场需求，增减规模与更改功能或驻地，适应瞬息万变的国际形势；（4）结构设施可以免于地震等自然灾害的损坏；（5）对生态环境的影响较小，不淤塞水港，也不破坏洋流。

超大型浮体概念的提出最早可追溯到1895年法国儒勒⋅凡尔纳所著的科幻小说中描述的大型浮岛。经过一个多世纪的研究，目前国内外开展过的研究主要涉及布置在深远海或遮蔽港口内的超大型浮体动响应预报问题，分别形成了浮箱型和半潜式两种主要方案。其中以日本方案为代表的浮箱方案侧重于民航使用[2]，主要解决陆地面积不足和地震频发的问题，分四个阶段逐步进行研发，建造完成了一个千米长由多个模块焊接而成的演示结构，并进行了飞机起降的安全性试验。美国方案号称“移动式离岸基地MOB”[3]，采用半潜式结构模块，单个模块长度300 m、宽140 m，排水量近几十万吨。虽然该研究项目已经完成，但目前还没有正式建造的报道。

国内吴有生院士在上世纪80年代初开创性地提出了三维水弹性力学理论，为超大型浮体的水弹性评估提供了有力的分析工具[4-5]。本世纪初上海交通大学得到了国家自然科学重点项目的资助，完成了开阔海域中箱型超大型浮体的探索性研究[6]。近年来，在国家科技部和工信部支持下，以中国船舶科学研究中心为牵头单位，联合了国内多所高校、研究所和企业单位针对复杂岛礁环境条件下超大型浮体（见图1）开展了系列研究，形成了一批重要的研究成果，进一步推动了超大型浮体由基础研究到应用开发的转变进程[7-10]。

图1 近岛礁多模块超大型浮体示意图Fig.1 Sketch of multi-module VLFS deployed near islands and reefs

由于超大型浮体刚度较小，其自身的弹性变形与在波浪中的刚体运动响应可能处在一个量级，因此传统理论中的刚性假定具有一定的局限性，水弹性理论的应用显得尤为重要。经过一个多世纪的研究，目前国内外开展过的研究主要涉及布置在深远海或遮蔽港口内的超大型浮体动响应预报问题，但仍然存在针对复杂恶劣海洋环境条件下结构载荷及安全性的重大基础问题尚待深入研究，特别是在近岸或岛礁资源开发利用时，超大型浮体将面临更加复杂的波浪环境条件[11-15]，如何在近岸或岛礁附近合理地布置尺度达千米级的超大型浮体是首先要面临的重要问题，这需要综合考虑许多因素，如超大型浮体自身的动响应大小、对周围环境的影响、功能性的便捷实现、经济合理性等。本文以超大型浮体动响应作为切入点，基于复杂环境中浮体水弹性响应直接耦合分析方法，开展八模块超大型浮体相对某典型岛礁不同布置方案时其运动和连接器载荷响应结果对比分析，掌握八模块超大型浮体动响应规律，从而为近岛礁八模块超大型浮体总体布置提供参考依据。

1 基本理论

当一个大型浮体布置在近岸或岛礁附近的海域时，复杂海底地形和非均匀波浪条件等因素的影响将不可忽略，经典三维水弹性力学理论中仅能考虑深水或有限均匀水深Green函数的势流模式将不再适用。文中将基于水波局域模型——Boussinesq 方程和Rankine 源方法，建立包含复杂海底地形和时空分布不均匀波浪环境中的超大型浮体水弹性响应直接耦合求解方法。该方法中将引入一个虚拟控制面，从而将整个计算流场划分为内域和外域，外域采用Boussinesq方程模拟波浪在复杂海底地形上的传播变形，内域采用Rankine源方法考虑波浪、浮体与复杂海底地形的相互作用（见图2 和表1）。在虚拟控制面上，流速分布和波面升高作为连续条件从而将内外域流场耦合起来。

图2 直接耦合分析方法计算域Fig.2 Computational domain for the direct coupling method

表1 相关参数说明Tab.1 Notations of the parameters

1.1 外域-Boussinesq方程

采用完全非线性Boussinesq方程[16]对外域中波浪传播变形进行模拟，该方程在近海波浪传播变形的研究中得到了广泛的应用，可综合反映波浪的非线性与色散性。其控制方程（包括质量守恒方程与动量守恒方程）形式如下：

质量守恒方程为

式中，vα=(uα,vα)为z=zα= -0.531h处的水平质点速度,η为波高，h为水深，vαt中的下标t代表对时间的导数。

1.2 内域-Rankine源方法及三维时域水弹性分析

浮体结构振动位移可用模态叠加法表示为

1.3 内外域匹配面条件

（2）在虚拟控制面SC上获得内域绕射与辐射波速度势ϕD，ψ1k与χk（k=1，2，…）的边界条件：假定绕射波与辐射波（这里统一定义为扰动波，对应扰动速度势ϕd）可以完全穿过控制面SC。在外域海底与礁盘上的反射和衰减效应会通过外域Boussinesq 方程的求解，从而体现在本时间步tn的后面迭代结果中。同时，为了消除它的反射效应，在SC外一定距离处设一个虚拟消波面S′C来吸收扰动波。本文采用目前常用的人工消波方法[17]，在自由面动力学条件中加入耗散项，则自由面条件可进一步表示为

2 研究对象

本文的研究对象为布置在近岛礁海域的八模块超大型浮体，水动力参数见表2，单模块长300.0 m，宽100.0 m，高27.0 m，排水量为93 614.0 t，模块间通过对称布置的2个长6 m连接器进行组合，距中纵剖面28 m。连接器距基线25 m，位于模块上体甲板处。铰接构型连接器释放了模块间相对纵摇运动，各方向的刚度分别为Kx=8.77E+10 N/m，Ky=8.77E+12 N/m，Kz=8.77E+10 N/m，Rx=3.36E+10 N⋅m/rad，Rz=6.24E+12 N⋅m/rad，Ry=0。

表2 八模块超大型浮体水动力参数Tab.2 Hydrodynamic parameters of 8-module VLFS

超大型浮体拟布置在一个长1600 m、宽700 m 的岛礁之后，岛礁露出水面部分的尺度为400 m×150 m，图3 给出了超大型浮体轴线与远场入射波方向成90°夹角时的总平面布置图，图中M1～M8代表超大型浮体八个模块编号，C1～C14代表14个连接器编号。在上海交通大学海洋工程国家重点试验室海洋深水试验池对该布置工况下的超大型浮体开展了水池模型试验研究（模型缩尺比λ=1:100，见图4）[18]，获得了不同海况条件下浮体运动、连接器载荷等参数的响应规律，可为相关数值方法预报结果的对比分析提供参考依据。

图3 超大型浮体总平面布置图Fig.3 General layout of VLFS

图4 近岛礁八模块浮体水池模型试验Fig.4 Model tests of 8-module VLFS near an island

同时，为进一步分析不同布置方案对超大型浮体动响应的影响，在数值预报中将调整超大型浮体轴线与远场入射波的夹角，如图5所示，分别给出了夹角为0°、45°和80°的三种总平面布置示意图。

图5 超大型浮体相对岛礁的不同布置方案Fig.5 Different layout schemes of VLFS relative to islands and reefs

3 不同布置方案超大型浮体动响应结果对比分析

3.1 波浪场演化

图6 给出了H=3.0 m，T=13.0 s 规则波工况下四种不同布置方案计算域内的波面图。结果表明四种布置方案下岛礁模型前侧的波浪基本相同，但后侧由于超大型浮体自身的绕射波和辐射波的影响，使得波面演化情况出现了非常大的差异，同时超大型浮体不同位置处的波浪也存在非常明显的非均匀性。

图6 不同布置方案非均匀波浪场预报结果（远场入射波：H=3.0 m，T=13.0 s）Fig.6 Inhomogeneous wave field of different layout schemes(Incident wave:H=3.0 m，T=13.0 s)

3.2 运动响应

图7给出了相对远场入射波方向呈不同浪向角布置方案中模块1的运动响应结果。为对比分析，图中同样给出了相对远场入射波夹角为90°布置工况下的模型试验结果，可以发现：

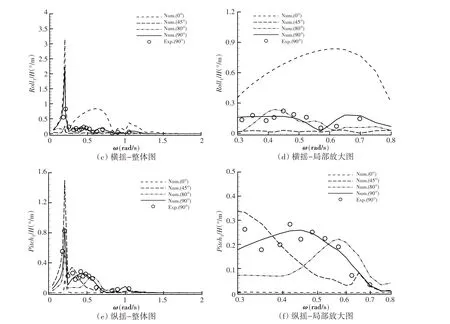
图7 不同布置方案超大型浮体模块1运动响应RAO结果Fig.7 Motion RAOs of Module 1 for different layout schemes

（1）对于相对远场入射波夹角为90°布置工况，运动响应数值预报结果与模型试验结果吻合良好，说明了本文建立的理论方法具有较高的精度；

（2）不同布置方案中浮体运动响应差异性十分显著，结合图6 中的波面变化图可以发现，由于岛礁对波浪传播的遮蔽和绕射作用，使得超大型浮体上实际遭遇的浪向发生了明显的偏转，例如对于浮体的横摇运动，一般情况下，其最大值应该发生在横浪向时，但却发生在0°布置角方案，而对于纵摇，在无岛礁遮挡的情况下，应该在0°布置角工况较大，但该布置位置的结果却几乎为零；

（3）究其原因，主要是在0°布置角方案时，由于岛礁的作用，超大型浮体的遭遇浪向却几乎改变为90°，而90°布置角方案时则相反，从而导致考虑岛礁产生的非均匀波浪影响后，超大型浮体的运动响应结果出现了明显异于传统无岛礁影响时均匀波浪作用下浮体的响应规律。

3.3 连接器载荷响应

图8 给出了不同布置方案工况下C1和C7 连接器载荷RAO 的数值预报结果及相对远场入射波夹角为90°布置工况下的模型试验结果。可以发现：

图8 不同布置方案下C1和C7连接器载荷响应RAO结果Fig.8 Connector load RAOs of C1 and C7 for different layout schemes

（1）针对连接器载荷响应，数值预报结果同样与模型试验结果吻合良好，进一步验证了数值模拟方法的可靠性；

（2）总体来说，80°和90°两个布置角方案中的连接器载荷明显较大，而0°布置角方案中连接器的载荷几乎为零，与上节中运动响应规律的产生原因相同，由于岛礁对波浪演化的遮蔽和绕射作用，使得远场入射波传播至0°布置角的超大型浮体周围时正好变成了相对于轴线为90°的浮体遭遇波浪，从而导致连接器的载荷响应非常小。

以短期海况（H1/3=5.54 m，Tp=10.7 s）作为输入，开展连接器载荷的短期响应预报（见表3），结果表明，连接器载荷响应的最大值都发生在90º布置角的方案下，其中C7 连接器Fx方向的载荷接近八万吨，而Fy和Fz方向的载荷相对较小，都在千吨量级。

表3 不同布置方案下连接器载荷响应短期预报值（单位：t，H1/3=5.54 m，Tp=10.7 s）Tab.3 Short term prediction values of connector loads for different layout schemes

根据超大型浮体可能布置海域的实测海浪统计资料（见表4），对连接器载荷响应进行长期预报。图9 给出了C1 和C7 连接器载荷响应长期预报结果，结果表明，连接器载荷水平与负对数超越概率之间基本呈线性关系。表5 中列出了当-lgP等于2、4、6、8 和10 时对应的长期预报结果，当取超大型浮体一生中遭遇的波浪载荷循环数n=108，即对应概率水平-lgP=8 时，发现连接器载荷长期响应结果同样是处在中间位置的C7连接器在Fx方向的载荷最大，达到了八万吨；而Fy和Fz方向的载荷相对较小，在千吨量级。

表4 超大型浮体可能布置岛礁海域的海浪实测统计资料Tab.4 Measured statistical wave data where VLFS may be arranged

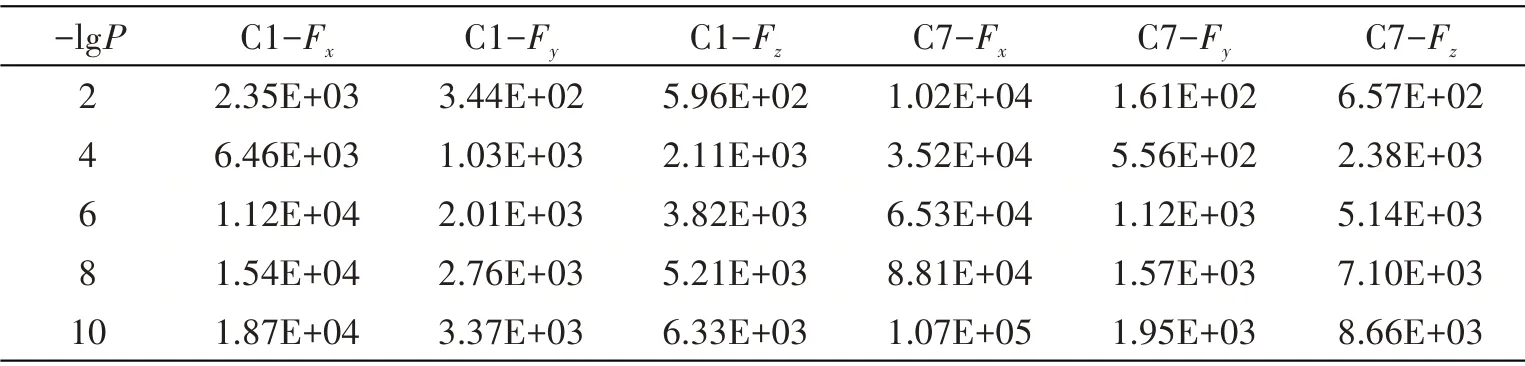
表5 不同概率水平下连接器载荷预报结果（单位：t）Tab.5 Numerical results of the connector load under different probability levels

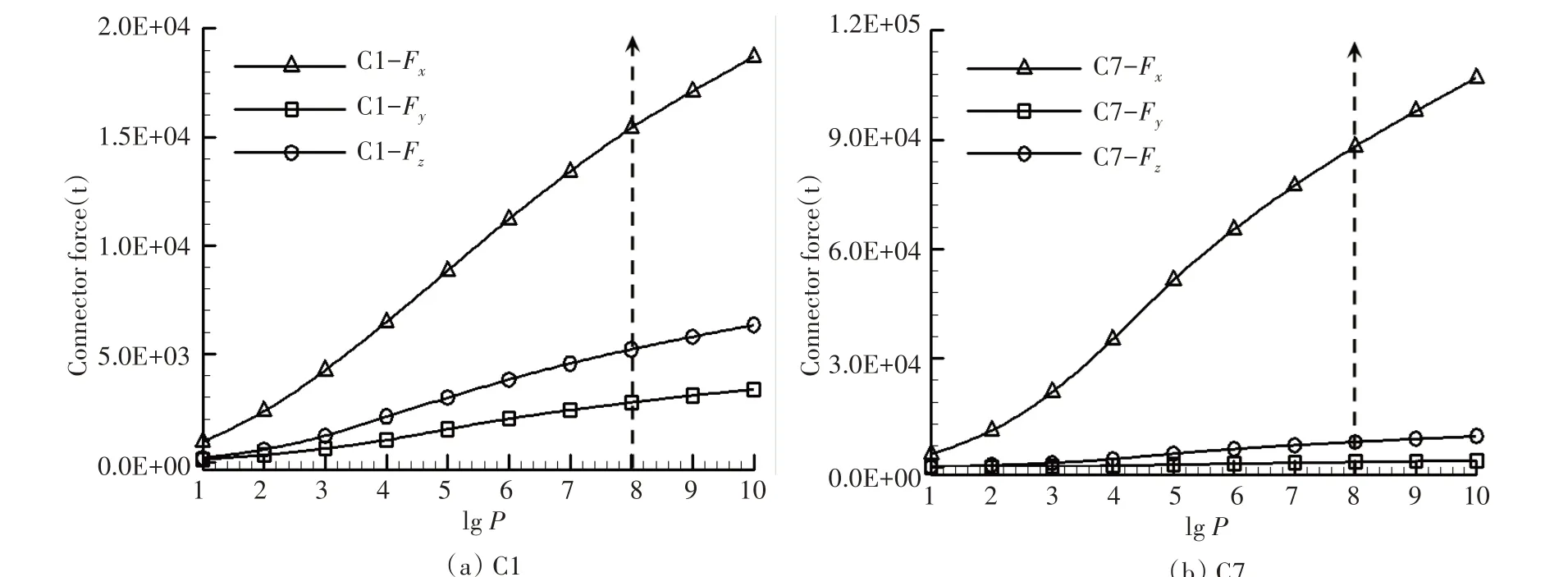
图9 连接器载荷响应长期预报结果Fig.9 Long term predictions of the connector load

4 结 论

当超大型浮体布置在具有复杂海底地形的岛礁附近海域时，将面临现有传统基于深水或有限水深Green函数的势流模式不再适用、遭遇非均匀波浪条件及需要考虑岛礁遮蔽和海底复杂海底地形影响等难题。本文引入水波模型计及复杂环境条件的影响，发展了复杂浅海地形环境中波浪与超大型浮体水弹性响应的直接耦合分析方法，针对一拟布置在岛礁附近的八模块超大型浮体开展了不同布置方案的对比分析，形成如下重要结论：

（1）本文建立的直接分析方法计算结果与模型试验结果吻合良好，可以用来对岛礁海域复杂波浪条件下的超大型浮体动响应进行数值预报。

（2）由于岛礁对波浪传播的遮蔽和绕射作用，使得超大型浮体上实际遭遇的浪向发生了明显的偏转，从而导致了超大型浮体的运动和连接器载荷响应结果出现了明显异于传统无岛礁影响时均匀波浪作用下浮体的响应规律，这间接说明了考虑复杂岛礁环境条件影响的重要性。

（3）通过计算发现，在典型短期海况下，多模块超大型浮体处在中间位置的C7连接器在Fx方向载荷最大，达到了八万吨量级；而Fy和Fz方向的载荷相对较小，都在千吨量级。这给多模块超大型浮体最薄弱环节连接器系统的设计、评估和制造提供了重要参考依据。

总体来说，针对布置在近岸或岛礁附近超大型浮体的动响应分析，需要考虑复杂环境条件及相对岛礁不同布置方案等因素的影响，本文形成的一些初步结论可为后续超大型浮体在近岛礁海域的布置、设计、评估和运营等方面提供一定的技术支撑。