学习数据分析支持的区本精准教研实践探索

◎ 张 敏 王 晴

随着各种技术平台运用于学科教学中，平台所积累的大量数据有助于教师分析和改进教学，也有助于区、校教研工作的有效开展。在此背景下，上海市杨浦区提出提升教研主题的精准性、落实教研功能的实效性的教研工作要求，在项目研究中积极探索区本精准教研的实践路径。

一、建立学习数据分析支持的区本精准教研的实施路径

在信息技术日趋成熟的背景下，要利用数据分析来提升教研的精准性和实效性，需要构建“基于课程标准的小学数学学习过程诊断练习管理系统”（以下简称“诊断练习系统”），明晰数据分析类型和形成有效教研路径。

（一）建立区本精准教研路径的必要前提

1.构建诊断练习系统

诊断练习系统从学科诊断练习关键属性和错因类归两个维度进行构架（见图1）。

诊断练习的属性不仅能助力作业的诊断功能，更能促进练习巩固知识技能、发展学科能力作用的发挥。小学数学学科诊断练习的关键属性包括知识模块、学习水平、学科能力、难度系数等。

在“学习水平”“学科能力”等属性关联下，能较为精准地判定学生学习目标的达成程度。在此基础上若能对学生练习错误现象加以类归分析（见表1），则能更为深入地了解学习目标未达成的原因。

表1 各内容领域单元错因类归汇总表

其中“图形与几何”单元错因类归汇总如表2所示。

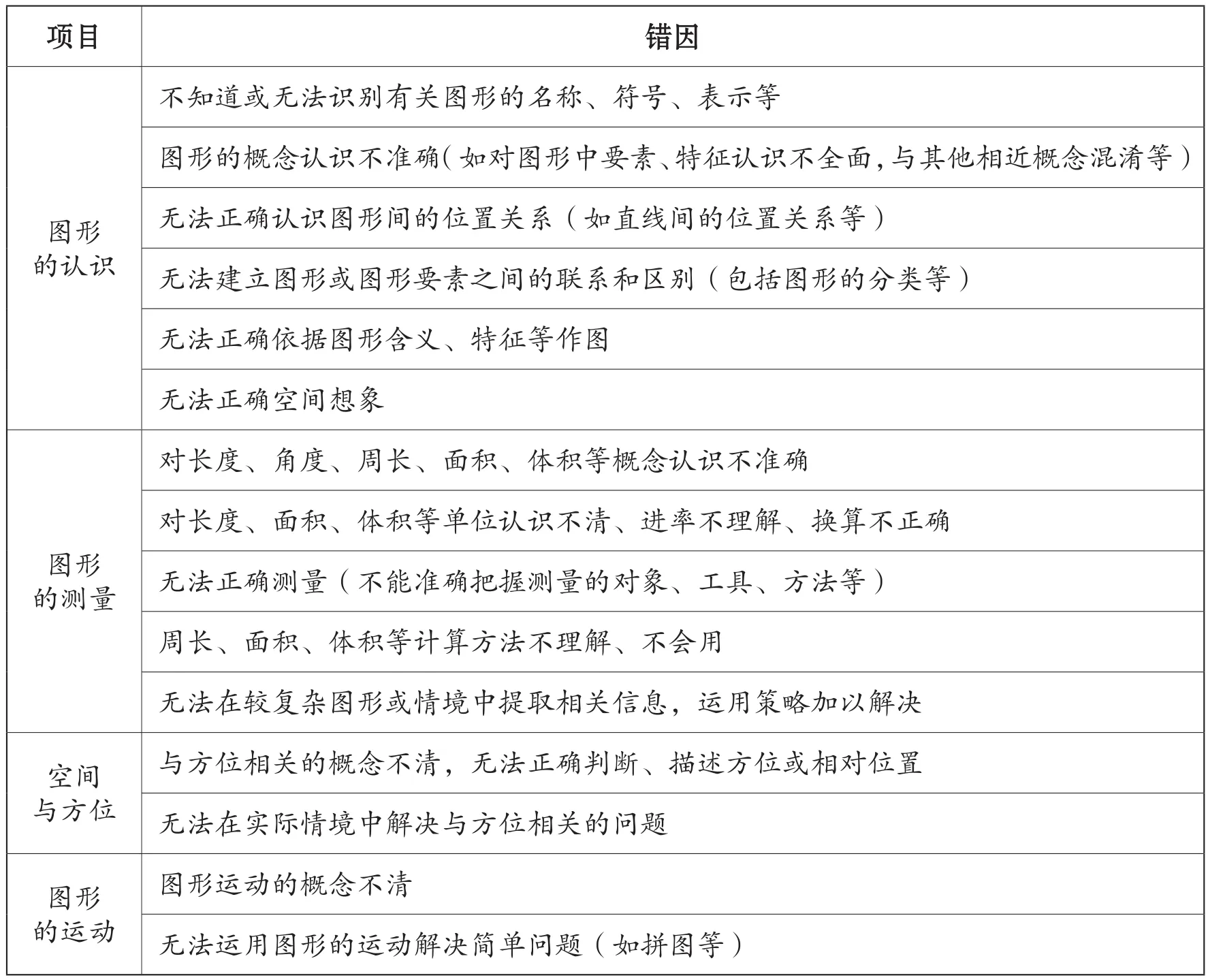
表2 “图形与几何”单元错因类归汇总表

2.明晰诊断练习目标与关键属性关联的数据分析类型

诊断练习系统中的诊断练习均是目标导向下的属性关联设计，为多维度的数据分析与统计提供基础。教师不仅能按课时内容或目标查询该类练习的情况，还能按在单元、学期等查询“学习水平”“学科能力”“难度系数”“错因类归”等维度达成情况，由此可以实现个体与个体、群体与群体、个体与群体间数据的深入对比分析，从而发现问题，探寻原因。

数据分析大致可以分为横向数据分析和纵向数据分析两类。横向数据分析是指对个体与群体中其他个体某一属性的数据进行分析，如一个年级中的一个班级与其他班级的数据比较、一个区域中的一所学校与其他学校的数据比较等。纵向数据分析是指在一定的学习进程中，对个体不同阶段某一属性的数据进行分析，如一个班级、一个年级或一个区域的过程数据分析。

在横向数据分析中，可以进行单点数据比较和多点数据比较，即比较的对象可以是某一个属性分类中的一个类别，也可以是某一个属性分类中的多个类别。图2指向的是单点数据横向比较，图3指向的是多点数据横向比较。

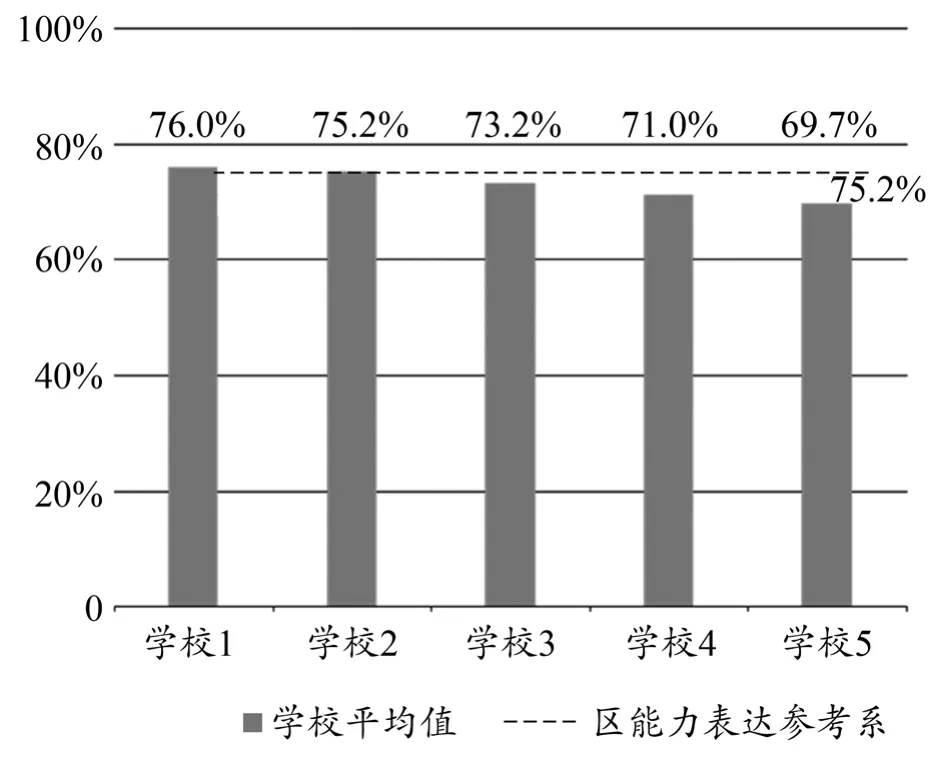
图2 某校数量关系能力达成率比较

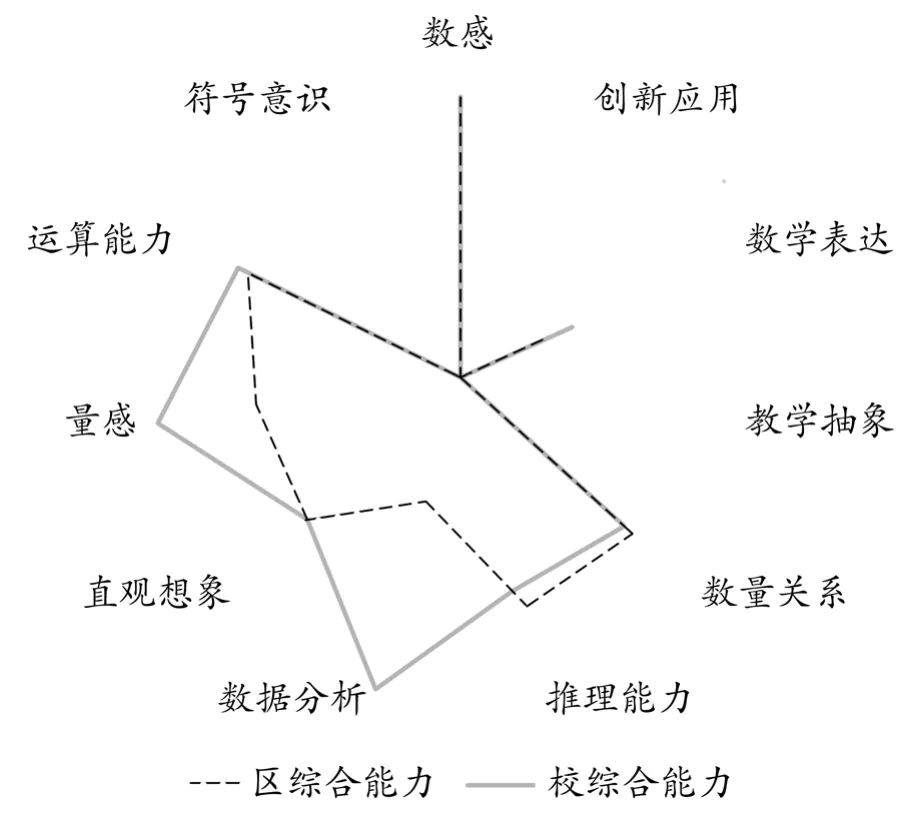
图3 某校各学科能力达成率比较

横向数据对比后，可以发现个体与群体的差异，并通过查找相关的教学目标、内容，分析其教学的具体情况、答题的错误成因等，锚定需改进的关键问题。

在纵向数据分析时，必须准确把握关联点建立学习进程，如同一个单元的不同课时、同一学期不同单元的同一个学科能力、不同学期同一个知识模块等，进行数据相关分析，如此才能有效抓住该类学习进程中的薄弱环节。图4呈现的是某一个班级在图形与几何单元中不同课时的达标情况，发现这个班与年级目标达成率相比，在垂直第4课时突然低于全校平均值。那么这组数据就需要引起关注，进而通过对诊断练习的学习水平、难易系数、学科能力、错误成因等属性的分析，查找原因并及时改进。

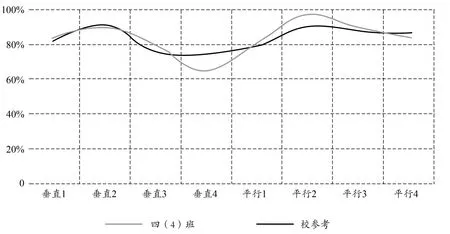
图4 某校四年级（4）班“图形与几何”单元课时诊断目标达成率走势图

（二）形成区本精准教研路径构建的基本思路

诊断练习系统开发的根本目的是助力教研的精准，为改进教学提供明确方向，为教研的成效提供证据。本区形成基于学习数据支持的精准教研基本路径（见图5）始于对诊断练习系统中练习的“知识板块”“认知水平”“学科能力”“难易程度”等属性的目标达成判断，目标未达成则关联错因类归，分析课堂教学中“活动设计”“核心问题”“学习资源”“学生表现”等方面可能存在的问题，结合教学经验确定目标未达成的原因，拟定教研主题，思考教学改进方案。接着实施改进性课堂教学，并再次运用诊断练习系统判断目标达成度，检验改进效果。

图5 学习数据分析支持的区本教研路径

值得注意的是在“研究教学改进方法”和“课堂教学再实施”间有一个环节——“选择数据分析策略”，只有在教学实施前对数据分析样本的选择有充分的思考和准备，才能保障后续数据分析结果的真实和有效。区项目组在实践的基础上提炼了“依据整体数据分析改进教学”和“依据分层数据分析改进教学”两种数据分析策略。当依据教学经验判断出新设计的教学明显优于以前的教学时，则采用群体数据纵向分析进行检验实证，即对新的教学设计实施前后的学生群体数据进行对比分析。当仅依据教学经验无法精准判定哪一种教学设计更好时，可采用实验班和对照班群体数据横向对比分析的策略。而当预判到群体数据可能没有明显差异，则需对学生群体的学习基础、风格、特质等进行分层数据横向对比分析。因此在实施教学研究前，需要作出严谨的数据分析方案。

二、学习数据分析支持的区本精准教研实践

依照学习数据分析支持的区本精准教研的路径，下文将以“角的度量”一课为例具体呈现其实施过程。

（一）了解学习目标达成度，进行原因分析

教师执教“角的度量”一课前，在“诊断练习系统”上查阅了往年本市学生在学习“角的度量”后的练习情况，发现了具有分析价值的数据（见表3）。

表3 练习属性分析

对于难度系数为1级的练习正确率不到70%，说明学生在“角的度量”这节课的学习中存在困难。通过错因归类发现是学生不能准确把握与使用测量工具并进行正确的测量，再对具体教学内容深究后明晰学习目标未达成的原因有两个。其一，受测量工具的影响，线段测量经验产生负迁移。学生在学习角的度量之前，已经有线段测量的经验。虽然测量长度时“度量单位叠加”经验与测量角度本质上是一致的，但由于测量度量的对象特征不同，学生测量长度的经验又会对测量角度带来负面影响，即受测量“从头”开始量的经验影响，在量角时则会出现将角的顶点与量角器半圆的左端重合的错误（见图6）。其二，量角器构造的复杂性，使内圈、外圈刻度混淆。特别是接近90°的角的测量，如85°、97°等，学生容易看错度数。

图6 学生错误测量方法

（二）提炼教学研究主题，拟定教学改进的方法

找准学习目标未达成的问题后，针对第一个问题，提炼出“学习经验的迁移与再建构促进学生理解水平的提升”的教研主题。通过研讨决定增加一个注重对直尺与量角器两种工具的结构与测量方法进行建构的教学环节，对教学中的学习活动和核心问题展开设计。整个教学改进是“回忆线段测量方法后观察、讨论直尺与量角器构造的异同”；核心问题是“直尺与量角器都有刻度，它们的每一小格表示的量一样吗？”“直尺和量角器都有0起点，那么它们测量的起点分别在哪里？”“中心点在量角器上的作用是什么？”等。

针对第二个问题，提炼了“学习资源的呈现方式对于不同学习层次学生的影响”的教研主题。通过研讨决定设计“单圈”量角器的学习资源，通过从“单圈”到“双圈”量角器的认知过程，理解其设计与使用的原理。

（三）选择数据分析策略，实施教学改进实践并检验教研效果

1.依据群体数据分析的教学改进

教师依据儿童的认知特点和规律预判，关注对直尺与量角器两种工具的结构与测量方法进行建构的教学环节能够促进学生理解水平的提升，因此采用群体数据分析的教学研究策略。为确保数据的真实和可靠，选取了三所不同学校各两个教学班，进行教学改进实践和整体数据分析。数据分析后发现，三所实验校六个实验班相关练习的准确率达到了80.2%。通过学生群体数据验证了教师的教学经验判断。

2.依据分层数据分析的教学改进

关于第二个教研主题，教师们出现不同的预判，因此采用了分层数据分析的研究策略。为了把握学生认知起点以及了解两种教学方法对于不同层次学生的影响情况，除了将六个班级分为三个实验班和三个对照班外，还设计了前测，根据教学内容及教学目标，围绕“角的认识”（见图7）、“线段的测量经验”（见图8）两个方面的检测，将六个班级按学生学习基础分为甲、乙、丙三类。

图7 “角的认识”课前测

图8 “线段的测量经验”课前测

课堂教学实施后，通过课后测4（见图9）分析三类学生的表现：本练习中B、C两个错误选项值的归因各不相同。B选项的错误成因在于对数据变化的趋势判断错误，C选项的错误成因在于内外圈的选择错误。实验班与对照班乙层学生对于C选项的选择比率基本持平；而实验班丙层学生对于C选项的选择比率比对照班降低了11%。这个数据说明，从单圈过渡到双圈的教学方法，能够提升丙层学生对于量角器内外圈刻度的运用水平。可见，这样的数据分析能够帮助教师更为精准地进行教学分析，在班级存在学习基础差异的情况下，直观地比较不同的教学设计对不同学习基础的学生所产生的效果。

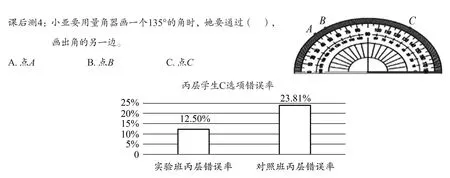
图9 丙层学生课后测第4题C选项占比情况

三、反思与展望

经历了一年的研究与实践，区学科教研质量有了很大的提高，有效地促进了教师学科教学能力的发展。但由于研究时间较短，还存在一些需要思考和解决的问题，如每个课时练习在难易度上并不均衡，学科能力的覆盖面不广；积累的教研案例还不丰富等。后续区项目组将从以下三个方面进行深化研究，一是从练习编制的质量着手，使每个课时编制的练习涵盖的属性变得更均衡，已达成精准诊断的目的；二是现阶段的诊断练习以客观题为主，为能更好地诊断学生的学科素养发展，需要编制一些类似“一题多解”的主观题，以突破客观评价无法满足对学生个性化表现进行诊断的瓶颈；三是需要不断地利用现有的路径开展精准教研的实践，在优化路径的同时积累更多的典型案例。