离散延迟观测系统状态和离散观测模态的混杂随机时滞系统的反馈镇定问题
2022-03-23王思敏陆见秋毛学荣
王思敏, 陆见秋, 毛学荣
(1.东华大学 理学院, 上海 201620; 2.思克莱德大学 数学与统计系, 格拉斯哥 G1 1XT)
混杂随机微分方程被广泛用于描述具有可变结构且易受随机突变影响的实际系统,例如受环境扰动的传染病模型和宏观调控下的金融模型,为了实现这类系统的自动控制,学者们对系统的稳定性进行了大量的研究与分析[1-6]。
在实际应用中,由于传输速度的限制,动态系统(例如神经网络和复杂动态系统)中不可避免地存在时滞,而时滞的存在通常会对系统的稳定性产生负面影响,因此,近年来含时滞系统的稳定性分析与自动控制问题引起了学者们的广泛研究[7-13]。
反馈控制是自动控制中一种镇定系统(通过加入控制器使不稳定的系统稳定)的有效方式。为了降低控制成本,2013年,Mao[14]在经典的连续时间观测系统状态和模态的反馈控制器的基础上,开发了一种基于系统状态离散观测值设计的反馈控制器(只需要在固定的时间点对系统状态进行观测),在全局Lipschitz条件下,用比较定理证明了受控系统的均方指数稳定性,并给出了观测间隔τ的上界。2014年,Mao等[15]从系统本身的性质出发,在同样的条件下证明了受控系统的均方指数稳定性,并给出了τ的更优上界。2015年,You等[16]在局部Lipschitz条件下引入了一个Lyapunov泛函,从而研究了受控系统的几乎必然渐近稳定性,并再次优化了τ的上界。考虑到在实际应用中,观测系统状态设计控制器时,无法避免地会产生延迟,Qiu等[17]和Zhu等[18]在文献[14-16]的基础上考虑离散延迟观测系统状态,从而设计反馈控制器,研究了含延迟的控制器作用下受控系统达到稳定的充分条件。
上述文献中讨论的反馈控制器仍然是利用系统模态当前的值进行设计的,然而,在很多现实问题中,系统当前的模态是未知的,因此,设计控制器时连续观测系统模态也是相当耗费成本的。为了进一步节约控制器的成本,学者们开始考虑设计同时离散观测系统状态和模态的控制器。Geromel等[19]从数值角度论证了同时离散观测系统状态和模态的必要性。Li等[20]证明了小区间上马尔可夫跳发生的概率有界性,并利用系统状态和模态的离散观测值设计了反馈控制器,使受控系统达到均方指数稳定。
目前,还未有相关文献考虑利用系统状态和模态同时离散观测且状态观测带有延迟的反馈控制器从而镇定混杂随机时滞系统。本文综合考虑设计此类离散时间和状态延迟观测的控制器,以期使控制后的随机系统达到多种意义下的稳定。
1 符号与问题表述
1.1 预备知识
本文中(Ω,,{t}t≥0,P)为一个完备概率空间,其中域流{t}t≥0是递增且右连续的,并且0包含所有P空集。令w(t)=(w1(t),…,wm(t))T为定义在以上完备概率空间中的m维布朗运动[6]。若x∈Rn,则用|x|表示其欧几里德范数。若A是一个矩阵,则用AT表示其转置,用表示其迹范数,用‖A‖=max{|Ax|∶|x|=1}表示其算子范数。若A是一个对称矩阵(A=AT),则分别用λmin(A)以及λmax(A)表示其最小和最大特征值,分别用A≤0以及A<0表示A是半负定或负定矩阵。如果a,b均为实数,则令a∨b=max{a,b}且a∧b=min{a,b}。若A是Ω的子集,则用IA表示其特征函数,即当ω∈A时IA(ω)=1,否则IA(ω)=0。令C([-u,0];Rn)是一族有界的,其中0是可测的,取值为C([-u,0];Rn)中的随机变量。若x(t)是定义在t∈[-u,∞)上取值在Rn中连续的随机过程,则当t≥0时,令xt={x(t+θ):-u≤θ≤0},并将其视为取值在C([-u,0];Rn)中的随机过程。
令r(t)(t≥0)为概率空间中取值在有限状态空间S={1,2,…,N}中的右连续马尔可夫链。给定其生成元Γ=(γij)N×N为
P{r(t+Δ)=j|r(t)=i}=

1.2 问题表述
考虑一个n维混杂随机变时滞微分方程(stochastic differential delay equation,SDDE):
dx(t)=f(x(t),x(t-h(t)),r(t),t)dt+
g(x(t),x(t-h(t)),r(t),t)dw(t)t≥-τ*
(1)
其中
f:Rn×Rn×S×R+→Rn,
g:Rn×Rn×S×R+→Rn×m,

本文旨在设计一个离散反馈控制u(x(δt-τ0),r(δt),t)使得受控混杂SDDE如式(2)所示。
dx(t)=(f(x(t),x(t-h(t)),r(t),t)+
u(x(δt-τ0),r(δt),t))dt+
g(x(t),x(t-h(t)),r(t),t)dw(t)
(2)
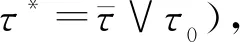
为了研究受控混杂SDDE(式(2))的稳定性,给出以下假设。
假设1假设系数f和g满足局部Lipschitz和线性增长条件。


成立。
(2)线性增长条件:存在常数L>0使得对所有的(x,y,i,t)∈Rn×Rn×S×R+有
|f(x,y,i,t)|∨|g(x,y,i,t)|≤L(|x|+|y|)
成立。
由该假设可知,对所有的(i,t)∈S×R+有f(0,0,i,t)=0,g(0,0,i,t)=0成立。
假设2假设存在一个正常数K使得对所有(x,y,i,t)∈Rn×Rn×S×R+有
|u(x,i,t)-u(y,i,t)|≤K|x-y|
成立,且对所有(i,t)∈S×R+有u(0,i,t)=0成立。
根据该假设,令y=0,可知u满足线性增长条件,即对所有(x,i,t)∈Rn×S×R+有
|u(x,i,t)|≤K|x|
成立。
为建立本文中的定理体系,对于受控混杂的SDDE(式(2)),需要以下额外信息:xη={x(η),-2τ*-2τ≤η≤-τ*},但这些xη的具体值并不影响定理的结果,因此本文设置系统初值为ξ∈C([-2τ*-2τ,0];Rn)以及r0∈S。同时定义常数:观察到对于受控混杂SDDE(式(2)),若定义和ζ3:[0,∞)→[0,τ+τ0]为
ζ1(t)=h(t)t∈[0,∞)
ζ2(t)=t-kτ,kτ≤t<(k+1)τ,k=0,1,2,…
ζ3(t)=t-kτ+τ0,kτ≤t<(k+1)τ,
k=0,1,2,…
则式(2)可写为
dx(t)=(f(x(t),x(t-ζ1(t)),r(t),t)+u(x(t-ζ3(t)),r(t-ζ2(t),t))dt+g(x(t),x(t-ζ1(t)),r(t),t)dw(t)
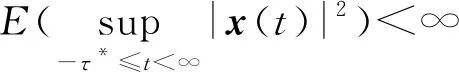
2 主要结论
2.1 渐近稳定性
为了建立受控混杂SDDE(式(2))在不同意义下稳定的充分条件,首先构造一个Lyapunov泛函:
x(v-h(v)),r(v),v)+
u(x(δv-τ0),r(δv),v)Iv≥0|2+
|g(x(v),x(v-h(v)),r(v),v)|2]dvds
t≥0
(3)

{x(s)∶-2τ*-2τ≤s≤0}=φ∈
C([-2τ*-2τ,0];Rn),r(s)=r0,
f(x,y,i,s)=f(x,y,i,0),u(x,i,s)=
u(x,i,0),g(x,y,i,s)=g(x,y,i,0)。
对于U∈C2,1(Rn×S×R+;R+),定义算子LU:Rn×Rn×S×R+→R:
(4)
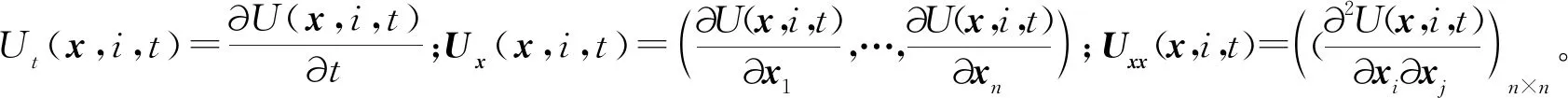
下面给出关于U的假设。
假设3假设存在函数U∈C2,1(Rn×S×R+;R+)以及3个正数λ1、λ2以及λ3使
LU(x,y,i,t)+λ1|Ux(x,i,t)|2≤
-λ2|x|2+λ3|y|2
(5)
对所有(x,i,t)∈Rn×S×R+,(x,y,i,t)∈Rn×Rn×S×R+成立。
在说明结果之前,依次给出一个引理和定理。
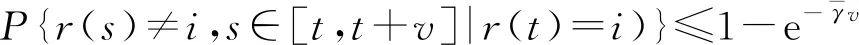
定理1令假设1、假设2以及假设3成立。假设存在正定对称矩阵Pi(i∈S)使得λ2>λPM∶=maxi∈Sλmax(Pi),λ3≤λPm∶=mini∈Sλmin(Pi)。令
(6)
若τ>0,τ0>0充分小,且满足
(4(τ+τ0)+2)L2+4θ(τ+τ0)2K2+λPM
(7)
则对于任意初值φ∈C([-2τ*-2τ,0];Rn)以及r0∈S,受控混杂SDDE(式(2))在均方意义下是H∞稳定的,即
(8)
证明:给定φ∈C([-2τ*-2τ,0];Rn)以及r0∈S,将受控混杂SDDE(式(2))的解x(t)看成是过程,对式(3)中定义的Lyapunov泛函使用广义公式[6],则有
(9)
其中M(t)是初值为M(0)=0的连续鞅。根据假设1、假设2、引理1以及条件(7)易知
(10)
其中
τ0)(4(τ+τ0)+2)L2-4θ(τ+τ0)2K2-λPM。
注意到t-δt+τ0≤τ且当t f(x(s),x(s-h(s)),r(s),s)+u(x(δs-τ0),r(δs), s)Is≥0|2+|g(x(s),x(s-h(s)),r(s),s)|2]ds, 当0≤t r(s),s)+u(x(δs-τ0),r(δs),s)Is≥0]ds+ 综上可得, f(x(s),x(s-h(s)),r(s),s)+u(x(δs-τ0),r(δs),s)· Is≥0|2+|g(x(s),x(s-h(s)),r(s),s)|2]ds (11) 对任意t≥0成立。令 则由式(10)和(11)可推出 (12) 由条件式(7)可知λ>0。又根据式(9)可知 (13) 其中 θ(τ+τ0)2[(4(τ+τ0)+2)L2+(τ+τ0)K2]‖φ‖2 是正数。则由式(13)可得 即式(8)成立。证毕。 (14) (15) 则受控混杂SDDE(式(2))的解对于任意t≥0,均满足 (16) 证明:由定理1的证明可知,x(t)和x(δt-τ0)在0≤t 首先,考虑t≥kτ的情形。令n≥k为整数,则δt-τ0=nτ-τ0≥0对任意t∈[nτ,(n+1)τ)成立,在这种情形下,可以得到 (17) 另外注意到 (18) 将式(18)代入式(17)可得 (19) 由Gronwall不等式可得 (20) 然后,考虑0≤t 显然该式与式(19)一致。因此式(20)对0≤t 整理可得 (21) 定理2假设定理1和引理2中的条件均成立,则受控混杂SDDE(式(2))均方渐近稳定,即 对任意初值φ∈C([-2τ*-2τ,0];Rn)以及r0∈S成立。 证明:给定φ∈C([-2τ*-2τ,0];Rn)以及r0∈S。根据公式,当t≥0时,有 根据假设1及假设2可知 x(δs-τ0)|2ds, 该处以及下文中的C代表一个正数,它的取值可随着项的不同而改变。由引理2可得(令α=0) (22) 又 将上式代入式(22)并应用定理1的结论可知,存在正数C,使得对任意t≥0都有 E|x(t)|2≤C [f(x(t),x(t-h(t)),r(t),t)+u(x(δt-τ0), r(δt),t)]+|g(x(t),x(t-h(t)),r(t),t)|2)dt≤ 对任意0≤t1 |E|x(t2)|2-E|x(t1)|2|≤C(t2-t1) 即E|x(t)|2在t∈R+关于t一致连续。 第2.1节构造的状态和模态同时离散的反馈控制器讨论了混杂SDDE(式(1))的渐近稳定性问题,并证实了当t趋于∞时,E|x(t)|2将趋近于0,但不知道E|x(t)|2趋于0的速率。本节为研究E|x(t)|2以及x(t)趋向于0的速率,对混杂SDDE(式(1))的指数稳定性进行研究。首先,给出以下假设。 假设4假设存在两个正数c1,c2使得 c1|x|2≤U(x,i,t)≤c2|x|2 对所有(x,i,t)∈Rn×S×R+成立。 定理3令假设1~4以及引理1成立,θ定义同式(6),令 (4(τ+τ0)+2)L2-4θ(τ+τ0)2K2-λPM(λ>0) (23) 且 (24) 其中,γ>0是方程 (τ+τ0)γe(τ+τ0)γ(H1+ (25) 的唯一解,该方程中 H1=4θ(τ+τ0)2(L2+K2)+2θ(τ+τ0)L2, H2=2θ(τ+τ0)L2(2(τ+τ0)+1), H3=4θ(τ+τ0)2K2 (26) 其中t≥0。根据Lyapunov泛函的定义式(3)以及式(12)和(13),可推得 (27) 令 u(x(δv-τ0),r(δv),v)|2+|g(x(v), x(v-h(v)),r(v),v)|2]dvds。 则由式(3)及假设4可知 (28) 首先,由假设1、假设2及引理2可得 H2E|x(v-h(v))|2+ H3E|x(v)-x(δv-τ0)|2Iv≥0]dv (29) 其中,H1、H2、H3的定义如式(26)所示。将式(29)代入式(28),并将结果进一步代入式(27)可得,对于z≥τ+τ0,有 (30) 其中, (31) (32) (33) 代入式(30)可得 又式(25)成立,故对任意t≥τ+τ0都有 c1eγtE|x(t)|2≤C 成立,显然该定理中结论式(23)成立。根据Mao等[6]的研究结论,可由式(23)得到该定理中的另一结论即式(24)。证毕。 在实际应用中,二次型常被用于构造Lyapunov函数。本节使用二次型U(x,i,t)=xTQix,其中Qi是n×n阶对称正定矩阵。令c1=mini∈Sλmin(Qi),c2=maxi∈Sλmax(Qi),假设4显然成立。进一步给出以下假设。 假设5假设存在对称正定矩阵Qi∈Rn×n(i∈S)以及两个正数λ4和λ5,使得对所有的(x,i,t)∈Rn×S×R+以及(x,y,i,t)∈Rn×Rn×S×R+都有 2xTQi[f(x,y,i,t)+u(x,i,t)]+ trace[gT(x,y,i,t)Qi(x,i,t)g(x,y,i,t)]+ (34) 成立。 根据上述假设,可以立刻得到定理3的推论。 推论1若假设1、假设2以及假设5成立。令 c1=mini∈Sλmin(Qi),c2=maxi∈Sλmax(Qi), λ6=2maxi∈S‖Qi‖, 在推论1的基础上,给出如下算例: 例1考虑一个线性不稳定混杂SDDE: dx(t)=(A(r(t))x(t)+Ad(r(t))· x(t-h(t)))dt+(B(r(t))x(t)+ Bd(r(t))x(t-h(t))dw(t)t>0 (35) 系统中的矩阵分别为 混杂SDDE(式(35))并不是均方指数稳定的。因此要构造一个基于状态和模态的离散观测的反馈控制器。假设受控混杂SDDE的形式如式(36)所示。 dx(t)=(A(r(t))x(t)+Ad(r(t))x(t-h(t))+ F(r(δt))G(r(δt))x(r(δt-τ0)))dt+ (B(r(t))x(t)+Bd(r(t))x(t-h(t))dw(t)。 (36) 选定 则可以求得 0.910 5>1 152(1-e-τ-τ0)+21 256.240 4(τ+τ0) (4(τ+τ0)+2)+331 776(τ+τ0)2+0.5, 21 256.240 4(τ+τ0)(4(τ+τ0)+2)≤0.14, τ+τ0≤0.020 8。 (37) 式(37)只有在τ+τ0<0.000 220 7时才成立。 根据推论1,若令Fi和上文给定的一样,同时确保τ+τ0<0.000 220 7,则该例中基于状态和模态同时离散的受控SDDE(式(36))呈均方指数稳定且几乎必然指数稳定。电脑仿真结果(见图1)也表明该结论成立。 图1 用Euler-Maruyama方法估计混杂SDDE(式(36))的路径(步长为10-6,初值 x1(0)=2,x2(0)=2,r(0)=1) 本文构造了利用系统状态和模态同时离散观测且状态观测带有延迟的反馈控制器,研究了非线性变时滞混杂系统的镇定问题。通过构造Lyapunov泛函,建立了非线性变时滞混杂系统在均方意义下H∞稳定、渐近稳定和指数稳定的充分条件。此外,得到了两次状态和模态观测时间间隔的上限。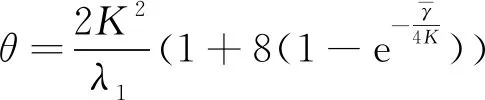





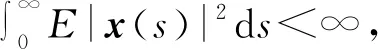
2.2 指数稳定性



3 算 例
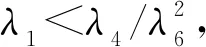
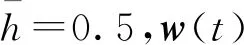
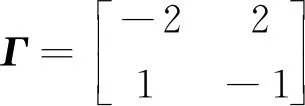


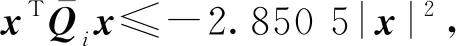

4 结 语
