高度非线性比例型混杂随机微分方程的时滞反馈镇定
2022-03-23马雪茹尤苏蓉
马雪茹, 尤苏蓉
(东华大学 理学院, 上海 201620)
随机时滞微分方程(stochastic delay differential equations, SDDEs)被广泛应用于随机时滞系统的建模分析[1-6]。事实上,这些系统的结构和参数往往会发生突变,故引入连续时间马尔科夫(简称“马氏”)过程来模拟这些突变,从而产生了具有马氏切换的 SDDEs,即混杂SDDEs。在局部Lipschitz条件和线性增长条件下,混杂SDDEs的解存在且唯一[7]。但在实际应用中,很多随机系统不满足线性增长条件,针对这类高度非线性混杂SDDEs,当系数满足Khasminskii型条件时,解的存在唯一性、稳定性问题得到了较为广泛的研究[8]。此外,稳定化分析也是微分方程研究的一个重要问题。考虑一个不稳定的随机系统,为使该随机系统变得稳定,经典方法是根据被控系统的当前状态找到一个反馈控制器,使得受控系统稳定。然而,鉴于状态观测与反馈控制到达系统之间存在时间间隔,依赖于过去状态的控制则更为合理,因此反馈控制器应为时滞反馈控制器。自文献[9]建立了一个关于高度非线性混杂SDDEs的时滞反馈控制新理论以来,不同类型微分方程的相关问题受到学者的广泛重视。例如,文献[10]讨论了基于离散时间观测反馈控制的高度非线性混合随机微分方程的稳定,文献[11]通过反馈控制讨论了高度非线性中立型混杂随机微分方程的稳定等。
比例型随机微分方程(pantograph stochastic differential equations, PSDEs)是一类具有无界延迟的特殊随机微分方程,在机械、生物、工程和金融等领域中得到了广泛应用。文献[12-16]讨论了PSDEs的存在唯一性和稳定性。但当给定的系统是高度非线性时,能否设计一个时滞反馈控制使得受控后PSDEs稳定,这一问题目前还没有结论。因此,有必要建立一个新的理论来说明如何设计时滞反馈控制来稳定高度非线性混杂PSDEs。本文旨在设计一个时滞反馈控制来稳定一类系数满足Khasminskii型条件的高度非线性比例型混杂随机微分方程。
1 问题背景及相关记号
设(Ω,,{t}t≥0,P)是一个完备概率空间,{t}t≥0是其上的一个σ域流,满足通常条件(即单调递增且右连续,0包含所有的P-零测集)。B(t)=(B1(t),B2(t),…,Bm(t))T是定义在该概率空间上的m维布朗运动。对于x∈n,用|x|表示其欧几里得范数。若A是一个向量或者矩阵,使用AT表示其转置,用表示它的迹范数。对于两个实数a和b,记a∨b=max(a,b),a∧b=min(a,b)。
令r(t),t≥0是该概率空间上的一个右连续的马尔科夫链(简称马氏链),取值于有限状态空间S={1,2,…,N},其生成矩阵Γ=(γij)N×N定义为

考虑如下的比例型混杂随机微分方程
dx(t)=f(x(t),x(θt),r(t),t)dt+g(x(t),x(θt),r(t),t)dB(t),t≥0
(1)
初值条件为
x(0)=x0∈n,r(0)=i0∈S
(2)
其中f:n×n×S×+→n,g:n×n×S×+→n×m分别为方程的漂移系数和扩散系数,0<θ<1为比例系数。假设方程(1)的两个系数f和g满足局部Lipschitz条件。
假设1假设对任意实数h>0,存在Kh>0 使得对任意关于(i,t)∈S×+,有
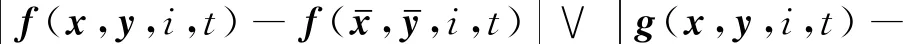
(3)
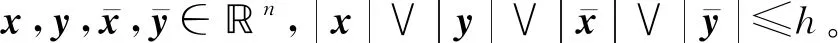
且存在常数K>0,q1>1及qi≥1(2≤i≤4)使得对任意(x,y,i,t)∈n×n×S×+,有
(4)
假设1保证式(1)具有唯一的最大局部解,该局部解可能在有限时间内爆破。为避免这种可能的解爆破,需要施加以下Khasminskii条件。
假设2假设存在一组常数p,q,α1,α2,α3,α4,满足α3>α4且
q>(p+q1-1)∨(2(q1∨q2∨q3∨q4))
p≥2(q1∨q2∨q3∨q4)-q1+1
(5)
其中,q1,q2,q3,q4如假设1给出,使得对任意(x,y,i,t)∈n×n×S×+有
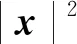
(6)
传统解的存在唯一性定理要求方程系数满足局部Lipschitz条件和线性增长条件。在局部Lipschitz条件和Khasminskii条件下,方程具有非线性特征,引理1给出了这类方程解的存在唯一性。
引理1[13]若假设1和2成立,则对式(2)给出的初值条件,方程式(1)在t∈[0,∞)上存在唯一的解x(t)。
虽然式(1)的解在假设1和2的条件下是有界的,但是方程可能不稳定。在这种情况下,需要设计一个时滞反馈控制u(x(t-τ),r(t),t)使得受控方程式(7)变得稳定。
dx(t)=[f(x(t),x(θt),r(t),t)+u(x(t-τ),
r(t),t)]dt+g(x(t),x(θt),r(t),t)dB(t)
(7)
其中,控制器u:×S×+→n为Borel可测函数。为了进一步讨论需要,对方程式(7)加上初值条件,如式(8)所示。
{x(t):-2τ (8) 同时,本文设计的控制函数将满足假设3。 假设3存在一个正数κ,对所有x,y∈n,i∈S,且t≥0有 |u(x,i,t)-u(y,i,t)|≤κ|x-y| (9) 此外,假设u(0,i,t)≡0。 也就是说,控制函数u(x,i,t)关于x是全局Lipschitz连续的,这个假设隐含了线性增长条件,如式(10)所示。 |u(x,i,t)|≤κ|x|∀(x,i,t)∈n×S×+ (10) 定理1在假设1和2条件下,若控制函数u满足假设3,则对式(8)给出的初值条件,方程式(7)在t∈[-τ,∞)上存在唯一的解x(t),且解x(t)具有性质: 其中ε>0为方程β3+β4=ε+β3θ-ε+(1+τ)ε的唯一解,β3,β4,C由式(13)定义。 证明对任意(x,i,t)∈n×S×+,取V(x,i,t)=,定义函数LV(x,y,z,i,t):n×n×n×S×+→ 由假设2和3有 (11) 取正数α<α3-α4及α5<α3-α4-α,利用Young不等式,方程式(11)可进一步变为 (12) 其中 β4=qα5 (β2-β3-β4)uq+p-2}<∞ (13) 下面将证明过程分两步完成。 若能证明τ∞=∞,则可以得到σ∞=∞,即方程式(7)在t∈[-τ,∞)上存在唯一解得证。接下来给出τ∞=∞的证明。 EV(x(τk∧t),r(τk∧t),τk∧t)=V(x0,r0,0)+ 将式(12)应用至上式得 EV(x(τk∧t),r(τk∧t),τk∧t)-V(x0,r0,0)≤ θβ3U2(x(θs),θs)+β4U2(x(s-τ),s-τ)}ds 对任意(x,t)∈n×+,取U1(x(t),t)=则有 U1(x(t),t)≤V(x,i,t)≤U2(x(t),t) (14) 从而可以得到 EU1(x(τk∧t),r(τk∧t),τk∧t)≤U2(x0,0)+ τ),s-τ)ds≤K1+Ct (2)对(1+t)εV(x(t),r(t),t)应用It公式。对t≥0有 E{(1+τk∧t)εV(x(τk∧t),r(τk∧t),τk∧t)}- (1+s)εLV(x(s),x(θs),x(s-τ),r(s),s))ds 将式(12)和(14)应用至上式可进一步得到 E{(1+τk∧t)εU1(x(τk∧t),τk∧t)}- U2(x(s-τ),s-τ)ds (15) 从而式(15)可以进一步变为 E{(1+τk∧t)εU1(x(τk∧t),τk∧t)}≤ 又由ε为方程β3+β4=ε+β3θ-ε+(1+τ)ε的唯一解,故 E{(1+τk∧t)εU1(x(τk∧t),τk∧t)}≤ 令k→∞,则 对上式两边同时除以(1+t)ε+1,令t→∞得 由定理1可知,只要控制函数满足假设3,被控制系统(7)保持给定式(1)的有界性。然而,这样的控制可能无法稳定给定的PSDEs。为了使被控系统(7)稳定,需要更仔细地设计控制函数。 假设4设计控制函数u:n×S×+→n,存在实数正数以及非负数使得对所有(x,y,i,t)∈n×n×S×+有 (16) 且 (18) (δ1,δ2,…,δN)T=1-1(1,1,…,1)T 定义函数U:n×S→+为 (19) 对于方程dx(t)=[f(x(t),x(θt),r(t),t)+u(x(t),r(t),t)]dt+g(x(t),x(θt),r(t),t)dB(t) 定义L1U为 L1U(x,y,i,t)=2δi[xT[f(x,y,i,t)+u(x,i,t)]|+ (20) 那么根据文献[4]和假设4可知受控系统是渐近稳定的。但实际应用中,采取时滞状态反馈控制u(x(t-τ),r(t),t)更为合理,也就是说,受控的PSDEs形式应为方程(7)。接下来将分析如何找到τ>0,使得在时滞控制u(x(t-τ),r(t),t)下,方程(7)稳定。 假设5存在8个正数ρj(1≤j≤8)且ρ4>ρ5,ρ6∈(0,1),及函数W∈C(n;+)使得对所有(x,y,i,t)∈n×n×S×+有 (21) 且 (22) 定理2在假设1和2的条件下,若控制函数u满足假设3和4并找出8个正数ρj(1≤j≤8)和函数W∈C(n;+)满足假设5,且进一步保证τ足够小并满足则对式(8)给出的初值条件,方程(7)的解x(t)具有性质: (23) 证明下面将证明过程分三步完成。 (24) dU(x(t),r(t))=L2U(x(t),x(θt), r(t),t)dt+dM(t) (25) L2U(x,y,i,t)=L1U(x,y,i,t)-(2δi+ u(x(t-τ),r(t),t)] 另一方面由 dI(t)=(ζτ[τ|f(x(t),x(θt),r(t),t)+| 可以得到 (26) 其中, [u(x(t),r(t),t)-u(x(t-τ),r(t),t)]+ ζτ[τ|f(x(t),x(θt),r(t),t)+u(x(t-τ),| (27) 综上由定理1和假设1、2、3、5可知 (28) [u(x(t),r(t),t)-u(x(t-τ),r(t),t)]≤ 利用已知条件2ζτ2≤ρ2,ζτ≤ρ3及假设5,式(27)进一步变成 (29) (3)令k0>0为充分大的整数,使‖x0‖ k=inf{t≥0:|x(t)≥k|} 由定理1可知,当k→∞时,k→∞。利用广义It公式,可以由式(26)得到对任意t≥0,k≥k0有 令k→∞,运用Fubini定理和控制收敛定理,对任意t≥0有 式(29)可进一步变为 (30) 另一方面由式(7)有 将上式代入式(30)中可进一步变为 从而有 令t→∞,由假设5得到 推论1在定理2的基础上,将条件ρ6∈(0,1)替换成ρ6=1,则式(7)的解x(t)在初值条件下具有性质: 考虑如下定义在t≥0上的比例型混杂随机微分方程: dx(t)=f(x(t),x(0.5t),r(t),t)dt+ g(x(t),x(0.5t),r(t),t)dB(t) 易知对任意q>6,当q1=3,q2=2,q3=1,q4=1.5,p=4时假设1成立。 对任意(x,y,i,t)∈××S×+有 即对任意q>6,当α1=0,α2=[1+0.01(q-1)2],α3=1,α4=0.04时假设2成立。 假设系统仅在模态1中可观测而模态2中不能,那么仅能在模态1中使用反馈控制。取u(x,1,t)=-4x,u(x,2,t)=0,则当κ=4时,假设3成立。故由定理1得到受控系统在t∈[-τ,∞)上存在唯一的解x(t),且解x(t)具有性质: 为验证假设4,对任意(x,y,i,t)∈××S×+,有 故由式(16)和(17)得 从而假设4成立。 进一步,由式(19)得: 那么L1U(x,y,i,t)≤-x2+0.26y2-0.998 3x4+0.22y4-0.235x6+0.03y6。 又因为|f(x,y,i,t)|2≤x4+y4+8x6,|g(x,y,i,t)|2≤0.02y2+0.02y4 取ρ1=0.2,ρ2=0.006,ρ3=1,则 ρ2|f(x,y,i,t)|2+ρ3|g(x,y,i,t)|2≤ -0.95x2+0.28y2-W(x)+0.402 75W(y) 其中W(x)=0.867 3x4+0.072 5x6。所以当ρ4=0.95,ρ5=0.56,ρ6=0.805 5,ρ7=0.072 5,ρ8=0.506 2时,假设5成立。那么由定理2可知,当τ<0.008 728时,受控系统在控制函数下H∞稳定。 针对高度非线性比例型混杂随机微分方程的稳定化问题,设计一个时滞反馈控制使得受控系统在局部Lipschitz条件和Khasminskii条件下的解存在且唯一,同时给出了这类方程解的有界性。通过一系列技巧对反馈控制进行处理,最终得到受控系统H∞稳定的结论。后续可进一步研究高度非线性比例型混杂随机微分方程的多项式稳定、指数稳定的条件与相关性质。2 主要结果

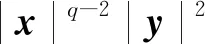

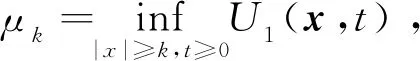
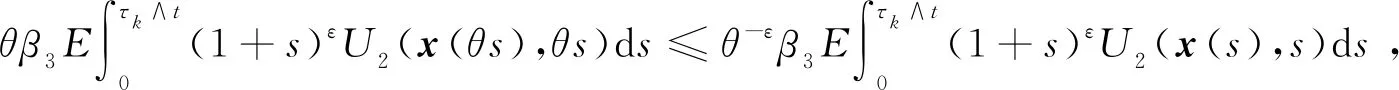
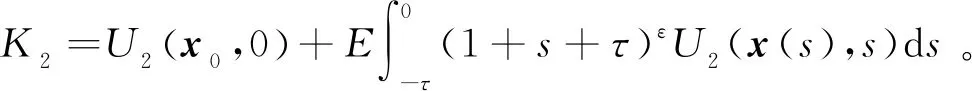
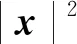

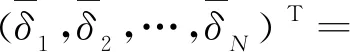
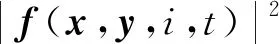
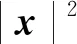
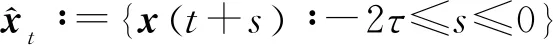
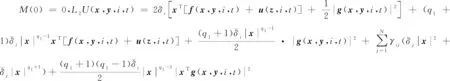

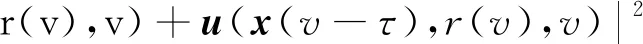
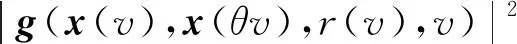
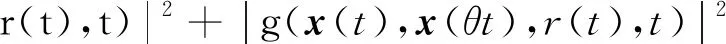
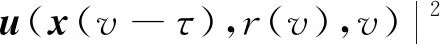
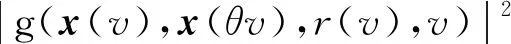
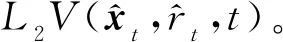
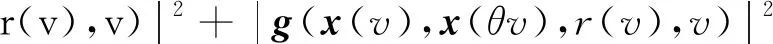
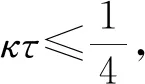


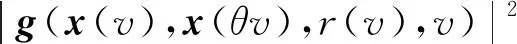


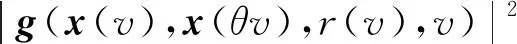

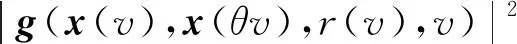


3 算 例
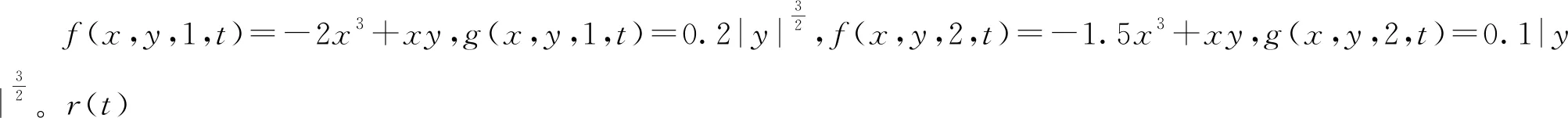

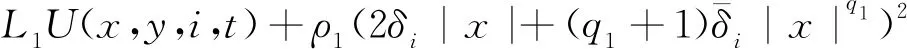
4 结 语
