基于伯努利吸盘抓取经编鞋面稳态过程的研究

何 帆， 孟 婥， 张 豪， 孙以泽

(东华大学 机械工程学院， 上海 201620)

目前在国内制鞋生产线上，鞋面上下料几乎都是人工完成。针对具有透气多孔特性的经编鞋面而言，其质地柔软、透气多孔，导致机械夹爪式和真空吸盘吸附式的抓取方式都不适用于该鞋面上下料。近些年来随着我国人口红利优势的降低和人工劳务费的提高，制鞋行业亟需通过提高制鞋生产线的自动化程度来降低制鞋成本，从而提升企业市场竞争力。

伯努利吸盘是利用伯努利原理开发的非接触式吸盘，其具有低真空、高流量、非接触等特点，适用于搬运轻薄透气型工件，被广泛应用于半导体晶圆、光伏电池领域[1]。目前，国内外研究人员对伯努利吸盘抓取工件进行了相关研究[2-7]，但针对透气性工件的研究比较少。伯努利吸盘抓取经编鞋面过程中存在着动态和稳态两种状态。在动态时，经编鞋面与伯努利吸盘的间距逐渐减小，经编鞋面处于运动上升状态；在稳态时，经编鞋面与伯努利吸盘的间距在足够小的范围内变化，该变化范围几乎可以忽略不计。为解决伯努利吸盘不能稳定抓取经编鞋面问题，本文将通过理论分析、数值模拟和试验研究，对伯努利吸盘抓取经编鞋面稳态过程进行研究，寻找伯努利吸盘稳定抓取经编鞋面最优状态的条件，为利用伯努利吸盘完成经编鞋面上下料提供理论依据和技术指导。

1 伯努利吸盘工作原理

由流体力学可知，流体在流动过程中遵循能量守恒定律，而伯努利方程就是能量守恒定律在流体力学中的一种表达形式[8]。

(1)

式中：p为管道内某一截面的压力；ρ为流体的密度；z为该截面距水平面的距离；g为重力加速度；v为流体流过截面的速度。

由于式(1)等号左边的和为常数，当流速增大时，截面处的压力就会减小。基于该原理，增大出口处的流速，该区域附近的压力就会减小，从而形成负压。

伯努利吸盘工作原理如图1所示。一定压力的空气从吸盘进气口流入，从环型的微小喷嘴高速喷出。利用环型喷嘴沿吸盘锥形内壁喷出的高速气流使吸盘中心产生负压，在外界大气压力的作用下，对工件产生向上的吸附力。高速气流从吸盘与工件的间隙向外排出，使吸盘与工件保持一定的间隙，实现非接触抓取。

图1 伯努利吸盘工作原理图

2 伯努利吸盘抓取经编鞋面稳态过程的理论分析

2.1 多孔介质模型建立

经编鞋面照片如图2(a)所示，从图中可以发现经编鞋面上均匀地分布着许多小孔。为方便研究经编鞋面模型，现以工作直径为60 mm的伯努利吸盘为参考对象，在经编鞋面上任取一个直径为60 mm的圆形区域为研究对象，如图2(b)所示。以直径为60 mm圆的圆心为坐标原点，将经编鞋面分为3个区域，以直径为24 mm圆所围成的区域称为第一区域，以直径为24 mm圆和直径为46 mm圆所围成的区域称为第二区域，以直径为46 mm圆和直径为60 mm圆所围成的区域称为第三区域。经编鞋面上每个小孔直径为1 mm，沿x轴方向相邻小孔间距为4 mm，沿y轴方向相邻小孔间距为3 mm。

图2 经编鞋面及其模型

设直径为60 mm的圆形经编鞋面的面积(包括孔的面积)为Aa,有效面积(未包括孔的面积)为Ae,孔的面积为Ah。由Solidworks软件可以计算出Aa=2 827.43 mm2，Ae=2 647.58 mm2，则该经编鞋面的孔隙率ε为

(2)

多孔介质是流体动力学中一种针对具有多孔性、渗透性的流体区域进行简化计算的模型。当流体经过多孔介质时，会在流动方向上产生压降Δp，包括黏性损失项和惯性损失项两个部分[9]，如式(3)所示，其中等式右边第一项为黏性损失项，第二项为惯性损失项。

(3)

式中：μ为流体黏度；α为多孔介质模型的渗透率；Δn为多孔介质的厚度；v为流体流经多孔介质的流速；C2为惯性阻尼系数；ρ为流体密度。

鉴于经编鞋面具有透气多孔特性，当伯努利吸盘抓取它时，可以将其视为多孔介质模型。

由Ergun方程[10]可计算得经编鞋面渗透率α和惯性阻尼系数C2，如式(4)和(5)所示。

(4)

(5)

式中：Dp为孔隙直径，Dp=1 mm。

2.2 伯努利吸盘抓取经编鞋面稳态下数学模型的建立

为研究伯努利吸盘抓取经编鞋面稳态过程中供气压力、间距对吸附力的影响，建立稳态下的数学模型。伯努利吸盘抓取经编鞋面稳态下的结构示意如图3所示。在吸盘底部中心处O点建立柱坐标系(r,α,z)，在柱坐标下伯努利吸盘抓取经编鞋面稳态过程需要遵循以下假设[11]：

图3 伯努利吸盘抓取经编鞋面稳态下的结构示意图

(1)考虑到间隙内流体的雷诺数Re较小，故认为间隙内的气流状态为层流。

(2)间隙内的气流的黏性影响占主要因素，忽略惯性影响。

(3)将经编鞋面模型简化，视为多孔介质模型。

(4)经编鞋面底面有空气回流现象。

(5)间隙区域内沿垂直方向上没有压力损失。

以经编鞋面的下表面为参考水平面，吸盘入口和出口分别距离参考水平面高度为Z1和Z2，吸盘入口气体流量为Q1、压力为pi，吸盘出口压力为po，经编鞋面底面回流气体流量为Q2，入口和出口的截面积分别为A1和A2，由伯努利方程可得：

(6)

对式(6)整理化简为

(7)

一定压力的气体从吸盘入口进入，然后从喷嘴出口处高速流出，最终沿着吸盘裙边从间隙区域流出。在气体从间隙区域流出的过程中，该区域会出现径向压力损失，包括两部分：(1)气流沿径向扩散所损失的压力降Δp1；(2)由气体黏性作用所导致的压力损失Δp2。故间隙区域的压力损失[1]有

(8)

对于气流沿径向扩散所损失的压力降Δp1，根据伯努利方程有

(9)

忽略高阶小量可以简化为

(10)

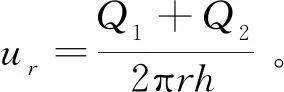
对于由气体黏性作用所导致的压力损失Δp2，将间隙区域简化为气体在两平行壁面之间的平行流动[12]，则有

(11)

因此间隙区域的径向压力损失为

(12)

对式(12)积分得

(13)

考虑到经编鞋面区域内的气体状态是层流，故经编鞋面区域内沿垂直方向上的压力损失可以简化为

(14)

式中：uz为经编鞋面底部回流气体的速度。

考虑经编鞋面底面的回流影响，则间隙区域沿径向的真实压力损失Δpt可以写为

(15)

间隙区域内沿半径方向上的压力分布pr为

(16)

因为间隙区域沿垂直方向上没有压力损失，并且经编鞋面底面附近的压力为大气压，则伯努利吸盘对经编鞋面产生的吸附力F为

(17)

(1)吸附力F与吸盘入口压力pi呈正比例关系。

(2)在一定间距范围内，吸附力F与间距h呈指数函数关系。

(3)吸盘入口与出口的高度差ΔZ或经编鞋面厚度Δn增大，吸附力F增大。

(4)经编鞋面渗透率α减小，其黏性阻尼增大，吸附力F增大。

3 伯努利吸盘抓取经编鞋面稳态过程的数值模拟分析

3.1 简化假设

由于伯努利吸盘与经编鞋面之间的间隙较小，那么从伯努利吸盘出口流出的高速气体经过间隙区域后流场变为层流状态，故对间隙区域的流体和经编鞋面模型作出如下假设[1,11]：

(1)因间隙区域内流场的雷诺数较小，故认为该流场为层流。

(2)忽略空气的惯性影响，即不考虑空气的重力。

(3)流场内的气体与外界没有热交换。

Standard and sample solutions were accurately aspirated in 10 μL aliquots and measured using previously described chromatographic conditions,and the esculetin content was determined to be 97.4%by the external standard calculation method.The chromatography is shown in Figures 2 and 3.

(4)因经编鞋面透气多孔，故将其考虑为多孔介质模型。

3.2 求解方法和初始化

在Fluent软件中采用压力基耦合求解器方法，模型采用标准κ-ε湍流模型，动量采用二阶迎风格式，湍动能和湍流耗散率均采用一阶迎风格式。相比混合初始化，标准初始化可以在计算域里自定义赋初始值，计算收敛性更好[13]，故采用标准初始化。

3.3 几何模型、网格划分及边界条件设置

3.3.1 几何模型

考虑到伯努利吸盘和经编鞋面都呈现轴对称分布，故只需构建四分之一几何模型如图4所示，该几何模型从上到下分别为吸盘内腔区域、间隙区域和经编鞋面区域。

图4 伯努利吸盘抓取经编鞋面的四分之一几何模型

3.3.2 网格划分

考虑到伯努利吸盘内部流体区域形状复杂，故该区域采用适应性更好的四面体网格划分方法。为了更好地使吸盘内腔区域和间隙区域在接触面位置的网格对齐，间隙区域也采用四面体网格划分。考虑到经编鞋面区域形状规则，为了减少迭代计算量，故经编鞋面区域采用Sweep Meshing 划分。整个吸附模型节点个数为98 608，网格单元为420 998，网格质量平均为0.84。

3.3.3 边界条件设置

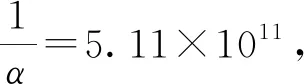
3.4 流场特性分析

3.4.1 间隙区域垂直方向压力分布

当间距h=2.0 mm时不同供气压力下吸附模型中心线沿垂直方向的压力曲线如图5所示。由图5可知：当间距h和供气压力p一定时，间隙区域(y=0～2 mm)沿y轴方向(垂直方向)的压力没有发生变化；当间距h一定，供气压力从0.1 MPa增加到0.6 MPa时，经编鞋面区域(y=2～5 mm)负压由-3.6 kPa增加到-22.0 kPa。

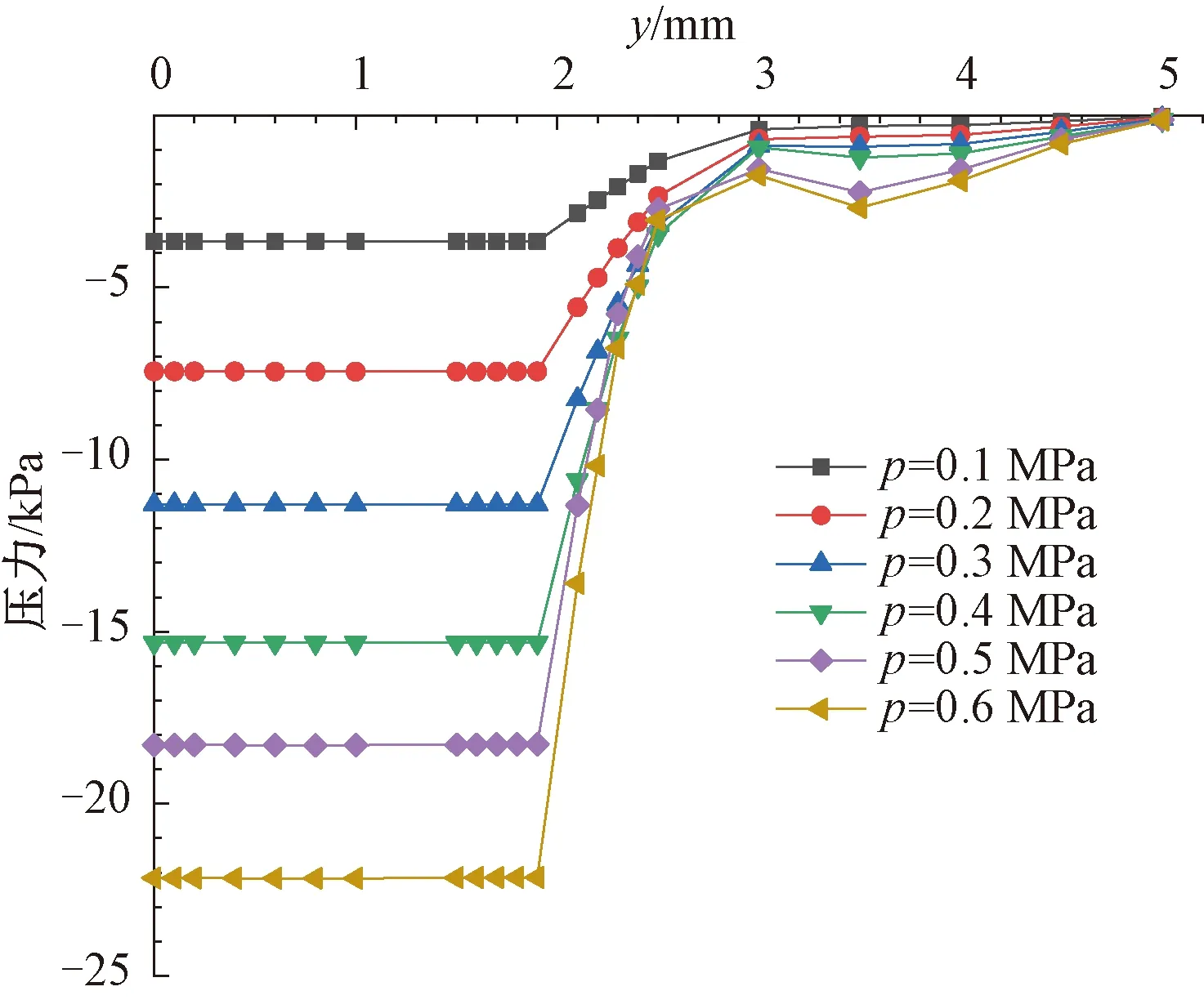
图5 吸附模型中心线沿垂直方向的压力曲线(h=2.0 mm)

3.4.2 间隙区域径向压力分布

当间距h=2.0 mm时不同供气压力下经编鞋面上表面沿径向的压力曲线如图6所示。由图6可知：在x=0～12 mm区域内，压力沿径向几乎没有发生变化；在x=23～30 mm区域内，负压急剧减小并接近于零。

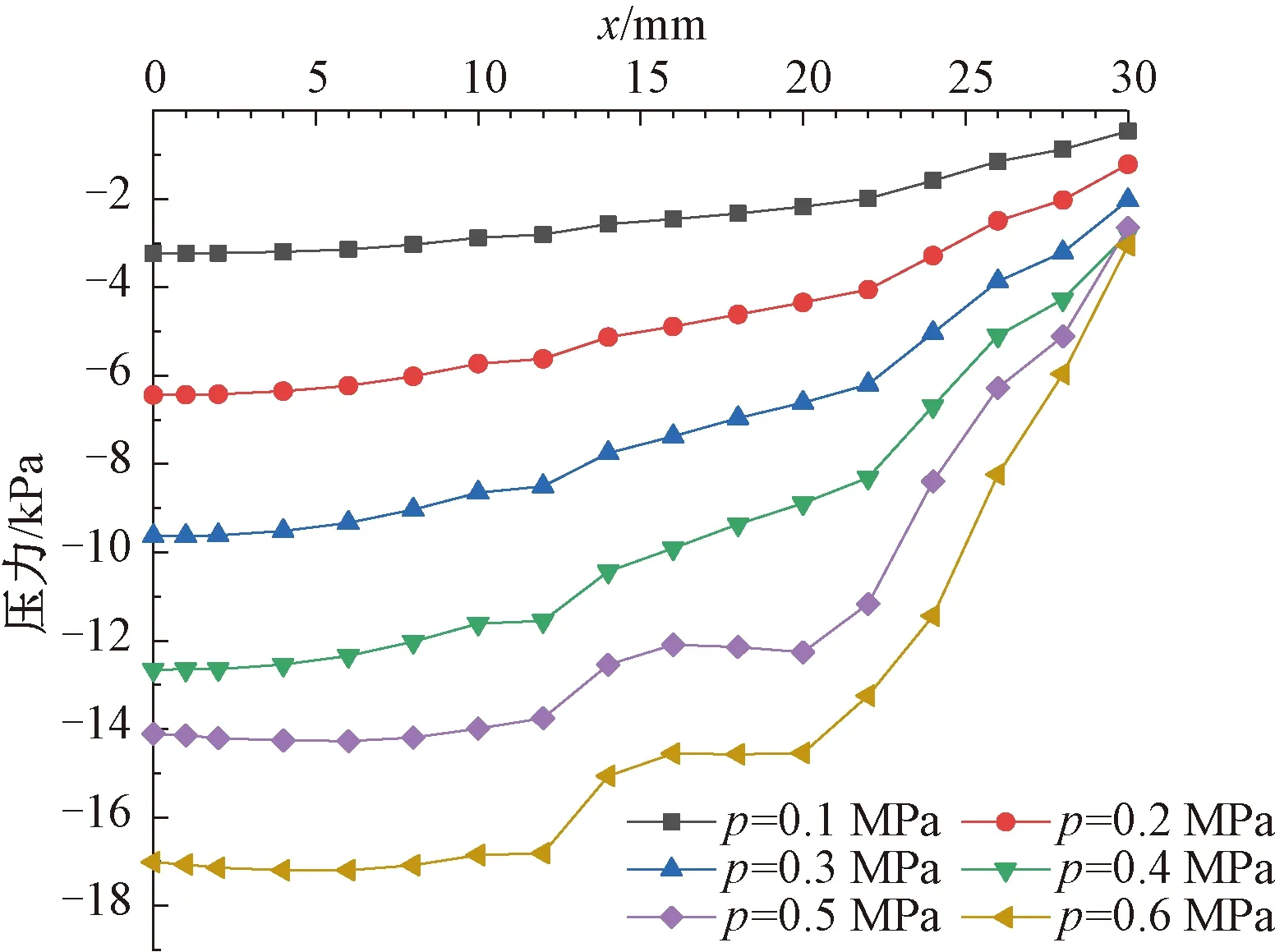
图6 经编鞋面上表面沿径向的压力曲线(h=2.0 mm)

3.4.3 影响吸盘吸附力的因素

(1)吸附力F与供气压力p的关系。不同间距条件下吸附力F与供气压力p的关系曲线如图7所示。由图7可知：当间距h一定时，吸附力F与供气压力p呈正比例关系，与理论分析结果相一致；当间距h≥0.6 mm时，吸附力F数值为正数，表现为吸引力；当间距h=0.4 mm时，吸附力F数值为负数，表现为排斥力。

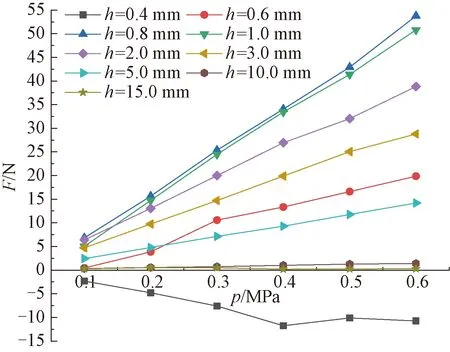
图7 不同间距条件下吸附力F与供气压力p的关系曲线

(2)吸附力F与间距h的关系。不同供气压力下吸附力F与间距h的关系曲线如图8所示。由图8可知：当供气压力p一定时，吸附力F与间距h呈现指数函数关系，与文献[11,14]的研究结果吻合；当间距h≤0.4 mm时，吸附力为负值，随着间距增大，吸附力增大，转变为正值，当吸附力达到最大值后再急剧减小并接近于零。

图8 吸附力F与间距h的关系曲线

4 伯努利吸盘抓取经编鞋面试验研究

为进一步验证本文针对伯努利吸盘抓取经编鞋面稳态过程的数学模型以及数值模拟分析的正确性，研究伯努利吸盘抓取经编鞋面稳态下的最优状态条件，通过试验方法研究各参数对稳定抓取过程的影响。伯努利吸盘抓取经编鞋面试验台如图9所示。

图9 伯努利吸盘抓取经编鞋面试验台

伯努利吸盘抓取经编鞋面试验台主要由机械手、机械手末端执行器(包括伯努利吸盘)、电子天平、调压阀等元器件组成。

首先将经编鞋面平放在电子天平的载物台上，记录电子天平的显示数值(经编鞋面重力G)，然后调节调压阀控制吸盘供气压力，通过控制机械手调节伯努利吸盘与经编鞋面的间距，使得电子天平的显示数值为零，同时经编鞋面与电子天平处于临界分离的静止状态(近似认为经编鞋面处于稳定静止状态)，此时吸附力F等于经编鞋面重力G，记录供气压力p和间距h的数值。当电子天平显示数值大于经编鞋面重力G时，表明此时吸附力F为排斥力；当电子天平显示数值小于经编鞋面重力G时，表明此时吸附力F为吸引力。

当间距h一定时，通过控制经编鞋面重力G和供气压力p，使经编鞋面处于稳定静止状态，得到吸附力F与供气压力p关系的试验曲线如图10所示。当供气压力p=0.6 MPa时，通过控制经编鞋面重力G和间距h，使经编鞋面处于稳定静止状态，得到吸附力F与间距h关系的试验与仿真对比曲线如图11所示。

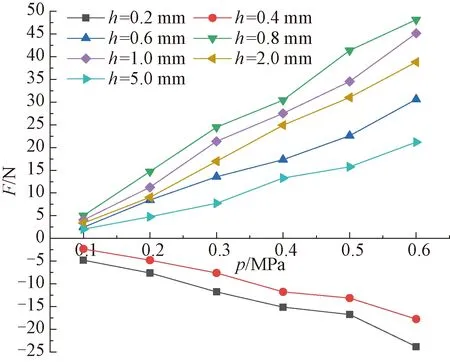
图10 吸附力F与供气压力p关系的试验曲线

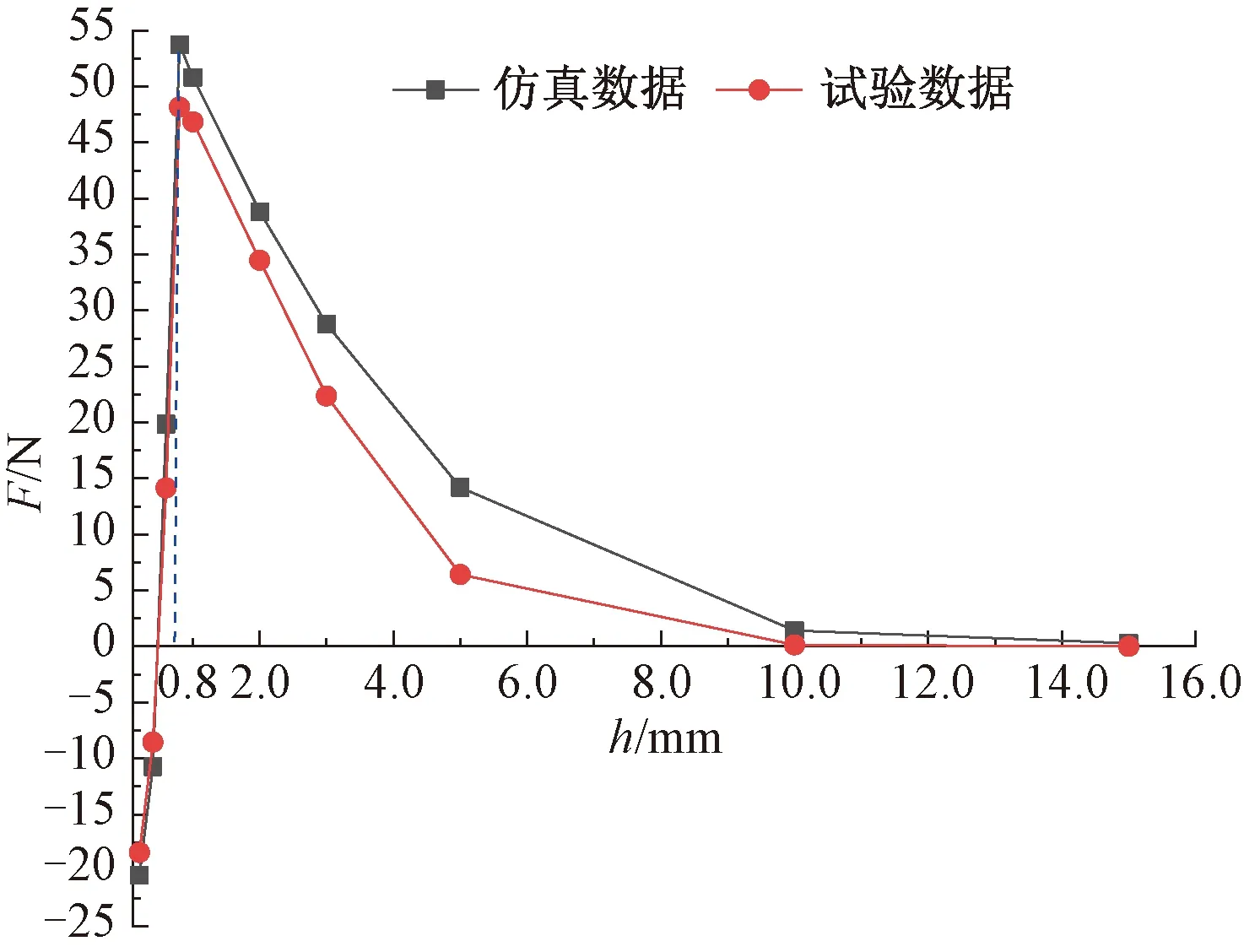
图11 吸附力F与间距h关系的试验与仿真对比曲线(p=0.6 MPa)

由图10可知：在间距h一定时，吸附力F与供气压力p呈正比例关系，与仿真结果相吻合；当供气压力p一定时，间距h=0.8 mm这条曲线所对应的吸附力F均是最大的；当间距h=0.2、0.4 mm时，吸附力数值均为负数，表现为排斥力；当间距0.6 mm≤h≤5.0 mm时，吸附力数值均为正数，表现为吸引力。由图11可知：在供气压力p=0.6 MPa 试验条件下，吸附力F与间距h呈指数函数关系，与仿真结果相符合；当间隙h≤0.4 mm时吸附力表现为排斥力，为负数；随着间距增大，吸附力增大，其数值由负数变为正数，当间距h=0.8 mm 时吸附力F为最大值48 N，随后急剧减小并接近于零。试验结果表明，在确定经编鞋面重力G后，当间距h=0.8 mm、吸附力F=G时，对应的供气压力p即为最优的供气压力。

5 结 论

(1)本文建立了伯努利吸盘抓取经编鞋面稳态过程的数学模型。经数值模拟可知：吸附力F与供气压力p呈正比例关系、与间距h呈指数函数关系；通过对伯努利吸盘抓取经编鞋面稳态过程进行数值模拟分析，得到吸附模型间隙区域的压力分布，验证了数学模型的正确性。

(2)对伯努利吸盘抓取经编鞋面稳态过程进行了试验研究，获得了伯努利吸盘抓取经编鞋面稳态下最优状态的条件，即在确定经编鞋面重力G后，当间距h=0.8 mm、吸附力F=G时，对应的供气压力p为最优供气压力。