伺服驱动系统机械谐振分析及抑制方法研究
2022-03-23王晶晶刘永康谢长贵
王晶晶,陆 宇,刘永康,谢长贵
(1.重庆工程职业技术学院 智能制造与交通学院, 重庆 402260;2.重庆理工大学 车辆工程学院, 重庆 400054)
伺服驱动系统是一种包括驱动电机、传动机构、负载和控制系统的典型复杂机电系统,它可分为机械系统、电气系统和联系二者的耦合磁场3部分。机械谐振的产生是由于系统中传动机构的弹性使得系统本身存在谐振频率,随着伺服驱动系统带宽的增加,当有含谐振频率的信号等作用到系统时,通常会使系统发生机械谐振[1-4]。机械谐振的存在会导致在对伺服驱动系统进行转矩、转速控制时系统发生振荡,当系统长期在机械谐振状态下运行时,不仅会影响系统的控制性能和精度,还可能会损坏传动机构、烧毁驱动电机,甚至引发工业事故[3-5]。因此,对伺服驱动系统机械谐振进行分析和抑制具有重要的实际应用意义,有利于改善工业应用设备的稳定性、安全性和生产效率,同时为研发高性能伺服驱动产品提供理论和实践探索。
国内外学者对于伺服驱动系统的机械谐振抑制方法进行了大量的研究,使用的方法一般可分为主动抑制方法和被动抑制方法2种[6]。主动抑制方法即通过主动改变控制器参数或控制器结构消除机械谐振,包括基于状态观测器的反馈控制、基于模型预测控制(model predictive control,MPC)、基于PI的控制等高级控制算法[3-11]。被动抑制方法主要是使用低通滤波器或陷波滤波器等抑制机械谐振,但低通滤波器会带来相位滞后、陷波滤波器对系统参数变化较敏感,容易导致系统动态性能变差[12-14]。于晶等[9]提出一种高阶滑模与加速度反馈相结合的控制方法,以解决由于伺服驱动系统中传动机构刚度有限带来的机械谐振问题。杨明等[10]提出采用MPC算法代替PI调节器对电机电磁转矩的输出进行预测,实现了轴系转矩的任意限幅,在抑制机械谐振的同时,兼顾了伺服驱动系统的动态响应特性。Szabat等[15]提出基于负载转矩反馈的抑制方法,通过确定最优惯量比计算得到负载转矩反馈系数,将扰动力矩检测出来反馈至电流环给定,从而达到抑制机械谐振的效果。龚文全等[16]使用改进型陷波滤波器进行机械谐振抑制,以减小陷波器引入的相位滞后。
为了研究伺服驱动系统的机械谐振的机理,提高系统的控制品质,首先建立双惯量伺服驱动系统模型,然后从引起机械谐振的原因、机械谐振影响因素2个方面,对双惯量伺服驱动系统机械谐振进行分析,最后采用MPC方法对双惯量伺服驱动系统机械谐振进行抑制,并通过仿真和试验验证MPC控制器的有效性。
1 伺服驱动系统建模
伺服驱动系统在许多工业领域如数控机床、机器人、电动汽车驱动系统、高端试验装备,以及国防工业中应用十分广泛,其转矩传递通常由多个不同的机械传动机构完成。如图1所示为一个典型的伺服驱动系统结构,负载通过联轴器、齿轮箱、传动轴等与驱动电机相连。
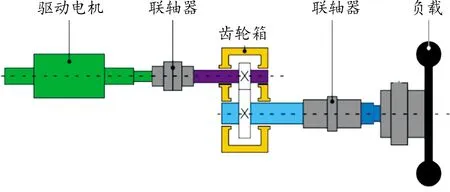
图1 伺服驱动系统结构示意图
为了便于分析,忽略图1中间传动机构的影响,同时忽略电机的电磁阻尼和电磁刚度,将电机、中间传动机构和负载简化为2个集中的转动惯量元件,得到双惯量伺服驱动系统模型,如图2所示。该模型中电机转轴通过弹性轴与负载连接,系统输入为电机端电磁转矩Te直接作用于电机转轴,传递转矩Ts与负载转矩TL共同作用决定负载端输出转速。
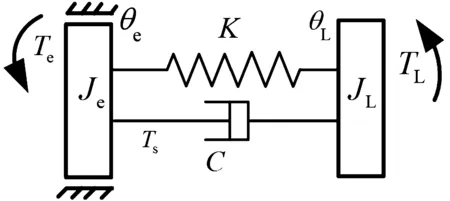
图2 双惯量伺服驱动系统模型示意图
图2所示的双惯量伺服驱动系统的动力学方程可以表示为[6]:
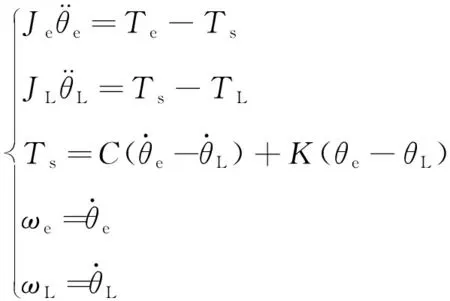
(1)
式中:θe、θL分别为等效电机轴和负载的转角;Je、JL分别为电机和负载的转动惯量;C为传动轴的阻尼系数;K为传动轴的刚度系数;ωe、ωL分别为电机转速和负载转速。
由式(1)可以得到双惯量伺服驱动系统结构框图,如图3。
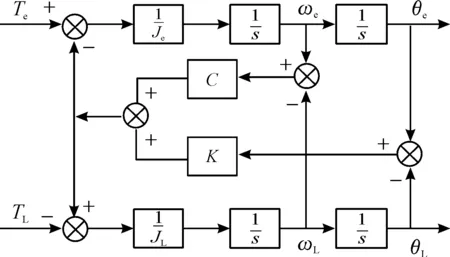
图3 双惯量伺服驱动系统结构框图
因此,根据式(1)和图3,可以写出双惯量伺服驱动系统电机转速和负载转速到电磁转矩的传递函数为[6]:
(2)
(3)
为了对双惯量伺服驱动系统机械谐振进行分析,选取系统参数如表1所示。

表1 双惯量伺服驱动系统参数
2 伺服驱动系统机械谐振分析
2.1 伺服驱动系统的机械谐振产生原因
在双惯量伺服驱动系统中,中间轴的弹性使其自身存在一定的谐振频率,谐振频率的存在会给系统带来机械谐振[17]。进一步从理论上分析机械谐振产生的原因,首先对式(2)(3)电机转速、负载转速到电磁转矩的传递函数进行分析,可知传递函数中包括惯性环节和二阶振荡环节,惯性环节代表了系统的刚性连接部分,二阶振荡环节代表了系统的弹性连接部分。令G(1)为惯性环节,G(2)为二阶振荡环节,其表达式为[5]:
(4)
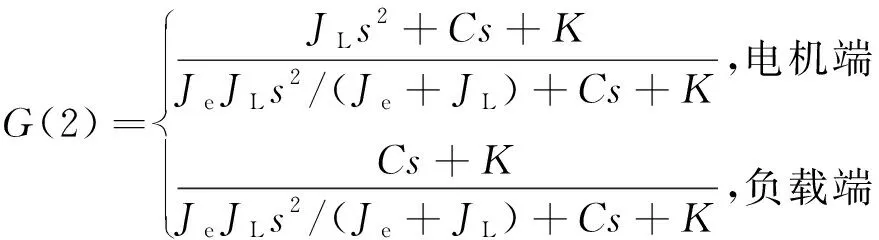
(5)
对式(5)可以进一步表示为:
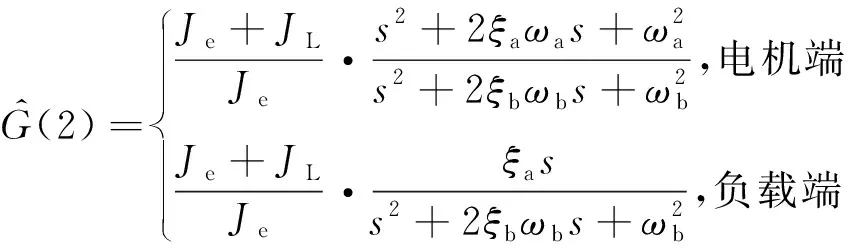
(6)
式中:ωb和ωa分别为系统的谐振频率和反谐振频率;ξb和ξa分别为系统的谐振阻尼系数和反谐振阻尼系数。
低频段由于s较小,二阶振荡环节约为1,即系统的传递函数可以简化为G(1),这时可以把系统看成刚性连接;而中高频段系统的状态由二阶振荡环节的分子和分母共同决定,s平面存在共轭零极点,共轭零极点的存在是导致系统产生机械谐振的根本原因。当考虑电机端转速反馈时的传递函数时,假设式(5)中的分子、分母分别为零,可以解得双惯量伺服驱动系统的共轭零点(即反谐振点)、共轭极点(即谐振点),其表达式为[2]:
(7)
(8)
然后由式(1)可以得到所建立的双惯量伺服驱动系统中输入量电磁转矩到输出量电机转速的波特图,如图4所示。从图4中幅值图可以看出,系统存在一对谐振点和反谐振点,即系统中传动轴会给系统带来共轭零极点,使得系统产生机械谐振。同时由图4中相位图也可以看出,在谐振幅值附近,系统开环增益上升到0 dB以上,此时与系统相位穿越频率重叠,根据经典控制理论的稳定性判断,系统不稳定,会产生谐振现象。
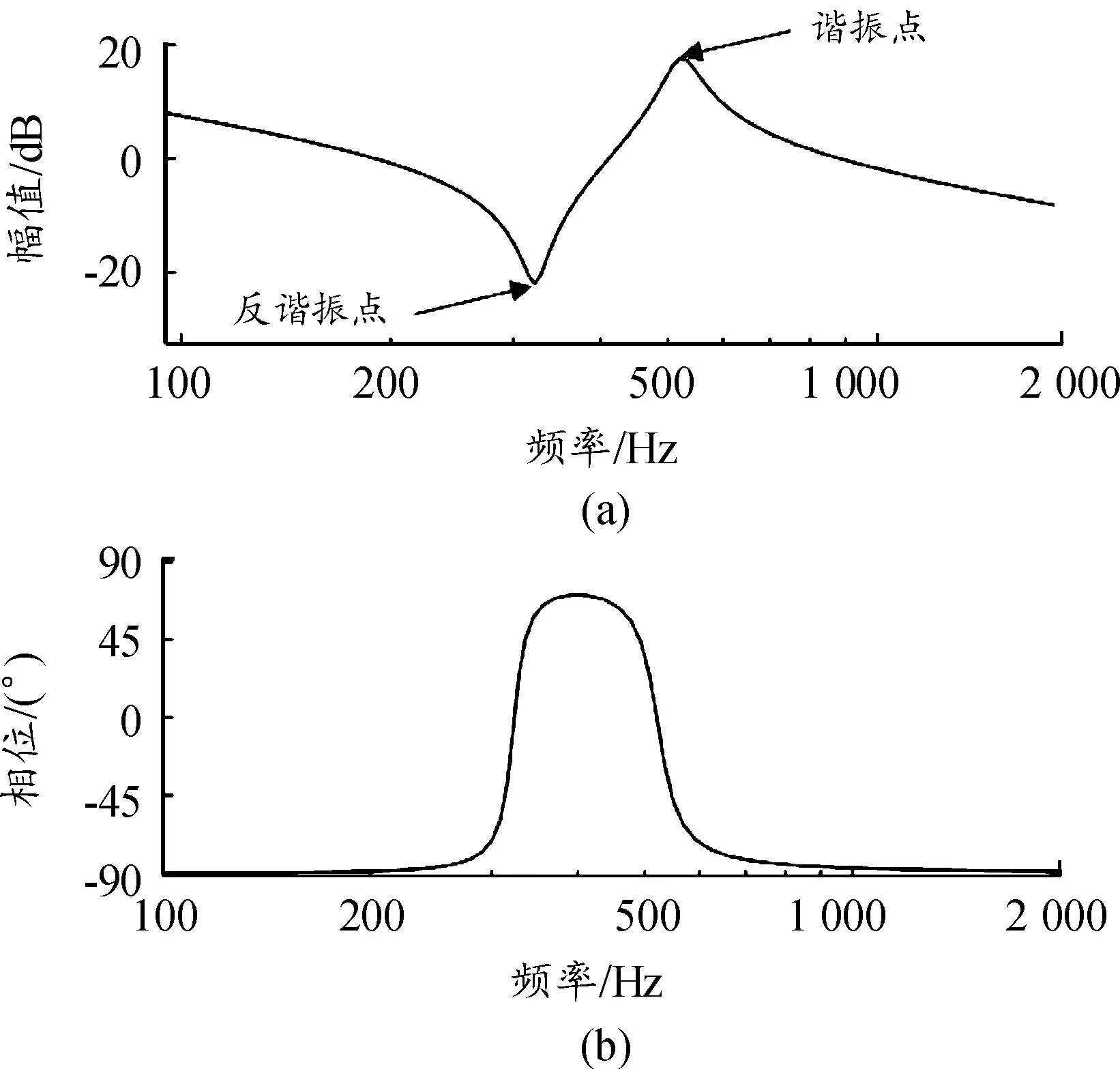
图4 电机端转速反馈时波特图
2.2 伺服驱动系统的机械谐振影响因素分析
由2.1节分析可知,系统机械谐振频率与电机、负载的转动惯量和传动轴的刚度系数有关,同时考虑传动轴阻尼系数可能对谐振的影响,本节选取惯量比、传动轴刚度系数和传动轴阻尼系数3个指标,分析双惯量伺服驱动系统的机械谐振,其中惯量比RI的定义为负载惯量比上电机惯量[18],即:
(9)
传动轴的扭转阻尼主要为材料阻尼,根据李润方等的研究,传动轴的阻尼系数可以表示为[19]:
(10)
式中:ξs为阻尼比,一般为0.005~0.075。
2.2.1不同惯量比对机械谐振影响分析
假设双惯量伺服驱动系统的惯量比取值如表2所示,系统其余参数不变,可以得到如图5所示的不同惯量比下负载端转速到电磁转矩的波特图。从图5中分析可知,惯量比的改变会影响系统的谐振频率,随着惯量比的增大,系统谐振频率会相应减小。
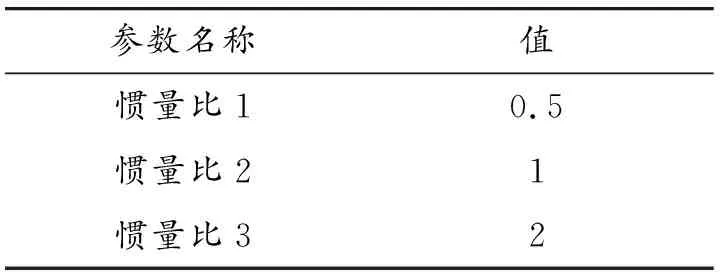
表2 双惯量伺服驱动系统惯量比
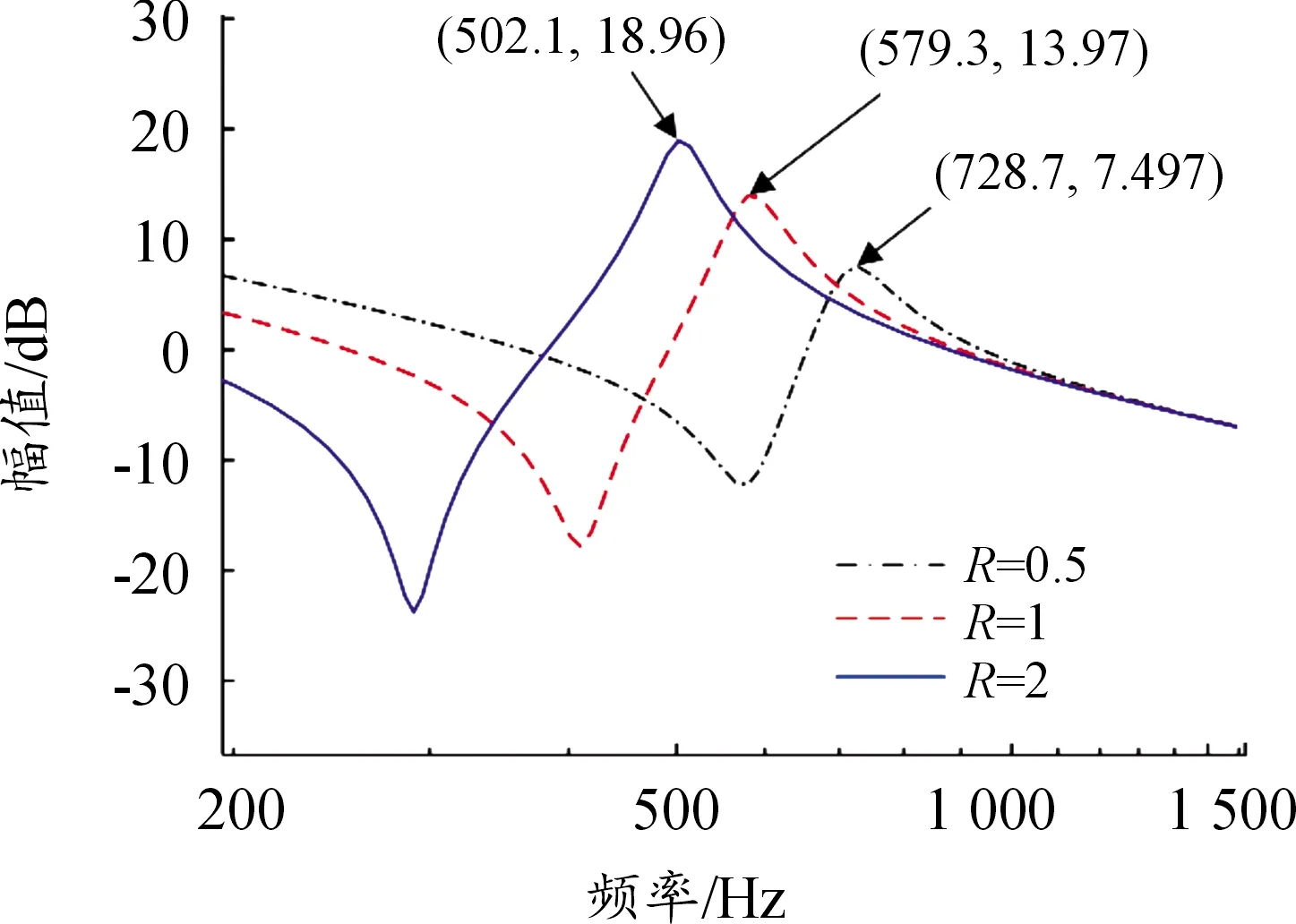
图5 不同惯量比下电机端转速反馈时的波特图
2.2.2不同传动轴刚度系数对机械谐振影响分析
双惯量伺服驱动系统中,传动轴刚度系数是分析系统机械谐振不可或缺的一个重要因素。这里假设双惯量伺服驱动系统按表3所示的值对传动轴刚度系数进行取值,且不改变系统其余参数,可以得到如图6所示的、不同传动轴刚度系数下负载端转速到电磁转矩的波特图。由图6可知,传动轴刚度系数的变化会使得系统的谐振频率发生改变,系统谐振频率随着传动轴刚度系数的增加而增加。

表3 双惯量伺服驱动系统传动轴刚度系数
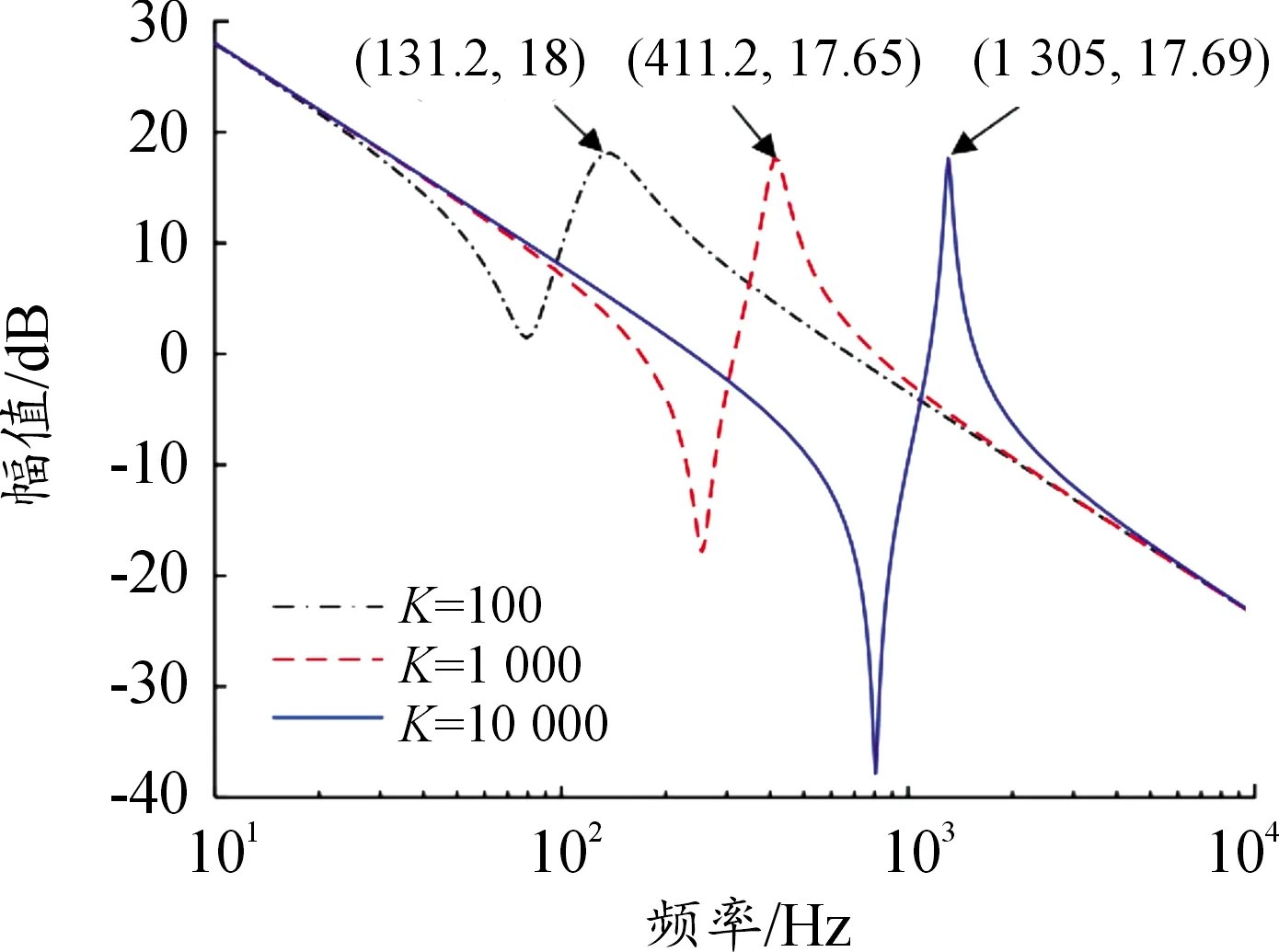
图6 不同传动轴刚度系数下电机端转速反馈时的波特图
2.2.3不同传动轴阻尼系数对机械谐振影响分析
第四,数据库的事务管理与运行管理功能。该功能特指在建立、运用与维护数据库的同时对数据库管理系统进行统一管理和控制,以此确保数据的安全性、完整性与多用户并发使用性以及发生故障后的系统恢复性。
最后,分析传动轴阻尼系数对系统机械谐振的影响。假设传动轴阻尼系数分别取3个不同的值,如表4所示,同时系统其余参数不变,可以得到如图7所示的、不同传动轴阻尼系数下负载端转速反馈时的波特图。对图7进行分析可知,传动轴阻尼系数的变化对系统谐振频率影响不大,但随着阻尼系数的增加,谐振频率的谐振峰值会明显下降。一般来说,弹性传动轴阻尼系数较小,因此,目前大多数对机械谐振抑制方法进行研究时都忽略了传动轴的阻尼。
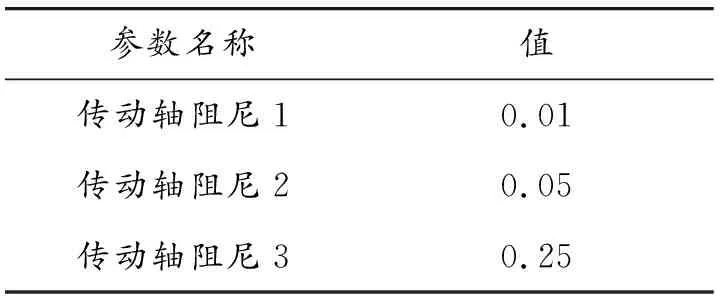
表4 双惯量伺服驱动系统传动轴阻尼系数
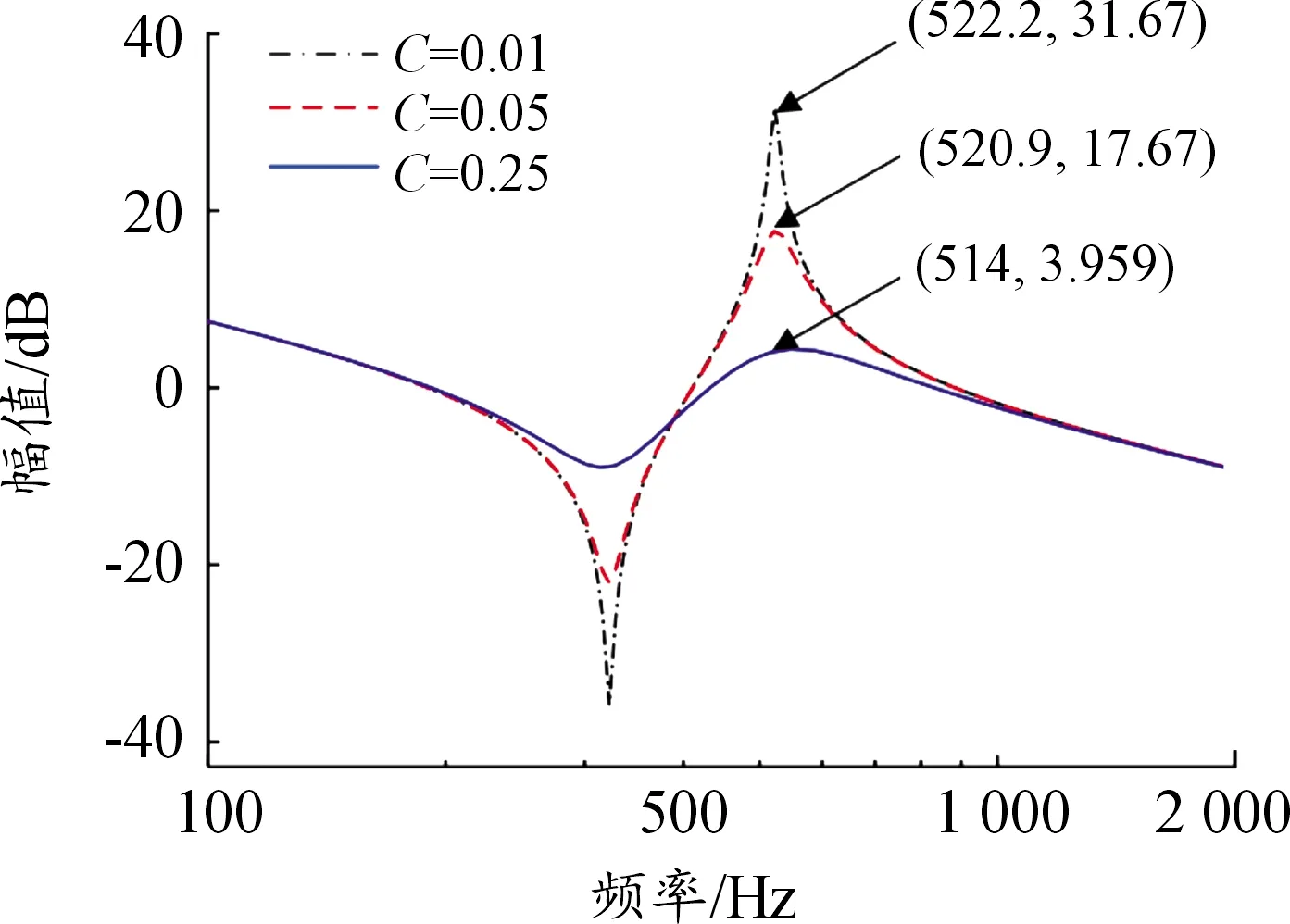
图7 不同传动轴阻尼系数下电机端转速反馈时的波特图
3 基于MPC伺服驱动系统机械谐振抑制方法
MPC方法基本原理是根据系统的预测模型、当前时刻的状态和未来的控制量预测系统未来一段时域的输出,通过滚动求解满足目标函数和各种约束的优化问题,得到系统实际控制输入量,从而实现控制目的[20]。为了对双惯量伺服驱动系统机械谐振进行抑制,基于MPC方法获得系统控制输入量Te,控制的目标是有效地抑制系统的机械谐振,同时使系统具有良好的动态性能,即系统输出转速能很好地跟踪其参考值。图8为伺服驱动系统MPC控制框图,伺服驱动系统处于速度控制模式。
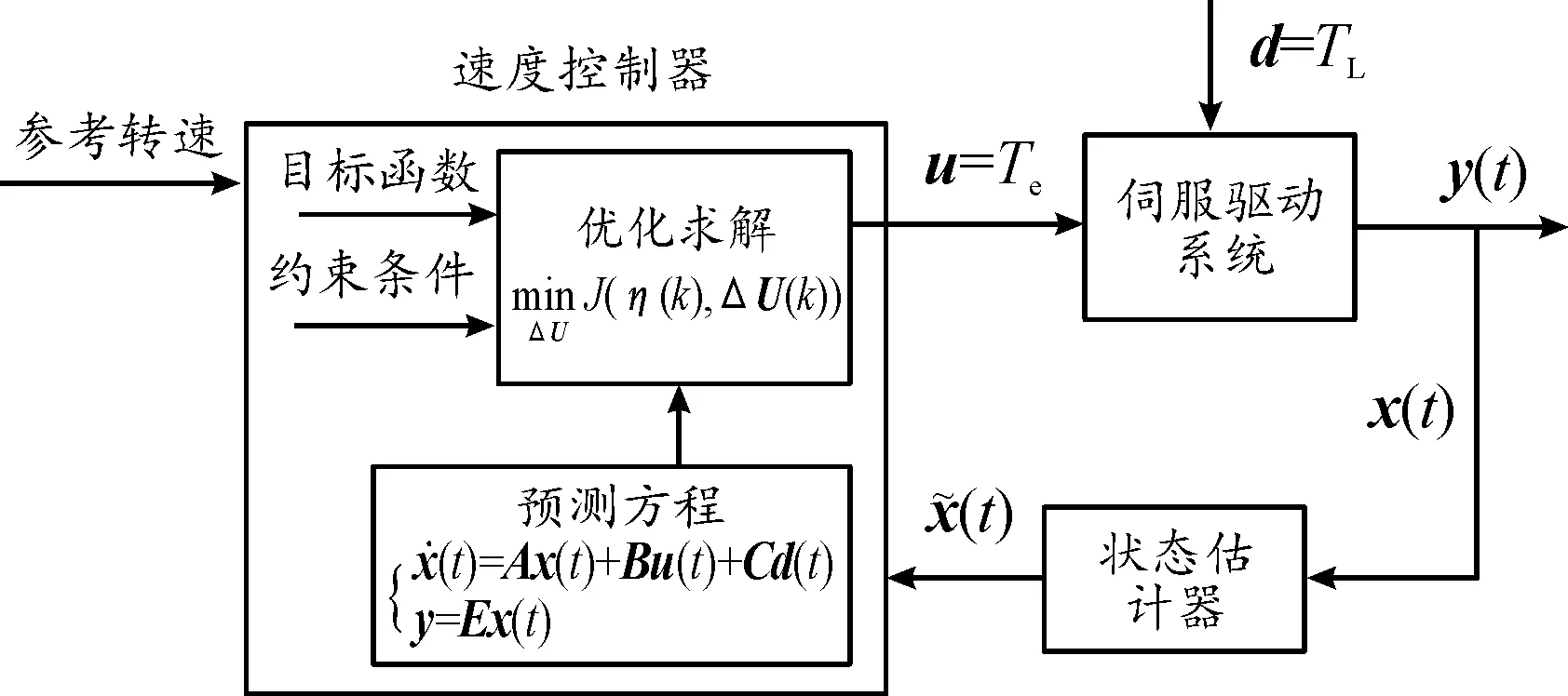
图8 伺服驱动系统MPC控制框图
3.1 预测模型建立
由式(1)可以得到双惯量伺服驱动系统的连续系统状态空间方程[10]:
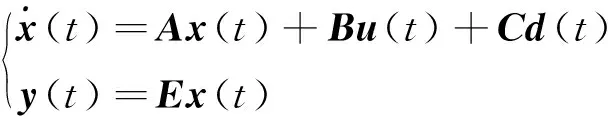
(11)
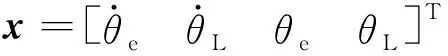
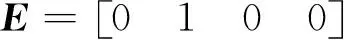
使用前向欧拉法对式(11)进行离散化处理,得到离散系统的状态空间方程如下:

(12)
式中:k为当前采样时刻,k+1为下一个采样时刻。
3.2 目标函数设计
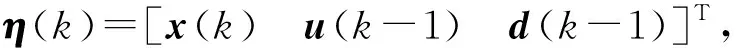
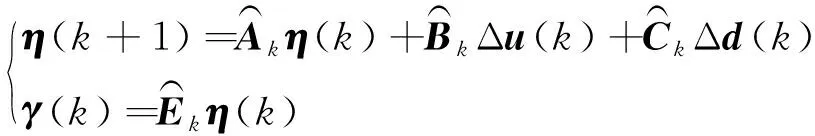
(13)
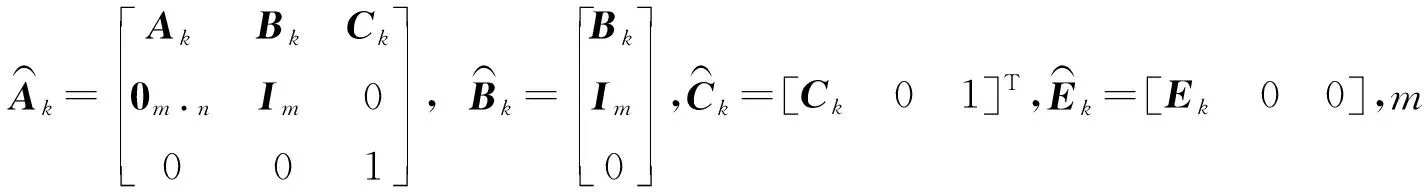
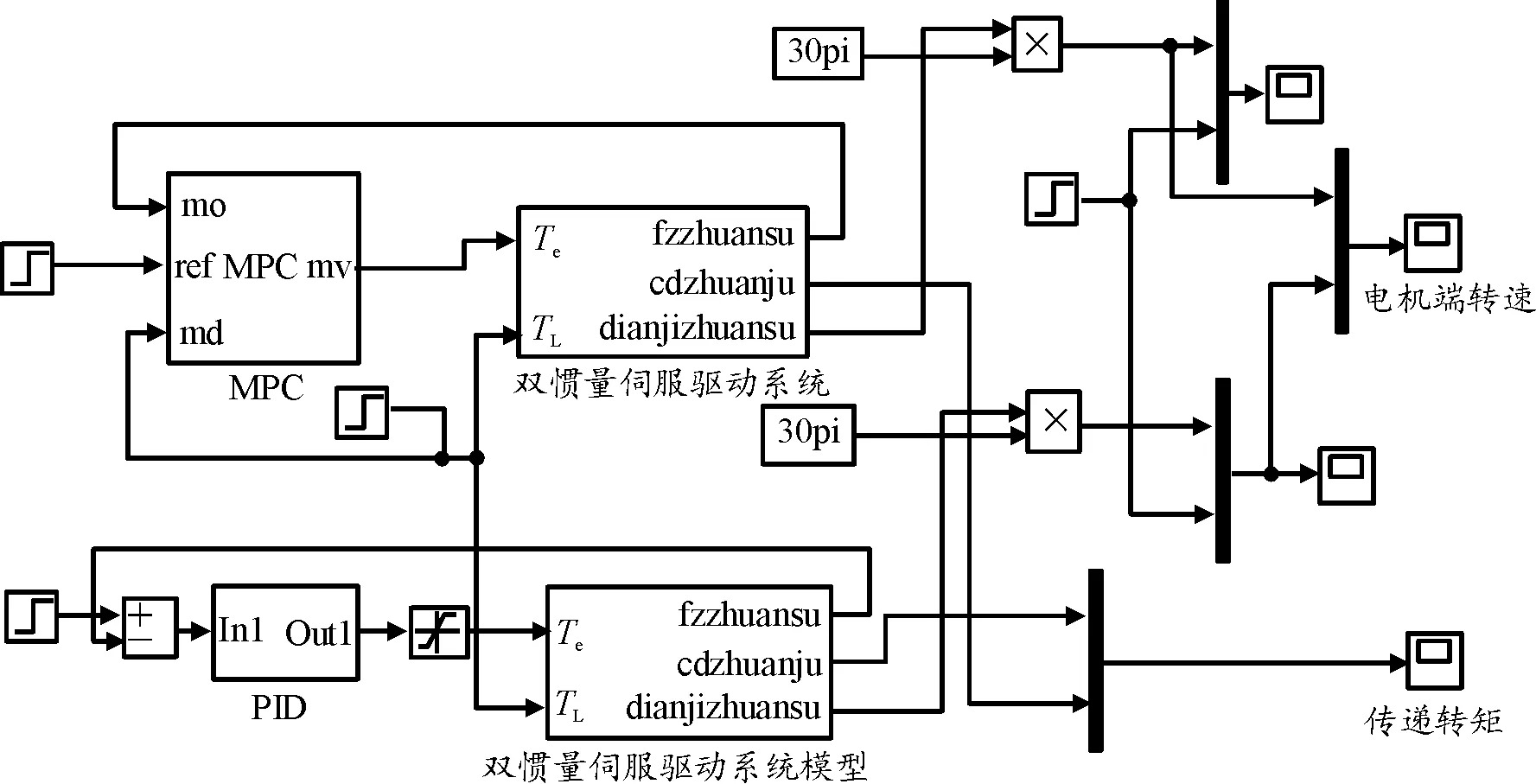
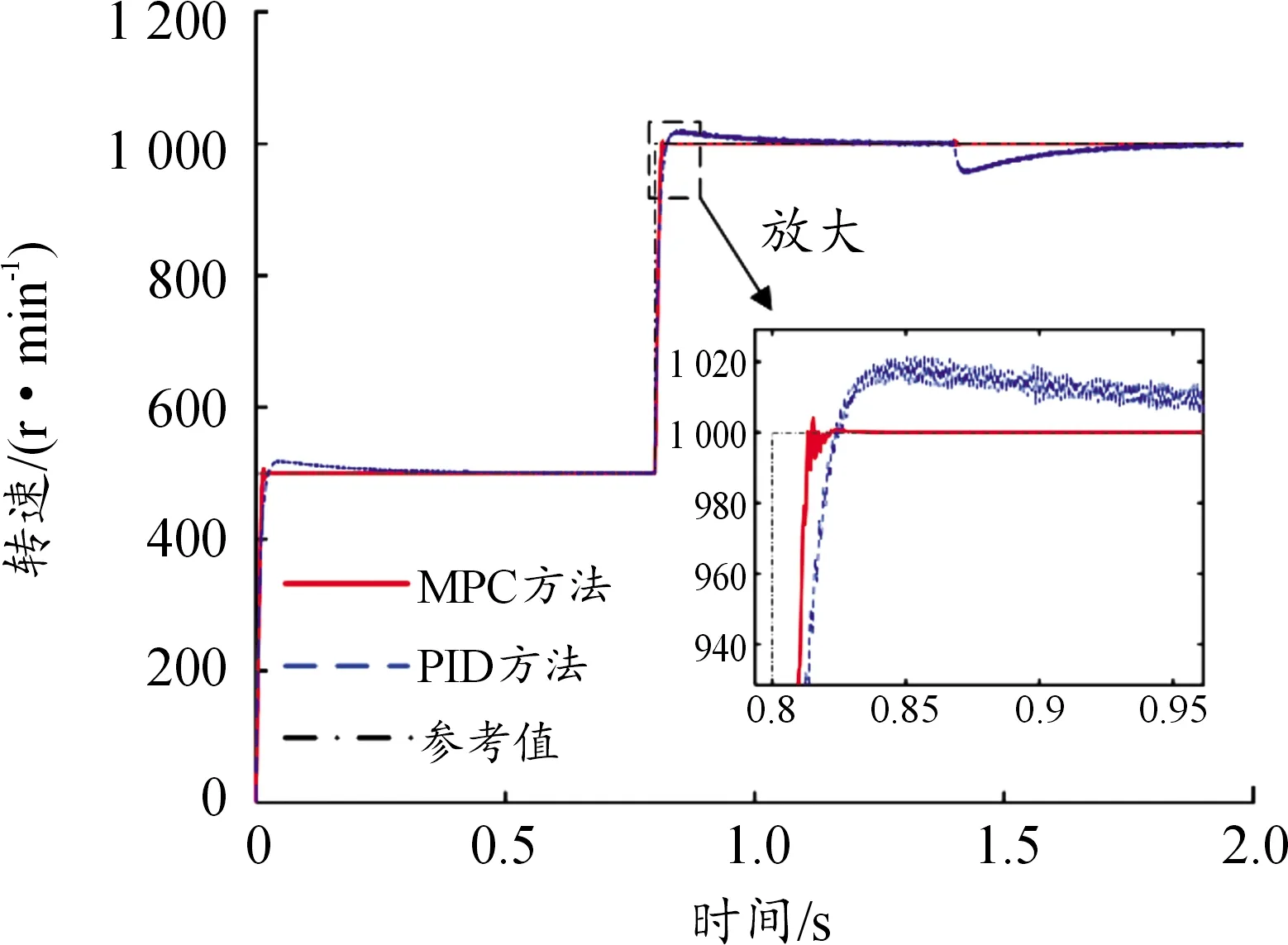
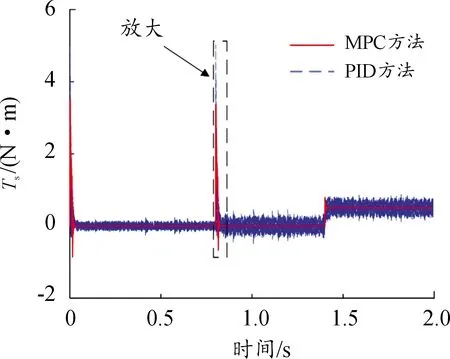
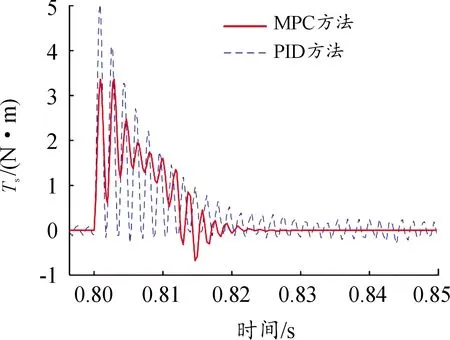
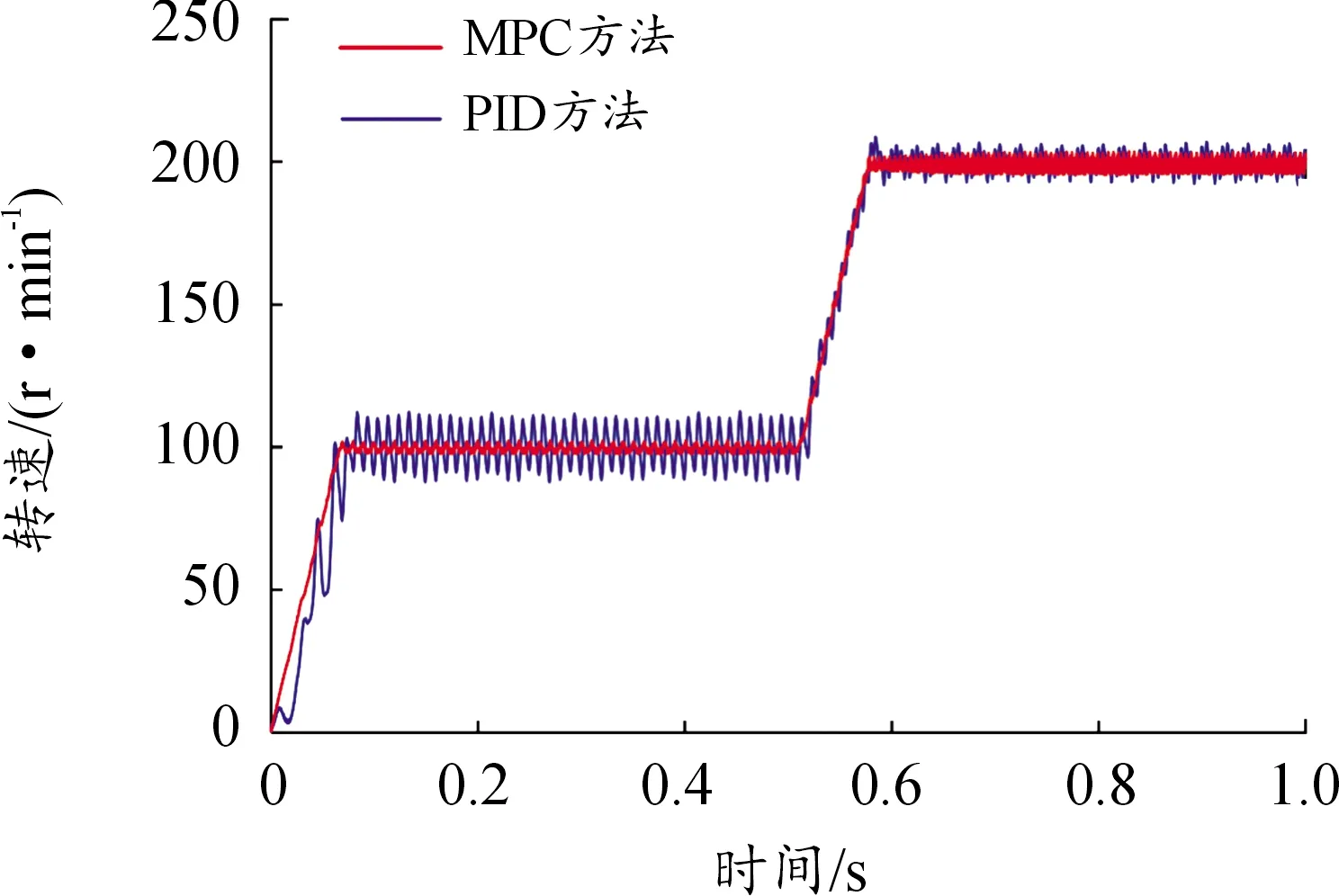
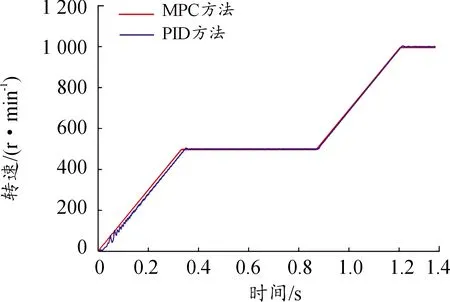
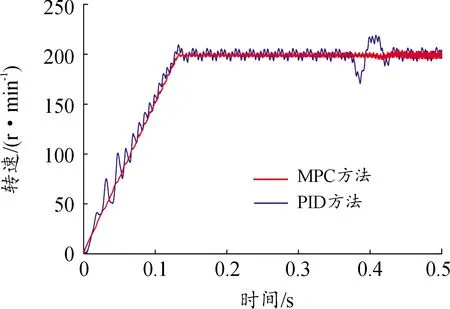
设定预测时域为Np,控制时域为Nc,Nc Y(k)=Φη(k)+ΨΔU+ΓΔD (14) 式中, 考虑系统控制目标为在不超过最大允许电磁转矩的前提下实现转速的精确跟踪,设计优化目标函数为: (15) 式中:Yref(k+i|k)为系统输出变量的参考值,(k+i|k)表示以k时刻的系统输出量来预测k+i时刻的值,其中i=1,2,…,Np;ΔU(k+i)为k+i时刻系统控制输入增量,即电磁转矩增量,其中i=0,1,…,Nc-1;Q和R为权重矩阵。 系统需要对控制输入的电磁转矩、电磁转矩增量及系统输出施加约束条件,控制输入及其增量约束条件为: (16) 式中:umin和umax分别为电磁转矩的最小值和最大值;Δumin和Δumax分别为电磁转矩增量的最小值和最大值。 系统输出约束条件为: γmin≤γ(k+i)≤γmax (17) 式中:γmin和γmax分别为系统输出的最小值和最大值。 系统优化求解问题即在预测时域里,式(15)在满足式(16)(17)的约束条件下达到最小。即在每个控制周期里需要解决以下问题: (18) 式中:Umin和Umax分别为控制量的最小值集合和最大值集合;ΔUmin和ΔUmax分别为控制增量的最小值集合和最大值集合;S=K⊗Im;Ut=1Nc⊗u(k-1),1Nc为Nc行的列向量,u(k-1)为k-1时刻的实际控制量,⊗为克罗内克积; 通过求解二次规划问题,可以得到控制时域内的系统控制输入增量为: (19) 将控制输入增量的第一项Δu(k)取出,即可得到当前时刻系统控制输入为: u(k)=u(k-1)+Δu(k) (20) 为了验证MPC方法对双惯量伺服驱动系统的机械谐振抑制的有效性,并与基于PID方法的控制效果进行比较,在Matlab/Simulink中建立了系统仿真模型,如图9所示。伺服驱动系统主要参数如表1所示。 图9 伺服驱动系统仿真模型示意图 MPC控制器主要参数设为:预测时域Np=10,控制时域Nc=3,权重取值Q=0.5、R=1,系统控制输入的电磁转矩范围|Te|≤5 N·m,系统输出的转速范围|γ|≤18 000/π r/min;PID控制器参数设为:比例系数0.1,积分系数0.6,微分系数0.000 1。 当给定参考转速0~500~1 000 r/min,且在1.4 s加入0.5 N·m的负载扭矩时,图10为电机端转速变化的仿真结果,由图10可知,MPC方法下,转速的响应时间和超调量均优于PID方法,其中MPC控制下的超调量约为0.5%、PID控制下的超调量约为2%。对系统加入负载扭矩干扰后,MPC方法下转速能够快速调节至参考转速,这说明其抗干扰能力好。图11、12为传递转矩Ts的变化曲线,由图可知,在电机启动、加速及负载转矩突变时,中间传递转矩都产生了较大的振荡,使用PID方法时,传递转矩的振荡总体上大于MPC方法时。仿真结果说明,使用MPC方法抑制机械谐振有效且达到了预期控制效果。 图10 MPC和PID方法下转速阶跃响应时电机端转速曲线 图11 MPC和PID方法下转速阶跃响应时传递转矩Ts变化曲线 图12 MPC和PID方法下转速阶跃响应时传递转矩Ts变化曲线(局部放大图) 为了进一步验证MPC方法抑制伺服驱动系统机械谐振的有效性,利用如图13所示的试验台进行了基本的试验。试验台架选取永磁同步电机作为伺服驱动系统的执行机构,完整的台架系统包括驱动电机、电机驱动器、联轴器、转矩转速传感器、磁粉制动器、直流电源、上位机及控制软件等。其中驱动电机的额定功率为750 W,额定转矩为2.4 N·m,转动惯量为2.4×10-4kg·m2;联轴器的刚度为1 600 N·m/rad。 图13 伺服驱动系统试验台 当给定参考转速为0~100~200 r/min,负载扭矩为0时,图14为转速阶跃响应时电机端转速试验结果。 图14 MPC和PID方法下电机端转速曲线(0~100~200r/min) 由图14可知,与PID方法下的转速试验结果相比,MPC方法下的转速超调量更小;且PID方法下转速会产生较大的振荡,在100 r/min稳态阶段的振荡范围为87~111 r/min,利用MPC方法能有效的减小系统的振荡,在100 r/min稳态阶段的振荡范围为98~102 r/min,这和仿真试验结果的结论基本一致,说明MPC方法抑制机械谐振的有效性。图15为给定参考转速为0~500~1 000 r/min,负载扭矩为0时电机端转速试验结果,从图15可以看出,MPC方法下的响应时间优于PID方法,电机启动阶段PID方法的转速振荡较大,说明PID方法动态性能较差。 图15 MPC和PID方法下电机端转速曲线(0~500~1 000 r/min) 为了验证MPC方法下系统的抗干扰能力,并与PID控制方法进行对比,给定参考转速200 r/min,当电机转速进入稳态工况后,使用磁粉制动器突加0.5 N·m的负载扭矩,如图16所示为突加负载时电机端转速试验结果。由图16可知,突加负载后,PID方法下电机转速振荡较大,而MPC方法下电机转速波动较小,抗干扰能力优于PID方法,这与仿真试验得到的结论一致。 图16 MPC和PID方法下突加负载时电机端转速曲线 1) 简化典型伺服驱动系统结构,建立了包含电机和负载的双惯量伺服驱动系统模型;从机械谐振产生原因和机械谐振影响因素2个方面,对双惯量伺服驱动系统的机械谐振进行分析,由分析结果可知,相比于系统传动轴阻尼系数,惯量比和传动轴刚度系数对双惯量伺服驱动系统机械谐振影响更为显著。 2) 基于双惯量伺服驱动系统模型设计了模型预测控制器,并与PID方法的控制性能进行了对比;仿真和试验结果表明,MPC方法能有效抑制系统机械谐振的影响,其控制效果优于PID方法。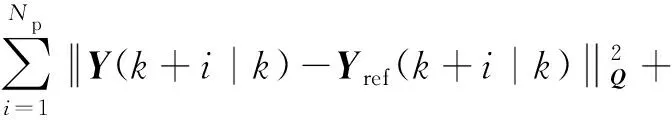
3.3 约束条件设计
3.4 优化求解
3.5 仿真及结果分析
4 试验与结果分析

5 结论
