基于自适应模糊PID 的二级倒立摆控制方法

常昊天，李小兵，钟伟杰

（1.空军工程大学研究生院，西安 710051；2.空军工程大学防空反导学院，西安 710051）

0 引言

二阶倒立摆是强非线性、高阶次、不稳定系统，必须采取有效控制算法才能使之稳定。倒立摆在军工、航天、通信、机器人、机械制造等领域中都有着广泛的用途和开发前景。

进入21 世纪后，二级倒立摆的研究主要汇集在两个方向：一是如何准确、快速地从起始位置到达预设位置的起摆控制。现阶段应用能量反馈方法基本能够快速准确完成此类控制。二是倒立摆临近平衡点的稳定控制。近些年来，国内外很多学者都针对平衡点附近的稳定控制展开了大量研究工作。对于一级倒立摆系统，诸如极点配置、状态反馈控制、鲁棒控制等现代控制方法已能够较好地契合和解决，但这类方法对于二级倒立摆这样的强非线性且不稳定的系统，控制效果则往往不理想。

目前，针对二级倒立摆的控制方法，如文献［5-6］提出了根轨迹、PID 等经典控制理论方法。文献［8］提出了一类模糊逻辑与神经网络结合的方法，能够有效控制非线性系统。但是这些控制方法过度依赖人为的经验，无法及时应对突发故障，控制效果泛化性不高。文献［9］应用LQR 方法对倒立摆进行线性二次型最优控制，但该方法仅能维持控制系统在平衡点附近达到小范围局部最优，外界一旦出现干扰信号，便会出现小车跟随能力下降的情况。文献［10-12］提出了H控制、滑膜变结构控制、拟人控制等现代控制方法，控制精度高且能使二阶倒立摆实现大范围渐进稳定，但是这类控制方法大多较为复杂，控制过程的延迟时间较长，对二级倒立摆进行实时控制的效果不佳。

若要在大范围内既实现对二阶倒立摆的稳定控制，又降低随机扰动对系统的影响，且具有快速性。设计一种性能更优的控制器，不断提升系统的抗扰能力，仍是当前国内外学者在此方面关注的问题。

1 二阶倒立摆的模型建立

二级倒立摆的平面示意图如图1 所示，忽略空气流动和摩擦等微小因素，倒立摆系统可以描述为由小车、传送带、均匀材质摆杆和质量块组成的系统。

图1 二级倒立摆示意图

对小车、摆杆、传送带进行受力分析后，采用分析力学中的Lagrange 方程和能量守恒定律，易推导建立二级倒立摆的运动学微分方程式：

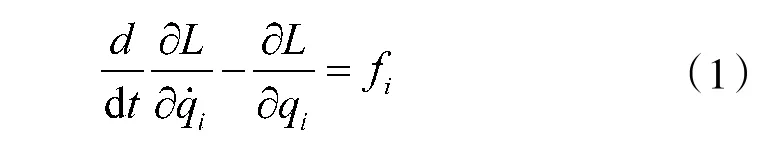
其中，为Lagrange 算子，表示系统具有的能量，为系统的广义坐标，为系统具有的动能，定义为：

其中，T为小车的动能，T、T为摆杆的动能。通过对小车受力分析，在水平面小车所受合外力为皮带的摩擦阻力。再对摆杆受力分析，将其所受重力与支持力代入到微分方程便得到式（3）：

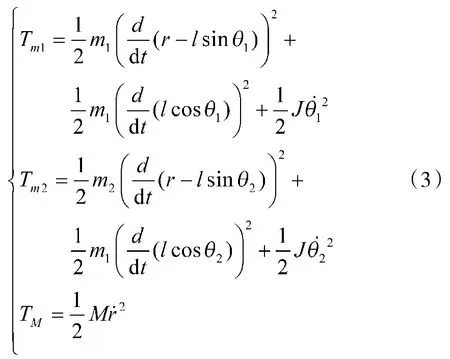
为系统具有的势能，定义为式（4）：

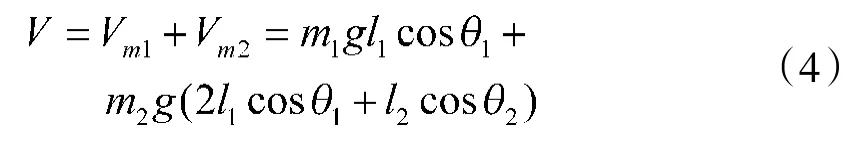
考虑到二级倒立摆系统的控制最终目的是平衡，因此，在建模时可以对摆杆的上、下摆角在平衡点附近进行线性化。当摆杆角度足够小时，认为系统达到了平衡点。动态方程式可进行线性化处理，即：

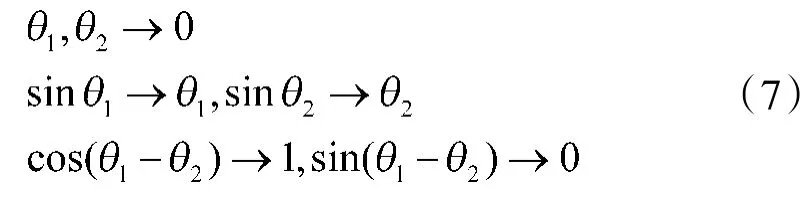
则，得到系统的状态方程：

其中，状态向量为：

2 二级倒立摆模糊PID 控制

2.1 模糊PID 控制器结构

由于二级倒立摆非线性特性，对倒立摆单独使用PID 控制，系统的稳定性、鲁棒性较差。对倒立摆单独使用模糊控制，则可能存在因人为经验不足使模糊规则数不够，引起控制精度会不理想。因此，结合PID 控制的广泛性、适用性与模糊控制的智能性、简化系统设计的复杂性，设计一种自适应模糊PID 控制器。即在无需预先整定PID 参数的情况下，实现对二级倒立摆的多状态量的稳定控制。以下，主要考虑对小车的位移，下摆杆与垂直面的夹角和上摆杆与垂直、面的夹角这3 个参量的控制。

2.2 PID 参数的自校正整定

PID 控制器在离散域内的控制算法定义为式（9）：

图2 模糊PID 控制原理图

式中，k、k、k分别为比例、积分、微分的作用系数（），（-1）为当前时刻和上一时刻期望输出与真实输出的偏差。目前，工业过程控制中最广泛的应用仍是PID 算法，或是以其思想为基础的改进算法。其控制精度的高低直接取决于控制对象模型所辨识程度的好坏。且在控制过程中对于如何整定PID 控制器的参数也具有很大的工作量，往往需要操作人员根据实际的经验知识进行整定。这对于复杂、高阶次、不稳定的系统是十分困难的，因此，需要根据现场实际情况，设计一种方法使计算机能够实时校正PID 控制器的参数。

PID 控制器的在线校正方法如式（10），K为误差量化因子，K为误差变化率量化因子，K为输出控制量比例因子。作为模糊控制器输入输出的比例系数，量化因子和比例因子反映了模糊论域与实际范围之间的比例关系。K、K、K为原始量，ΔK、ΔK、ΔK为PID 控制器的调整量。

2.3 模糊规则的制定

模糊控制器采取两输入三输出的形式，将小车位移、上摆角、下摆角与期望输出偏差值定义为误差，将误差以及误差对时间的变化率C进行模糊推理后作为控制器的两个输入量，PID 控制器的校正量ΔK、ΔK、ΔK作为3 个输出量。模糊控制器5 个变量的模糊子集设为{，，，，，，}含义为{负大，负中，负小，零，正小，正中，正大}。文献［15］提出了一种设计模糊PID 控制器模糊论域及基本论域参数确定的思路。

据此，需要制定K、K、K这3 个参数整定的模糊规则，模糊控制器中包含7 个模糊子集，因此，PID 的每一个参数整定需要编写49 条模糊规则。

误差以及误差对时间的变化率的比值为负时，上升阶段会产生一定超调量。积分环节出现超饱和的现象，此时应设置K较大，加大比例环节作用；设置K较小，减弱积分环节，并取一定数值的K防止超调量过高，利用比例环节回调曲线。K、K、K的参数整定规则如下：

误差以及误差对时间的变化率C的比值为正时，出现两种情况：一是输出未达到设定值便偏离设定值。此时调高积分系数K，比例系数K，目的为增大输出量。二是出现超调量后，输出值第2 次未达到设定值，相比于第1 次，输出量偏离设定值较小，此时，需要增大积分环节系数K比增加比例环节系数K后出现超调量的概率小，K取适中数值。

误差以及误差对时间的变化率C的比值取值接近零时，应设置K和K均取较大值，保持系统的运行平稳。同时设置K取较小值，防止系统出现震荡。

考虑到高斯型函数灵敏度较高，且函数曲线相对平滑，并可以在论域范围内均匀分布，故将其作为隶属度函数。系统根据反馈跟踪与C的不同数值，调整ΔK、ΔK、ΔK，得到PID 控制规则，并建立表1 关于ΔK、ΔK、ΔK控制规则表。

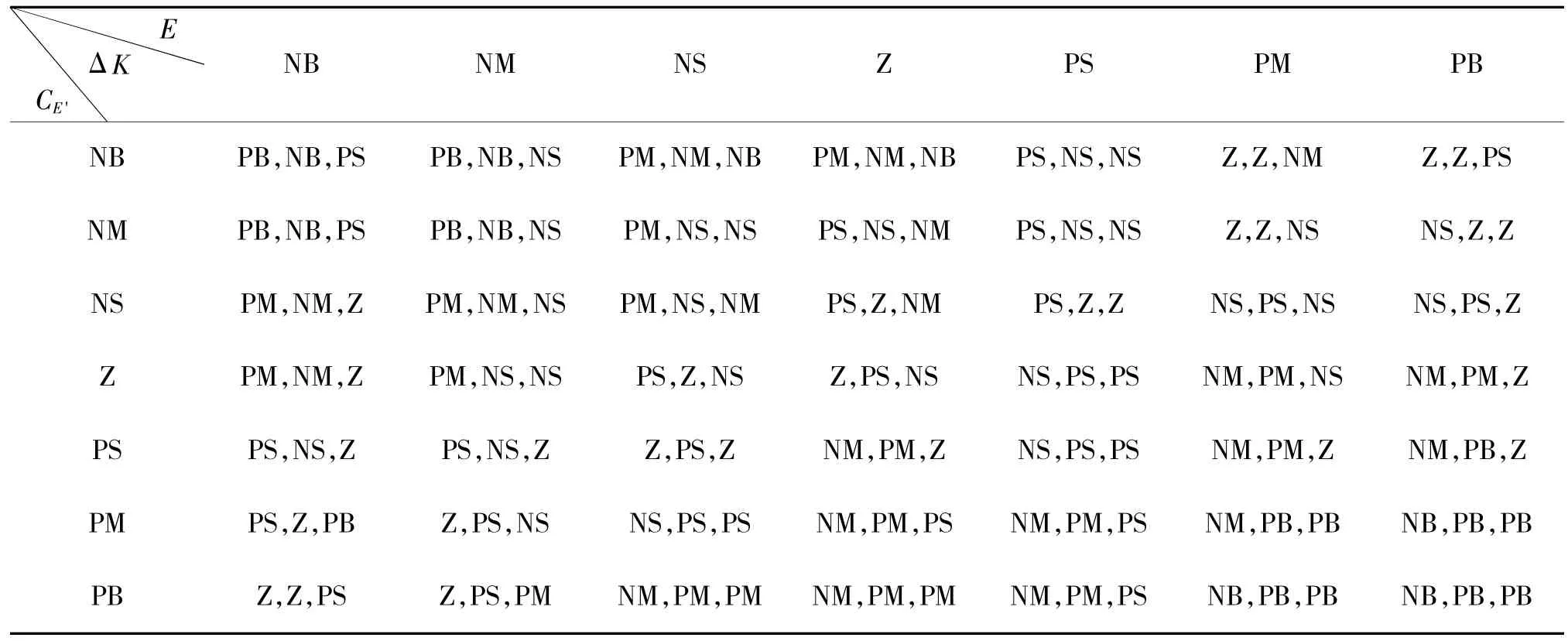
表1 ΔKP、ΔKI、ΔKD 控制表

2.4 解模糊化

误差以及误差对时间的变化率C经过模糊化处理后形成3 个模糊集合。在工业过程控制中，模糊集合不能直接作为输出。必须将模糊集合的数值进行相应代数运算，输出准确值才能实行控制。这一过程定义为解模糊化。

常用的解模糊化方法有加权平均法、重心法、最大隶属度法、三角模糊数去模糊法、面积平分法等。为了使模糊推理输出值更平滑，即对于输入信号发生微小变化，输出也会得到及时的响应。由于二级倒立摆系统在临近平衡点的控制中要求具有精度高，响应快等特点，故需要准确性较高的方法解模糊化。重心法相较于其他方法计算结果精度更高，输出更平滑，该算法的原理为：取横坐标与隶属度函数围成的面积的重心作为模糊推理的最终输出值。式（11）定义重心法的一般计算方法。

式中，是模糊集的输出元素，μ（）为该输出的隶属度函数。式（11）为单输出的计算表达式，对于多输出系统，多元量化级数离散化处理后得到式（12）的多输出离散域表达式：

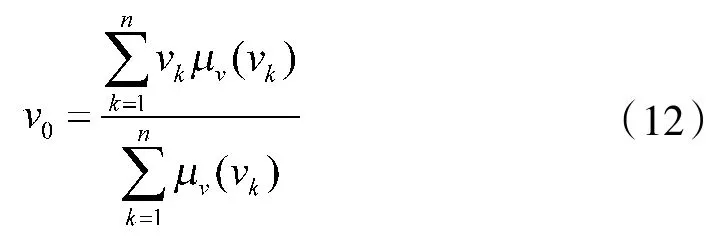
式中，元素为输出量化级数的数量。模糊集合解模糊化后得到误差和误差变化率C的精确值即PID 控制器的修正量ΔK、ΔK、ΔK。最后模糊控制器再将修正值输入至PID 控制器，实现对系统自适应控制。

3 二级倒立摆的仿真分析

3.1 无扰动仿真实验

实验环境为数字计算机，使用Matlab 软件，为验证本文提出自适应模糊PID 控制算法的有效性，针对无任何扰动的常规情况，将该算法与LQR 二次型最优控制算法、模糊控制算法、传统PID 等算法进行对比仿真实验。在Matlab 环境中，对小车在皮带上运动进行建模，并定义和输入小车的相关参量。在Similink 模块中搭建控制器，并在Matlab 中编写相应的函数。再次进行时长为30 s 的仿真，记录下小车的上下摆角和位移并画图。分析实验结果，对比模糊PID 控制器与模糊、PID、LQR 控制器控制性能的优劣。

小车的实际参量定义为：小车质量=1.096 kg，摆杆1 质量=0.2 kg，摆杆2 质量=0.1 kg，摆杆1，2 绕原点转动惯量=0.015 kg·m，摆杆1 转动中心至杆质心的距离=0.06 m，摆杆2 转动中心至杆质心的距离=0.13 m，小车与导轨之间摩擦系数=17.19，重力加速度=9.801 m·s。小车初始位置{，，}={0.2，0.1，0.2}，无扰动情况下，不同控制器控制的小车的上、下摆角，位移如图3 所示。

图3 对比仿真曲线

从图3 可以得出：在无任何扰动的环境中，常规PID 控制小车动态性能的曲线在出现较大超调量以后，逐渐趋近于稳定。这是因为PID 控制器中积分项变化率较大造成PID 控制精度不高。在实际工业过程控制中，由于各种环境参数发生变化，或是人为决策发生变化，需要PID 控制器立即进行临界参数整定，且要求整定速率快，具有实时性。这更多地依赖于操作员的经验，泛化性较差。

模糊控制相较于PID 控制，控制小车动态性能指标中的超调量明显降低，调节时间略微降低，出现超调后的收敛速率低于PID 控制。但模糊控制的上、下摆角、位移的初始阶段的波动幅度大于PID。出现这种现象的原因是因为模糊控制中信息的简单处理导致系统控制精度的降低，小车的跟随能力下降。若要提高精度就必然会增加量化级数，导致模糊规则数增加，甚至不能进行实时控制。

模糊PID 控制的小车性能具有3 种控制方法中最小的超调量、过渡时间、调节时间，且小车摆动的幅度最小，控制效果明显好于模糊、PID 方法。验证了算法在无扰动环境下控制的有效性。

3.2 随机扰动仿真实验

为考察模糊、PID、模糊PID 3 种控制方法控制二级倒立摆系统的抗扰能力，设计控制器时，在随机位置施加一扰动信号，比较加入扰动信号后，小车性能指标变化幅度。在系统运行至第2 s 时，施加扰动信号，考虑小车的摆角变化幅度最大，选小车上、下摆角进行仿真实验，得到小车摆角的曲线如图4 所示。

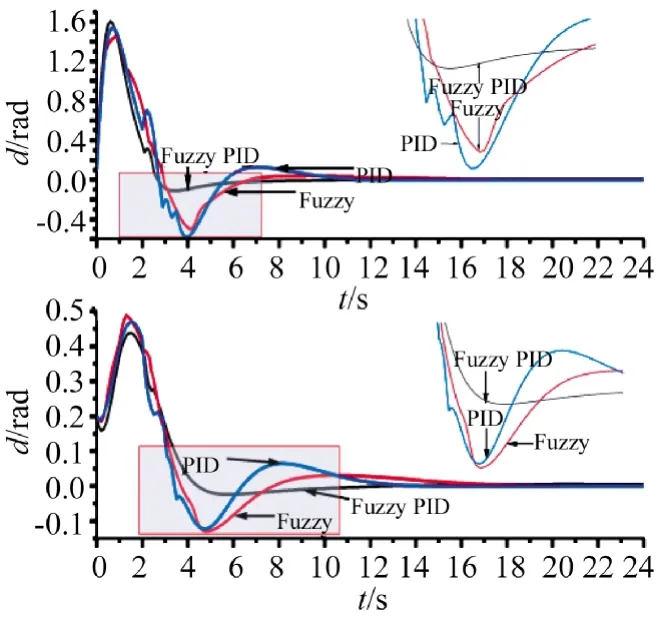
图4 上、下摆角对比仿真曲线

由图4 可知：在系统运行2 s 时施加扰动信号后，模糊PID 控制系统的上摆角、下摆角在3 s 处恢复稳定状态，模糊控制、PID 控制的上、下摆角则分别需要3.5 s和4 s 才能使系统恢复到稳定运行状态。系统在大范围渐进稳定后，模糊PID 控制小车的上、下摆角仍明显好于模糊控制、PID 控制，验证得到自适应模糊PID 算法对于外部扰动的抑制作用较好。

3.3 模糊PID 控制与LQR 对比实验

文献［9］提出了一种LQR 二次型最优控制的方法，通过调整小车摆角、位移等不同参数的权重系数，权重函数，计算得到系统反馈增益，并设置前置滤波器对数据进行滤波处理，最终使系统性能指标达到最小，使小车最终稳定在期望位置。为考察模糊PID 与LQR 方法控制二级倒立摆系统的性能好坏，以及是否存在局部最优问题，将LQR与模糊PID 控制方法做对比实验，得到仿真曲线如下页图5 所示。

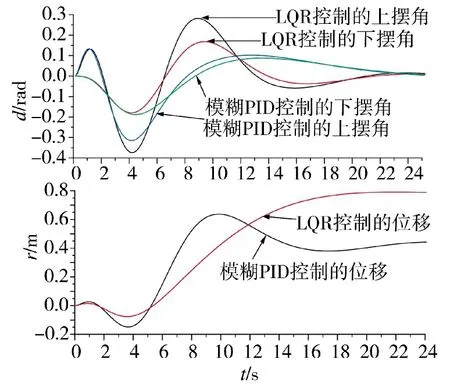
图5 LQR 与模糊PID 对比实验

由图5 可知，在二级倒立摆系统运行的前3 s，LQR 方法控制系统的上、下摆角和位移变化幅度相较于模糊PID 更小，控制性能优于模糊PID 方法。系统在控制器作用下运行一段时间后，系统动态性能不如前3 s 理想，上摆角、下摆角变化幅度相较于前3 s 增加，小车位移曲线上升时间变长。说明LQR方法控制系统性能具有局部最优的特点。模糊PID方法控制系统相比于LQR 方法具有更小的超调量、调节时间。在运行3 s 后，小车的摆角及位移变化幅度明显小于LQR 方法，控制效果好于LQR 控制器。在系统运行时加入连续2 s 的扰动后，系统的下摆角响应曲线如图6 所示。

图6 模糊PID 与LQR 受扰后对比仿真

由图6 可知，在系统收到持续扰动后，LQR 方法基本已经失效了。而模糊PID 控制依然能维持系统的小范围稳定，说明模糊PID 拥有着比LQR 更好的抗扰能力，更加适用于环境参数容易变化的场合。综合以上实验结果，使用模糊PID 控制方法实现了二级倒立摆的稳定控制。

4 结论

使用自适应模糊PID 方法对二级倒立摆控制的稳定性进行研究。结合PID 控制的广泛性、适用性与模糊控制的智能性、简化系统设计的复杂性，设计自适应模糊PID 控制器，并与PID、LQR、模糊方法做对比及抗扰实验。仿真实验表明：模糊PID方法控制二级倒立摆的动态性能良好，摆角的振幅较小，位移的最大偏移量较低。能够实现系统的大范围渐近稳定，且不需要过多人为经验先行整定PID 参数，控制的泛化性较强。此外，模糊PID 控制的二级倒立摆系统抗扰的能力较强，鲁棒性高，为二级倒立摆PID、模糊等控制方法提供了一条新思路，值得应用与推广。