考虑假数据攻击检测的动态相量估计方法

2022-03-21赵大凯赵庆生梁定康王旭平

太原理工大学学报 2022年2期

赵大凯，赵庆生，梁定康，王旭平

(太原理工大学电气与动力工程学院，太原 030024)

智能电网的高度自动化是依靠其网络通信技术与控制技术实现的，因此准确的状态估计是智能电网稳定运行的保障[1]。安装在智能电网中的传感器通过通信网络传输状态数据，如果黑客利用通信网络中的漏洞进行数据攻击，将对智能电网安全运行造成巨大伤害[2]。

对电网中相量快速精确的估计是系统状态估计和稳定运行的重要手段[3]。相量估计算法主要包括离散傅立叶算法、最小二乘法[4]以及卡尔曼算法等。离散傅立叶变换(discrete fourier transform，DFT)因其高次谐波抑制能力强、计算复杂度低被广泛应用于相量估计[5-6]。但在频率偏差、幅值和相角动态变化时，频谱泄露和非同步采样等问题导致传统DFT的估计精确度较差[7]。

卡尔曼滤波器因其优异的动态跟踪性能被广泛应用到动态相量测量中，文献[8]提出了一种非线性拓展卡尔曼算法来精确估计相量参数，虽然该方法在估计精度上有很好的表现，但当信号发生突变时，其动态响应较慢。文献[9]为了改善卡尔曼算法对动态信号的动态性能，在卡尔曼算法的基础上引入强跟踪思想，通过自适应地调整预测误差协方差矩阵，使信号发生突变时快速跟踪突变，有效解决了卡尔曼发散和动态性不足的问题。但是在量测数据存在不良数据时，上述算法的性能就受到很大影响，为解决这一问题，文献[10]提出了一种基于无迹卡尔曼的电力系统抗差估计方法，该方法通过残差来判断量测的异常值以克服不良数据的影响。

假数据注入攻击是黑客在了解系统拓扑的情况下，有目的地篡改量测数据，使控制器做出错误动作[11-12]。当量测数据的采集受到黑客的假数据注入攻击时，通过残差检测异常值的方法便失去了作用。文献[13]设计了一种假数据注入的方式，结果证明假数据注入攻击可以躲过传统的异常值检测，对系统造成危害。为此，文献[14]提出了一种基于欧几里得距离的检测器，但文献中只对系统稳态信号进行检测，并未考虑系统动态信号对检测结果造成的影响。

已有文献在检测信号时只考虑了稳态信号，当系统处于动态条件下未做考虑，且所用算法对动态信号的跟踪能力不足，因此本文建立了系统在动态条件下的信号模型，推导了动态信号的线性化表达式，通过双次优渐消因子强跟踪卡尔曼(double suboptimal-scaling factor adaptive strong tracking kalman filter，DSTKF)对信号进行估计。针对可能面临的假数据注入攻击，在DSTKF算法中引入了基于欧几里得距离的攻击检测器。最后，为了验证文章所提算法对假数据攻击检测的有效性以及对动态相量估计的动态性能，对假数据注入攻击的电气信号以及IEEE39节点系统的信号进行测试。

1 动态相量估计算法

1.1 动态相量模型

一般地，电网电压或电流信号可以表示为；

y(t)=A(t)cos(2πf0t+φ(t))+ym.

(1)

式中：A(t)为基波分量幅值，f0为电网频率额定值，φ(t)为基波分量相角，ym为信号的谐波分量。文章以信号的基波为例，对动态信号进行分析。

将y(t)改写为复指数形式为：

(2)

(3)

其中，R(i)(t0)表示R(t0)的i阶导数。假设t与t0的间隔为采样间隔ε，那么RK(t)的各阶导数可以表示为：

(4)

R(t)=Ψ(ε)R(t0).

(5)

(6)

由式(2)与式(5)联立可得：

(7)

其中，c=[1 0 … 0].将电网信号写成适合卡尔曼算法的形式：

X(n)=AX(n-1)+w(n).

(8)

y(n)=CX(n)+v(n).

(9)

(10)

C=[1 0 … 0 1 0 … 0] .

(11)

以上是对电网单相信号基波进行分解处理，信号中的谐波分量与基波分量的处理方法一样，这里不再赘述。

1.2 DSTKF算法

本小节先对卡尔曼滤波(kalman filter，KF)原理进行推导，之后将强跟踪思想[9]与卡尔曼滤波器相结合，提出双次优渐消因子强跟踪卡尔曼算法。

首先介绍卡尔曼滤波流程：

X(n,n-1)=AX(n-1).

(12)

P(n,n-1)=AP(n-1)AT+Q.

(13)

K(n)=P(n,n-1)CT(r+CP(n,n-1)CT)-1.

(14)

X(n)=X(n,n-1)+K(n)(y(n)-CX(n,n-1)).

(15)

P(n)=(I-K(n)C)P(n,n-1).

(16)

其中，P(n,n-1)是第n-1步对第n步的预测误差协方差矩阵，K(n)是卡尔曼增益，r和Q分别是w(n)、v(n)的噪声协方差。

为了增强KF算法的跟踪能力，将KF算法与强跟踪思想结合。强跟踪思想就是根据式(12)的估计值与量测值处理得到双次优渐消因子，通过双次优渐消因子对P(n,n-1)与Q进行修正，减小过去数据对K的影响，加速算法对动态信号的响应速度。DSKTF算法对公式(13)进行修正：

P(n,n-1)=α(n)AP(n-1)AT+Q(n).

(17)

Q(n)=q(n)diag{1 … 1} .

(18)

α(n)和β分别为强跟踪中的两个次优渐消因子，强跟踪中的α(n)由式(19)-(24)表示：

e(n)=y(n)-CX(n,n-1).

(19)

(20)

N(n)=V(n)-R-CQ(n)CT.

(21)

M(n)=CAP(n-1)ATCT.

(22)

(23)

(24)

其中，V(n)为残差的协方差矩阵，e(n)为根据状态量预测值求得的残差，ρ为遗忘因子，tr[ ]表示矩阵的迹。强跟踪中的β作用于q(n)，q(n)由式(25)和(26)表示：

(25)

q(n)=βq(n,n-1)+q(n-1).

(26)

式中：X1表示状态量X的第一个元素。文中β取0.9.

2 假数据攻击检测

2.1 攻击模型的建立

参考现在常见的几种数据攻击方式，文章考虑随机数攻击和假数据注入攻击作为研究对象。

2.1.1随机数攻击模型

顾名思义，随机数攻击是黑客不知道系统拓扑的情况下利用随机数干扰量测数据，被篡改的数据没有目的性。根据攻击时间的长短可以把随机数攻击分为连续随机数攻击和短期随机数攻击，其中连续随机数攻击因为攻击时间较长，所以受到攻击后被篡改数据与真实值之间差值的大小存在波动现象。随机数攻击模型可表示为：

y′(n)=CX′(n)+v(n)+r(n).

(27)

其中，y′(n)表示被攻击后的量测值，X′(n)表示受到攻击后的状态量，r(n)表示量测值所受到的随机数攻击。

2.1.2假数据注入攻击模型

在假数据注入攻击的情况下，假设黑客知道系统模型，包括卡尔曼算法中的A、C、Q、r和增益K等。例如在这种攻击模式下，黑客利用观测矩阵C可以构造一组残差估计器无法识别的假数据注入，被篡改后的量测值与估计值的残差始终保持在检测阈值以下，导致检测失效。假数据注入攻击模型可以表示为：

y′(n)=CX′(n)+v(n)+Cx(n).

(28)

其中，x(n)=|X′(n)-X(n)|，x(n)是被攻击前后的状态量误差。此时在这种假数据注入攻击下，被加入的假数据被有意设定，被攻击后计算得到的残差与攻击前几乎相同，所以残差检测器失效。

2.2 欧几里得距离检测器

因为假数据注入攻击是由黑客根据系统精心构造的，被攻击后的残差几乎没有改变，所以传统的基于残差的检测器无法检测出这类攻击。为了检测这类攻击，提出一种基于欧几里得距离的检测器。

根据欧几里得距离公式，两个m维向量之间的欧几里得距离为：

(29)

其中a、b分别为两m维向量中的元素。因此，将DSTKF算法中的状态量作为检测器检测对象，基于欧几里得距离检测器的公式为：

(30)

d(X,X′)表示受攻击前和受攻击后的状态量距离，当距离超过设置好的阈值后，便认为受到袭击或系统发生突变。经验表明，当阈值设置为3倍的噪声标准差时，便可以躲过绝大部分噪声的影响。值得注意的是，采用基于状态量的欧几里得距离检测器检测的对象是状态量。在实际检测中，本文检测器对DSKTF算法的式(15)进行检测，这就简化了运算并减少计算时间。

3 实验结果与分析

为了验证本文所提方法的有效性，对几种数据攻击模型下的信号和动态信号进行仿真。f0设置为50 Hz，考虑到实际情况会有噪声存在，测试信号均被标准差为0.2的高斯白噪声污染。设置X(0)为零向量，P(0)是以109为对角值的对角阵，检测阈值设置为0.6.实际运行中，在DSTKF计算出新的状态量后，利用检测器的检测值曲线特征对是否受到假数据攻击或电网发生突变做出判断。当认定为受到假数据攻击时，对采集数据进行剔除并重新采样，再进行相量估计。

3.1 含谐波的稳态信号测试

3.1.1随机数攻击

含谐波分量的信号测试如式(31)所示，在0.08 s分别加入短期随机数攻击和连续随机数攻击。图1为信号受到短期随机数攻击后的检测曲线。图2为信号受到连续随机数攻击后的检测曲线。

图1 短期随机数攻击检测结果图Fig.1 Short random attack detection

y(t)=cos(2πf0t)+0.1cos(6πf0t)+
0.01cos(10πf0t).

(31)

从图1可以看出，当受到短期随机数攻击时，检测值d开始增加并超过阈值，在经过约23 ms后才降到阈值以下。若检测值d符合这一特征，则判断信号受到短期随机数攻击。从图2可以看出，当受到连续随机数攻击时，检测值d开始增加并超过阈值，随后发生波动并多次超过阈值。若检测值d符合这一特征，则判断信号受到连续随机数攻击。

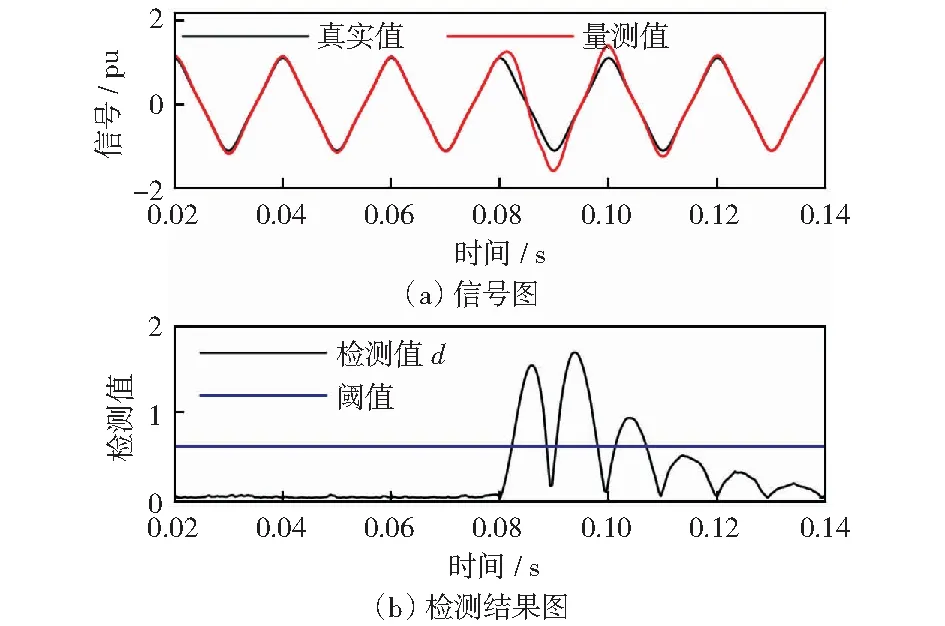
图2 连续随机数攻击检测结果图Fig.2 Continuous random attack detection

3.1.2假数据注入攻击

在0.1 s时，向式(31)所示信号进行假数据注入攻击。图3(a)是受到攻击后信号的真实值与量测值。

图3 假数据注入攻击检测结果图Fig.3 False data injection attack detection

从图3可知，在受到假数据注入攻击后，量测值与真实值之间是渐渐分离的，相邻的两个状态量之间残差始终保持在阈值以下，这也说明了传统的基于残差的检测器无法检测到这类攻击。在图3(b)中，残差检测值在受到攻击后虽然从0.01增加到0.03附近，但仍在阈值之下，而本文检测器的检测值d在受到攻击后就开始增长并超过阈值，这证明本文检测器可以有效检测假数据注入攻击。

3.2 动态信号测试

3.2.1低频振荡信号

系统发生小扰动后，电网信号的幅值相角会产生振荡。假设信号发生低频振荡，振荡幅值为0.1，振荡频率为5 Hz：

y(t)=(1+0.1cos(2π×5t))×cos(2πf0t+
0.1cos(2π×5t)).

(32)

图4为低频振荡信号的信号图及其检测结果。与稳态信号相比，因为信号的幅值相角不断变化，幅值调制信号的检测值d虽然增大至0.1附近，但未超过阈值，这并不会对检测结果造成干扰。

图4 低频振荡信号检测结果图Fig.4 Low frequency oscillation signal detection

3.2.2幅值阶跃信号

在系统发生大扰动时，电网信号常常会发生突变。假设在0.1 s时，信号幅值从1变为1.2：

(33)

图5为幅值阶跃信号图及其检测结果。图5(b)中检测值d在0.1 s时突然迅速上升超过阈值，并在大约3 ms内迅速回到阈值下。这是因为DSTKF中的双重次优渐消因子可以加速算法对历史数据的遗忘，增强了算法的动态响应速度，使得检测值迅速下落。

图5 幅值阶跃信号检测结果图Fig.5 Amplitude step signal detection

3.2.3相角阶跃信号

假设0.06 s时，信号初相角从0变为：

(34)

图6为相角阶跃信号图及其检测结果。图6(b)是与不同算法结合的检测值对比图。基于DSTKF算法的检测器的检测值特征与图5(b)类似。基于KF算法的检测器的检测值由于KF算法跟踪能力不足，检测值特征与图1(b)中受到短时随机数攻击检测值特征相似，因此基于KF算法的检测器在信号发生突变时容易发生误判。

图6 相角阶跃信号检测结果图Fig.6 Phase step signal detection

综上，当检测值d在超过阈值后短时间内回到阈值下并不再超过阈值时，判断为信号发生突变而不是受到攻击；当检测值d多次超过阈值或长时间大于阈值时，判断信号受到攻击，此时就需要对采集数据进行修正。

3.3 IEEE39节点系统信号测试

在DIgSILENT PowerFactory中对IEEE39节点系统进行仿真。在1 s时，对系统中的8号发电机进行切机；1.4 s时，黑客对数据采集系统进行假数据注入攻击。

节点15的信号测试结果如图7所示。图7(a)为信号图，信号在1 s发生突变后开始振荡。从图7(b)可以看出检测器共超过阈值两次。在1 s时可以判断为系统发生大扰动，在1.4 s时可以判断为数据采集系统受到假数据注入攻击。图7(c)是信号幅值估计的局部放大图，DSTKF算法在扰动发生后20 ms后信号完成跟踪，并对后续的振荡信号保持平稳跟踪，幅值估计最大误差为0.062%，远高于标准所要求的3%.KF算法在扰动发生后约70ms后才完成跟踪，且在跟踪振荡信号时产生波动，幅值估计最大误差为2.4%.因此，当系统发生扰动时，DSTKF算法在跟踪速度和精度上均优于KF算法。