一种星载VDES接收机多通道碰撞信号分离算法
2022-03-17赵丹,黄敏
赵 丹,黄 敏
(1.南京理工大学紫金学院 电子工程与光电技术学院,江苏 南京 210023;2.南京理工大学 电子工程与光电技术学院,江苏 南京 210094)
甚高频数据交换系统(Very-high-frequency data exchange system,VDES)是由国际航海标准协会和国际电信联盟共同提出的新一代海上数据交换系统。该系统作为船舶自动识别系统(Automatic identification system,AIS)的升级版,增加特殊应用报文(Application specific message,ASM)和甚高频数据交换(VHF data exchange,VDE)两个子系统[1],传输数据内容和形式更丰富,为船舶提供身份识别、位置报告等服务,是海上通信的主要工具和航行安全的重要保障。星载VDES系统的出现虽然在一定程度上缓解了星载AIS链路负载,但依旧存在信号时隙碰撞的问题[2],会造成船舶信息的丢失,影响航行安全,因此星载VDES接收信号的碰撞分离成为系统应用亟待解决的重要问题。
混合信号的盲分离一直是信号处理领域研究的热点问题,近年来被广泛应用于无线通信系统中。针对通信侦察中混合信号的分离,付卫红等[3]提出基于独立成分分析(Independent component analysis,ICA)的盲分离算法;为了解决无线通信中的自干扰消除问题,Mohammed等[4]提出一种改进的Fast ICA盲分离算法;文献[5]采用基于自相关矩阵特征值分解的盲分离算法,实现了DS-CDMA系统中用户数据与扩频码的分离与估计;文献[6]提出一种基于分级迭代的变步长等变自适应分离(Equivariant adaptive separation via independence,EASI)算法,完成了AIS碰撞信号的分离。对于星载VDES系统中信号碰撞分离问题,目前的研究主要是针对适定或者超定(观测信号数量大于源信号数量)情况下开展的[7,8],而实际应用中卫星载荷因体积、重量、功耗的限制使得接收机路数即观测信号路数应该尽量少,所以欠定情况下的碰撞信号分离算法具有非常重要的实际应用价值。
本文提出一种基于随机近端梯度张量分解的VDES碰撞信号多通道分离算法。这算法不仅可以实现适定或者超定情况下的分离,而且适用于欠定情况下的分离。首先基于广义协方差矩阵建立张量分解模型,利用塔克分解压缩张量得到核张量,可以显著减少张量分解的计算复杂度,之后引入随机近端梯度(Stochastic proximal gradient,SPG)算法对核张量标准分解的过程进行优化,提高分解精度,最终完成对碰撞信号的高效分离。
1 多通道碰撞信号分离模型
星载VDES系统采用天线阵列接收架构,碰撞信号分离模型如图1所示。
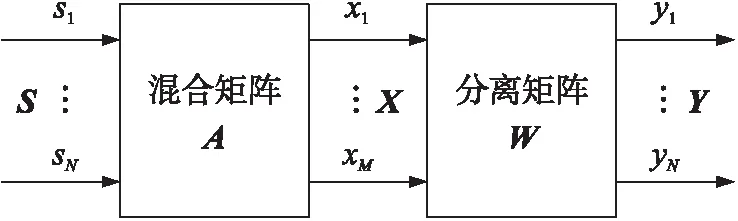
图1 碰撞信号分离模型
图1中,S=(s1,s2,s3,…,sN)T∈RN×T为N路源信号,X=(x1,x2,x3,…,xM)T∈RM×T为M路观测信号,T为采样点数。混合矩阵A=(aij)∈RM×N中aij(i=1,2,…,M,j=1,2,…,N)为第j路源信号到接收机第i路接收信号的混合参数,模拟信号碰撞的过程,满足关系
X=AS
(1)
Y=(y1,y2,y3,…,yN)T∈RN×T为最终得到的N路分离信号。碰撞信号盲分离的过程就是在混合矩阵A和源信号S未知的情况下,只根据观测信号X求解分离矩阵W=(w1,w2,w3,…,wN)T∈RN×T,进而得到分离信号Y=WX。当M等于N时为适定盲分离问题,当M大于N时为超定盲分离问题,当M小于N时为欠定盲分离问题。
当M小于源信号数量N时,混合矩阵A∈RM×N不再是满秩矩阵,常用的独立成分分析[3,4]和等变自适应分解[6]等信号分离算法已不再适用,当A和S满足以下条件[9],可以采用张量分解进行求解:
(1)A的列向量两两线性无关;
(2)A的任意M×M子矩阵都为非奇异矩阵;
(3)S必须为非高斯信号。
对M路观测信号进行中心化处理使得信号具有单位方差,并对其进行白化处理可以消除信号之间的相关性[10]。而对于某一路源信号,星载VDES系统多路天线都会收到该路信号的加权信号,并且接收通道之间是独立的,所以混合矩阵A的任意M×M子矩阵都为非奇异矩阵,同时VDES系统源信号也是非高斯的,满足采用张量分解进行欠定情况下求解的条件。
2 基于随机近端梯度张量分解的碰撞信号分离算法
由天线阵列接收星载VDES系统碰撞信号,然后通过模数转换器采样获得多路数字信号,并进行数字下变频处理,获得观测信号矩阵。设观测信号为X∈RM×T,源信号为S∈RN×T,其中观测信号路数M的值小于或等于源信号路数N的值,即为欠定或适定情况。

在线性瞬时混合模型下,采用预处理后的观测信号X′的广义协方差矩阵ΨX作为核函数,它描述了混合矩阵和观测信号广义协方差矩阵之间的关系,用K个不同延迟处理点τ1,τ2,…,τK的核函数提取统计信息,建立张量分解模型,表示为[11]
(2)
式中:ΨX为观测信号广义协方差矩阵,ΨS为源信号广义协方差矩阵,AT为混合矩阵A的转置。
将K个广义协方差矩阵进行堆叠,得到张量χ∈RM×M×K,其中每个元素表示为
k=1,2,…,K
(3)
定义矩阵D∈RK×N,使其第k行的第n个元素对应对角矩阵ΨS[ATτk]的第(n,n)个元素,即
(D)kn(ΨS[ATτk])nn
k=1,2,…,K;n=1,2,…,N
(4)
则张量χ的元素值可表示为
(5)
式中:ain和ajn均为混合矩阵A中对应的元素,dkn为矩阵D的元素值。式(5)可以进一步用向量外积的形式表示为
(6)
式中:an和dn分别为混合矩阵A和矩阵D的列向量,∘表示向量外积。
式(6)将张量χ分解为N个秩一分量之和,是一个标准分解形式。但是该分解与所取处理点数K有关,为了得到更精确的结果,当K取值较大时,容易出现复杂度高、计算时间长和收敛速度慢的问题。因此为加快标准分解的计算速度,可以在进行分解之前先采用Tucker分解对观测信号构建的张量χ进行压缩,使其成为一个低维的核张量,之后再对核张量进行标准分解得到混合矩阵。
由于广义协方差矩阵为对角矩阵,因此可以将张量χ按三个维度展开为模n(n=1,2,3)矩阵形式,分别为χ(1)∈RM×MK、χ(2)∈RM×MK、χ(3)∈RK×MM,这三个矩阵的秩称为张量χ的n-秩,表示为
rankn(χ)=rank(χ(n))=Nn=1,2
rank3(χ)=rank(χ(3))=LL≤K
(7)
固定Tucker分解中的两个因子矩阵为单位矩阵I∈RM×M,即进行Tucker-1分解,则其表达式为
χ=γ×1Ι×2Ι×3U
(8)
式中:γ∈RM×M×L为核张量,×n(n=1,2,3)为张量与矩阵的n模乘积,U∈RK×L为列酉矩阵。用矩阵的Kronecker乘积形式表示为
χ(3)=Uγ(3)(I⊗I)T=Uγ(3)
(9)
式中:χ(3)、γ(3)为张量χ和γ的模3矩阵,⊗表示Kronecker积。式(9)就是χ(3)的主分量分解形式,所以U是χ(3)的前L个左奇异向量组成的矩阵[12],可以通过χ(3)的奇异值分解得到。在求得U后可以计算核张量
γ=χ×1Ι×2Ι×3UT=χ×3UT
(10)
这样就将M×M×K的张量χ压缩为M×M×L的核张量γ,下面只需要对核张量γ进行标准分解来求解混合矩阵A。因为Tucker分解的第一、第二因子矩阵是单位矩阵,所以核张量γ也是一个对称张量,其标准分解表达式为
(11)

(12)
将核张量写成标准分解形式
(13)

f(B(1),…,B(Q))=
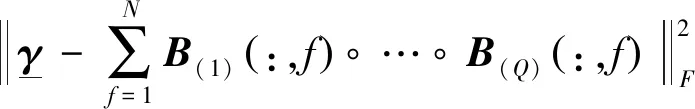
(14)
式中:‖·‖F为Frobenius范数。采用随机近端梯度(Stochastic proximal gradient,SPG)算法求解,第r次迭代更新公式为[13]
(15)
(16)

(17)
式中:υn为核张量γ的某一个模n纤维,H(n)为除B(n)以外剩余因子矩阵的Khatri-Rao乘积
H(n)=B(1)⊙…⊙B(n-1)⊙B(n+1)⊙…⊙B(Q)=
(18)
步长α更新公式为
(19)
式中:β为步长调节因子,是一个非常小的值,这里取10-6;α(r)|r=0为初始搜索步长,反映了搜索的精细程度,取值一般为0.001到0.1之间。
重复上述迭代过程直到目标函数达到设定值,或者达到设定的迭代次数,获得混合矩阵A的最终估计。再对混合矩阵A求逆,得到分离矩阵W,最后将分离矩阵W与混合信号矩阵X′相乘,获得分离信号。对N路分离信号进行帧头检测、频偏估计和解调译码处理,得到VDES各子系统信号的数据帧。
星载VDES系统碰撞信号分离处理步骤如下:
(1)利用N路天线接收信号,并对N路通道的观测信号进行中心化及白化预处理;
(2)根据式(2)建立不同处理点处的广义协方差矩阵集,并将其堆叠成一个三阶张量χ,该张量的矩阵因子与混合矩阵A相关;
(3)利用Tucker分解对张量χ进行压缩,得到维数更低的核张量γ;
(4)根据式(14)建立需要优化的目标函数;
(5)设置迭代参数的初始值,包括设置当前迭代次数r为0,最多迭代次数rmax,确定初始步长α(r)|r=0,随机选取核张量γ的一个模n纤维υn;
(8)计算下一次更新方向所需的步长α(r+1);
(9)对迭代次数r进行自增1操作,重复步骤(6)到(8),直到目标函数达到极小值,或者达到设定的迭代次数,获得混合矩阵A的最终估计;
(10)对混合矩阵估计求逆,得到分离矩阵估计W的估计,并将分离矩阵与观测信号矩阵相乘,最终得到源信号的估计。
3 实验分析
采用本文提出的随机近端梯度张量分解算法分别对适定和欠定情况下的碰撞信号进行分离,并基于MATLAB进行仿真实验。通过观察分离信号波形与源信号波形的相似程度可以看出分离算法对源信号波形的还原程度,用相关系数评价分离效果;实际应用中,星载VDES接收系统需要最终解出报文码元,所以同时用分离信号误码率作为评价分离效果的依据。
首先针对适定情况,设置碰撞源信号路数和接收通道路数均为4,接收信号信噪比为15 dB,源信号、观测信号以及分离信号局部波形分别如图2(a)、(b)、(c)所示,为了便于对比源信号和分离信号波形,观察分离效果,对所有信号都进行幅度归一化处理。为了进一步分析性能,将随机近端梯度(SPG)张量分解算法和经典的交替最小二乘(Alternating least squares,ALS)张量分解算法进行比较,两种算法在不同信噪比下的相关系数和分离信号误码率曲线如图3和图4所示。
对比图2(a)和(c)可以看出,源信号和分离信号对应的局部波形几乎完全一致。由图3可得,此时的相关系数接近1,同时可见,ALS张量分解算法和本文提出的SPG张量分解算法均能对碰撞信号进行有效分离,相关系数随着信噪比的增大而趋于1。图4表明误码率随着信噪比的增大逐渐变小,在低信噪比时两种算法的差异不大,随着信噪比的增大,SPG张量分解算法比ALS张量分解算法误码率更低,信噪比大于12 dB以后在误码率性能上有大于1 dB的提升。这主要归功于随机近端梯度算法拥有更好的全局搜索能力,可以有效避免陷入局部最优的情况,因此分离的性能也会优于经典的ALS张量分解算法。
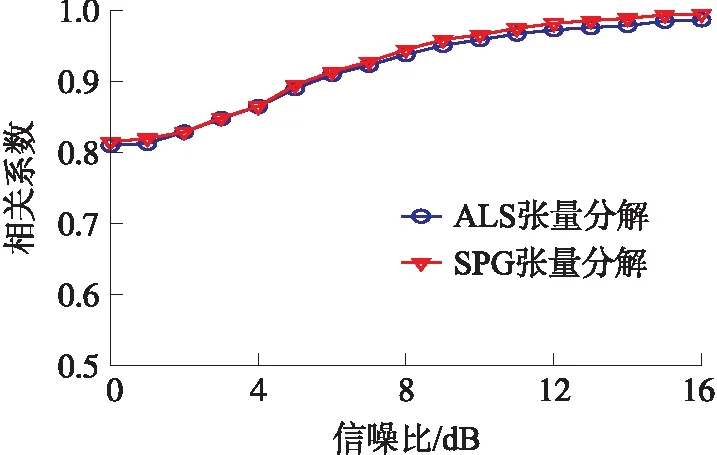
图3 适定情况下相关系数曲线

图4 适定情况下分离信号误码率曲线
接下来针对欠定情况,设置碰撞源信号路数为4,接收通道路数为3,接收信号信噪比为15 dB情况下的源信号、观测信号以及分离信号局部波形分别如图5(a)、(b)、(c)所示,相关系数和分离信号误码率曲线如图6和图7所示。

图5 欠定情况下分离信号与源信号局部波形对比图
由图5可见,虽然接收信号路数少于源信号路数,但是分离信号波形仍然可以非常精确的逼近源信号波形。图6显示,欠定情况下,SPG张量分解算法仍然能将源信号进行有效分离,信噪比大于10 dB时相关系数在0.95以上。由图7可见,SPG张量分解算法在信噪比大于12 dB时相对于ALS张量分解算法误码率性能有1 dB以上的改善,同时可以看到,两种算法在欠定情况下的误码率性能与适定情况下相比,有0.5~1 dB的信噪比损失。由于VDES卫星为低轨卫星,部署在500~2 000 km的轨道,接收信号信噪比大于16 dB,由图7可见,此时误码率在10-4以下,可以满足VDES系统对通信性能的要求,采用三通道接收机就可以实现四路碰撞信号的接收分离和解调解码,对于星载接收机小型化设计具有重要的意义。

图6 欠定情况下相关系数曲线

图7 欠定情况下分离信号误码率曲线
4 结束语
本文为解决在欠定情况下星载VDES信号碰撞问题提出了一种基于随机近端梯度优化的张量分解算法。该算法在经典张量分解算法的基础上进行改进,采用Tucker分解压缩张量减小计算复杂度;随机近端梯度算法的引入使求解过程得到进一步优化。仿真实验结果表明,本文所提出的随机近端梯度张量分解算法对于适定和欠定情况下多路碰撞信号均取得很好的分离效果,适用于星载VDES接收系统对于碰撞信号的处理。
