压电微镜薄板的大挠度弯曲偏转角解析
2022-03-16杜永飞
杜永飞,孟 江 ,范 伟,刘 凯,蒋 童,安 坤
(1.中北大学 机械工程学院,山西 太原 030051;2. 中北大学 电气与控制工程学院,山西 太原 030051)
0 引言
目前在激光通信领域中,首要任务是实现精确控制光束偏转角度,一维微镜构件已运用到该领域中[1-2],能实现在单方向上对光束的偏转控制。为了实现同一结构在两个方向上同时进行光束偏转角度跟踪控制的目标,需要设计出二维微镜结构。娄利飞等[3]制成一种基于压电薄膜逆压电效应的新型集成微镜,并对其功耗问题及机械性能进行了分析。随着我国通信事业的不断发展,激光通信技术覆盖面越来越广,研究矩形板问题也越来越有实际意义。20世纪,学者们广泛开展了关于激光通信的研究,验证了激光通信的概念。在激光通信中,由于激光传输方向高度集中,故在激光通信中光束方向的精确控制极为重要[4]。在光束偏转技术领域中,最重要的部分是能实现对光束的精确控制,如利用压电驱动的微镜使光束偏转更快速与稳定[5],在该领域得到较广泛的应用。由于压电陶瓷(PZT)材料的迟滞及蠕变、非线性等特性[6],其偏转角度的精度达不到预想值,目前通过迟滞建模及复合控制方案可消除材料的迟滞特性。本文以压电微镜薄板为研究对象[7-10],通过力学推导得到微镜挠度的一般表达式,其次运用COMSOL仿真得到不同电压条件下的数据,通过搭建压电微镜薄板的实验平台采集实验数据并进行对比,运用Matlab软件拟合仿真数据,验证了本文所提出挠度表达式的正确性与有效性。
1 压电薄板微镜
压电微镜是一种应用压电效应或逆压电效应来改变微晶的垂直距离,从而达到光束偏转的一种微机电系统的微执行器,目前应用于很多领域。李庆燕等[11]通过控制微机电系统(MEMS)微镜的驱动电压对激光雷达进行实时可变视场扫描。该二维微镜结构设计为3层薄板与4个梁的组合结构,4个梁分别固定在薄板4条边的顶点处,4个梁结构设计简单,与微悬臂梁相比,其性能更优越,结构稳固且不易断裂。因为4个梁结构具有良好的抗振能力,其端部固定,支撑压电材料,该设计具有更好的抗应变疲劳性能,如图1所示。薄板结构材料从上往下依次是Au、PZT-5A、Si,厚度分别为1 mm、3 mm、30 mm,取厚3 mm、长宽为10 mm×10 mm的压电陶瓷薄板。Au层在光束偏转中起光束反射作用,压电陶瓷层是整个微镜结构的驱动层。图2为材料示意图。在外加电场作用下,压电陶瓷发生逆压电效应,从而带动整个微板产生位移。在固定4个梁的根部时,对4个梁沿其厚度方向施加电压,仿真压电微镜薄板在此条件下的挠度变化。根据弹性力学相关知识,矩形薄板在上述边界条件下施加均布力载荷时,满足在自由边界条件下的纯弯曲条件。本文通过弹性力学知识推导计算薄板弯曲挠度表达式可知,薄板的边界条件与四边自由边界条件相似,故运用理论知识推导计算,并结合仿真数据与实验数据得出相关验证与结论。
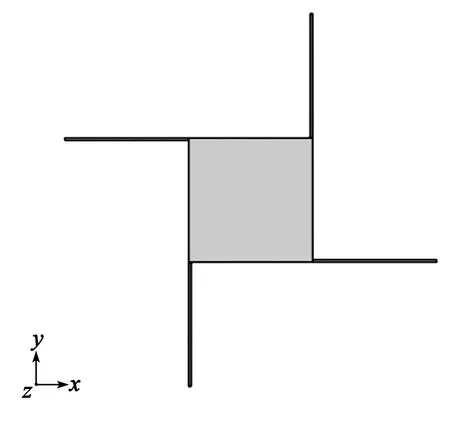
图1 微镜结构俯视图

图2 微镜结构侧视图
2 弹性力学挠度解析
大挠度弯曲薄板,根据卡门方程(Kbrman equation)即薄板大挠度弯曲组求解:
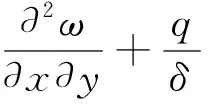
(1)
(2)
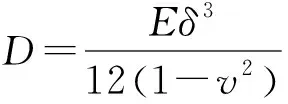
对于该薄板大挠度弯曲问题,采用变分法进行求解,其主要步骤如下:
1) 选取满足边界条件的挠度表达式。
2) 通过对该挠度函数的变分,求出适合所取挠度表达式的应力函数表达式。
3) 用里茨法求解横弯曲问题,最后确定挠度函数的表达式。
如图3所示[12],取矩形板边长为a、b的中央为坐标原点,x、y轴分别平行于薄板的两边,z轴向下为正方向。本文中微镜结构仿真是在梁的厚度方向施加压电载荷,可将其等效为在板的4个边上作用均布力矩,沿薄板的自由边界x=±(a/2),y=±(b/2)分别作用有均布力矩M1,M2。 因为平板两对边的力矩相同,因此,沿坐标轴x与y的板内各点弯矩无变化,即Mx=M1,My=M2。
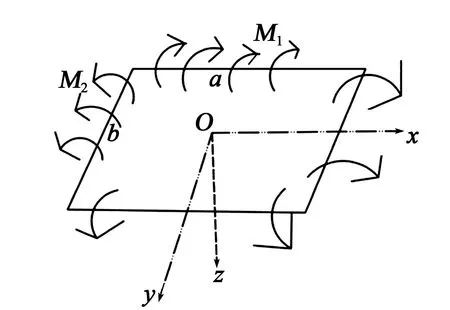
图3 矩形薄板的纯弯曲
平板的挠曲面方程为
(3)
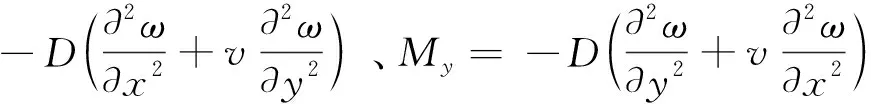
ω=d1x2+d2y2+d3xy+
d4x+d5y+d6
(4)
式中d1,d2,d3,d4,d5,d6均为未知系数。
绕y、x轴的力矩平衡条件为
∑Mx=0
(5)
∑My=0
(6)
由式(5)、(6)可得:
(7)
式中FSx、FSy为板的横向剪力。
将式(3)代入式(7)可得:
(8)
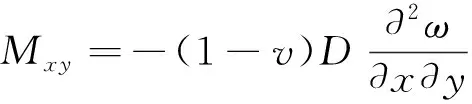
(9)
(10)
(11)
(12)
故可得该条件下薄板挠度为
(13)
将式(13)代入式(3)、(7)可得Mx=M2,My=M1,Mxy=0,FSx=0,FSy=0,验证了该挠度表达式满足该边界条件。
图4 高斯曲率为正的曲面
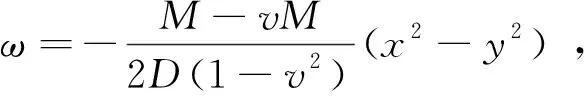
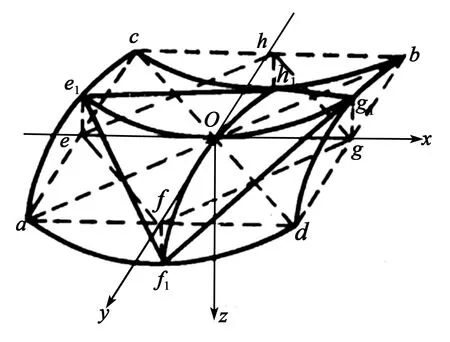
图5 高斯曲率为负的曲面
3 COMSOL仿真与Matlab拟合
3.1 COMSOL仿真
图6为COMSOL仿真模型。与薄板微镜相连的4个梁尺寸(10 mm×0.2 mm)相同,且厚度与薄板厚度一致。其边界条件为在4个梁的上表面施加垂直向下的同向均布电压载荷,4个梁的根部固定,并添加重力加速度,根据李法新等[13]对PZT材料的研究,得到PZT压电材料的相变电场为180~200 kV/cm,根据U=E×d(其中,U为相变电压,E为相变电场,d为材料的厚度)可得,PZT压电材料的相变电压约为60 V,故设置2个方向上的电压为0~60 V,并间隔5 V电压,对其进行不同电压下的仿真,其仿真条件如图7所示,图中h0,h1为在两个方向上施加的电压。仿真压电微镜薄板的材料和结构参数如表1所示。
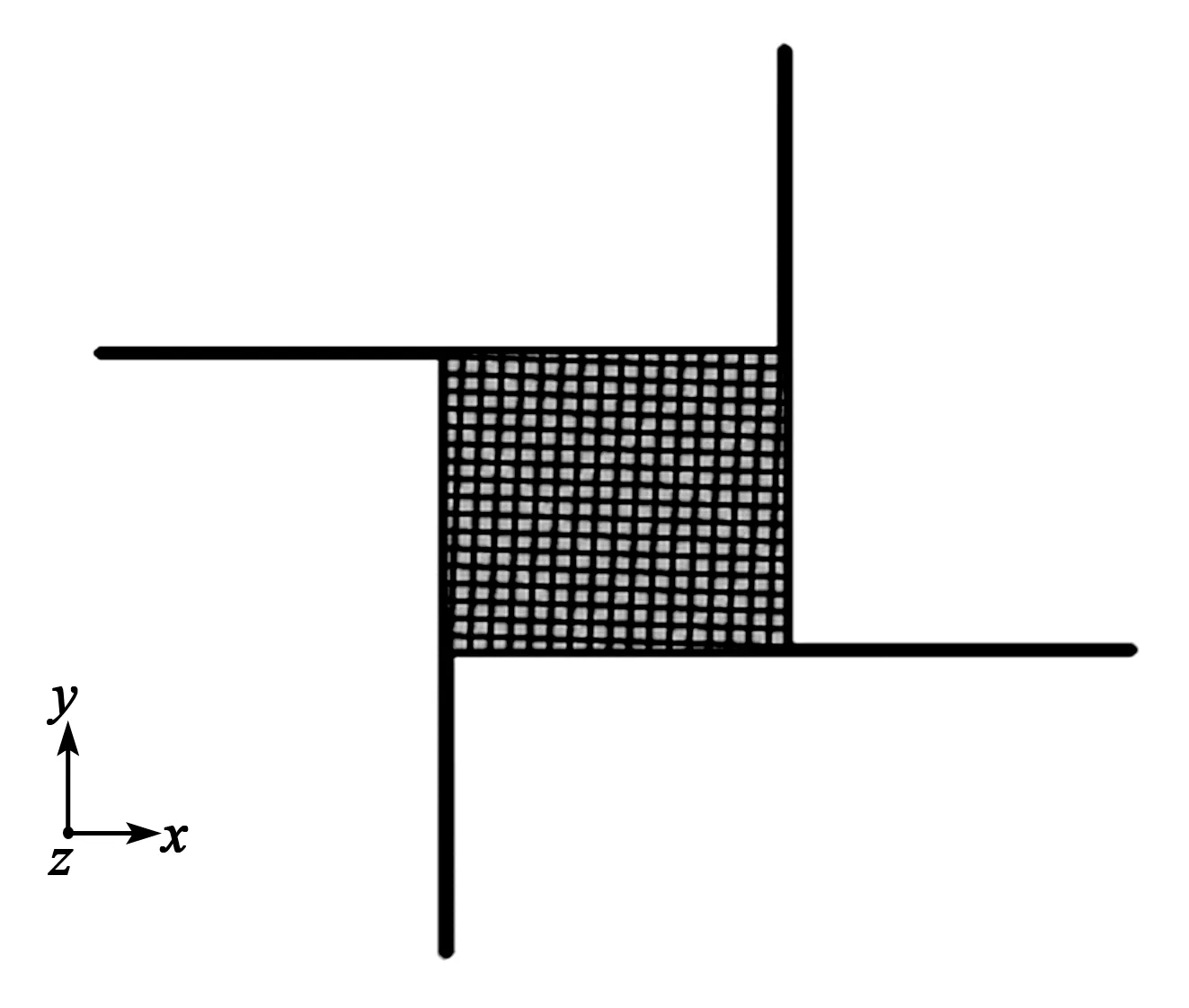
图6 压电微镜薄板
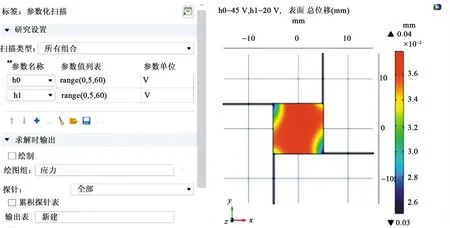
图7 仿真条件
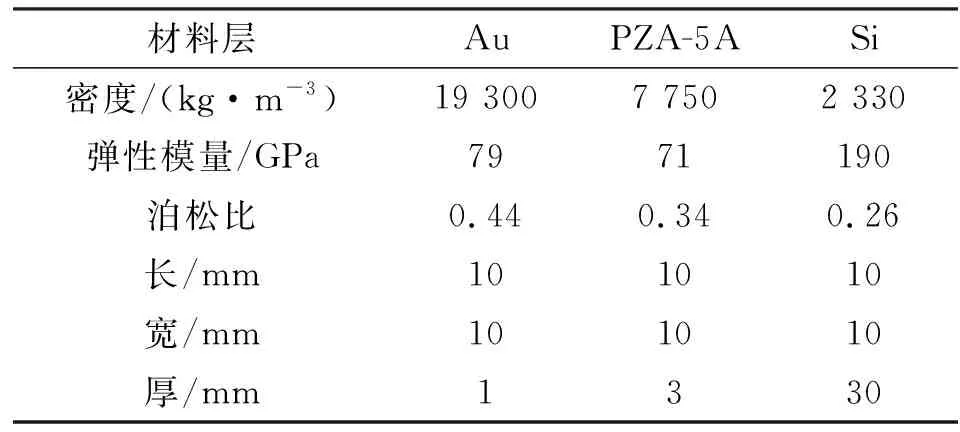
表1 压电微镜薄板材料参数
由压电理论可得,在机械自由和电学短路边界条件下的应力T、应变S和电场强度G、电位移H之间的本构方程为
(14)
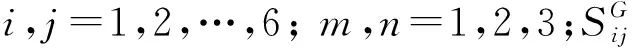
由式(14)可知,在施加应力或电压时,压电微镜会产生电位移与应变,其与所加应力及电场强度的大小呈线性关系。
运用COMSOL软件进行仿真,其网格为四边形网格,单元数为392个。在确定上述尺寸参数及材料系数的前提下,仿真分析了在梁施加均布电压载荷时,COMSOL中薄板位移变形图如图8所示。图中,h0、h1分别为两个方向上施加的电压。仿真不同电压下的部分数据如表2所示。

图8 压电陶瓷薄板变形云图
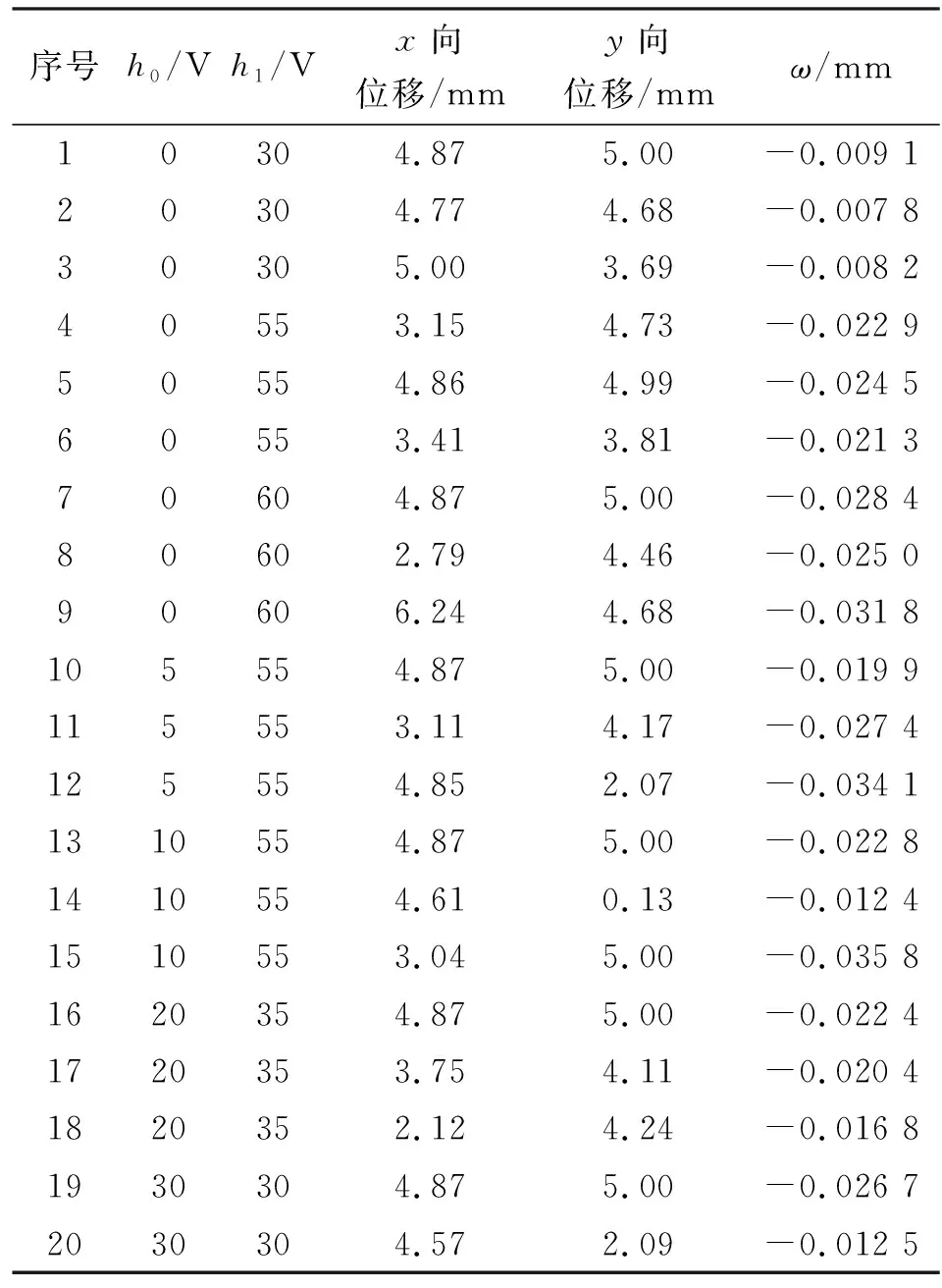
表2 仿真数据
3.2 Matlab拟合
根据仿真得出不同电压下的数据,并结合弹性力学可知,薄板在该四边自由且施加电压的边界条件下,其挠曲面与高斯曲率为正的曲面相似,故将微镜挠度表示为
ω=Ax2+By2+Cxy+D0x+
E0y+F
(15)
式中:A、B、C、D0、E0、F均为待定系数。
在该仿真条件下,两个方向施加的电压决定微镜的位移,故式(15)中未知参数与电压U、V有关。运用Matlab软件拟合两个方向上电压的关系,其拟合度R2=0.999 6,拟合式f(x,y)=ax+by+c(a,b,c为常数),均方根误差为0.000 235 6,和方差为3.885×10-7,在4个梁上施加两个方向上的电压的关系为
U(x,y)=p0×Ux+p1×Uy+p2
(16)
式中:U(x,y)为在x、y方向上同时施加的电压;p0、p1、p2为常数;Ux为x方向上施加的电压;Uy为y方向上施加的电压。
结合式(15)、(16)微镜挠度可表示为
ω=(l1U+l0)x2+(m1V+m0)y2+
(n1U+n2V+n0)xy+(o1U+o0)x+
(p1V+p0)y+(q1U+q2V+q0)
(17)
式(17)为电压U=0、V=0时的边界条件,其ω=0时可得l0=m0=n0=o0=p0=q0=0,则式(17)可变为
ω=l1(x2U)+m1(y2V)+n1(Uxy)+
n2(Vxy)+o1(Ux)+p1(Vy)+
q1U+q2V
(18)
式(18)适用于压电微镜薄板结构在四边自由的边界条件及在两个不同方向施加电压的条件。
将式(18)看为ω=a1A1+b1B1+…,其中a1、b1、…是未知系数,a1、B1、…是电压U、V及坐标值x、y共同作用的结果。根据COMSOL软件的数据,选取120组不同电压下的挠度数据,运用Matlab软件进行多元一次线性拟合,其拟合计算框图如图9所示。

图9 拟合计算框图
其拟合值与实际值的最大误差为0.000 5 mm,拟合度R2=0.999 7,其拟合曲线与实际曲线如图10所示。

图10 拟合曲线与实际曲线
运用Matlab软件拟合了在不同电压下微镜的挠度表达式(见式(18))与理论推导得出的挠度曲线表达式(见式(19))一致,验证了该挠度表达式的准确性。
3.3 压电微镜的偏转角
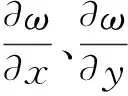
θx=2a1UX+a3UY+a4VY+a5U
(19)
θy=2a2VY+a3UX+a4VX+a6V
(20)
由式(19)、(20)可知,在四梁施加不同方向上的电压时,压电微镜可优先选出偏转角较大的一个位置。运用Matlab软件对微镜挠度进行仿真分析,得出电压U、V对微镜挠度的影响权值为0.924 8,与理论结论符合;其次,在压电微镜薄板中,通过微镜的ω可得微镜最佳的工作区域及最大偏转角位置,对于实现光束的精跟踪控制有重大的意义。
4 实验测试
4.1 实验台搭建与采样
微镜测试系统由开关电源、笔记本电脑、激光位移传感器(LK-H022K)、直流电源(型号为UTP3315TFL-Ⅱ)及压电微镜及其支撑架构成,实验平台如图11所示。通过笔记本电脑的软件控制激光位移传感器的采样频率,在该实验中设置时间为500 ms,将激光位移传感器与电脑相连,用于记录与储存测试数据,该激光位移传感器可适用于高频率振动,其自带数据采集装置。然后可通过调节直流电源的电压测试不同电压下的数据。

图11 实验测试平台
4.2 测试数据与仿真数据对比
测试中采集的数据点为压电微镜薄板的中心点,其测试数据如表3所示。运用COMSOL软件仿真在相同电压条件下得到的数据如表4所示。
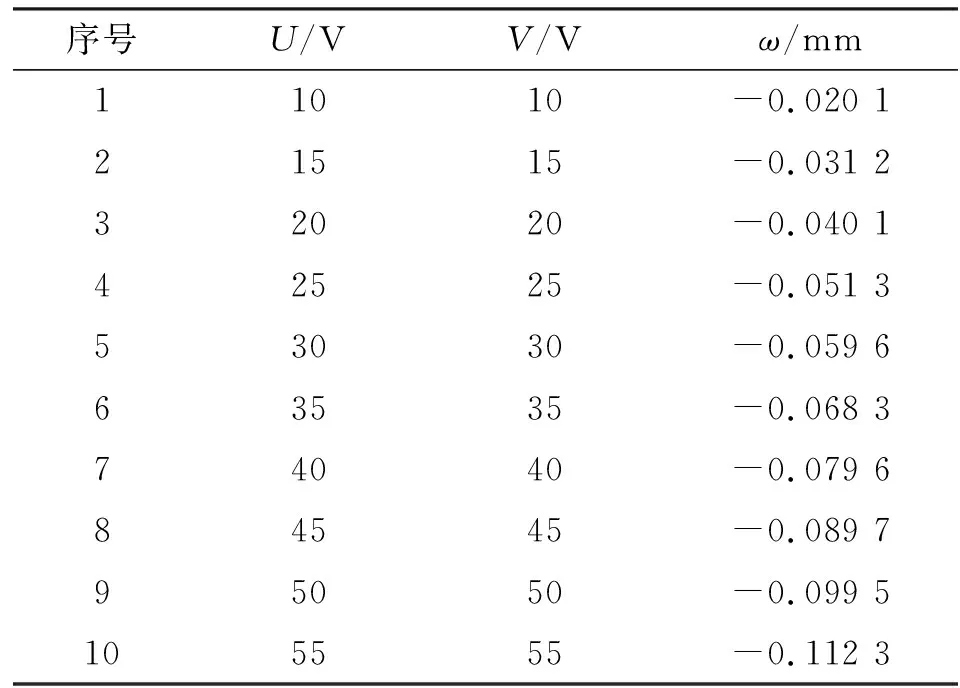
表3 实验数据

表4 仿真数据
通过对比实验数据与仿真数据,挠度值相差最大为0.006 7 mm,验证了仿真数据与测试数据的一致性。
5 结束语
利用COMSOL仿真软件对压电微镜进行了仿真,并结合弹性力学相关知识对其挠曲形式进行了理论的假设与推导。通过搭建实验平台,测得在相同电压条件下仿真数据与测试数据基本相同,验证了仿真数据的真实性。通过Matlab软件对其仿真得出的数据进行多元线性拟合,得出其拟合值与仿真值的最大误差为0.000 5 mm,拟合相关系数R2=0.999 7,得出压电微镜挠度的一般表达式,运用Matlab仿真得到电压对微镜挠度影响的权值与理论值相符。最后通过偏转角计算公式得出微镜最佳工作区域,为实现光束的精跟踪控制提供了理论基础。
