固体中二维纵波非线性方程的摄动解

钱昕彤，韩庆邦，苏娜娜，钱佳文，柏 乐，单鸣雷

(河海大学物联网工程学院，江苏 常州 213022)

0 引 言

大振幅声波在固体材料中传播时，与该固体介质相互作用，会产生波形畸变、声饱和、声波与声波非线性相互作用等一系列的非线性现象[1]。例如，声波在传播过程中会产生高频声波信号，其频率往往是原始信号的整数倍，这种现象被称为高次谐波现象。此时，线性声波的叠加定理不再适用，需要对固体中非线性声波特性进行研究，而研究非线性声波方程是常见的研究思路之一。基于固体中的弹性波理论，Landau等[2]和 Murnaghan[3]很早就研究了固体介质中的非线性声学问题，得到了各向同性介质中的非线性声波方程。研究表明此类非线性声波方程可以很好地描述声波在非线性固体材料中的传播特性[4]。对固体中非线性弹性波特性的研究，此类问题归结于经典非线性问题，是非线性声学研究及应用的理论基础。

目前，关于此类非线性声波方程的研究大多聚焦于一维情况。已有研究者通过采取不同的方法对此类非线性声波方程进行求解，得到了不同形式下的一维非线性声波的解析解[5-6]。由于固体中的非线性声波方程十分复杂，很难得到精确解，而摄动法是解决此类非线性问题的常用方法之一，通过对方程进行相应的摄动展开，常常可以得到具有相应精度的解析解。因此，部分研究者采用摄动法求解得到方程的近似解[7-9]。张世功[10]利用摄动法对纵波激发与横波激发两种情况下的一维非线性方程进行了详细求解。吴先梅等[11]对非线性纵波方程进行三阶摄动展开，得到了非线性纵波方程的三阶摄动解。吕文翰等[12]围绕声马赫系数对一维非线性方程的解进行摄动展开，从而得到了高阶摄动解。He[13-14]基于同伦摄动法对多种非线性方程进行了详细求解，这种新方法可以很好地得到非线性方程的摄动解。Ezzati等[15]基于He的研究，利用同伦摄动法求解非线性波动方程，进一步提升了求解精度。上述研究者对此类一维非线性声波方程进行摄动近似求解，并得到相应的解析解。但对于更复杂的高维度的问题，人们暂时还没有更好的研究方法。

非线性声学方法在微损伤检测中的应用，此类问题归结为非经典非线性问题[16]，主要研究由微小缺陷(早期位错疲劳损伤、疲劳微裂纹、不完美界面等)所引起的声学非线性效应。大量研究者针对此类问题进行了深入的研究。Qian[17]深入研究了P波、SV波和SH波斜入射情况下的二阶声场，利用势函数的表示方法对二维声波方程进行详细求解。一些研究者基于二维非线性方程探究非线性纵波的斜入射的问题。Biwa等[18]建立固-固界面的弹簧模型，对声波斜入射情况下的二阶声场特性进行详细研究。Shirgina等[19]针对四种不同类型的界面层，探究斜入射纵波产生的非线性谐波的反射传播特性。Wu等[20]基于钱祖文的研究对P波斜入射于固-固界面的二阶谐波场特性进行了详细描述。声波在有微小缺陷的固体材料中传播，所产生的非线性现象是由固体介质的材料特性和固体微小缺陷共同贡献的。上述研究者在研究固-固界面的非线性问题时，重点关注声波在固体介质中传播时由固体缺陷产生的非线性现象。而在此基础上进一步考虑声波与固体材料相互作用而产生的非线性影响，可以得到更加精确的结果。相关内容还未在相关文献中呈现，这对于固体中的非线性超声评估研究而言仍是一个值得关注与研究的问题。因此，有必要对二维固体中非线性弹性波的特性进行相应研究，即研究二维非线性声波方程的非线性问题。

Alkhalifah[21]利用纵波方程代替弹性波方程，并将微扰理论应用于求解各向异性的纵波方程中，以描述纵波斜入射所产生的纵波场。该方法通过引入一个远小于1的无量纲小参数作为摄动量，采用泰勒展开的方式对方程的解进行微扰展开，最终得到相应的解析解。基于上述研究方法，本文选取声马赫数作为微扰小项，围绕其对二维非线性声波方程的解进行摄动求解。

本文从二维非线性纵波方程出发，围绕声马赫数对该方程的解进行二阶摄动展开，从而求解出二维非线性纵波方程的二阶摄动解。考虑到在实际测量情况下，单个探头单次只能测量某一方向的声波信号。因此，根据计算结果定义了两个非线性系数(二次谐波沿x轴传播分量A1x和沿y轴传播分量A1y与入射基波A0的振幅比)，利用数值计算的方法探究影响非线性系数的因素，从而探寻二维非线性纵波及其二次谐波的传播规律。

1 二维纵波非线性方程的摄动解

为探究某一特定方向上二维纵波传播时的非线性，对其沿坐标轴进行了相应分解。建立如图 1所示的声波传播模型，二维纵波在具有各向同性的固体材料中传播。

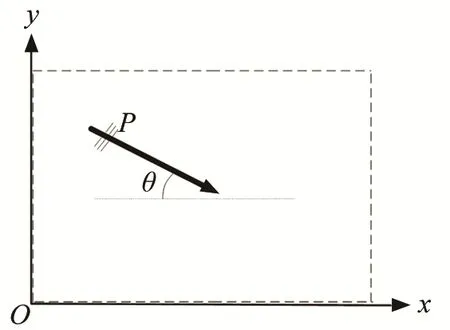
图1 二维纵波在固体介质中传播的示意图Fig.1 Two-dimensional longitudinal wave propagation in solid media

图1中，虚线所围成的长方形表示固体介质。二维纵波P以入射角θ斜入射于固体材料，并在固体中传播。当θ=0°时，表示二维纵波沿x轴方向入射，当θ=90°时，表示二维纵波沿y轴方向入射。

根据Murnaghan参数[3]推导的固体中的二维纵波方程，如式(1)、(2)所示：

其中， u = u ( x, y, t )和v= v ( x, y, t)分别表示二维纵波沿x轴方向传播的位移分量和沿y轴方向传播的位移分量；ρ0为固体材料的密度；λ、μ为 Lame常数；l、m为Murnaghan参数。

摄动法是求解非线性方程近似解的常用方法之一。其主要思想是将方程中的非线性因素视为对方程中线性部分的一种微小扰动，基于线性解寻求方程的近似解。在利用摄动法求解方程的过程中常常需要引入与方程中物理量相关的无量纲小参数作为摄动量，且其值应远小于 1。因此，本文选取声马赫数Ma作为摄动小项，Ma的计算公式为

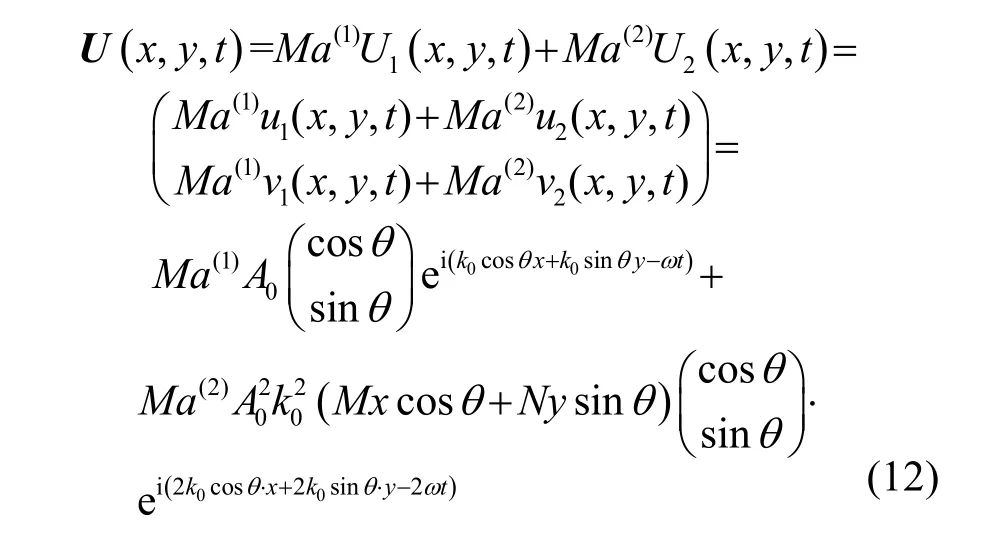
最终得到的式(12)即为二维纵波非线性波动方程(1)和(2)的摄动解。

2 数值计算与结果分析

根据式(12)中的二维纵波非线性方程的摄动解可知，二维纵波在固体中传播时，其传播特性不仅会随传播距离变化，也受入射角度的影响。从角频率成分来看，式(12)出现了角频率为2ω的谐波分量，即为二次谐波。研究者常将二次谐波振幅与入射基波振幅的比值定义为非线性系数，从而进行研究[6]。因此，分别定义二次谐波沿x轴传播分量的振幅A1x和沿y轴传播分量的振幅A1y与入射基波的振幅A0之比的绝对值为非线性系数：

为研究二维非线性纵波在固体中传播时产生的二次谐波的传播特性，应用式(13)和式(14)，通过数值计算模拟非线性系数随声传播距离和入射角的变化。其中材料参数选自文献[22]，如表1所示。

表1 某钢轨样品的二阶和三阶弹性常数Table 1 The second and third order elastic constants of a rail sample

图 2为在入射波振幅为 1 μm，入射频率为1 MHz时，不同入射角度下，非线性系数与声传播距离的关系图。图注中x表示二维纵波沿x轴传播的位移分量，y表示二维纵波沿y轴传播的位移分量。从图2(a)中可以看出，随着入射角的增大，非线性系数呈减小的趋势。入射角为0°时，即垂直入射的情况，此时非线性效应最为明显；入射角为 0°～30°时，非线性系数较大，说明此时非线性效应较为明显；入射角为30°～60°时，非线性系数迅速减小；入射角大于 60°时，非线性系数趋于平稳，此时非线性效应较小；入射角为 90°时，即水平入射的情况，此时二次谐波沿y轴方向传播，可认为沿x轴方向不存在非线性效应。

从图 2(a)、2(b)中可以看出，随着二维纵波在固体中传播距离的增加，非线性系数和均逐渐增大，且随着传播距离的增加，非线性系数变化更明显。这是由于声波在固体中传播时，会产生不同频率的高次谐波，各阶次谐波间会产生相互的影响，随着声传播距离的增加，非线性效应积累增多，其非线性现象会更为明显。

图2 不同声传播距离的非线性系数|A1x/ A0|和|A1y/A0|与入射角关系图Fig.2 Relationships of nonlinear parameters|A1x/ A0| and |A1y/A0|with incident angle at different sound propagation distances

为研究二维纵波在固体中传播时，其入射振幅对非线性系数|A1x/A0|和 |A1y/A0|的影响，入射振幅A0依次取1、2、3、4、5 μm进行数值分析。

图3为入射频率为1 MHz时，不同入射角度下，非线性系数与入射振幅的关系图。从图3(a)和3(b)中可以看出，随着入射振幅的增大，非线性系数逐渐增大，且入射角越小，非线性系数变化越明显。这说明了振幅大的二维纵波在固体中传播时，其声扰动更强，声波的非线性效应也更为显著。

根据图2中非线性系数与入射角的变化关系可知，选取入射角为 30°、45°和 60°的情况，可以很好地描述非线性系数的变化情况。从图3(c)和3(d)中可以发现非线性系数与入射振幅呈正比例关系，且入射角越大，图 3(c)中所对应的直线的斜率越大；图3(d)中所对应的直线的斜率越小。

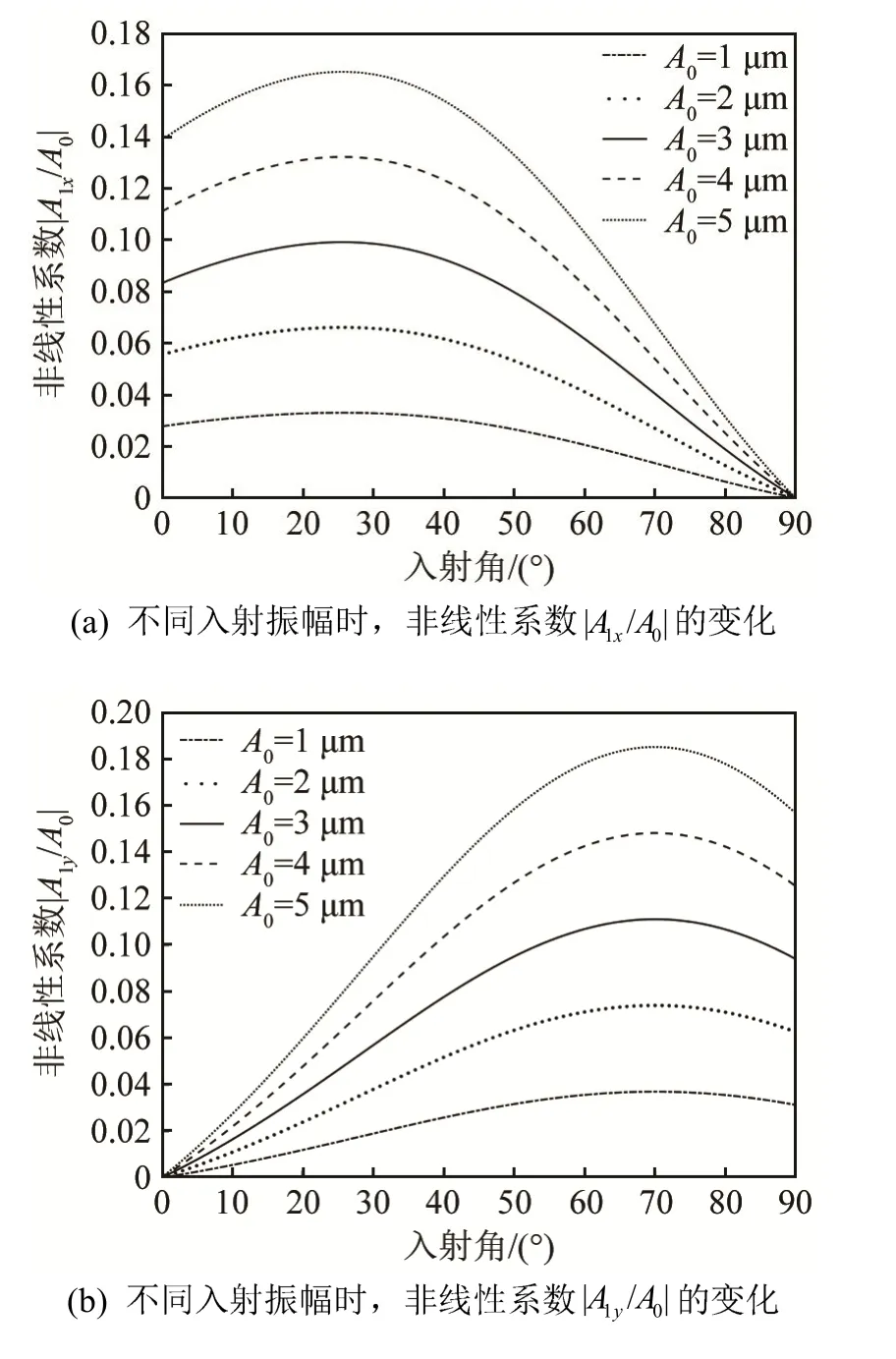
图3 非线性系数|A 1x / A0|和 |A 1y/A0|与不同入射角及入射波振幅A0的关系图Fig.3 Relationships of nonlinear parameters |A 1x/ A0| and |A 1y/A0|with incident angle and the amplitude A0 of incident wave

为研究二维纵波在固体中传播时，其入射波频率对非线性系数|A1x/A0|和|A1y/A0|的影响，入射波频率取1、2、3、4、5 MHz进行数值分析。

图4为入射振幅为1 μm时，不同入射角度下，非线性系数与入射频率的关系图。从图4(a)和4(b)中可以看出，随着入射频率的增大，非线性系数逐渐增大，且入射角越小，非线性系数变化越明显。这说明了入射纵波的频率越大，其在波列中的质点单位时间内振动次数越多，即声扰动更强。此时，二维纵波在固体中传播所产生的非线性效应更为显著。图 4(c)和 4(d)选取了入射角 30°、45°和 60°的情况进行分析，可以发现非线性系数与入射频率呈正相关，且入射角越大，图4(c)中所对应的曲线递增得越慢，即非线性效应越小；图4(d)中所对应的曲线递增得越快，即非线性效应越显著。

图4 非线性系数|A 1x/A0|和|A 1y/A0|与不同入射角及入射波频率f的关系图Fig.4 Relationships of nonlinear parameters|A 1x/A0|and|A1y/A0|with incident angle and the frequency f of incident wave

3 结 论

本文从二维纵波非线性方程出发，围绕声马赫数对该方程的解进行二阶摄动展开，从而求解出二维纵波非线性方程的二阶摄动解。根据计算结果定义了非线性系数|A1x/A0|和 |A1y/A0|(二次谐波沿 x轴传播分量和沿y轴传播分量与入射基波的振幅比)，并探究二维纵波在固体中传播时其入射振幅、入射频率、入射角以及声传播距离对非线性系数的影响。结果表明，非线性系数|A1x/A0|和|A1y/A0|与入射角有关，且垂直入射时非线性效应最为显著；同时，二维纵波在固体中的声传播距离、入射振幅和入射频率也是影响非线性系数|A1x/A0|和|A1y/A0|数值变化的因素。上述非线性系数可以用于描述二维纵波与二次谐波的传播规律，并用于定性分析固体材料的非线性。为后续在固-固界面的研究基础上进一步考虑固体材料的非线性的研究提供理论支持。

附录Ⅰ