多输出回归算法在超声粒径分布反演中的研究

应启帆，谢代梁，徐志鹏，徐 雅，刘铁军，黄震威

(中国计量大学浙江省流量计量技术研究重点实验室，浙江 杭州 310018)

0 引 言

水体悬移质粒径分布测量在河流、湖泊、海洋和生态系统等领域中有着重要价值，其准确测量有助于认识悬移质沉降、扩散规律[1]，对水土流失规律研究[2]和水污染治理[3]等领域的发展有重大意义。

粒径测量方法按照工作原理[4]，可分为筛分法、显微镜法、沉降法、光散射法和超声法等。其中，超声法测量具有非浸入式、穿透性强、操作简单等优点，受到了广泛关注。Shukla等[5]使用超声波谱在线监测乙酰氨基酚结晶过程中的颗粒生长；章维等使用超声波衰减谱和相速度谱及Epstein-Carhart-Allegra-Hawley (ECAH)模型反演计算悬浊液颗粒粒径分布[6]；Ding等[7]使用超声频谱测量了水分散体系中重油的粒径；李烨明等采用人工蜂群算法优化超声粒径分布计算结果[8]。

对粒径分布的测量，传统学者多聚焦在选用更精准的模型和更加优化的算法来提升粒径分布结果的准确度。苏明旭等[9]通过构造与贝塞尔(Bessel)函数有关的变量改造系数矩阵，降低了矩阵求解的条件数，拓展了模型适用的频率和颗粒粒径。Silva等[10]使用 6～14 MHz频率光谱法和扩展多重散射模型测量体积分数为10%～50%的葵花籽油包水型乳液的液滴尺寸分布。由于机器学习的发展和测量数据的提升，有学者尝试用数据来寻找颗粒粒径分布和输入特征之间的关系，通过训练机器学习模型来进行预测。Thompson等[11]利用基因表达编程和人工神经网络开发了一种新模型，用于预测活跃施工现场和露天采矿作业中裸露的土壤表面产生的雨水径流中的总悬浮泥沙粒径分布；Schäfer等[12]使用卷积神经网络和人工图像进行训练，通过分割重叠颗粒来预测多相流中液滴的粒径分布；Manee等[13]提出了一种深度学习传感器，可对晶体生长过程中的颗粒进行在线监测。

在本文中，我们提出了一种结合多输出回归算法和超声衰减实验的粒径分布测量方法。首先根据超声衰减实验和 ECAH模型等先验信息获取实验信号并提取特征，然后利用梯度提升决策树算法预测单种粒径，并组合全部粒径预测模型构建多输出回归模型预测样品的粒径分布。最后将近似单峰分布、均匀分布和不规则分布的三种样品粒径分布预测结果与筛分法确定的粒径分布进行对比，验证多输出回归模型的准确性，可为粒径分布测量提供一种新的参考方式。

1 基本理论

超声法测量颗粒粒径主要根据理论模型和优化算法来获得结果。理论模型介绍了超声波在不同粒径颗粒液体中的衰减情况，也成为了在机器学习算法中的特征基础。接下来主要介绍 ECAH模型和超声衰减实验，了解粒径测量的过程。

1.1 ECAH模型

ECAH模型说明了超声波在水体中受到的粘滞力、热损失和声散射等因素的影响，可以描述超声波具体的衰减过程。它忽略了颗粒之间的相互作用，适用于5%体积浓度以下、粒径在1 000 um以下的悬移质溶液环境，具体说明如式(1)[14-15]所示：

式中：α为超声波在水中的衰减系数(单位：Np·m-1)；kc为连续介质中的波数；φ为悬移质溶液体积浓度，(单位：g·L-1)；R为悬移质颗粒半径(单位：μm)；An为悬移质溶液中的超声衰减系数，不同的下标n代表不同种衰减情况。

颗粒粒径的求解过程是第一类 Fredholm 方程计算问题，可利用超声衰减系数、浓度等参数之间的相关关系来求解，是典型的反问题，参数关系如式(2)[16]所示：

式中：q是颗粒粒度的频度分数，是要求解的结果；K是消声系数，是关于频率和粒径区间的函数。

通过对式(2)的离散化处理，可以转化成矩阵形式来求解[16]：

式中： fi为不同测量频率(单位：kHz)；Rj为不同粒径区间(单位：Np·m-1)；α( fi, Rj)为在特定频率和特定粒径区间时的衰减系数(单位：Np·m-1)。

等式左边是声衰减过程，是超声波在不同频率和粒径里的衰减过程，通过实验获得。等式右边是理论部分，可以结合ECAH模型和各项物性参数来进行求解。式(1)～(3)描述了采用 ECAH模型求解颗粒粒径分布的过程，是先验信息。后续的特征部分就是根据这部分理论来选取与超声衰减过程密切的相关参数作为数据集的输入。

1.2 超声衰减实验

超声衰减实验采用两个聚焦换能器进行声电信号转换，通过一发一收的工作方式，对电压幅值进行测量，可探测到超声波在悬移质溶液中的衰减过程。聚焦换能器采用的材料为压电材料PZT82；球面内径为 100 mm；投影直径为 90 mm，换能器中心频率为 750 kHz，单个聚焦换能器具体的结构如图1所示。

图1 超声换能器结构Fig.1 Ultrasonic transducer structure

发射换能器接收信号发生器的电信号，将其转化成声信号发射，声信号在穿过悬移质溶液后到达接收换能器。在这个过程中超声波会发生反射，从而多次到达接收换能器，采用示波器测量接收换能器提供的电压信号，就可看出超声波衰减过程，具体的测量装置如图2所示。

图2 超声测量装置Fig.2 Ultrasonic measuring device

2 多输出回归算法

粒径分布反演问题在机器学习中的表现是多输入多输出回归问题，根据多个输入找到对应的多个目标预测结果。本文采用组合梯度提升决策树(Gradient Boosting Decision Tree, GBDT)算法来解决这一问题。首先利用 GBDT算法来找到单种粒径的回归预测结果，然后将所有GBDT算法组合起来，对整体粒径分布进行预测。

2.1 梯度提升决策树

梯度提升决策树是一种集成学习算法，算法的基础是分类回归决策树，利用损失函数的梯度方向决定后续回归树的优化方向，通过贪心算法每一次找到下一步更优的回归树，最后对所有回归树进行集成，输出最后结果，就构成了梯度提升决策树模型。算法训练[17]的步骤如下所示：

算法每次对负梯度和输入特征进行拟合，构建新的回归树来修正模型，其问题类型是多输入单输出的回归预测模型，因此不适用于粒径分布问题，只适用于单种粒径分布的预测，需要将多个GBDT模型进行组合来解决问题。

2.2 GBDT回归组合

对每种粒径，单独训练一个GBDT模型，可以根据输入特征和粒径的数值进行回归预测。为了预测样品的粒径分布，需要所有模型组合，每个输出对应粒径的结果，最后按照对整体粒径的权重确定整体粒径的频度分布，多输出回归模型示意图如图3所示。

图3 多输出回归模型示意图Fig.3 Diagram of the multi-output regression model

3 特征选取

3.1 实验信号

为了获得实验信号提取特征来制作数据集，搭建了如图4所示的实验测试系统。首先接收端聚焦换能器接收功率放大器放大的猝发波信号。超声信号到达接收换能器时部分转换成电压幅值，部分反射回接收聚焦换能器。最后呈现在示波器上的是超声波到达接收端聚焦换能器时的电压幅值，最终将数据读取并存储在电脑中。实验器材：发射和接收聚焦换能器、功率放大器、信号发生器、电磁搅拌器和示波器。

图4 实验系统Fig.4 Experimental system

实验获得的电压信号经去噪后的波形如图5所示。同时考虑到换能器中心频率的影响，提取其在频域下的幅值，如图6所示。

图5 去噪后接收信号波形图Fig.5 Waveforms of the received signals after denoising

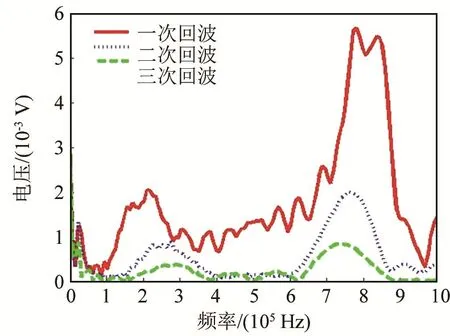
图6 去噪后接收信号频谱图Fig.6 Spectrums of the received signals after denoising

图5中三个回波表示超声波三次到达接收聚焦换能器时的电压幅值，声衰减系数就可通过这三个峰峰值计算而出，如式(7)[8]所示：

式中：αw为清水中的衰减系数(单位：Np·m-1)；V0是发射换能器电压幅值(单位：V)，V1为接收换能器电压幅值(单位：V)；L为两个聚焦换能器之间的距离(单位：m)。

3.2 特征选取

多输出回归模型的特征来源于先验信息，即颗粒的 ECAH模型和超声衰减实验的信号特征。接下来以各个参数与粒径之间的关系来说明选择它作为特征的理由。

根据ECAH模型反演来看，式(1)说明了粒径与超声衰减系数和体积浓度之间的关系，由图5中的三次回波可计算出两个衰减系数，因此将两个声衰减系数和体积浓度作为特征。式(3)说明了频率可以影响声衰减系数的计算，同时考虑到超声换能器中心频率对信号的影响，在选择特征时加入频率这一参数。

图5说明了声衰减变化的电压衰减过程。图6说明了图5中三次回波在各频率下的幅值，结果表明在中心频率附近的傅里叶变换后幅值最大。三次回波的电压峰峰值和三次回波的傅里叶变换最大幅值，是超声衰减的关键因素，因此也选择其作为特征。

综上所述，选择了悬移质溶液体积浓度、两次声衰减系数、频率、三个电压峰峰值幅值和三次回波傅里叶变换后的最大幅值共 10个属性作为数据集的特征，具体说明如表1所示。

表1 数据集输入特征Table 1 Input features of data

为了避免特征数据量纲不同导致在回归树预测时带来的偏差，需要对数据进行预处理。对特征为种类的频率进行 onehot编码，将 660、750、830 kHz三种频率转化为数值1、2、3；对其他连续数据进行标准化处理，将数据映射到[0,1]，转换公式如式(8)[18]所示：

式中：x*是数据组中数据的转换结果，x是数据组中数据初始值，xmin是数据组中数据最小值，xmax是数据组中数据最大值。

4 结果分析

4.1 数据集组成

本文的样品通过筛分法进行配置，即先通过孔筛筛选出在各个粒径区间范围内的颗粒粒径，然后由精密天平称重组合成近似各种分布类型的悬移质样品。以对照组的三种悬移质样本为例进行说明，三个样本分别服从近似单峰分布、均匀分布和不规则分布，粒径区间有 17种。单种粒径区间质量占样本总质量的百分比为该种粒径区间的频度，将 17种粒径区间频度进行组合，就构成了样本的粒径分布，具体的粒径组成如表2所示。

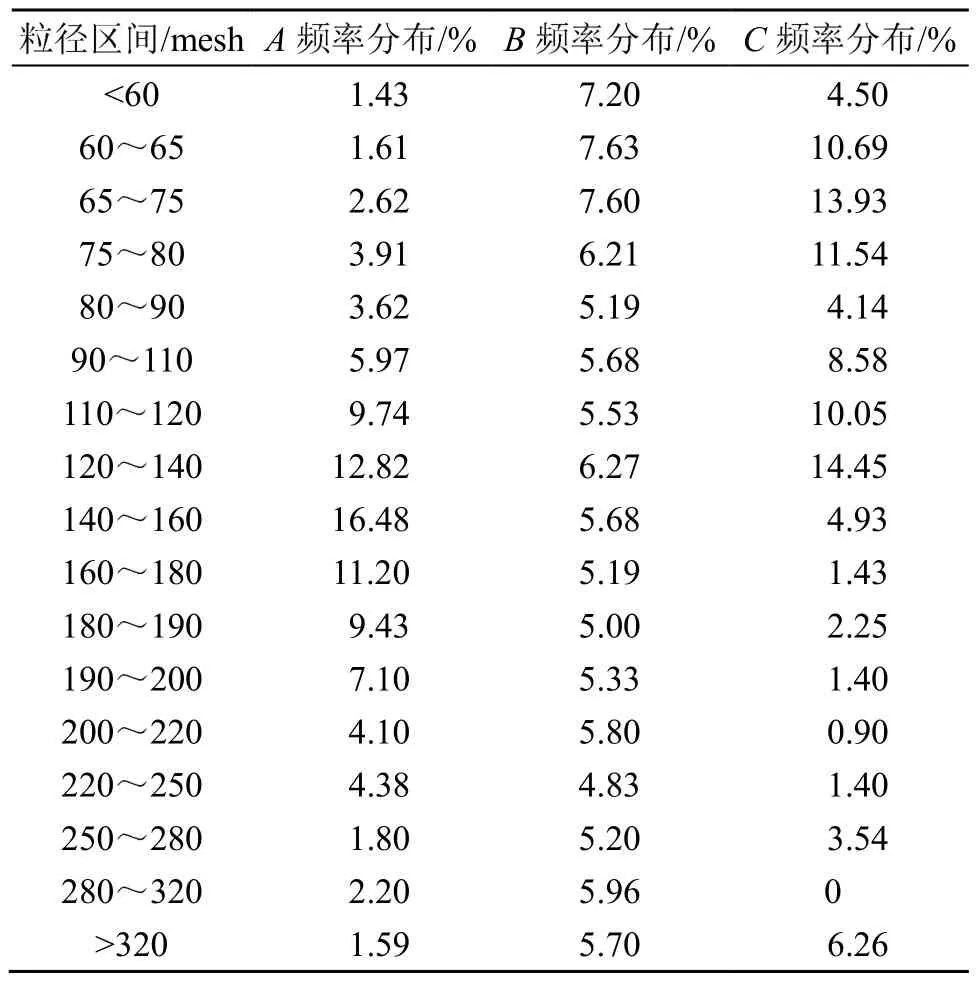
表2 悬移质颗粒样品粒径分布组成Table 2 Composition of the particle size distribution of suspended particles

本次实验共配置了36组实验样品，其中33组用于制作训练数据集，其余3组用于制作验证数据集。对所有样品进行三种频率下的超声衰减实验，然后针对每一次实验分别提取 10项特征作为数据集的输入，并且将 17种粒径分布的值作为数据集的输出。

本文将训练数据集用于训练多输出回归模型，同时将验证数据集输入模型，即可得到粒径分布预测结果。因为考虑到有三种频率下的实验，所以为了得到更加精确的结果，对三次预测结果进行均值化处理，作为真正的粒径分布结果。

4.2 预测结果和误差分析

中位径D50代表一个样品的累计粒度分布百分数达到50%时所对应的粒径，中位径误差ε是常用的粒径误差计算公式，如式(9)[19]所示：

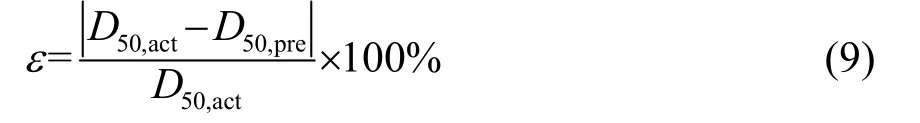
式中：D50,act为实际的中位径(单位：μm)；D50,pre是模型预测确定的中位径(单位：μm)。

首先利用训练数据集训练多输出回归模型，然后利用验证数据集和模型预测三种样品的粒径分布结果。预测得到的单峰分布、均匀分布和不规则分布样品筛分结果和多输出回归模型预测结果对比图分别如图7～9所示。

图 7～9的横坐标是粒径区间的组合，柱状图分别为筛分法确定的该种粒径频率分布和模型预测的粒径频率分布，纵坐标为粒径的频率分布，即单种粒径区间质量占样品质量的百分比。所有粒径的结果进行组合就构成了样本粒径分布的结果。接下来统计了每种样品的单个粒径的最大相对误差、决定系数和中位径误差，如表3所示。

表3 不同样本中位径和测量误差Table 3 Median diameters and measurement errors of different samples

图7 单峰分布样品两种方法测量结果对比Fig.7 Comparison of measurement results of two methods for unimodal samples

三种样品的单种颗粒相对误差范围都在±10%以内，只有单峰分布的个别样本在粒径权重较小时出现了较大的偏差，为 12.74%。这表明，单种粒径占总体粒径分布的权重质量较小时会导致相对较大的偏差。中位径的误差都较小，表明预测分布与实际分布较为一致，可以很好地反应悬移质颗粒粒径分布组成。

图8 均匀分布样品两种方法测量结果对比Fig.8 Comparison of measurement results of two methods for uniformly distributed samples

图9 不规则分布样品两种方法测量结果对比Fig.9 Comparison of measurement results of two methods for irregularly distributed samples

5 结 论

本文通过 ECAH模型和超声衰减实验等先验信息，了解传统粒径分布测量的过程，并说明了颗粒粒径与体积浓度、声衰减系数之间存在的耦合关系，使用机器学习算法对粒径分布进行预测来为粒径分布测量提供一种新的方法。

粒径分布预测作为一种多输入多输出回归问题，采用组合梯度提升决策树来进行预测。首先使用 GBDT对单种粒径进行预测，然后组合所有粒径预测过程，就构成了对粒径分布结果的预测。然后选择了与粒径关系密切的体积浓度、二次声衰减系数和超声衰减实验中最明显的三次回波电压峰峰值和傅里叶变换最大幅值共 10项参数作为数据集的特征。最后，采用近似单峰分布、均匀分布和不规则分布的三种样品作为预测结果，三种样品中单种粒径相对误差范围在±10%以内，中位径误差分别为0.07%、-0.1%和-2.2%，表明预测样品结果与实际样品结果较为一致，可以很好地测量样品的粒径分布。

本文利用的特征根据先验信息进行选取，也可以进一步通过对超声信号的分解来选取与粒径关系密切的特征来进行训练。同时，使用更大规模的数据集来进行训练，可得到某个区域更准确的粒径分布结果。本文的尝试，可以为粒径分布测量问题提供一种新的思路。