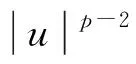一类带对数非线性项的分数阶伪抛物方程的存在性与爆破
2022-03-11王冬秀邓启刚曾福庚
王冬秀,邓启刚,曾福庚
(贵州民族大学 数据科学与信息工程学院,贵阳 550025)
考虑如下一类带对数非线性项的分数阶伪抛物方程的初边值问题:
(1)

方程(1)在自然科学中有广泛应用,尤其可应用到一些物理、生物场景.比如非线性、色散、长波的单向传播[1],种群聚集[2]和晶体半导体中的非平稳过程[3]等.
当s趋向于1时,方程(1)变为标准的拉普拉斯方程:
(2)
围绕方程(2)解的性质研究通常采用由Sattinger[4]、Payn和Sattinger[5]建立的位势阱法以及一些改进的位势阱理论[6].Chen和Tian[7]给出了关于方程(2)解的最新理论,证明了全局存在性和无穷远处爆破等系列结果.对于其他结果,可参见文献[8-11].
在分数阶情形下,Nezza等[12]在索伯列夫(Soblev)空间上建立了相应的Sobolev不等式和Poincare不等式.Fu和Pucci[13]研究了方程:
(3)
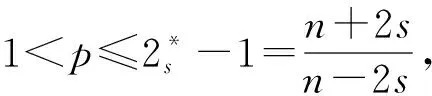
(4)
并得到了方程(4)在初始能量J(u0)≤d时解的全局存在性、衰减性以及在无穷时间的爆破.
1 预备知识
首先回顾分数阶Soblev空间的一些定义和性质[12].
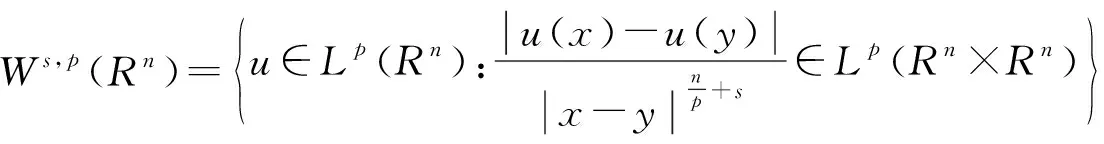
注1当p=2时,Ws,2(Rn):=Hs(Rn)是Hilbert空间.

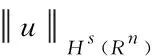
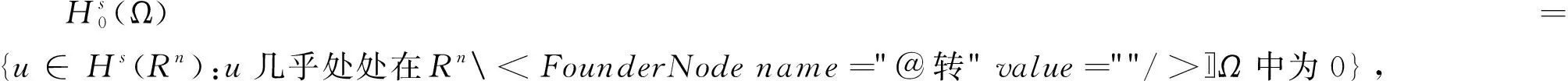
定义能量泛函J(u)和Nehari泛函I(u)如下,
(5)
(6)
由引理1有
(7)
由式(5)(6)和(7),可得
(8)
(9)
紧接着定义位势阱集
(10)
并且给出位势阱集相对应的集合为
(11)
其中d为位势阱深度,

(12)
给出Neheri流形为
(13)
通过式(8)和式(9)有
(14)
下面给出弱解、最大存在时间、有限时间爆破的定义.
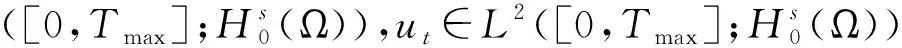

(15)
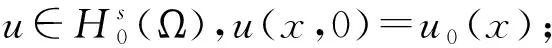
(iii) 对于0≤t (16) 定义3(最大存在时间) 设u=u(x,t)是方程(1)中的解,最大存在时间定义为 (i) 如果u(x,t)存在区间为[0,∞),则Tmax=+∞; (ii) 如果存在t0∈[0,∞),使得u(x,t)在0 (17) (18) 由式(18)有J(um(0))→J(u0).对于足够大的m和J(u0) (19) 由式(18)和J(u0) 因此,对于足够大的m和0≤t≤T0有 um(x,t)∈W. (20) 由式(14)(19)和(20)有 (21) 对于足够大的m和0≤t≤T0,即 (22) (23) (24) 由式(22)可得T0=+∞. (25) umt⇀ut在L2([0,∞);L2(Ω))中弱收敛. (26) 由式(25)(26)和Aubin-Lions-Simon引理[16]有 um→u在C([0,∞);L2(Ω))中强收敛. 因此, (27) (28) 由式(27)(28)可得 (29) 根据式(25)(26)和(29),在(17)中取极限m→+∞,则对a.e.t∈(0,+∞)有 (30) 对式(30)从0到t积分有 (31) 类似地,对式(17)从0到t积分,然后取极限m→+∞有 (32) 由式(31)(32)可得u(0)=u0.令θ(t)∈C([0,T])是非负函数,则有 (33) 因此有 因为θ(t)是任意的,则有 证明由反证法,不妨设方程(1)具有全局解u(t),最大存在时间Tmax=+∞.定义 (34) 则有 (35) (36) 由式(36)有 (37) 根据式(15)(16)可得 (38) 因为J(u0) 由引理2,∃λ*∈(0,1),使得I(λ*u)=0,通过d的定义,可以推出 (39) 由式(38)(39),可得 (40) 结合(37)和I(u)<0有G″(t)>0,所以, (41) 由式(36)和Holder不等式,有 (42) 结合(34)(40)和(42),得到 (43) 现在固定t0>0,那么由式(39)有 (44) 因此, (45) 取T>t0足够大,定义 (46) 那么,M(t)≥G(t)>0,M′(t)=G′(t)-G′(0)且G″(t)=M″(t)>0,则由式(42)可得, (47) (48) (49)
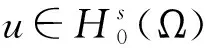
2 主要结果和证明
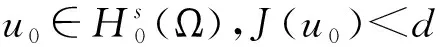
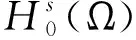

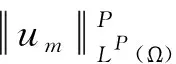
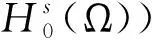
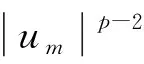
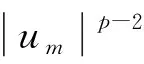
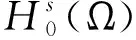
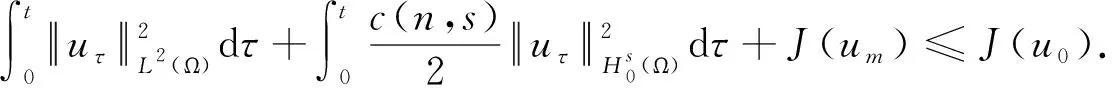
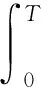

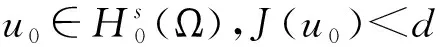
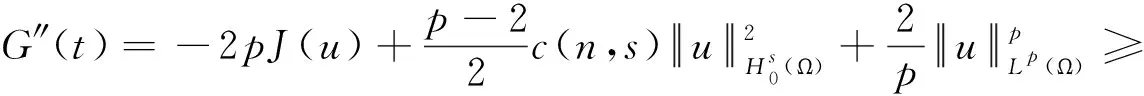
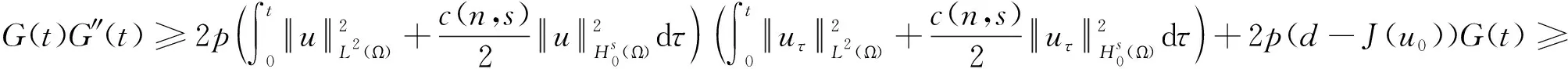
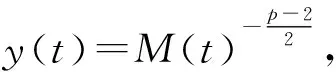

3 结语