m-几何凸函数的Hermite-Hadamard型积分不等式
2022-03-11王淑红
刘 倩,王淑红
(内蒙古民族大学 数理学院,内蒙古 通辽 028000)
凸函数是一个简单而自然的概念,在工业、商业、 医学和艺术中均有大量应用.但遗憾的是涉及实际问题中的大量函数都是非凸函数.这就促使人们考虑有别于通常凸性的其他形式的凸性,如拟凸函数、s-凸函数、预不变凸函数、p-凸函数、h-凸函数等,这些统称为广义凸函数,使其既能保持凸函数的一些良好性质又具有比凸性更弱的条件,其实用的范围却比凸函数要广.Toader[1]引入了m-凸函数的概念,并研究了m-凸函数的基本性质.Dragomir[2]建立了m-凸函数的Hermite-Hadamard类不等式.Zhang等[3]引入了几何凸函数和s-几何凸函数的概念,并建立了一些几何凸函数和s-几何凸函数的Hermite-Hadamard类不等式.Tunç[4]建立了几何凸函数和s-几何凸函数的Hermite-Hadamard类积分不等式.Xi等[5]定义了m-几何凸函数和(α,m)-几何凸函数,并建立了一阶可微单调递减m-几何凸函数和(α,m)-几何凸函数的Hermite-Hadamard类不等式.Önalan等[6]建立了m-几何凸函数和(α,m)-几何凸函数的Simpson类不等式.Tunç[7]建立了m-几何凸函数和(α,m)-几何凸函数的Ostrowsk类Riemann-Louville分数积分不等式.Baloch等[8]建立了调和(s,m)凸函数的Fejér类不等式.Bracamonte等[9]建立了第二种意义下互(s,m)-凸函数的一些不等式.在此基础上,本文继续研究m-几何凸函数,建立了一些新的基于区间[a,b]上m-几何凸函数的积分均值、区间[a,b]端点几何均值的像和区间[a,b]端点像的几何均值的Hermite-Hadamard类不等式.
1 预备知识
首先给出经典凸函数的概念:
定义1[10-11]设f:I⊆R=(-∞,∞)→R,如果f满足
f(tx+(1-t)y)≤tf(x)+(1-t)f(y),
其中x,y∈I,t∈[0,1],则称f(x)是I上的凸函数.
下面的双不等式就是著名的Hermite-Hadamard积分不等式.
定理1[12-13]设f:I∈R→R是一个定义在实区间I上的凸函数,a,b∈I且a 1985年,Toader引入了m-凸函数的概念. 定义2[1]设f:[0,b]⊂R→R,m∈(0,1],如果 f(tx+m(1-t)y)≤tf(x)+m(1-t)f(y), 其中x,y∈[0,b],t∈[0,1],则称f(x)是[0,b]上的m-凸函数. 2002年,Dragomir给出了m-凸函数的Hermite-Hadamard型积分不等式. 定理2[2]设f:[0,∞)→R是一个m-凸函数,0≤a 2012年,Zhang等人引入了几何凸函数. 定义3[3]设f:I⊂R+=(0,+∞)→R+,如果 f(xty1-t)≤[f(x)]t[f(y)]1-t, 其中x,y∈I,t∈[0,1],则称f(x)是I上的几何凸函数. 2012年,Tunç给出了几何凸函数的Hermite-Hadamard类积分不等式. 定理3[4]设f:I⊂R+→R+是一个定义在I上几何凸函数.若f在区间[a,b]⊂I上是单调递减的,则 2012年,Xi等人给出了m-几何凸函数的概念,并建立了m-几何凸函数的Hermite-Hadamard类积分不等式. 定义4[5]设f是[0,b]上的正值函数,t∈(0,1],如果 f(xtym(1-t))≤[f(x)]t[f(y)]m(1-t), 其中x,y∈[0,b],m∈[0,1],则称f(x)是[0,b]上的m-几何凸函数. 定理4[5]设f:I⊂[0,∞)→(0,∞)是可微函数.若f′∈L([a,b]),且|f′(x)|在区间[min{1,a},b]上是单调递减的m-几何凸函数,0≤a 为了方便起见,引入记号W0(x)=f(x),Wi(x)=fmi(xm-i),(i=1,2).对数均值L(u,v): (1) 定理5设f:I⊆R+→R+是一个可积函数,a,b∈I且a (2) 其中G(u,v)是几何均值,L(u,v)是对数均值. 证明由f的m-几何凸性有 (3) 取x=atb1-t,y=a1-tbt,代入式(3)有 (4) 将式(4)在区间[0,1]上对t积分,即得式(2)的左边不等式. 再次利用f的m-几何凸性,有 (5) 将式(5)在区间[0,1]上对t积分,即得式(2)的右边不等式. 定理6设f:I⊆R+→R+是一个可积函数,a,b∈I且a A(G(W1(b),L(W2(a),W0(a))),G(W1(a),L(W2(b),W0(b))))≤ (6) 其中A(u,v)是算术均值,G(u,v)是几何均值,L(u,v)是对数均值. 证明在式(3)中分别取x=atb1-t,y=a1-tbt和x=a1-tbt,y=atb1-t得 求和得 (7) 将式(7)在区间[0,1]上对t积分,即得式(6)中的第一个不等式. 类似式(5)的讨论,有 (8) 对式(5)和式(8)在[0,1]上对t积分,再利用式(7)即得式(6)中的第二个不等式.利用均方值不等式也得到式(6)的第三个不等式. 定理7设f:I⊆R+→R+是一个可积函数,a,b∈I且a (9) 其中A(u,v)是算数均值,G(u,v)是几何均值,L(u,v)是对数均值. 证明利用函数f的m-几何凸性和均值不等式,得 (10) 将式(10)中第二个不等式在区间[0,1]上对t积分,即得式(9)中的第一个不等式. 再将式(10)中第三个不等式在区间[0,1]上对t积分,即得式(9)中的第二个不等式. 定理8设f:I⊆R+→R+是一个可积函数,a,b∈I且a A(L(bW1(b),aW0(a)),L(aW2(a),bW1(b))), (11) 其中A(u,v)是算术均值,G(u,v)是几何均值,L(u,v)是对数均值. 证明类似定理7的讨论,得到: 和 A(L(bW1(b),aW0(a)),L(aW2(a),bW1(b))). 本文利用经典的均值不等式和m-几何凸函数的概念,建立了一些新的基于区间[a,b]上m-几何凸函数的积分均值、区间[a,b]端点几何均值的像和区间[a,b]端点像的几何均值的Hermite-Hadamard类不等式.关于m-几何凸函数以及(α,m)-几何凸函数的性质和应用还有待进一步讨论.

2 主要结论


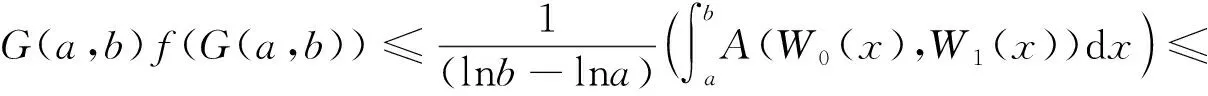
3 结语
