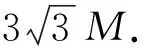Horava-Lifshitz黑洞时空中的测地线结构

唐睿君,李 倩,刘显明

(1.湖北民族大学 数学与统计学院，湖北 恩施 445000；2.湖北民族大学 信息工程学院，湖北 恩施 445000)

GW150914引力波事件[1]、事件视界望远镜对M87黑洞阴影图像的描绘[2]有力支持了爱因斯坦广义相对论的正确性.然而，众所周知广义相对论理论存在紫外发散、不可重整化，带来了引力量子化的困难，这一直是困扰理论物理学家的重大难题.最近，Horava提出了一种非相对论性可重整化的量子引力理论——Horava-Lifshitz(HL)引力理论，该理论在红外尺度上能回到广义相对论，在紫外尺度上通过破坏洛伦兹对称性来建立一个紫外(ultraviolet)完备理论[3-4].该理论目前已经在宇宙学和黑洞物理中得到广泛地应用[5-10].

在强引力场中研究测地线的结构能够探测致密天体的物理特征，这一直是物理学与天文学领域的热点问题[11-17].应用有效势的方法可以方便地研究黑洞的测地线结构.近年来，Hu等[14]通过有效势的方法讨论规则Hayward黑洞时空中的类时测地线和类光测地线.Enolskii等[18]也研究了HL引力下渐进平直时空中的黑洞[19]中的粒子运动.

本文将应用有效势的方法详尽地讨论HL黑洞时空中的类时和类光测地线结构，着重关注HL黑洞时空中的参数ω对类时测地线中不稳定圆轨道、稳定圆轨道、最小半径束缚轨道以及类光测地线中不稳定圆轨道、HL黑洞阴影半径的影响.

1 Horava-Lifshitz(HL)黑洞时空下测地线结构

1.1 轨道运动方程与有效势

渐近平直时空背景中的HL黑洞的线元为[19]

(1)

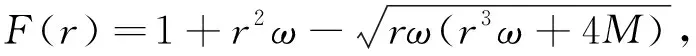
(2)

ω为HL参数，当r≫(M/ω)1/3时[19]，此解对应为广义相对论中的史瓦西黑洞.

HL黑洞时空中运动粒子的拉格朗日方程为

(3)

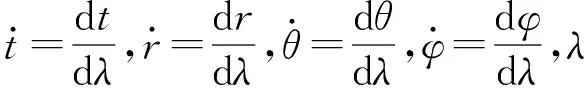
(4)

(5)

式(4)、(5)中的积分常数E和L分别是粒子的能量和角动量.

(6)

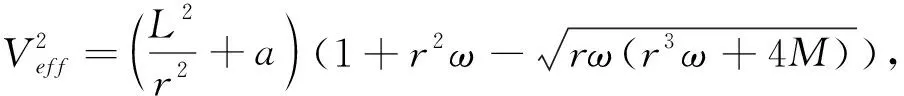
(7)

当a=1时，为类时测地线；当a=0时，为类光测地线.文中后面的讨论中取黑洞的质量M=1.

1.2 类时测地线结构

下面用有效势的方法研究HL时空中的类时测地线.首先利用控制变量法讨论粒子角动量L和参数ω对有效势的影响.由图1(a)可见，在ω=0.6的情形下，角动量L的逐渐增大引起粒子有效势势垒高度的增大.图1(b)描述了在角动量取L=4.15时，有效势势垒高度随着参数ω的增大而减小，同时当ω≫1时对应为传统的史瓦西黑洞时空中的情况.

(a) 不同角动量L (b) 不同参数ω图1 粒子有效势Fig.1 The effective potential of particle

接下来应用有效势的方法讨论类时测地线结构.取L=4.15，ω=0.6，画出粒子有效势图像如图2所示.由图2可知粒子运动轨道包括不稳定圆轨道、稳定圆轨道、束缚轨道、吸收轨道.

进一步利用方程(5)、(6)，做坐标变换，并对φ再次求导可得粒子运动方程：

(8)

(9)

下面将逐一分析图2所出现的各种轨道类型.

图2 类时测地线有效势Fig.2 The effective potential of time-like geodesic

1) 圆轨道.图2所表示的有效势曲线中的极值点对应粒子圆轨道的半径，满足条件：

(10)

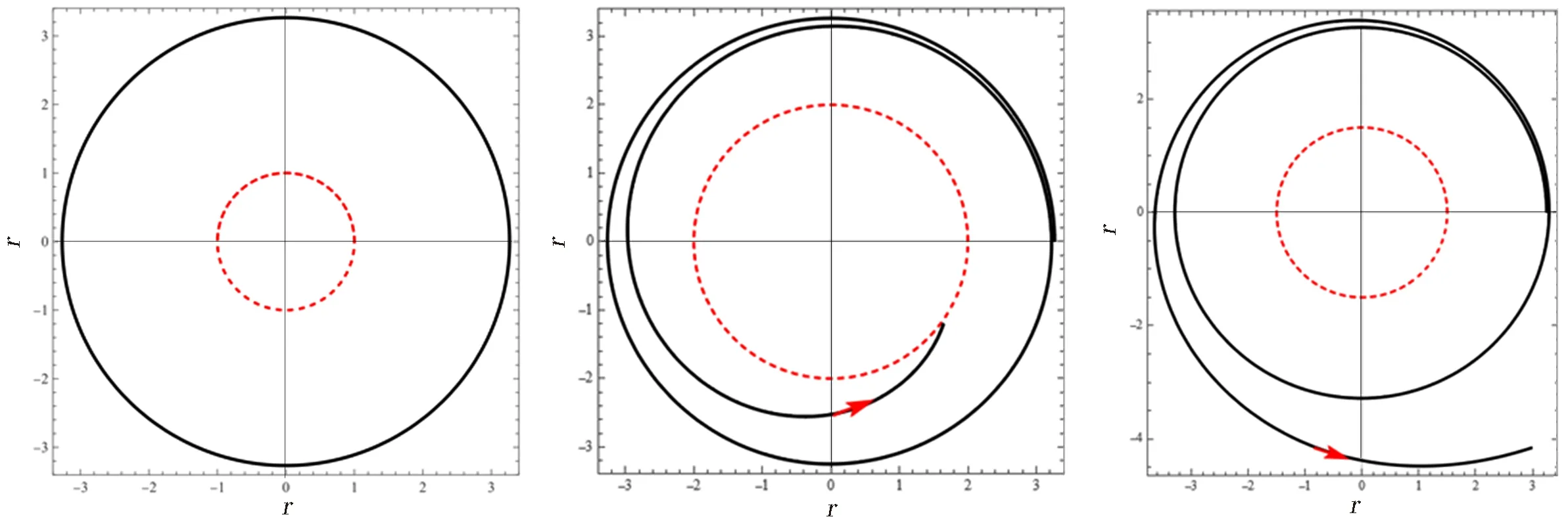
(a) 不稳定圆轨道 (b) 受扰动的不稳定圆轨道(c) 受扰动的不稳定圆轨道图3 类时测地线Fig.3 Time-like geodesic

图4 不稳定圆轨道半径随ω的变化图5 类时稳定圆轨道 Fig.4 Variation of the unstable circular orbit radius with ωFig.5 The stable circular orbit of time-like geodesic

图6表明在角动量L=4.15不变时，稳定圆轨道半径将随着ω的增大而减小，同时ω趋于无穷时，对应为史瓦西黑洞的稳定圆轨道半径 13.353M.

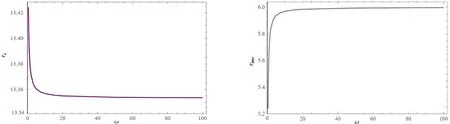
图6 稳定圆轨道半径随ω的变化 图7 最内层稳定圆轨道半径随ω的变化

2) 吸收轨道和束缚轨道.

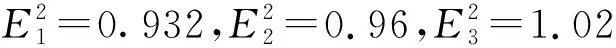
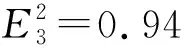
3) 最小半径束缚轨道.当粒子能量值E=1时，粒子有一个最小半径的束缚轨道rmb.图9研究了当角动量L=4.15时，参数ω对rmb的影响.由图9可知，最小半径束缚轨道rmb随着ω的增加而增大，直至接近史瓦西黑洞中的最小半径束缚轨道半径3.159M.

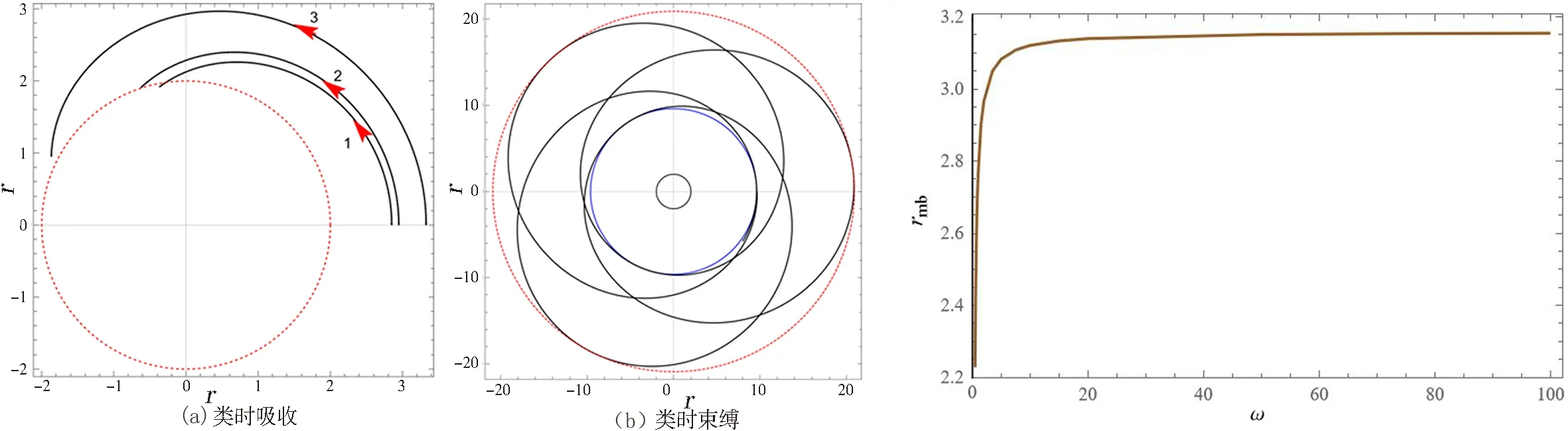
图8 类时吸收和类时束缚轨道 图9 最小半径束缚轨道随ω的变化Fig.8 The absorption and bound orbit of time-like geodesic Fig.9 Variation of the smallest radius of bound orbit with ω

1.3 类光测地线结构

下面将研究类光测地线结构.从图10可得到：当角动量L=4.15恒定时，类光测地线的有效势势垒高度随着参数ω的增大而减小(图10(a))；当固定参数ω=0.6时，可得有效势势垒高度随着角动量L的逐渐增大而增大(图10(b)).与类时测地线一样，当ω≫1时对应为传统的史瓦西黑洞时空中的情况.

接下来取L=4.15,ω=0.6，研究类光测地线的特征轨道(如图11).

(11)

由图11可知，与类时测地线不同的是：光子的轨道类型中没有稳定圆轨道和束缚轨道，只有不稳定圆轨道、吸收轨道和逃逸轨道.下面分析图11所出现的各种轨道类型.

(a) 不同参数ω (b) 不同角动量L图10 类光测地线的有效势图像Fig.10 Effective potential image of null geodesic

图11 类光测地线的特征轨道Fig.11 Characteristic orbit of null geodesic

(a) 不稳定圆轨道 (b) 受扰动的不稳定圆轨道 (c) 受扰动的不稳定圆轨道图12 不稳定圆轨道和受扰动的不稳定圆轨道的类时测地线Fig.12 The unstable circular orbit and disturbed unstable circular orbit of null geodesic

图13 光子不稳定圆轨道半径随ω的变化Fig.13 Variation of the unstable circular orbit radius with ω for null geodesic

取角动量L=4.15时，图13研究了参数ω对光子不稳定圆轨道半径的影响.结果表明：不稳定轨道半径随着ω的增大而增大，同时当ω趋于无穷时对应到史瓦西时空中的不稳定圆轨道半径3M.

2) HL黑洞阴影半径.黑洞阴影半径与不稳定圆轨道半径的关系为[20]

(12)

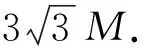
图14 黑洞阴影半径随ω的变化 图15 类光吸收轨道和类光逃逸轨道Fig.14 Variation of black hole shadow radius with ω Fig.15 The absorption and escape orbit of null geodesic

2 结语

利用有效势的方法仔细地研究了HL黑洞的测地线结构，特别讨论了HL引力参数ω对特征轨道的影响.研究结果表明：

1) 对于类时测地线，不稳定圆轨道半径ru、最内层稳定圆轨道半径rms以及最小半径束缚轨道rmb都比广义相对论中的相应半径小，且它们都随着HL黑洞时空中参数ω的增大而增大，当ω趋于无穷大时，回到史瓦西时空中对应半径3.869M、6M、3.159M；稳定圆轨道半径rs比广义相对论中稳定圆轨道半径大，且随着ω的增大而减小，当ω趋于无穷大时，回到史瓦西时空中对应半径值13.353M.