新型活塞式套筒阀在长距离重力输水系统中的应用

黄叶飘， 邱焕峰， 郑雪玉,2,3， 孙 卫

(1.中国电建集团 贵阳勘测设计研究院有限公司， 贵阳 550081；2.武汉大学 水利水电学院， 武汉 430072； 3.南京水利科学研究院， 南京 201129)

长距离重力输水系统中，阀门关闭是引起管道破坏的最主要原因。阀门突然关闭会引起管道中该处压力急剧升高，并且以很快的速度沿管道传播。管道中的压力传到水库变为负压反向继续传播，在管道的转弯点或者高点出现压力最小值，当压力小于水的气化压力时产生液柱分离，分离的水柱再弥合时的压力是设计压力的几十倍，导致管道的破坏[1-2]。因此，防止关阀时管道中产生液柱分离是保护管道系统安全运行的重要条件。

本文结合工程实例，将一种新型阀门应用于工程中，在此需要已知阀门的基本流量特性。目前可以通过实验和数值模拟的方法研究阀门特性。数值模拟方法节约成本及时间，操作方便。姜健等[3]、李颖等[4]、冯卫民等[5-6]已通过数值模拟的方法计算阀门内部三维流场，研究表明数值模拟的结果是可靠的。文中通过CFD方法，对多功能活塞式套筒调节阀建模并进行数值计算，得到阀门无量纲开度曲线。计算水锤压力的方法包括有限差分法、有限单元法、特征线法等，特征线法在计算管道瞬变流时方法简便，适宜于电算。刘志勇等[7]、张志军等[8-9]、宋乃硕等[10]根据特征线法，模拟计算长距离重力流管道的水锤及其防护。本文采用特征线法，编写代码计算管道关阀过程中的水锤压力。通过计算，寻求合适的关阀策略，防止因关阀而产生压力破坏，保障系统安全运行。

1 阀门数值模拟

DN1200多功能调节阀是一种活塞式套筒阀，结构如图1所示，公称直径为1 200 mm，主要由阀体、活塞缸、阀杆、连接杆、套筒、导向块等元件构成。流体自阀体与活塞缸之间的通道流入，经过套筒上的开孔流向下游。当控制机构转动阀杆时，连接杆带动套筒在导向块的约束下左右移动，改变过流面积来实现调流调压等目的。该型调节阀的套筒上为圆孔形开口，沿套筒环向均匀分布，水流流出网孔时会形成高速水流，并沿径向向管径中心喷射，相互撞击实现消能。

图1 新型活塞式套筒阀结构

对套筒阀建模划分网格，并进行CFD数值计算，根据计算结果绘制出该阀的无量纲流量特性曲线，如图2所示，图2中横坐标表示阀门的相对开度α，纵坐标是阀门对应开度下流量系数与最大流量系数之比τ。从图2可知，调节阀的流量特性为对数型，流量变化速度逐渐加快，小开度时流量变化缓慢，调节精度高，大开度时流量变化相对较快，能保持良好的调节能力。

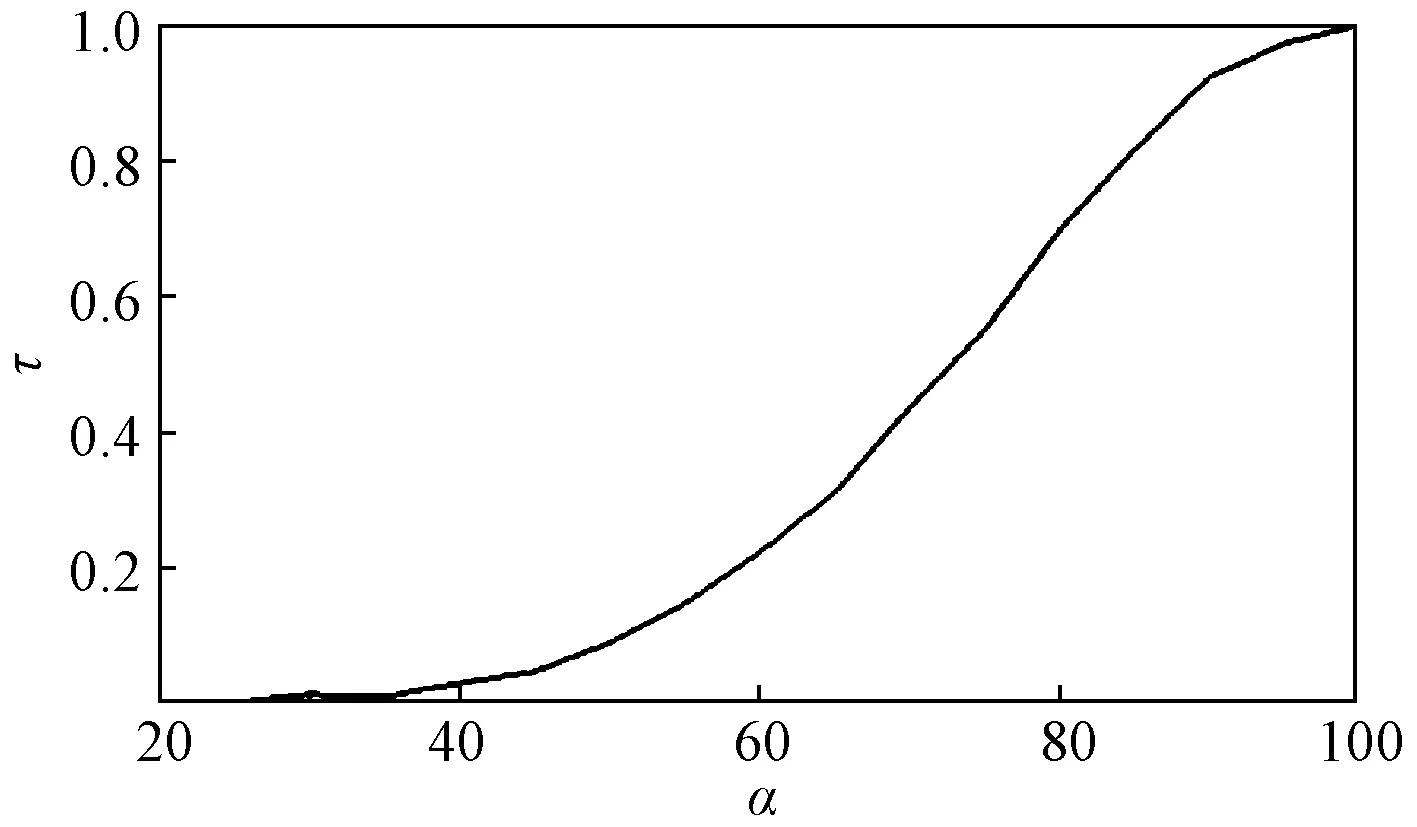
图2 阀门的无量纲特性曲线

2 水锤压力计算

水锤基本方程的理论基础是水流运动的力学规律和连续原理，包括运动方程和连续方程，两者皆为偏微分方程[1]，即

(1)

(2)

式中：V、H分别为产生水锤时管中流速和测压管水头；f、D、g分别为管道摩阻系数、管径、重力加速度；a、x、t分别为水锤波传播速度、距离、时间。

将以上水锤偏微分方程通过特征线转化为全微分方程后进行积分，得到能进行数值计算的有限差分方程。在特征平面x-t平面上，将管道分成n段，每段长度为Δx，选取合适的时间步长Δt，对于特征网格上任意一点P，H、V为

HPi=Hi-1-B(QPi-Qi-1)-RQi-1|Qi-1|

(3)

HPi=Hi+1+B(QPi-Qi+1)+RQi+1|Qi+1|

(4)

式中：Q为流量；B为管道的特征常数，计算公式为

(5)

R为管道的摩阻特性常数，计算公式为

(6)

式中，A为管道界面面积。

管材为球墨铸铁管，水锤波在管中传播速度为

(7)

式中：K为流体的体积弹性模量，水取2.06×109Pa；D为管道直径，取1.4 m；E为管壁材料的弹性模量，球墨铸铁管取1.60×1011Pa；δ为管壁厚，取17.1 mm。

基于以上基本方程，考虑进水池、中部检修阀及末端阀门等边界条件，计算云南某工程长距离自流引水系统，管道总长10 360 m，进水池水位1 520.484 m，出水池水位1 501.061 m，管材采用球墨铸铁管，管道半径1.40 m，在桩号G4+797处设支管，在分叉处设有检修阀门，支管半径为0.40 m，长1 482.00 m，支管末端设有控制阀。

在整个关阀过程中，水柱分离发生在管道凸起部位，关阀也会在阀门处产生高压，因此计算工况及计算内容为：①主管末端阀门关阀后系统中的压力变化及末端阀门处压力瞬时值；②中部检修阀门关阀后系统中的压力变化及末端阀门处压力瞬时值；③主管末端和支管末端阀门组合关闭后主管中压力变化及末端阀门处压力瞬时值。

3 计算结果分析

3.1 稳态计算结果

首先计算稳态运行时的结果，考虑管道的沿程水头损失及局部水头损失，计算得到稳态时主管流量为2.6 m3/s，支管流量为0.3 m3/s。将稳态计算得到的流量和压力水头作为初值进行非恒定流的计算。

3.2 主管末端阀门关闭计算结果

经计算，主管末端阀门关闭使管道不产生液柱分离的最小关阀时间为65 s，考虑到阀门关闭后尽快起到节流效果，且不能产生过大的水锤压力，故采取两阶段关阀方案，即前5 s关闭60%，后60 s慢关。当总计算时长为150 s时，所得到末端阀门节点的压力随时间变化和沿程压力包络线如图3和图4所示。

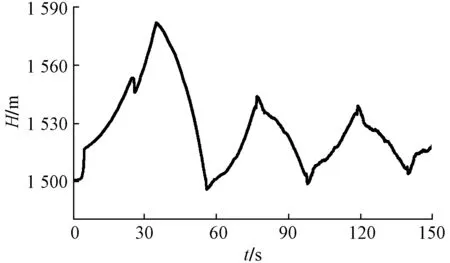
图3 主管末端阀门处压力瞬变特性

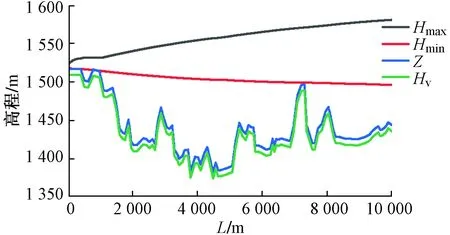
图4 主管末端阀门关闭压力包络线

根据计算结果，前5 s快速关阀，产生一个压力峰值向上游传播到达上游水池，压力恢复为稳态值，向下游传播，一个相位后到达末端阀门处，此时阀门末端承受压力应变为负压。由于此时阀门尚未完全关闭，压力仍在升高，上一阶段阀门快关产生的压力波只引起一个压力向下波动，压力继续上升到达压力最大点。之后阀门节点的压力周期性变化，由于管道摩阻引起能量损失，压力峰值逐渐减小。

从图4看出，全程L最小压力皆大于水的气化压力线，因此不会发生水柱分离。整个管道容易发生液柱分离的点为靠近出水池段以及山体凸出管段。这些管段的高程高，稳态时测压管水头很小，压力同等降低的情况下较其他管段更容易发生液柱分离并被破坏。高程低的管段在压力同等升高情况受到的压力水头更大，超过管道强度也会发生破坏。关阀后的压力包络线显示全程不会发生液柱分离破坏，阀门承受的最大压力为1.67 MPa，最大压力变化值为0.79 MPa，在阀门允许承压范围内，因此管道运行安全。

3.3 主管末端阀门及支管末端阀门组合关闭计算结果

经计算，主管末端阀门和支管末端阀门组合关闭工况时，支管末端阀门10 s匀速关闭，主管末端阀门前5 s关闭60%，后70 s慢关，才能使主管中不发生水柱分离破坏，计算得到沿程压力包络线和末端阀门节点的压力随时间变化如图5、图6所示。支管末端阀门关闭后，压力向主管方向传播，到岔管处，压力波向主管上下游传播，与主管末端阀门引起的压力叠加。从压力包络线中看出易出现水柱分离和管道承受压力最大的管段和末端阀门关闭工况下相同，阀门处的压力变化规律也相近，由于支管的影响，压力线有小的波动，包络线不如主管末端阀门单独关闭时光滑。关阀使阀门承受的最大压力为1.79 MPa，在阀门末端，压力变化值最大为0.83 MPa。支管末端阀门关闭后使得主管承受的最大压力增加0.12 MPa，同时末端阀门的允许关阀时间延长。

图5 主管和支管末端阀门关闭压力包络线

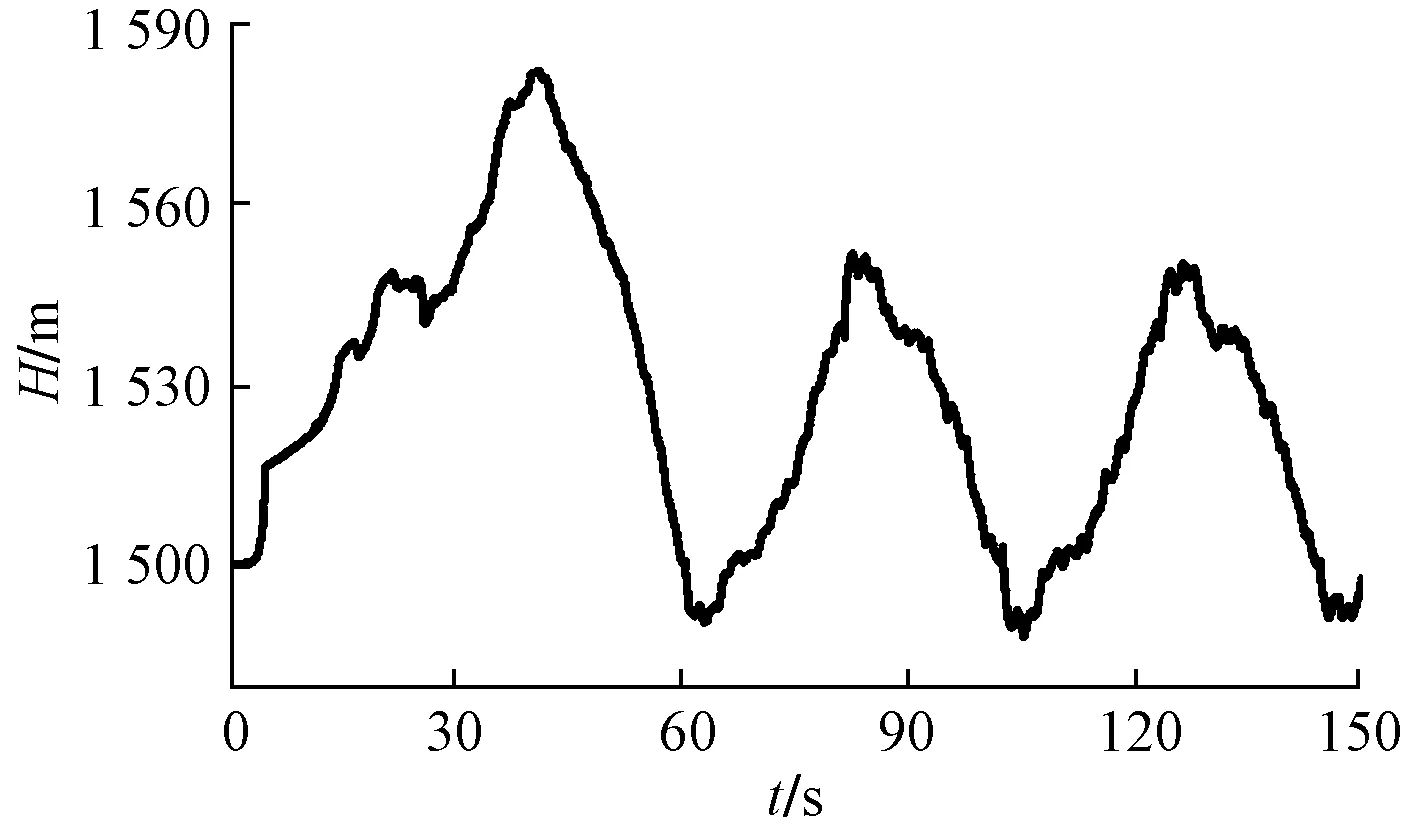
图6 主管和支管末端阀门关闭主管末端阀门处压力瞬变特性

3.4 中部检修阀门关闭计算结果

经计算，中部检修阀门关闭工况时，阀门关阀规律采用前5 s快关60°，后120 s慢关，才能使主管中不发生水柱分离破坏。与前两种工况不同，中部检修阀门关闭阀下游压力急剧下降，较上游更容易发生水柱分离现象。从图7可知，下游的最大压力包络线几乎与稳态时的测压管水头先重合，因此允许下游压力降低的幅度很小，这也是下游容易发生真空的原因。阀前压力变化如图8所示，关阀过程中阀门前后压力相互影响，前80 s内阀前压力持续上升，期间由于下游波影响存在向下的突变，之后周期性地波动变化。管道承受的最大压力为1.50 MPa，在桩号G4+797检修阀门处，压力变化值最大，最大为0.24 MPa。由于阀门关闭缓慢，上游最大压力并不大，因此管道运行安全。

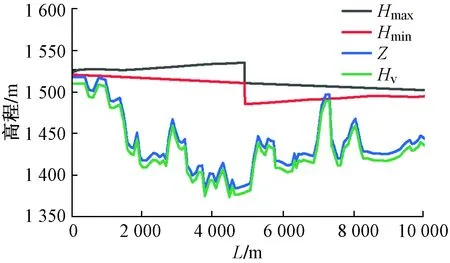
图7 中部检修阀门关闭压力包络线

图8 主管和支管末端阀门关闭主管末端阀门处压力瞬变特性

4 结论

1)通过CFD数值模拟计算，新型活塞式套筒阀的流量特性为对数型。

2)通过编写程序建立管道和阀门的数学模型，计算得到各工况下使得管道不发生水柱分离的套筒阀关闭时间。结果表明新型阀门采用两阶段关闭时，快关能够快速截流，慢关具有良好的调节精度，因此新型套筒阀应用于工程中能很好地保障工程正常运行。

3)通过计算管道末端阀门合理的关阀时间控制管道系统中不发生水柱分离，对管道运行过程中阀门关闭程序具有指导意义。

4)在不采取调压塔、空气阀等水锤消除措施时，应严格关阀时间控制。本文关阀规律只适用文中提到的阀型及供水系统，不同的阀门及管道布置系统具有不同的特性，应具体问题具体分析。