抗舷外有源诱饵方法研究

刘业民 李永祯 邢世其 王明珠 黄大通

（1. 国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室，长沙 410073；2. 中国人民解放军第32579部队，桂林 541001）

引 言

舷外有源诱饵通过接收、放大和转发雷达导引头信号形成假目标，与水面舰艇的真实回波信号共同作用来完成对反舰雷达导引头的角度诱骗，其干扰机理与箔条质心干扰的作用原理相同[1]. 当存在舷外有源诱饵干扰时，若继续根据单脉冲测角系统的角误差信息进行跟踪，雷达导引头将会错误地跟踪假目标，最终导致整个攻击过程的失败. 因此，如何有效地对抗舷外有源诱饵干扰，是提高反舰导弹作战效能的根本所在，具有非常重要的军事意义.

在海战中，对于反舰雷达导引头而言，舷外有源诱饵是一种非常有威胁的干扰方式[1]. 目前，关于舷外有源诱饵方面的研究主要从干扰的角度进行，如诱饵布放研究、诱饵弹定高飞行控制技术、诱饵作战使用、仿真模型验证以及干扰效果评估等等[2-8]. 而从抗舷外有源诱饵干扰角度的研究相对较少，且主要集中在以下两个方面：一是舷外有源诱饵干扰的检测问题，它是抗舷外有源干扰的前提和基础. 杜晓宁等[9]研究了基于广义似然比检验(generalized likelihood ratio test, GLRT)有源诱饵干扰的存在性检测；来庆福[1]进一步考虑了基于惯导信息辅助和基于GLRT有源诱饵存在性的双门限检测方法，该方法可进一步提高检测概率. 二是抗舷外有源诱饵干扰方法的研究. 由于惯导信息不受射频干扰的影响，付海波[10]和来庆福[1]分别研究了利用惯导信息抗舷外有源诱饵干扰方法，当雷达导引头检测到质心干扰时，导弹改用惯导信息制导，以避免舷外有源诱饵干扰引偏导弹. 然而，惯导制导的累计误差可能会影响其跟踪精度. 张树森等[11]提出了末制导雷达发射复杂信号对抗舷外有源雷达诱饵的方法，末制导雷达发射机发射3种脉冲信号，分别为诱导脉冲、制导脉冲和遮盖脉冲，使敌方电子对抗侦察机难以识别和分辨制导信号，但该方法增加了系统研发的成本和复杂度. 文献[12]提出了一种抗箔条质心干扰的新方法，该方法的核心思想是把抗箔条质心干扰的本质看作是两个不可分辨目标的角度估计问题，根据舰船目标和箔条干扰的统计特性，通过估计出目标的到达角(angle of arrival, AOA)以此来达到抗箔条质心干扰的目的. 对于舷外有源诱饵干扰的情况，舰船按照战术使用原则在雷达照射波束内布放舷外有源诱饵，通过诱饵生成的假目标与舰艇真实回波信号共同作用形成质心干扰. 此时，舰船目标与假目标均在雷达导引头的照射波束内无法分辨，可视为两个不可分辨的目标. 因此，可以借鉴文献[12]的抗箔条干扰思路，研究如何对抗舷外有源诱饵干扰的方法.

基于上述背景和问题，本文以单脉冲测角系统为对象，研究了舷外有源诱饵干扰条件下目标AOA的估计问题，提出了两种可选的目标AOA估计方法：改进的最大似然(improved maximum likelihood,IML)角度估计方法和矩估计(moment estimation,MM)角度估计方法. 在理论分析的基础上，通过蒙特卡洛仿真实验对本文所提方法进行了仿真实验验证，并与其他文献所提方法和克拉美罗下界(Cramér-Rao lower bound, CRLB)进行了估计性能对比.

1 信号模型

在典型的比幅单脉冲雷达系统中，雷达利用四个子波束来估计目标的角度信息. 处于同一水平(垂直)面的两个子波束为方位(俯仰)角波束，其形状相同，且与天线视轴左右(上下)对称排列，以一定的角度重叠. 处于同一水平面的两个子波束用于估计目标的方位角，而处于同一垂直面的两个子波束用于估计目标的俯仰角[13]. 在舷外有源质心干扰情形下，角度欺骗主要是在方位角上，因此，本文主要讨论目标方位角的估计问题.

当舷外有源诱饵干扰存在时，在相同的距离和角度单元里面同时包含了舰船目标和假目标信号，如图1所示，单脉冲测角系统和、差通道中所接收到的回波信号可表示为：

图1 舷外有源诱饵形成质心干扰示意图Fig. 1 Diagram of centroid jamming formed by off-board active decoy

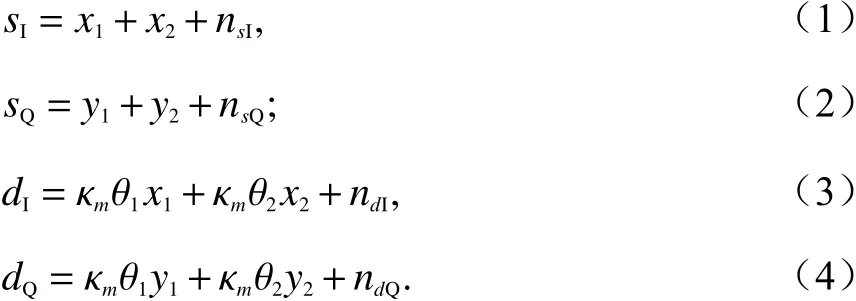
式中：s表示和信号；d表示差信号；n表示和、差通道雷达接收机中的热噪声和杂波信号；下标 I 和 Q分别表示信号的同相和正交分量；随机变量x1和y1分别表示 I 通 道和 Q通 道中目标回波；随机变量x2和y2分别表示 I 通道和 Q通 道中假目标干扰回波； θj(j=1,2)表示目标(或干扰)的AOA； κm为单脉冲斜率，在天线设计阶段，该参数先验可知.

根据文献[14]，若单脉冲系统中的杂波信号可通过信号处理的方法得到很好的抑制，则可以合理地假设雷达接收机中热噪声服从零均值的高斯白噪声，且和、差通道中同相和正交分量的高斯白噪声彼此相互独立，它们的方差分别为：

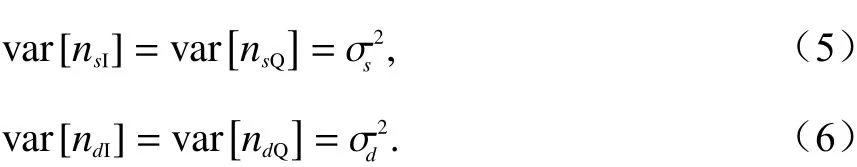
式中， var[·]表示求方差操作符. 目前的单脉冲测角系统在大多数情况下都能较好地估计出热噪声的方差[15]，因此，在本文中假设各路通道中热噪声的方差是已知的.

2 目标和舷外有源诱饵干扰回波的统计特性

在第1节的基础上，本节进一步分析舰船目标和舷外有源诱饵假目标干扰回波的概率分布特性.为此，将舰船目标回波和假目标干扰回波表示为

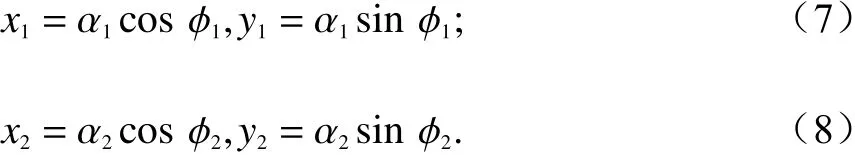
式中： α1和 α2分别表示舰船目标和假目标干扰回波的幅度； φ1和 φ2分别表示舰船目标和假目标干扰回波的相位.

在反舰应用中，假设舰船目标的雷达散射截面积(radar cross section, RCS)服从Swerling IV模型[16]，考虑其相位在[0, 2π]服从均匀分布[17]，不难得到目标回波x1的概率密度函数(probability density function,PDF)为

舷外有源诱饵的干扰机理是通过对接收到的雷达导引头信号进行放大转发，模拟出目标的回波信号，同时要求对反舰导弹雷达导引头形成质心干扰效应，使得诱饵发射的干扰回波所产生的假目标与舰船目标处于同一距离和方位分辨单元内，以此来实现对来袭反舰导弹的角度诱骗[1]. 据报道，美国的Nulka有源诱饵、AN/SSQ-95(V)系列有源诱饵以及英国的TOAD舷外有源诱饵系统等均具备模拟目标回波特性的能力[18]. 因此，这里可以合理地假设舷外有源诱饵干扰回波与舰船目标回波信号具有相同的统计特性[1]，即随机变量x2的PDF可表示为

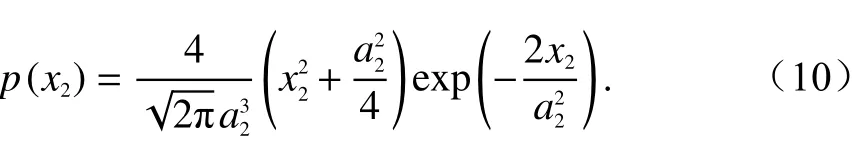
3 估计目标角度方法

利用第2节舰船目标和舷外有源诱饵干扰回波的统计特性，舰船目标和舷外有源诱饵干扰的AOA可通过最大化下面似然函数求得，即

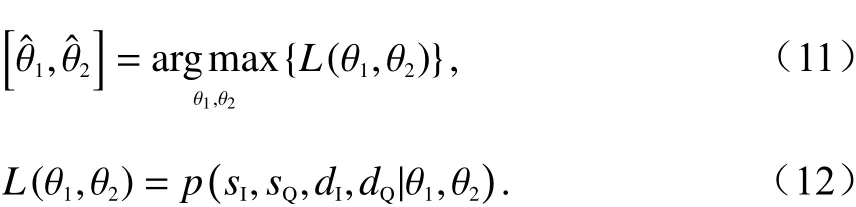
文献[17]基于式(12)推导了似然函数L(θ1,θ2)的表达式，并提出了最大似然(maximum likelihood,ML)角度估计方法. 然而，该方法有两点不足：一是数学推导过程过于复杂繁琐；二是实现该方法的计算量较大，可能会因实时性要求限制其应用. 为此，针对文献[17]所提方法的不足，本文在舷外有源诱饵形成质心干扰的条件下，提出了两种新的角度估计方法：IML角度估计方法和MM角度估计方法，下面分别详细阐述这两种角度估计方法.

3.1 IML角度估计方法

考虑到同相和正交通道中回波信号彼此间相互独立[15]，式(12)可以写成

将式(1)～(6)、(9)～(10)代入式(13)中，借鉴文献[17]的推导思路，可求得式(13)中似然函数的子函数LI(θ1,θ2)为

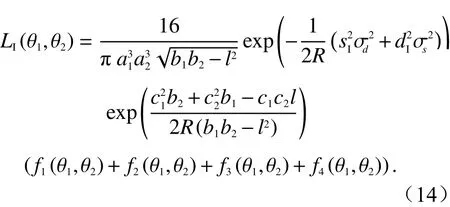
式中：

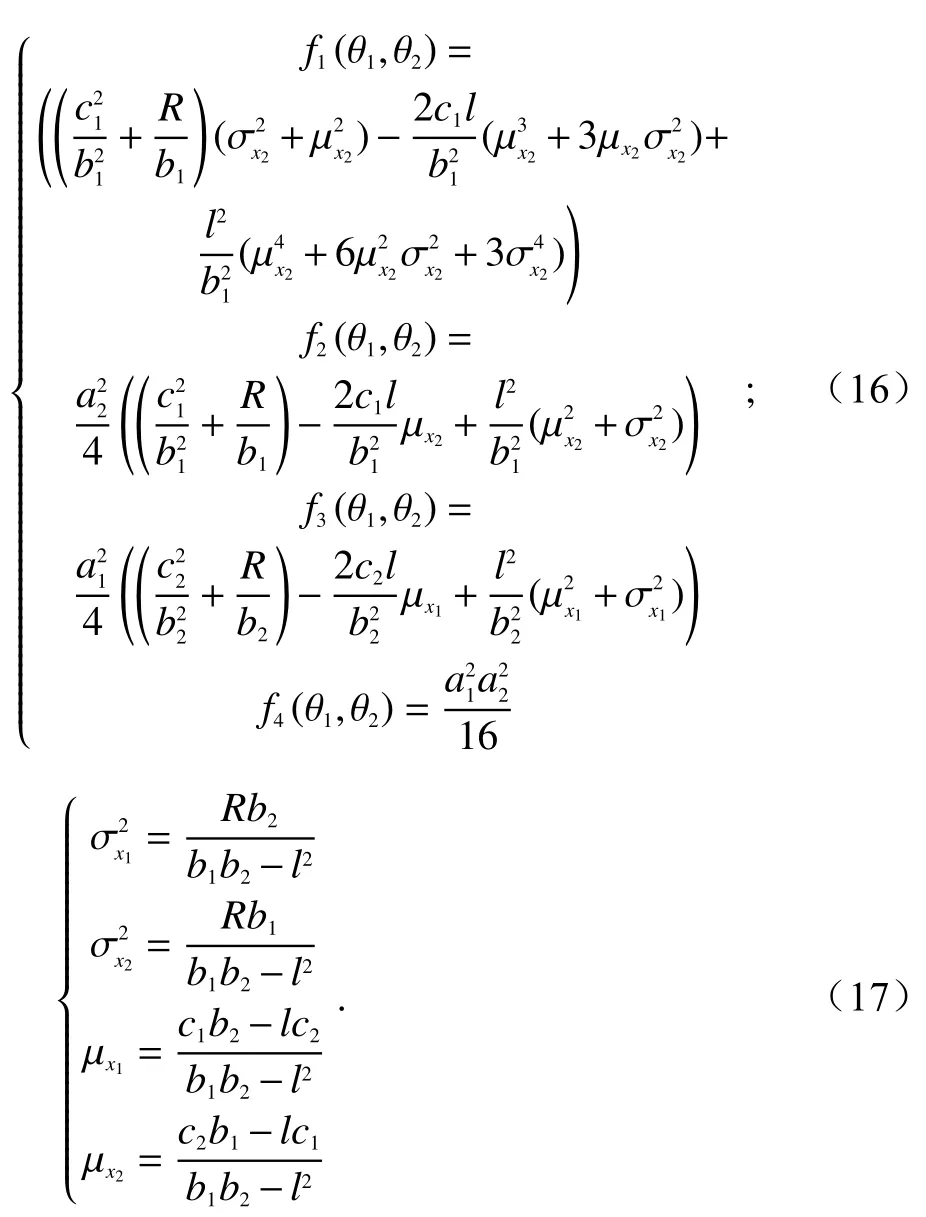
同理，按上述方法可求得似然函数的子函数LQ(θ1,θ2)，其表达式只需要把式(14)和式(15)中的sI和dI置 换 成sQ和dQ即 可. 将LI(θ1,θ2)和LQ(θ1,θ2)代 入式(13)，最终可得到似然函数L(θ1,θ2).

似然函数L(θ1,θ2)的闭合解通常无法求得. 一种可行的办法就是采用网格搜索法来获得目标和假目标干扰的AOA[17]，为此，图2给出了对数似然函数lg(L(θ1,θ2))的高程图. 其中目标的信噪比(signal-tonoise ratio，SNR)为25 dB，信干比(signal-to-interference ratio, SIR)为−4 dB，子脉冲数N为12. 目标和假目标干扰的真实AOA值分别为0.187 5 rad和−0.125 rad.从图2容易看出，目标和假目标干扰的AOA均有两个最大值，其中一个为虚假估计量，另一个为准确估计量，其目标和假目标干扰AOA的准确估计量分别为0.194 9 rad和−0.110 2 rad. 为得到准确的估计值，需要知道 θ1和 θ2的相对大小，这一先验信息可以从文献[16]所提方法中获取.

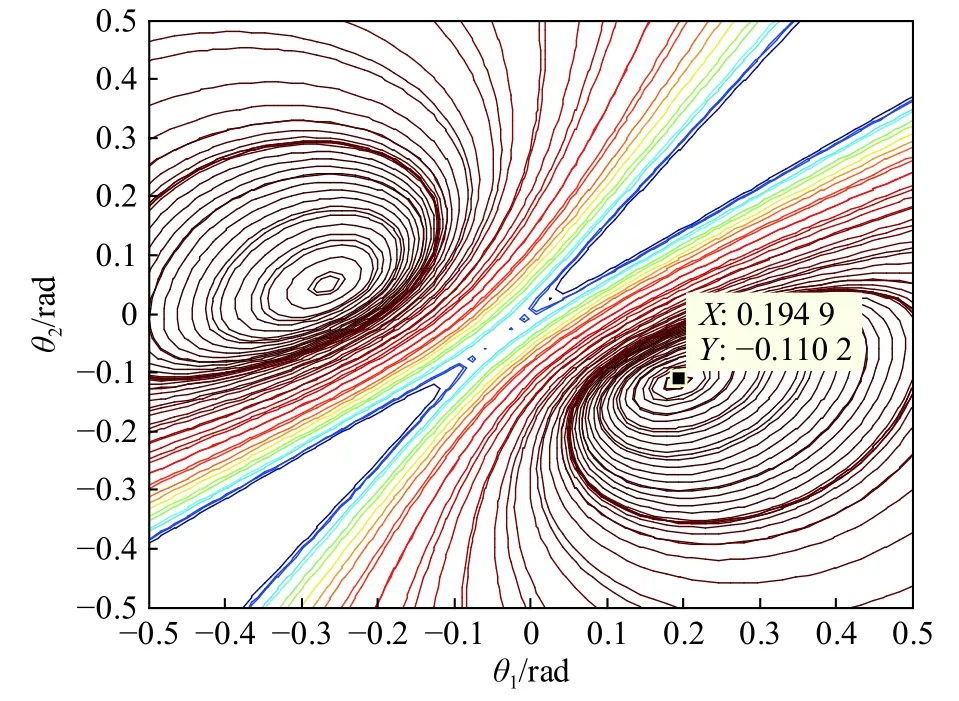
图2 对数似然函数lg(L(θ 1,θ2))的高程图Fig. 2 Contour plot of the log-likelihood function lg(L(θ 1,θ2))

此外，与文献[15]和文献[17]类似，这里假设舷外有源诱饵干扰和舰船目标的相对雷达横截面积(relative radar cross section, RRCS)是已知的，则可从和通道回波信号中估计出和，且有

3.2 估计量的CRLB和渐近性及算法复杂度分析

首先分析AOA估计量的CRLB. 对于两个不可分辨的Swerling IV目标，由于式(13)的似然函数是sI、dI、sQ和dQ的无限多项式，因而CRLB的闭合解通常无法得到. 不过，可以利用大数定律求得数值的CRLB[17]. 为此，对式(13)取对数，AOA估计量的Fisher信息可由下式计算得到：

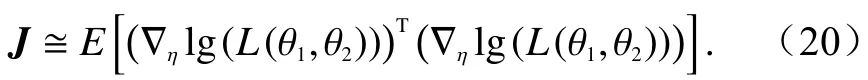
式中：≅表示等价于操作符；∇表示求梯度操作符.

利用大数定律，有

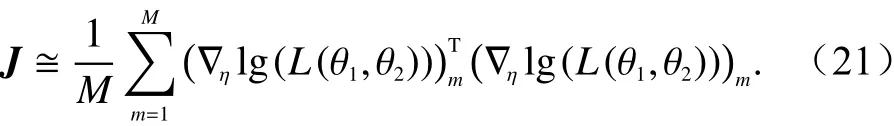
式中，下标m表示和通道与差通道的样本回波数据(即sI、dI、sQ和dQ) 的序号，当样本数M足够大时，可以很好地得到AOA估计量的CRLB数值解.

此外，若采用频率分集技术[19](即sI、dI、sQ和dQ彼此相互独立)，则利用N组子脉冲数， θ1和 θ2估计量的Fisher信息可由下式计算得到：

对式(22)中的矩阵J求逆，得到逆矩阵J−1，最后N可以求出 θ1和 θ2估计量的CRLB.

接着分析AOA估计量的渐近特性. 文献[20]研究表明，若目标和干扰的SIR为−7～7 dB，则式(1)～(4)的PDF可近似为高斯分布. 由于在舷外有源干扰情形下，该条件通常是满足的，因此，式(12)中的似然函数L(θ1,θ2)可近似为二维联合高斯分布. 则随着N的增大，AOA估计量和具有渐近分布特性，即[21]

式 中： N(·)表示高斯分布；I−1(θ1)和I−1(θ2)分 别 为JN−1(1,1)和JN−1(2,2).

图3 估计量的渐近分布特性Fig. 3 Asymptotic distribution of estimate

表1给出了N= 4、8、12、16时，和I−1(θ1)的数值计算结果，容易看出，随着样本数的增加(即N的增加)，越接近真值越接近I−1(θ1)， 即估计量渐近服从于式(23)给出的高斯分布特性.

表1 估计量随不同子脉冲数变化的渐近分布特性Tab. 1 Asymptotic distribution of estimate with different subpulses rad

表1 估计量随不同子脉冲数变化的渐近分布特性Tab. 1 Asymptotic distribution of estimate with different subpulses rad

N E[ˆθ1] θ1 var[ˆθ1]I−1(θ1)4 0.110 3 0.125 0.004 0 0.003 6 8 0.118 2 0.125 0.001 8 0.001 7 12 0.120 4 0.125 0.001 3 0.001 1 16 0.121 7 0.125 0.000 8 0.000 8

最后分析一下IML方法的计算复杂度. 为便于分析，假设两个数的加、减、乘和除，以及数的开方和取对数运算均视为1次浮点运算. 若AOA θ1和 θ2在其各自取值范围内均划分成M等份，子脉冲数为N，则式(18)和式(19)的计算量为4N+11次、式(13)的计算量为 1 16M2N+20M2+41N+19次、网格搜索法的最大计算量为M(M−1)次，最终可得IML方法的总计算量为1 16M2N+21M2−M+ 45N+ 30次，其计算复杂度为O(116M2N). 类似上面的分析和计算，同样可得到文献[17]所提方法的总计算量为153M2N+21M2−M+12N+30次 ，其计算复杂度为O(153M2N).由此，可算出本文所提方法的计算效率比文献[17]所提方法的计算效率提高了约25%.

下面定量分析一下算法的实时性和可行性. 取M=60，N=12，则IML方法的总计算量约为5.0×106次，而当前CPU处理器的计算速度一般可达到每秒2×109次的浮点运算能力. 由此可推算出利用IML方法估计1次目标AOA的时间约为0.002 5 s. 在反舰应用中，驱逐舰的航速一般约为30 n mile/h[1]，即15.4 m/s，则在使用本文所提的IML方法估计1次角度的时间内，舰船航行了约0.039 m. 在该时间内，即使舰船相对于导引头做横向规避动作，相对于雷达导引头而言，舰船的角度值改变约为 3.9×10−6rad(假设弹目之间距离为104m)，这一角度变化值比角度估计误差还要小，因此可以忽略不计. 通过上面分析可知，从算法实时性的角度来看，本文所提IML方法的算法复杂度在工程实现上是可行的.

3.3 MM角度估计方法

由3.1节可知，通过假设回波信号的同相和正交分量相互独立，在文献[17]的基础上提出了一种IML角度估计方法，与文献[17]所提方法相比，IML方法在保证估计精度高的同时，可进一步简化似然函数数学推导的复杂性和表达式的简洁性. 但该方法的闭合解通常无法求得，仍需通过搜索来估计出目标的AOA. 为此，本节提出了一种MM角度估计方法，该方法在估计精度和实时性之间进行了折中，且在高SNR和脉冲积累数多的情况下，与IML方法的估计性能相当. 下面详细阐述该估计方法的基本思路.

基于第2节中回波信号统计特性模型，可以合理地假设舰船目标回波x1、舷外有源诱饵假目标干扰回波x2以 及杂波和噪声nsI彼此间相互独立. 为此，根据式(1)、(5)、(9)～(10)，可求得和通道同相分量sI的二阶矩为

同理，根据式(3)、(6)、(9)～(10)，可求得差通道同相分量dI的二阶矩为

由前面分析可知：和通道中正交分量sQ与同相分量sI的 PDF相同；差通道中正交分量dQ和同相分量dI的PDF相同. 因而，和通道与差通道中正交分量的二阶矩与同相分量的二阶矩是相同的.

类似地，同样可以得到和、差通道同相分量的二阶矩，即

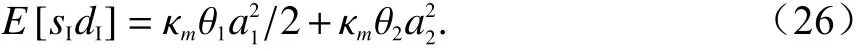
另一方面，式(24)～(26)中的二阶矩可通过N个独立子脉冲的回波信号估计出来，即

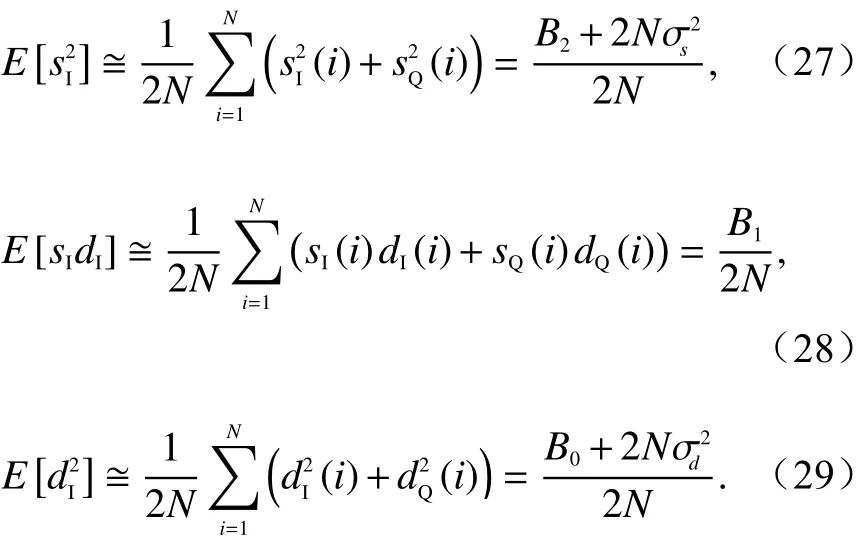
式中：

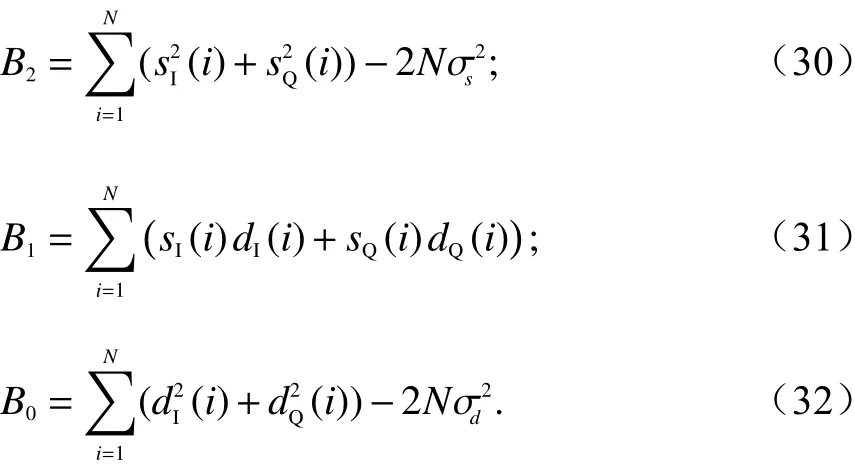
然后，根据式(24)～(29)，结合式(19)，联立成方程组，可求得舰船目标的AOA为

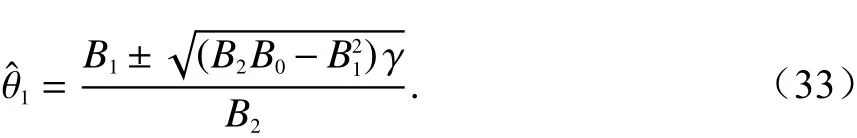
式(33)有两个解，确定唯一解由 θ1和 θ2的相对大小来决定. 不失一般性，若 θ1>θ2，则求得舰船目标估计的AOA为

下面分析MM方法的算法复杂度. 类似于前面的分析，式(30)～(32)的计算量为12N+5次，式(34)的计算量为7次，则MM方法的总计算量为12N+12次，其计算复杂度为O(12N). 可见MM方法比IML方法和文献[17]所提方法的算法复杂度要小约M2倍数量级.

4 仿真实验

本节中，首先比较IML方法和MM方法的AOA估计性能. 为简便起见，这里忽略天线增益问题，每组仿真结果进行5 000次蒙特卡洛仿真实验. 不失一般性，假设和、差通道中噪声和杂波信号的方差均为1，即 σs2=σd2=1. 对于一个典型的单脉冲测角系统，单脉冲斜率与和通道中雷达天线半波束宽度一般满足关系式 κm≈2θBW. 取 κm=1.6， 则有 θBW=0.5 rad.为了遍历目标与舷外有源诱饵生成的假目标的相对可能位置，仿真中目标的位置相对于天线视轴方向逐步变化. 即固定 θ1−θ2=0.25 rad，根据质心干扰的特点，由于天线视轴方向位于舰船目标与假目标夹角之间，因此，仿真中舰船目标的角度开始时位于天线视轴方向上(θ1=0 rad)，结束时假目标的角度位于天线视轴方向上(θ1=0 .25 rad)，θ1的步进率为0.023 7 rad，两者的相对位置关系如图4所示.

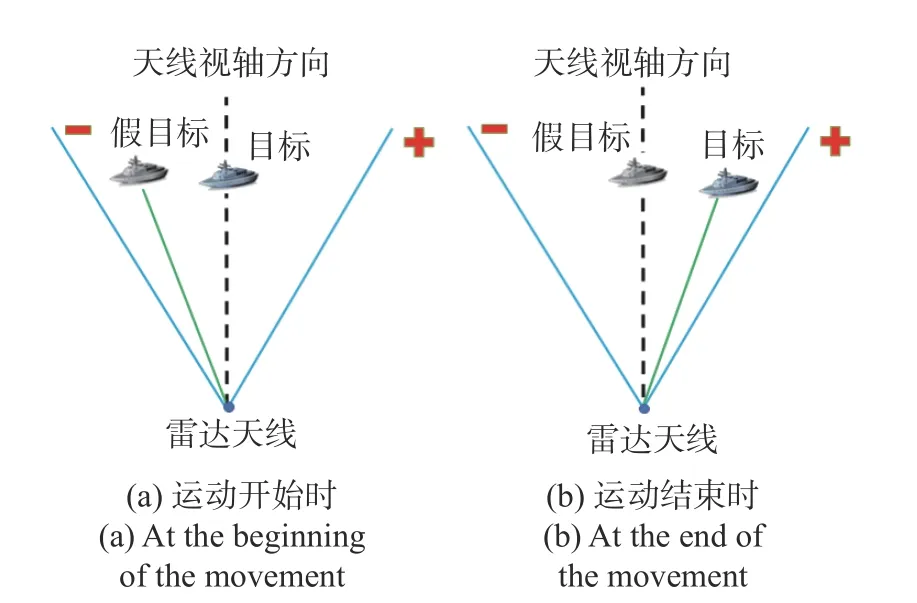
图4 舰船目标和假目标相对位置关系示意图Fig. 4 Schematic of the relative position of vessel target and decoy

下面通过计算目标AOA的均方根误差(root mean square error, RMSE)来定量分析不同的子脉冲数N、SNR和SIR对估计目标AOA的性能影响. 在IML方法中，搜索步进率均为0.006 2 rad. 图5给出了不同子脉冲数对目标AOA估计性能影响的仿真结果. 对于每一组子脉冲数N，固定SNR和SIR，即：SNR=20 dB, SIR=−4 dB. 从图5可以看出，在 θ1变动的区间内，两种方法均保证了稳定的估计性能，且随着子脉冲数的增加，目标AOA估计也得到了有效的改善(即RMSE变得更小). 同时也可以看出，在相同的子脉冲数情况下，IML比MM方法的估计性能稍好.特别地，随着子脉冲数的增加，MM方法越来越接近IML方法的估计性能. 在图6中，为了验证本文所提方法的估计性能，将IML方法与CRLB的平方根进行了对比，容易看出，单脉冲系统通过积累子脉冲数可有效改善目标AOA的估计性能.

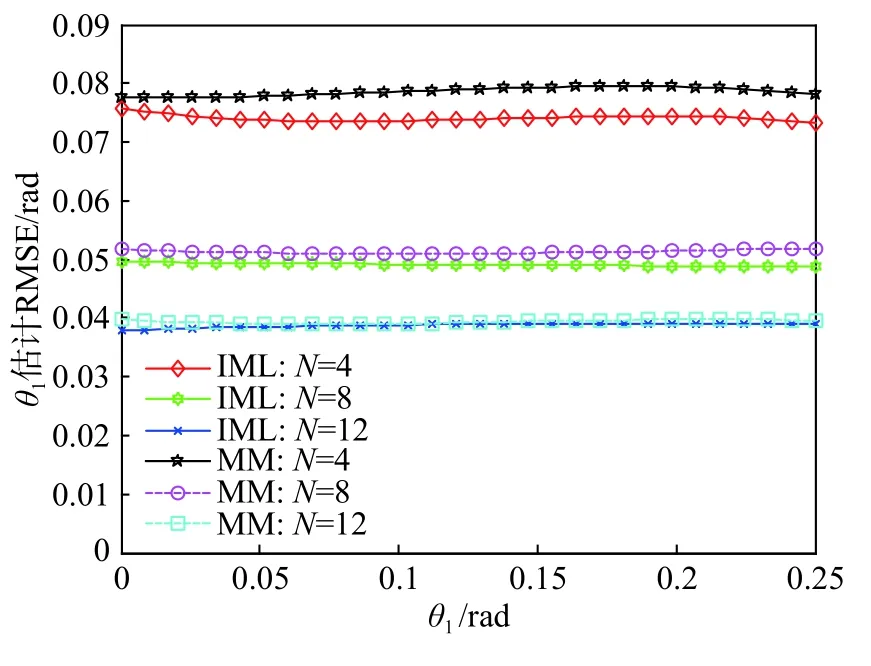
图5 不同子脉冲数对目标AOA估计性能的影响Fig. 5 Effect of performance of the target AOA for various values of subpulses

图6 IML估计性能与CRLB平方根的比较Fig. 6 Comparison of the square root between the IML method and CRLB

接着分析SNR和SIR对目标AOA估计性能的影响. 图7(a)给出了目标AOA的RMSE与CRLB平方根随SNR变化的曲线关系. 设定仿真参数为：SIR=−4 dB，子脉冲数N=8， θ1=0、0.125和0.25 rad.从图7(a)容易看出，对于不同的 θ1，IML方法提供几乎相同的估计性能，且随着SNR的增加，目标AOA估计的RMSE越接近CRLB平方根. 此外，还易看出：当SNR＞20 dB时，目标AOA估计性能得到了明显的改善；SNR位于[20, 25] dB时，目标AOA估计性能改善相对比较平缓；当SNR＞25 dB时，目标AOA估计性能又进一步得到了较大的改善.

图7(b)给出了目标AOA的RMSE与CRLB平方根随SIR变化的曲线关系. 设定仿真参数为：SNR= 20 dB，子脉冲数N=8， θ1=0、0.125和0.25 rad.对于给定的SIR区间([−7, −3] dB)，从图7(b)可以看出，随着SIR的增加，目标AOA的估计性能改善并不明显. 例如，当SIR=−3 dB时，目标AOA估计的RMSE仅仅比SIR=−7 dB时目标AOA估计的RMSE改善了0.003 5. 因此，相比于SNR和子脉冲数N，SIR对目标AOA的估计性能影响很小.

图7 IML估计性能与CRLB平方根随SNR和SIR的变化关系Fig. 7 RMSE of the target AOA and the square root of CRLB vs. SNR and SIR

接下来，分析舰船目标与假目标AOA的差值Δθ(即舰船目标与假目标的分开程度)对目标AOA估计性能的影响. 图8给出了不同的 Δθ对目标AOA估计性能影响的仿真结果. 仿真参数设定为：SNR=25 dB，SIR = −4 dB， Δθ=0.25、0.375和0.5 rad. 从图8明显看出，随着 Δθ的增大，目标AOA估计性能下降了. 然而，在舷外有源诱饵干扰条件下，随着时间的推移，舰船目标和假目标分开程度会越来越大(即Δθ越来越大). 在这种条件下，尽管目标AOA的性能下降了，但对目标的AOA估计精度要求也同时降低了[20].

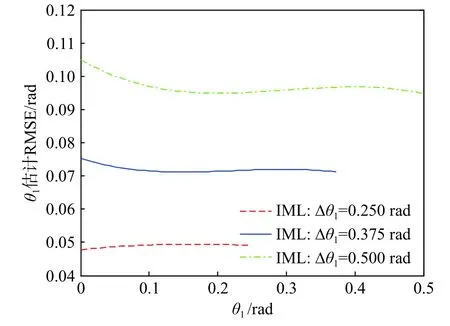
图8 不同Δθ对目标AOA估计性能的影响Fig. 8 Performance of the target AOA for various Δθ

最后，为验证本文所提IML方法和MM方法的估计性能，与文献[17]所提方法进行估计性能对比.考虑三组仿真数据：第一组数据仿真参数设定为N=4，SNR=20 dB，SIR=−4.8 dB；第二组数据仿真参数设定为N=8，SNR=25 dB，SIR= −4 dB；第三组数据仿真参数设定为N=12，SNR=30 dB，SIR=−3 dB. 不失一般性，在仿真实验中，假设相对RRCSγ是已知的.

为了验证本文所提方法的实时性，在计算机上测试不同AOA估计方法所需运行程序的时间. 对于每种方法，假设和、差通道的回波数据已生成，程序运行从处理回波数据开始计时，直到获得目标AOA结束，两者的时间差记为程序的运行时间. 笔记本计算机的配置为CPU主频1.8 GHz，内存8 GB. 进行10 000蒙特卡洛实验，并取程序运行时间的平均值. 在给定的三组数据中，表2对比了不同AOA估计方法的程序运行时间. 此外，图9给出了不同AOA估计方法的性能对比仿真结果.

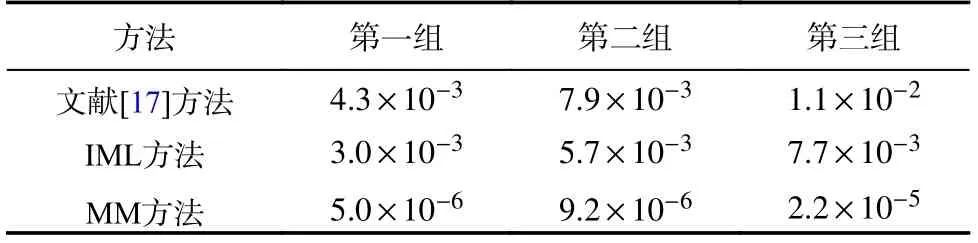
表2 不同AOA估计方法的实时性分析Tab. 2 Comparison of different AOA methods in real-time character s

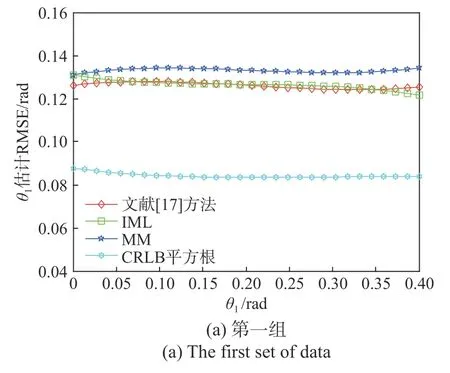
图9 三组数据不同AOA估计方法的性能Fig. 9 Estimation performance comparison among 3 different data set AOA methods

根据表2和图9，可以得出如下结论：

1)在不同的仿真参数条件下，IML方法和文献[17]所提方法几乎提供相同的估计性能，且IML方法的实时性比文献[17]所提方法提高了约29.3%，与理论分析结果基本吻合，这表明假设回波信号的同相和正交分量相互独立是合理的，它对目标AOA估计影响基本可以忽略.

2)在较低子脉冲数和SNR条件下，MM方法虽然比IML方法和文献[17]所提方法的估计精度略低，但实时性比IML方法和文献[17]所提方法改善了约三个数量级，且随着子脉冲数和SNR增加，MM方法能提供与其他两种方法几乎相当的估计性能.

3)随着子脉冲数N和SNR的增大，本文所提方法的估计性能越来越接近CRLB平方根.

综上所述，从估计精度和实时性两方面来综合考虑，本文所提方法比文献[17]所提方法的性价比更好. 此外，在实际应用中，根据估计精度和实时性要求的不同，可选择性地应用IML方法或MM方法来估计目标的角度.

5 结 论

在反舰应用场合，本文研究了单脉冲雷达导引头对抗舷外有源诱饵干扰的问题，提出了两种可选的目标AOA估计方法：IML方法和MM方法. IML方法具有估计精度高但计算量较大的特点，而MM方法同时兼顾了估计精度和计算复杂度，且随着子脉冲数N和SNR的增加，IML方法和MM方法的估计性能相当. 在实际应用中，若IML方法满足实时性要求和估计精度，则可选择IML方法；若无法满足实时性要求，则可选择MM方法来估计目标AOA.此外，通过蒙特卡洛仿真实验将本文方法与文献[17]所提方法以及CRLB平方根进行性能比较，理论分析和仿真实验表明，IML方法和MM方法比文献[17]所提方法的性价比更好. 值得指出的是，如何滤除海杂波是本文所提方法实际应用的关键条件，这将是下一步将要研究的问题.