两台机器上具有嵌套关系处理集限制的可拒绝排序
2022-03-06丁甜甜慕运动
丁甜甜,慕运动,柴 幸
(河南工业大学 理学院,河南 郑州 450001)
排序理论是运筹学组合最优化领域中一个重要的研究分支,主要研究工件(或称为任务)在机器上进行加工处理,如何优化不同的目标函数。例如尽可能快的加工完所有工件,实现时间表长的最小化。随着现代化的不断发展,越来越多的排序模型和相应的目标函数得到广泛的关注。近些年来计算机学家和运筹学家们对工件具有处理集限制或可拒绝的排序问题进行了深入的研究。首先,具有处理集限制的排序问题,是指由于工件属性和机器性能的限制,工件只能在对应的满足其属性的部分机器上加工。可加工某工件的机器的集合,称之为该工件的处理集。其中包含关系、树形关系、嵌套关系三类处理集限制的排序问题已经得到了广泛的研究[1]。其次,工件可拒绝排序是指工件可以不在机器上进行加工,即可以被拒绝(或者通过外包进行处理),此时需要支付一定的拒绝费用。
排序理论中的经典模型,m台机器上最小化时间表长(即所有工件的最大完工时间)的问题是强NP-困难的,不存在多项式时间的最优算法,因此此类问题的近似算法得到了广泛研究。近似算法主要讨论在合理有效的计算时间内得到较为好的近似结果,其优劣用最坏情形比来衡量。算法的最坏情形比,也称为近似比,是指对最小化目标函数的排序问题,在所有实例下,由算法所生成的目标函数值与最优的目标函数值的比值的上界。
工件具有处理集限制时最小化时间表长的排序问题已经得到了一系列的近似算法。Lenstra等人[2]对于具有包含关系处理集限制的排序问题得到了最坏情形比为2的多项式时间算法。紧接着Hwang等人[3]提出了关于解决上述问题的一个LG-LPT算法,该算法在m=2时的最坏情形比是5/4;在m≥3时最坏情形比是2-1/m-1,并证明了当m≥2时这个界是紧的.简单的来说这个算法就是把那些未排的工件中最长的放到可以加工它的等级最低的机器上。接着Glass和Kellerer[4]对于嵌套关系处理集限制的排序问题给出了最坏情形比为2-1/m的列表算法,并对包含关系处理集限制的排序问题给出了最坏情形比为3/2的算法。进一步Ou等人[5]对具有包含关系处理集限制的排序问题得到了最坏情形比为4/3+ε的近似算法,其中ε为任意小的正数。再有Huo和Leung[6]对嵌套关系处理集限制的排序问题给出了最坏情形比为7/4的改进算法,以及两台机器时最坏情形比为5/4的算法。
关于工件可拒绝排序问题也得到了若干近似算法。Bartal等人[7]对最小化时间表长加上总拒绝费用的排序问题给出了最坏情形比为2-1/m的近似算法。更多的相关研究可参见综述文献[8]。
1 问题描述
本文我们主要讨论的是两台机器上工件具有嵌套关系的处理集,同时工件可拒绝的排序问题。关于这个问题的描述如下:有n个工件的集合={J1,J2,…,Jn},和两台机器集合={M1,M2}。每个工件Jj都有加工时间pj和拒绝费用ej,以及它所对应的处理集。依据工件和机器的属性,每个工件只能在部分机器上加工,可加工工件Jj的处理集j⊆{M1,M2}。在本文中,我们讨论具有嵌套关系处理集限制的排序问题,任意两工件对应的处理集是相互包含或者不交的。因此工件的处理集有以下三类:{M1},{M2},{M1,M2}。此外,每个工件Jj都要面对一个问题,加工还是拒绝: 如果拒绝,那么需要支付拒绝费用ej;如果加工,那么就需要将Jj放到相应的机器上进行加工。我们的目标是使时间表长Cmax和总的拒绝费用RC之和最小。
2 算法及分析
我们把工件的拒绝费用ej与pj/2来进行比较(这里2对应总的机器数目),决定工件的拒绝与否,以及安排在哪台机器进行加工。因为这里是2台机器,而pj/2表示的是一个工件放到2台机器上的每台机器的平均加工时长,即对时间表长的最小贡献是这么多。如果此时拒绝费用ej 算法 首先对工件做预先处理,把处理集为{M1}或{M2}的工件放在序列前边,把处理集为{M1,M2}的工件放在序列后边;其次对序列中工件逐个安排加工,步骤如下: 步骤1对工件Jj,判断ej与pj/2的大小关系。 1)若ej 2)若ej≥pj/2,则转至步骤2。 步骤2依据Jj的处理集选择机器进行加工。 1)若Jj的处理集为{M1},则把Jj分配给M1进行加工; 2)若Jj的处理集为{M2},则把Jj分配给M2进行加工; 3)若Jj的处理集为{M1,M2},则把Jj分配给当前负载较小的机器(即当前已被分配的工件总加工时长较小的机器)进行加工。 为了更好地理解算法,我们先给出两个具体的实例,然后再给出算法的最坏情形比分析。 实例1 有3个工件,所满足的情况如下表: 表1 实例1工件详情 根据我们的算法,可以得出J1在M2加工;J3在M1上加工;J2拒绝。根据算法可得Cmax=8,RC=1。 而关于这个实例的最优排序是J1,J2,J3全部拒绝,故而有C*=0,RC*=6。所以有 实例2 有5个工件,所满足的情况如下表: 表2 实例2工件详情 根据我们的算法可得J1拒绝;J3,J4,J5在M1上加工;J2拒绝。故而可得Cmax=18,RC=0。 为了方便我们下面的分析证明,我们定义如下符号:对任一排序实例I来说,记由算法生成的排序为σ。在σ中,接收的工件集合记为JA,拒绝的工件集合为JR。其中Cmax表示排序σ的时间表长,即最大完工时间;RC表示排序σ中总的拒绝费用。实例I的最优排序记为π,在π中,接收的工件集合记为JA*,拒绝的工件集合记为JR*,其中C*表示排序π的时间表长;RC*表示排序π中总的拒绝费用。 为了我们分析的方便,我们做如下假设: 假设1由我们算法生成的排序σ的时间表长Cmax对应于M1的完工时间,即σ的时间表长Cmax是在M1上实现的。(若是在M2上实现的,可以把如下分析中的M1与M2互换即可。) 定理1算法的最坏情形比为2。 证明由假设1,设M1上最后完工的一个工件为Jh,且CH(Mi)表示在排序σ中机器Mi上的完工时间(i=1,2)。而Jh无非对应于以下两种情形:Jh对应的处理集为{M1,M2};Jh对应的处理集为{M1},此时说明M1上加工的工件全部都是处理集为{M1}的工件。 情形1Jh对应的处理集为{M1,M2}。由算法步骤2.3,Jh被分配给当前负载最小的机器,所以 下面分四种子情形分别讨论。 情形1.1排序σ与π接收的工件完全一样。即JA=JA*,JR=JR*。故RC=RC*, 情形1.2排序σ中接收的工件多于π中接收工件,即JA*⊆JA。此时π比σ多拒绝了一些工件,并且这些工件满足ej≥pj/2。用JA-JA*表示σ比π多加工的工件集合,记为Eσ。故而可得JR*-JR=Eσ,JA-JA*=Eσ。 情形1.3排序σ中接收的工件少于π中接收工件,即有JA⊆JA*。此时σ比π多拒绝了一些工件,并且这些工件满足ej 因此 情形1.4JA与JA*没有相互包含的关系,即排序σ中接收的工件与π中接收的工件不相互包含。此时σ比π多加工一些工件,用JA-JA*表示这些工件集合,记为Eσ,则它们满足ej≥pj/2;π比σ多加工了一些工件,用JA*-JA表示这些工件集合,记为Eπ,则它们满足ej 情形2Jh对应的处理集为{M1},说明M1上加工的工件全部都是处理集为{M1}的工件。同样此时也有以下4种子情形。 情形2.1排序σ与π接收的工件完全一样。即JA=JA*,JR=JR*。则Cmax=C*,RC=RC*。 情形2.3排序σ中接收的工件少于π中接收工件,即有JA⊆JA*。此时σ比π多拒绝了一些工件,并且这些工件满足ej 情形2.4JA与JA*没有相互包含的关系,即排序σ中接收的工件与π中接收的工件不相互包含。此时σ比π多加工一些工件,用JA-JA*表示这些工件集合,记为Eσ,则它们满足ej≥pj/2;π比σ多加工了一些工件,用JA*-JA表示这些工件集合,记为Eπ,则它们满足ej 综上所述,算法的最坏情形比为2,结合实例2可知所分析的这个近似比2是紧的。 在本文中,我们对两台机器上具有嵌套关系处理集限制的可拒绝排序问题进行了探讨。关于工件具有处理集限制或工件可拒绝的排序问题在以往得到了广泛的研究,也取得了若干近似算法,而这两者结合的排序问题在文献中很少提及。该类问题的难点在于如何结合不同工件的处理集限制与拒绝费用这两者的关系,合理的设计算法并尽可能取得较好的近似结果。本文中首次关于这类问题给出了最坏情形比为2的近似算法,通过实例可知该近似比的值是紧的。如何设计最坏情形比更小的近似算法,以及如何把两台机器上的相应结论推广到更为一般的模型上,会是非常有趣的挑战。

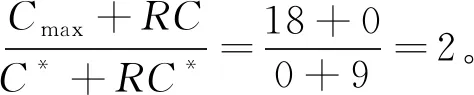
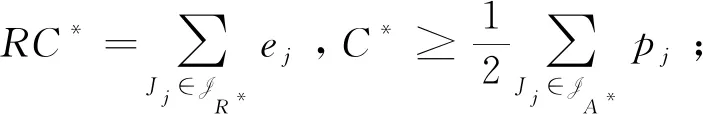
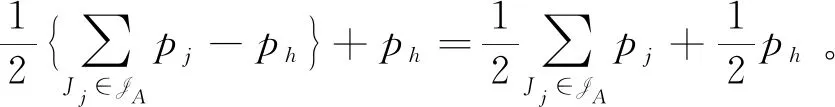
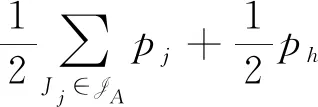


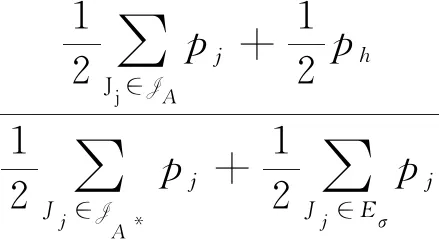
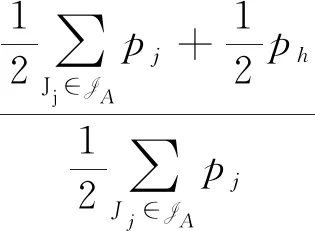

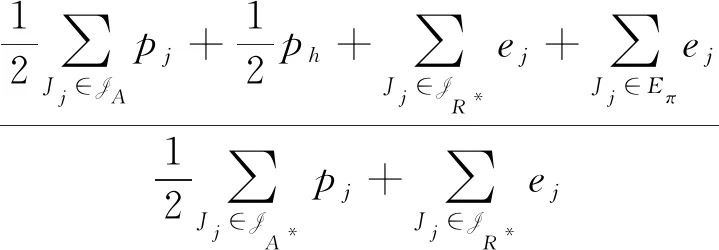
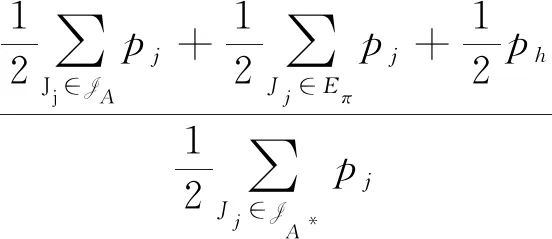
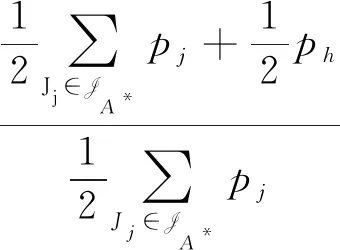

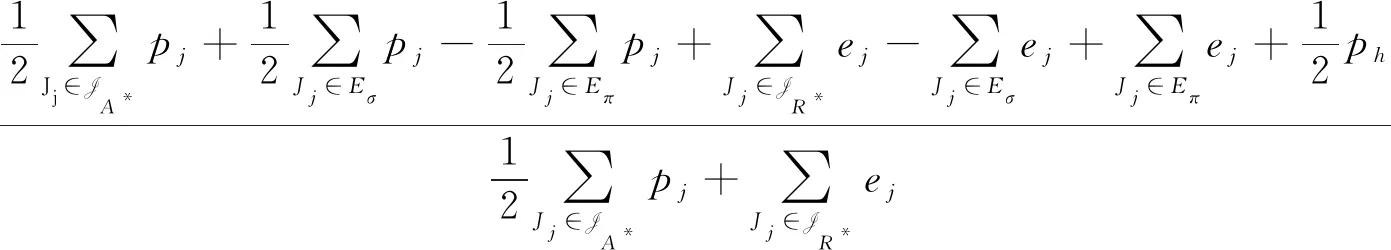
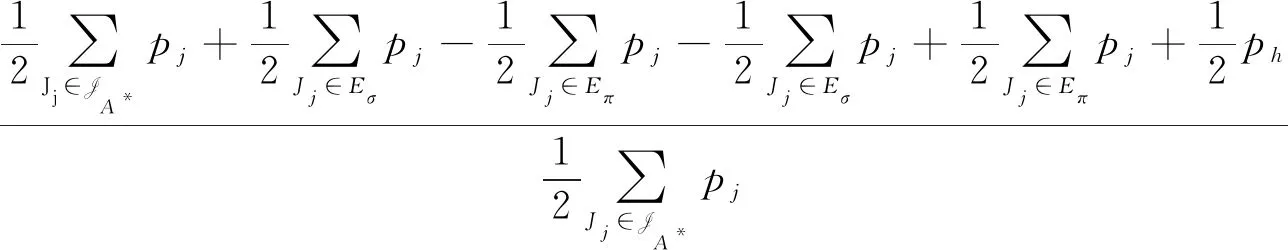
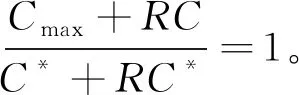


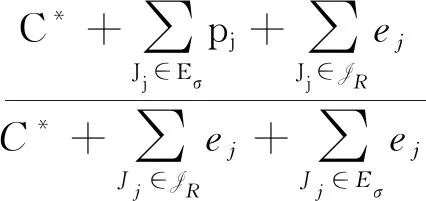
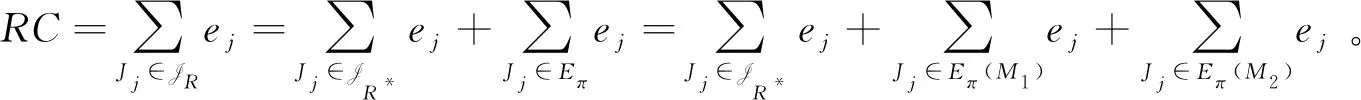
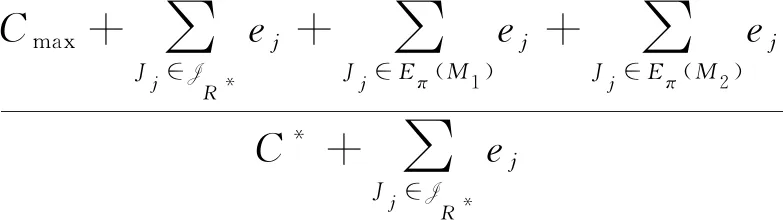

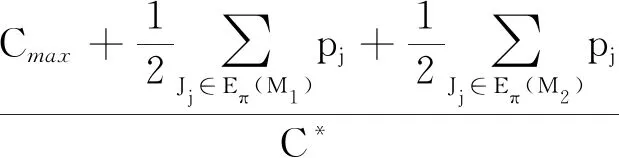
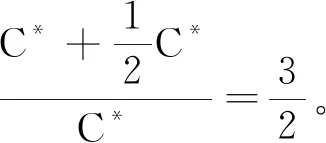
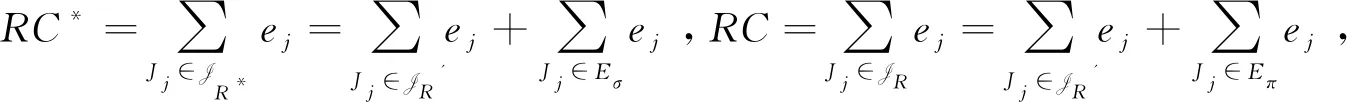


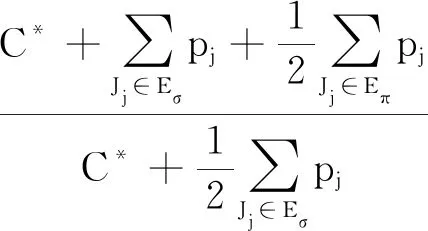
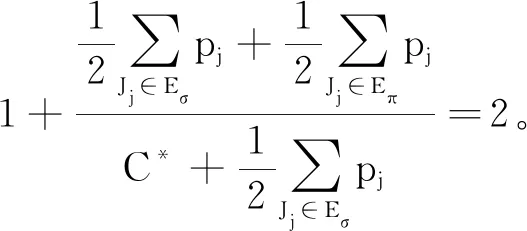
3 结论
