关注学生现有运算素养水平 实施有效数学课堂教学——以一道调研题教学为例

江苏省姜堰第二中学(225500) 凌世兵 徐树旺

对于数学运算素养，2017版课程标准从情境与问题、知识与技能、思维与表达、交流与反思四个方面给出了三个不同水平划分.多数学生的运算素养只能达到水平一，少部分学生能达到水平二.也就是大多数学生只能在熟悉的数学情境中，根据问题的特征形成合适的运算思路，少部分学生能够针对运算问题，合理选择运算方法，设计运算程序，很少有学生能够做到构造运算程序，解决问题.总有数学老师抱怨：我已花了很大力气从算法、算理等多方面来提升学生的运算素养水平，但收效还是不尽人意.究其原因，主要在于我们老师没有深入调研学生现有运算素养水平，不能从学生现有的运算素养水平出发，而是盲目拔高，讲自己所要讲而不是讲学生所要听，追求运算的高技巧与高难度，学生无法越级跟上，所以收效甚微，这需要我们老师调研并关注学生现有运算素养水平，基于学生现有的运算素养水平进行合理的教学设计，让学生拾阶而上，切实有效提升学生的运算素养水平.

案例已知函数f(x)=lnx+ax-1(a∈R).

(1)讨论函数f(x)的单调性;

(2)若函数f(x)图像过点(1,0)，求证：e-x+xf(x)≥0.

这是我校高二调研试题，第(1)小题是一个简单的分类讨论，学生均能完成，第(2)小题是难点，学生只能想到的是“要证e-x+xf(x)≥0，即证e-x+x(lnx+x-1)≥0”，然后直接构造函数g(x)=e-x+x(lnx+x-1)，再证g(x)≥0，但在解答过程中遇到了很大的困难，学生均未能完成证明.即学生只能在熟悉的数学情境中，根据问题的特征形成合适的运算思路，达成运算素养水平一，没有学生能够做到构造运算程序，解决实际问题，即不能到达水平二，这是学生的现有运算素养水平，老师须从这里出发帮学生解决困难，并力争在现有水平上有所提升.

任课教师A没有调研学生解法，而是直接讲解如下参考答案：

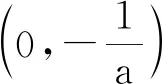
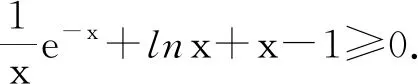
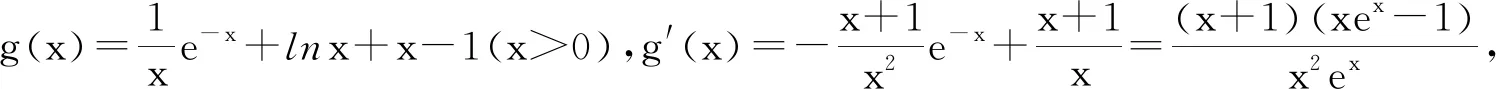
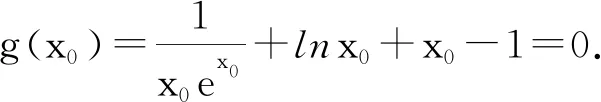
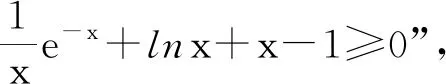
任课教师B先研究学生解法.

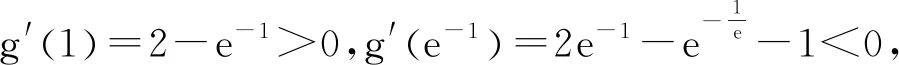
由于学生无法像参考答案提供的解法那样得到g(x0)=0，所以学生均未能完成解题，这是学生急需要解决的问题.教师B对这道题设计了如下的教学环节，首先帮学生解决“g(x0)=0”的困惑，然后再引领学生一起感受参考答案.

老师(投影学生解法)：要证g(x)≥g(x0)即要证g(x0)=0，但由于x0是超越方程e-x0=lnx0+2x0的根，无法解出，所以很大同学只能到此为止，很是遗憾！

学生1：从e-x0=lnx0+2x0得到g(x0)=0着实不易，但我试着把e-x0=lnx0+2x0代入g(x0)得到g(x0)=e-x0+x0(lnx0+x0-1)=e-x0+x0(e-x0-x0-1)=(1+x0)(e-x0-x0)，这里出现了两个因式，显然我们要证e-x0-x0=0，可我未能成功.

沿着学生1的思路，再从“e-x0=lnx0+2x0”寻找路径，经师生合作得到如下解答：

由①式可得e-x0-x0=lnx0+x0.设e-x0-x0=lnx0+x0=t，则 e-x0=t+x0,lnx0=t-x0，即-x0=ln(t+x0),lnx0-t=-x0，可得lnx0=ln(x0+t)+t， 由此同构式可得t=0， 则 e-x0-x0=0，所以 g(x0)=e-x0+x0(lnx0+x0-1)=e-x0+x0(e-x0-x0-1)=(1+x0)(e-x0-x0)=0，所以 g(x)≥g(x0)=0 .

实际上，学生在考场上的解法得到g(x0)=0着实不易，这对代数恒等变换提出非常高的要求，难怪学生均未能完成解答，在师生通力合作下，问题终于得到成功解决，学生课前的困惑得到了圆满解决，甚是欣慰，虽解决地很是辛苦，但拉近了师生、生生之间的距离，课堂和谐高效.这样的过程在考场很难完成，为了回避这一思维难点，所以此题提供的参考答案在原有不等式两边同时除以x，但如果不看参考答案，估计老师也会像学生那样移项直接构造函数，当然，部分解题经验较丰富的老师还是会选择参考答案的思路.

紧接着B教师给出了参考答案，并与学生一起进行了比较与分析，得出如下小结：在原有不等式两边同时除以x后，所构造函数的导函数只含有一个超越表达式，易于得出导函数的零点；而直接构造函数的导函数含有两个超越表达式，很难得出导函数的零点.学生心中的结得到了彻底解决，收获满满！

学生2(举手)：老师，我有个新的解法.在原有不等式两边同时乘以ex，然后构造函数g(x)=1+ex(xlnx+x2-x)，其导函数为g′(x)=ex(x+1)(lnx+x)，由g′(x0)=0可得lnx0+x0=0，即lnx0=-x0，同样可得x0=e-x0，接下来同前面解法，问题也能得到圆满解决.学生2的解法中，所构造函数的导函数含有两个超越表达式，但一点都不影响问题的解决，由此可见，前面的小结也不是绝对的，学生2能由“除”想到“乘”，并很快给出新的解法，敢于突破老师超越老师，这说明在教师B正确课堂教学设计的影响下，学生的数学运算素养水平得到了极大提升，这是有效课堂教学的充分体现，也是B教师合理教学设计的有力证明!

B教师虽然浪费了教学时间(只讲了这道题和两道变式)，未能像A教师那样完成更多的教学任务(完成整份调研测试6道重点试题的讲评)，但其收效却很大，要知道，在课堂教学中，像B教师这样的讲解才是学生最需要的，当然也是很有效的.

当然，课后经听课老师们深入研讨后发现：在函数的综合题中，经常会遇到令人望而生畏的超越不等式，在艰难求解后，可基于文[3]的思考进一步探索出此题的命制路径.

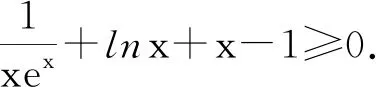
结语：由于上课教师A课前没有认真研究学生的解答过程，直接讲参考答案，还在暗地里嫌学生笨，连“不等式两边同时除以x”都想不到，但学生非常期待老师能帮其完成解答，但教师A只提供了一个学生不能想到的思路，技巧性强，学生根本达不到，这样的课堂教学效果是很差的，我们需要切实解决学生的问题，达成有效课堂，真正提升学生的运算素养水平.任课教师B课前充分研究学生解法，先展示学生未能成功的解法，并与学生合作完成后续思路，后再提供新的思路，最后进行比较，以总结此类问题的常用处理策略，即教师B先基于学生现有运算素养水平，后再提升学生运算素养水平，达成了很好的教学效果.

学生解法是学生现有数学运算素养水平的真实体现，即可理解为学生的“最近发展区”，是学生数学运算素养水平生长的起点，也就是老师课堂教学的起点及着力点，课堂教学应始于此起点，首先抓牢这一起点，然后带领学生飞向更高的点，所以我们老师要讲学生所要学，而不是讲老师所要教，基于学生现有数学运算所以水平，实施切实有效的教学，真正帮助学生提升数学运算素养水平，让数学核心素养落地有声.