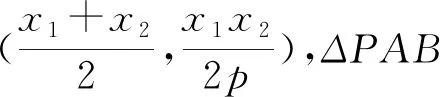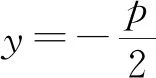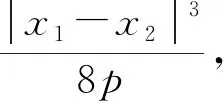数缺形时少直观，形缺数时难入微——2021年全国乙卷理21题的探析与拓展

江西师范大学附属中学 (330027) 张 璀

1 试题呈现

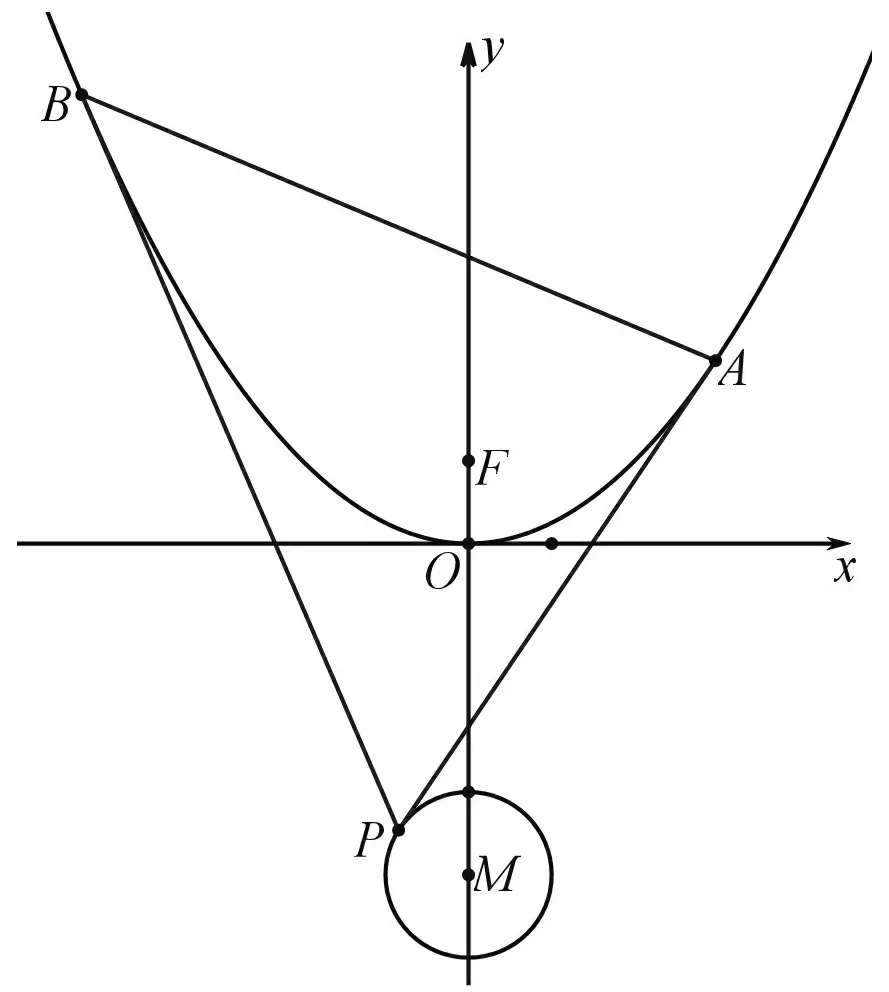
图1

(2021年全国乙卷·理科第21题)已知抛物线C：x2=2py(p>0)的焦点为F，且F与圆M：x2+(y+4)2=1上的点的最短距离为4.如图1

(1)求p；

(2)若点P在M上，PA,PB为C的切线，切点为A,B，求ΔPAB面积的最大值.

2 解法探究

该题形式上以抛物线中的阿基米德三角形为背景，结构虽简单、明了，但内涵丰富、综合性强、解法灵活，考查了抛物线和圆的简单几何性质，直线与抛物线的位置关系、三角形的面积等知识，考查了学生分析问题、解决问题的能力及转化与化归的数学思想，体现了逻辑推理、数学运算、直观想象等数学核心素养.第(1)问属于常规问题，答案是p=2，第(2)问是一道求三角形面积最大值问题，内涵丰富，本文主要对该问予以探析与拓展：

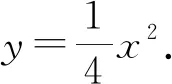
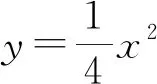
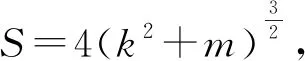
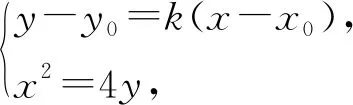
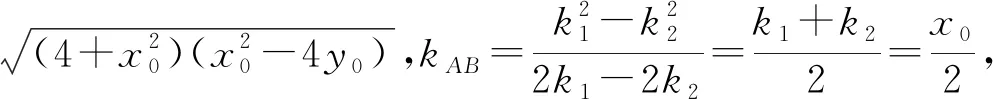
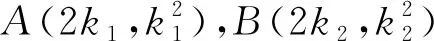
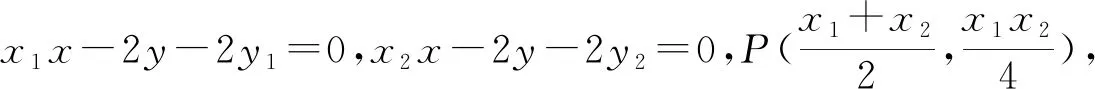
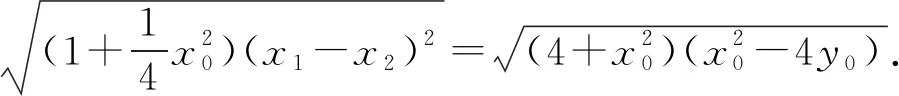
评注：该法也属于同构方程法，区别于解法2同构的元素为斜率，解法3同构的元素为坐标，利用“两点确定一条直线”的原理，得到直线AB方程为x0x-2y-2y0=0，两种不同的同构法，异曲同工之效.

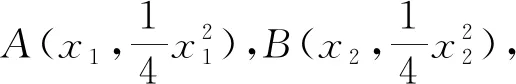
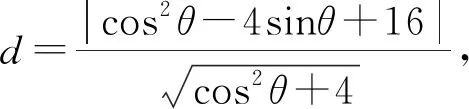
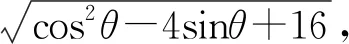
评注：该法通过引进三角函数设参数方法，将直线AB的方程及ΔPAB面积的给表示出来，相比前几种方法更好地简化了运算量，这一类方法尤其是在研究直线与椭圆的位置关系中优势比较明显.

3 变式训练

变式1 已知抛物线C：x2=4y，P为直线y=x-2上一点，PA,PB为C的切线，切点为A,B，求ΔPAB面积的最小值.

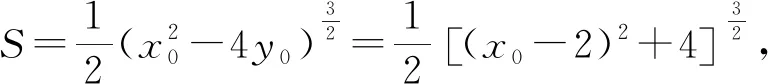
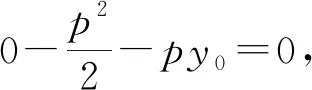
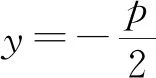
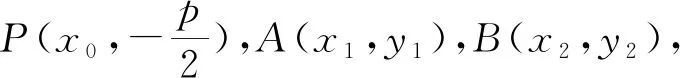
4 一般化拓展

已知抛物线C：x2=2py(p>0)，C上两不同点A,B的坐标分别为(x1,y1)，(x2,y2)，以A,B两点为切点的切线交于点P，通过以上探究，我们不难得到阿基米德三角形PAB的如下性质：