中考数学命题的几类失误分析与思考

四川省成都市第十二中学 (610041) 邓万强四川省成都市第十八中学 (610072) 向 城内江师范学院数学与信息科学学院 (641100) 刘成龙

中考是九年义务教育阶段最重要的一次考试.自然而然，中考命题成为了一项艰巨而严肃的工作，它不仅对命题者学科素养要求较高，而且对逻辑关系、书面表达、心理素质等要求较高.因此，中考命题偶尔会出现失误.本文中分析中考数学命题中的常见失误，以期对命题工作的优化有所帮助.

一、中考命题失误的几种类型

失误1.数据设置不当

由于命题者所设置数据不当，导致得出的结果与基本事实、定理、公理等不相符合，造成命题失误.

案例1已知圆锥的底面半径为20，侧面积为400π，则这个圆锥的母线长为.(2018年齐齐哈尔)

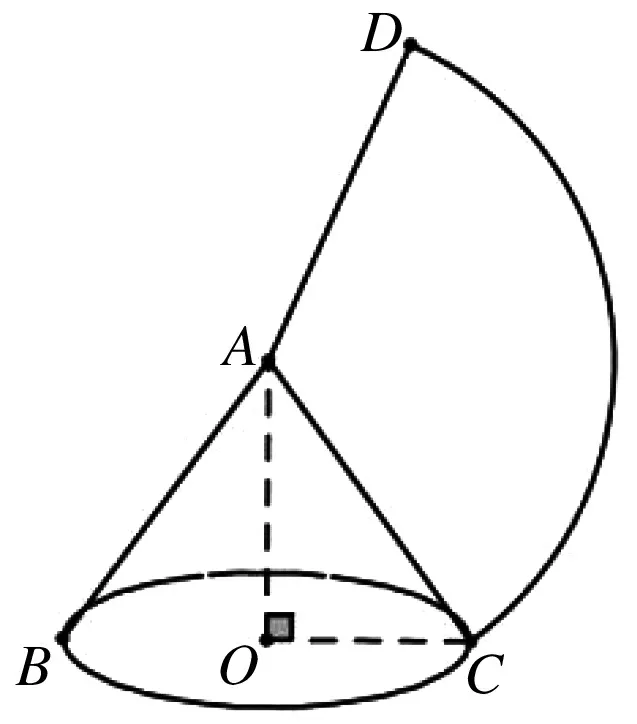
图1

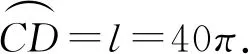
评析：利用所给数据OC=20，得到RtΔAOC中斜边AC与直角边OC相等.违背了三角形中大边对大角，小边对小角这一基本事实.

失误2.图形绘制不准确

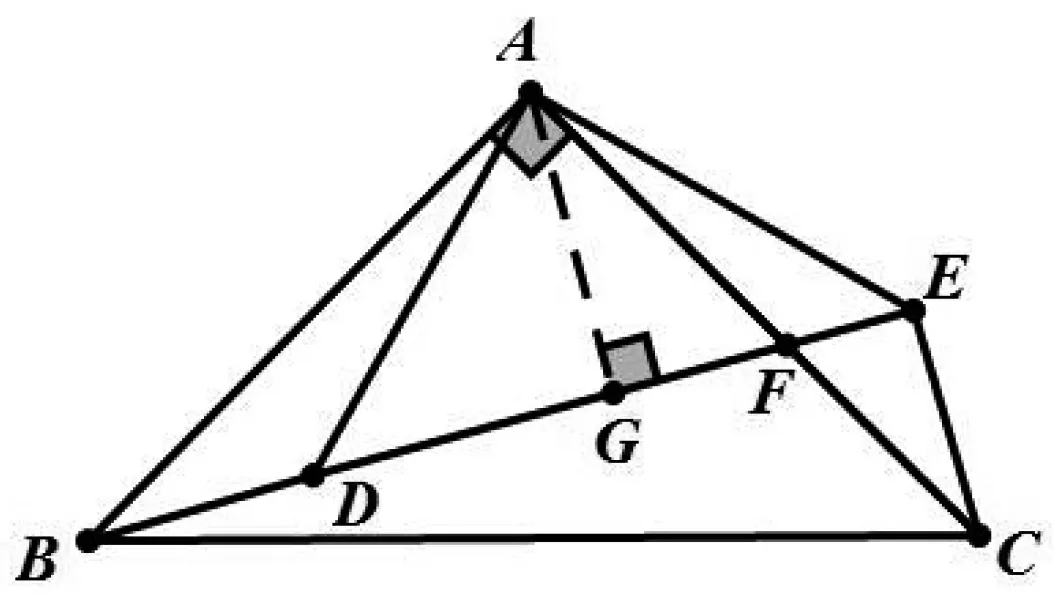
图2

案例2 如图2，在ΔABC中，∠BAC=90°，AB=AC=10cm，点D为ΔABC内一点，∠BAD=15°，AD=6cm，连接BD，将ΔABD绕点A按逆时针方向旋转，使AB与AC重合，点D的对应点为点E，连接DE，DE交AC于点F，则CF的长为cm.(2019年山西)

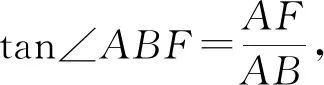
评析：错解的原因是学生误以为B、D、E三点在同一条直线上，其根源是所给图形不准确.这与美国著名的数学问题解决专家匈菲尔德提出的一个好的题目应满足的5个条件中的“不故意设陷阱”相违背.

失误3.设问表述不当

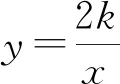
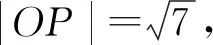
评析：本例中的k不存在，但题目设问是：“则实数k=”，显然设问欠妥.

失误4.条件互相矛盾

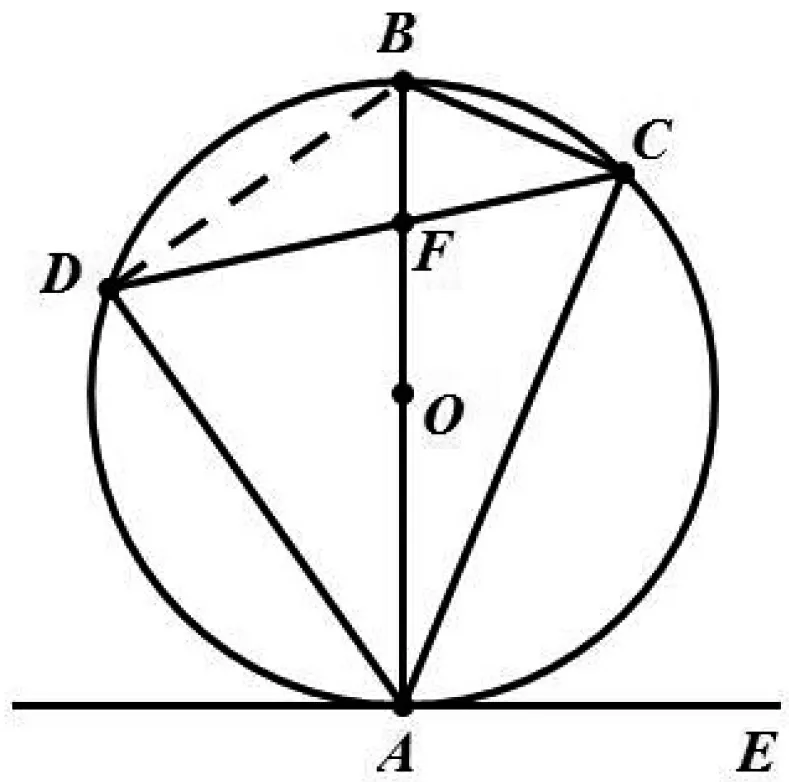
图3

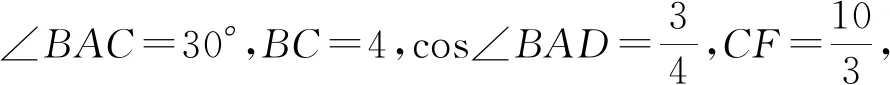
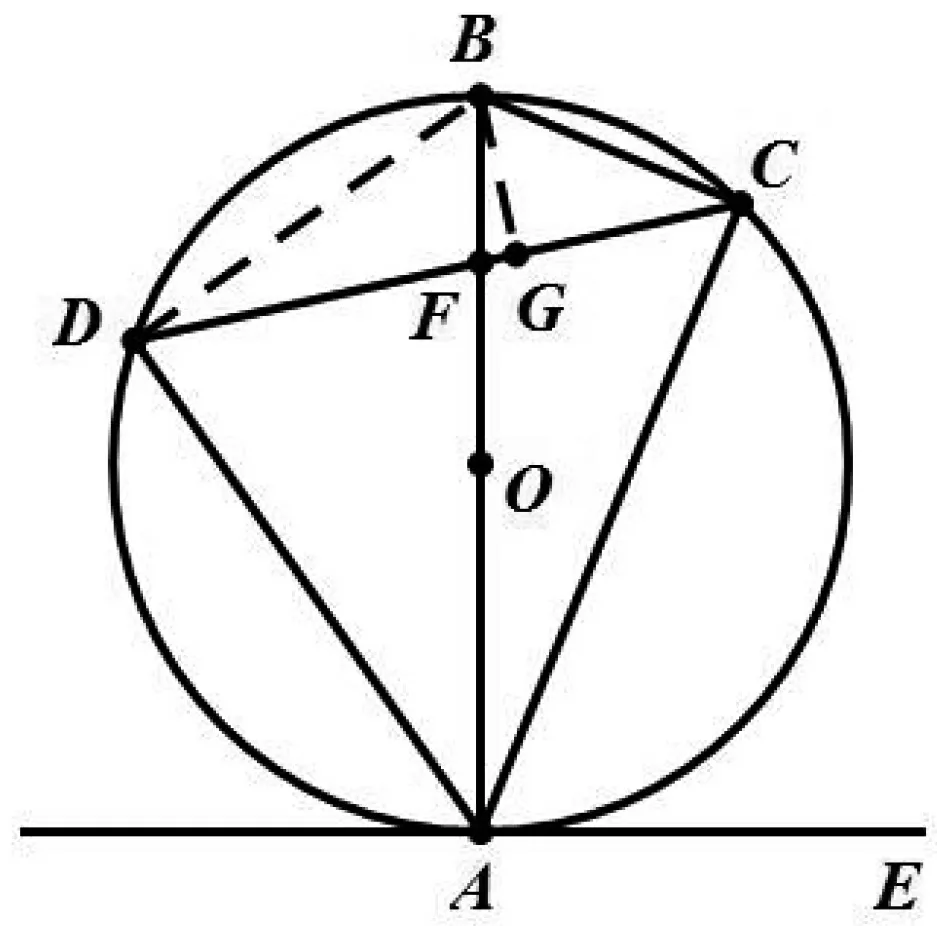
图4

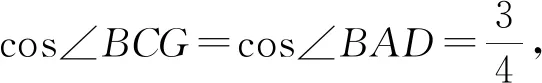
失误5.难度设置过大

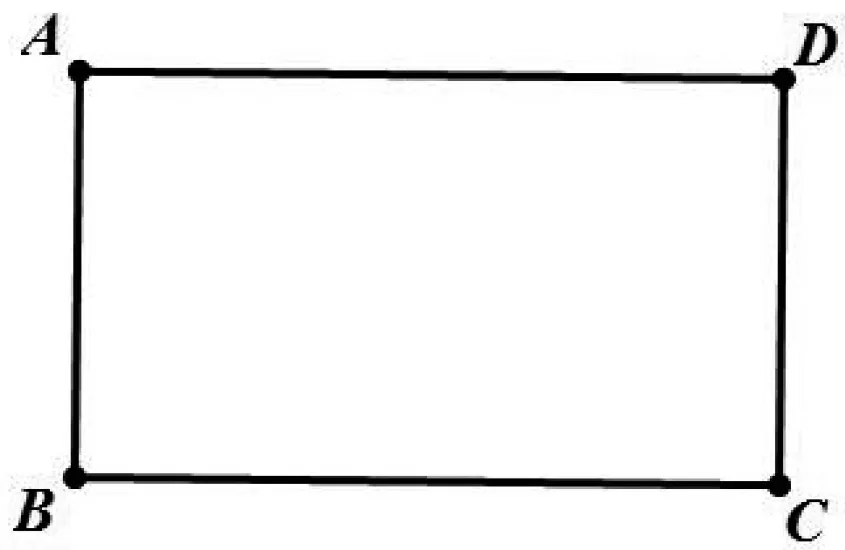
图5

案例5 如图5，有一矩形纸片ABCD，AB=8，AD=17，将此矩形纸片折叠，使顶点A落在BC边的A′处，折痕所在直线同时经过边AB、AD(包括端点)，交AB于E，AD于F，则折痕EF的取值范围为.(2014年达州中考改编)

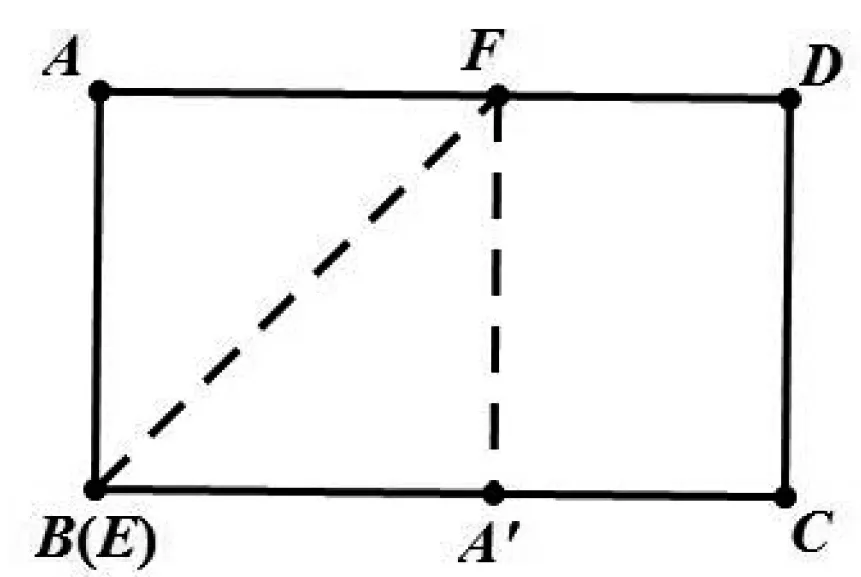
图6

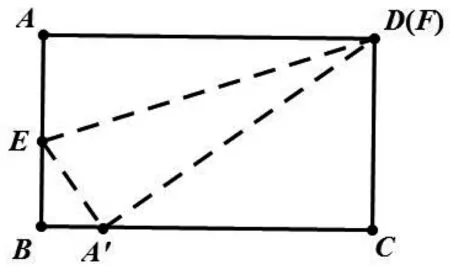
图7

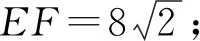
评析：错解是通过几何关系计算出特殊位置的线段长度，得到折痕的范围，看似天衣无缝.事实上，本例难度较大，超出了初中学生的能力范畴.

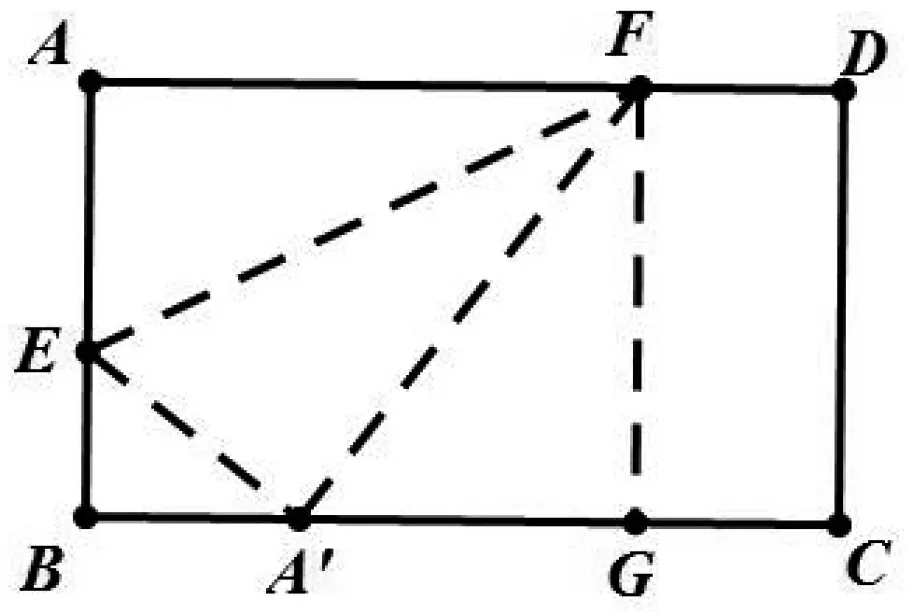
图8

失误6.试题背景不公

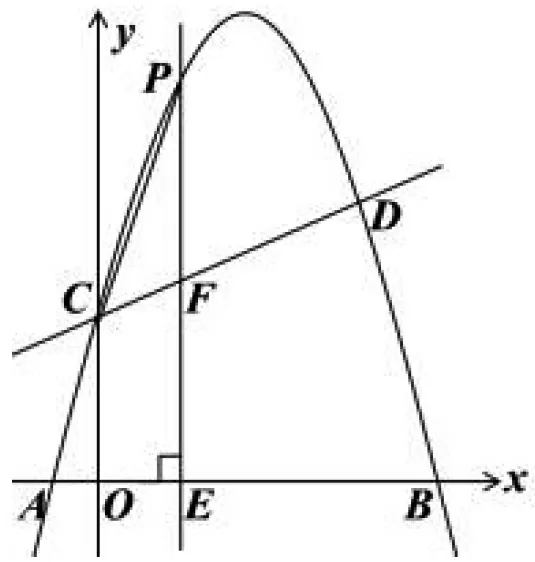
图9

(1)求抛物线的解析式；

(2)若点P的横坐标为m，当m为何值时，以O、C、P、F为顶点的四边形是平行四边形？请说明理由；

(3)若存在点P，使∠PCF=45°，请直接写出相应的点P坐标.(2013河南中考)

评析：本例(3)含有高中夹角公式的背景.运用初中知识解答本例需构造直角三角形，再利用三角形相似和勾股定理来解答，涉及较繁琐的运算.但借助高中的夹角公式来解答可以回避构造、避免繁琐的运算，从而大大降低试题难度.毫无疑问，对于那些学习了竞赛数学或老师讲过夹角公式的学生来说占尽优势，显然背景不公平.特别指出，中考命题必须坚持试题背景公平，即试题背景对所有人都是公正中立的，不会对某个或某些特定的群体产生与考试目的无关的过激反应.

失误7.照抄照搬陈题

图10

(1)求证：BC是⊙O的切线；

(2)连接AF，BF，求∠ABF的度数；

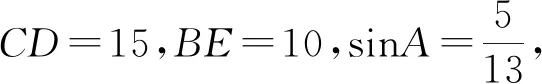
评析：本例是2012年中考试题，但某地命题者将该题目一字不差地搬上了2015年中考试卷，显然试题的信度和效度大大降低，更为不幸的是本例是一个错题，相当于命题者抄袭了一个错题.无论是从学术的视角，还是从中考的重要性和严肃性来讲照抄照搬都应该杜绝.笔者认为中考命题可以借鉴现有中考试题，但需要适当改编.

二、对命题的思考

试题命制是一个严肃而充满创造的系统工程，既要关注知识、能力、素养的考查，又要注重合适的难度、有效的信度和适当的区分度的设置，更要关注试题的严谨性.[1]道尔顿指出，一个好题必须具备下列条件中的一个或更多：问题要简单，是学生能认识并解决它；依靠学生的知识和能力能得出多种解法；能引导学生转向类似的问题；包含的数据能够被理解、分类、列成表格和分析；能够通过模型和简图解决；能马上引起学生兴趣；通过学生现有知识或将要学到的知识能将一种解法一般化；能用一种再认知的方式解决；答案要有意思.同时，匈菲尔德给出了好题的五条原则：容易接受的(不需要大量技巧)；有多重解题方法(或者至少有多重思路)；蕴含了重要的数学思想；不故意设陷阱；可以进一步开展和一般化(导致丰富的数学探究活动).这些条件和原则为试题命制提供了方向和要求，同时也对命题者的素养提出更高的要求.