例谈哲学观念对数学学习的影响及其教学启示
2022-03-05泰州学院225300杨俊林
泰州学院 (225300) 杨俊林
爱因斯坦指出,哲学可以被认为是全部科学之母.哲学探究的是所有事物的一般性规律,是对自然知识、社会知识与思维知识的概括与总结.哲学的观点是高度抽象的,它不涉及具体的学科,但它对具体学科的研究与学习乃至于一个具体问题的求解都有指导作用.人们的一切行为是受意识支配的,而支配行为的意识是人们所处的社会关系及外界其他因素作用于人脑的结果.数学家的“数学研究总是在某种哲学思想的指导下进行的”[1],学生的数学学习行为也受意识的支配.教学过程中常常发现,支配学生数学学习行为的意识更多的是教师作用于学生的“解题套路”,缺乏科学性、创造性,以至于相当多的学生学习过十多年的数学,进入大学时最基本的数学方法却忘得一干二净.如果将哲学原理的教学与具体学科的学习结合起来,使相应哲学观念真正内化为支配学生学习行为的意识,那么学生的数学学习就能在正确的思想指导下进行.从而真正达到提高学生核心素养的目的.
1.运动的规律性观念与解题策略的形成
例1已知实数a,b,c成等差数列,点P(-1,0)在动直线ax+by+c=0上的射影为点M,若点
N(3,3),则线段MN的长度的最大值是多少?
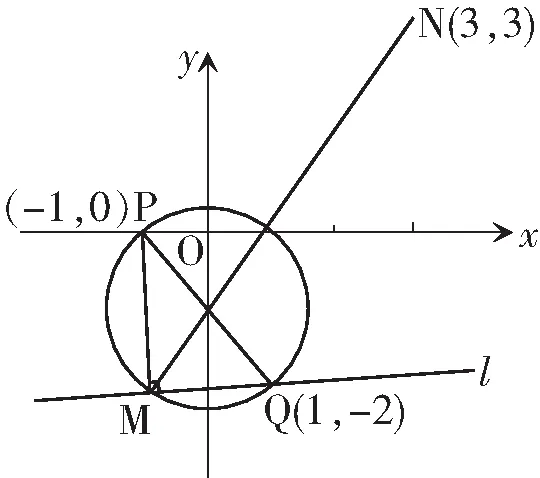
图1
分析:本题最大的思维障碍是“动直线ax+by+c=0在图形中如何表示?”直线是“动”的,它会毫无规律地“动”吗?“运动的规律性”意识的导向作用是引导解题者探索动直线的运动规律.由于动直线的系数是a,b,c,而a,b,c成等差数列,令公差为d,则动直线方程可改写为“(b-d)x+by+(b+d)=0”,再从“平行移动”“过某定点”的角度观察动直线的运动规律.从哲学的角度看“主元”有其“相对性”.如果将b,d视为主元x,y为常系数,方程又可改写为b(x+y+1)-d(x-1)=0.不难发现动直线过点(1,-2).这样问题就转化为“直线l过Q(1,-2),P(-1,0)点在l上的射影为点M.若点N(3,3),则线段MN的长度的最大值是多少?”.
显然,点M为以PQ为直径的圆上动点,MN的最大值为MN过圆心时(M,N在圆心的以异侧)线段的长度.
教学启示:中学哲学课中也会讲运动的规律性,但由于其立足点是较为“抽象”的客观现实世界而无法深入到具体学科领域,因而很难获得学生的理性认同.而数学教师在解题教学过程中过于程式化导致数学学习停留在操作层面难以转化为学生的“核心素养”.数学中变量的运动变化是哲学中运动规律的具体化,只要数学教师点拨得当,学生很容易提高数学解题活动中思维的“阶”.在解题教学中引导学生坚信规律的存在,感受根据发现的规律解决问题带来的乐趣,则容易使“运动的规律性”观念扎根于学生的认知世界,并在新问题的解决过程中发挥着积极的作用.


教学启示:在教学中,只要涉及运动的对象,如“动点”“动直线”“动圆”等,都应努力唤醒学生的“运动的规律性”意识,从而在这一意识的驱使下努力探求“运动对象”的“变化规律”.找到了“运动对象”的“变化规律”,自然就找到了解决问题的方法.
2.特殊与一般观念下的函数单调性探究
辩证唯物主义认为矛盾具有普遍性与特殊性,矛盾的普遍性和特殊性在不同的场合可以相互转化,可以从特殊性中概括出普遍性,也可以在普遍生的指导下研究特殊性.其相应的数学观念一般指“抽象意识”与“化归意识”.在中学数学教学中相当多的数学知识教学可以有意识地运用数学思想方法加以引导,在学生学习数学知识的同时获得数学思想提升数学观念,形成科学的哲学观.
例3 “函数的增减性”与“导数及其应用”的教学[2].
湖北省潜江市园林四中的戴老师提供的“关于如何确定函数单调区间的端点时的方法”就很有代表性.
首先学生思考后给出了求一类函数单调区间端点方法,但觉得理由不够充分,其方法如下:
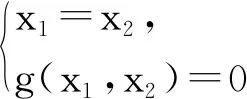
接着教师在对学生发现的结论进行肯定的同时引导学生说出发现的过程.原来该生是从一个很特殊的函数f(x)=x2-2x+3入手进行探究的,其过程如下:

该生就是在此基础上给出了一般性的结论.教师充分肯定了学生的做法,同时告诉学生其中蕴含的道理在后面学习微积分的知识时就会明白.
教学启示:显然上述案例中学生就是在“矛盾的普遍性与特殊性”的“潜意识”下开展的数学探究活动,十分值得推崇.然而,从实际教学的现状看,这样的例子却不多见.在日常考试中不少选择与填空题只需要学生根据特殊与一般的关系用特殊值代入即可,但学生想不到;综合题中可以借助特殊性寻找解决问题的一般策略,但学生往往也想不到.原因出在哪里呢?出在教学,在实际教学中,哲学课老师不举学科的例子,学科老师不注重“学科观念”的教学.以数学学科为例,相当多的教师关注的是较低层次的数学解题教学,较少关注“数学观念”的教学.一般认为数学思想方法被划分为四个层次:“解题术”“解题方法”“数学思想”“数学观念”,而“数学观念”是认识世界的“哲学思想”,数学观念“直接影响着数学中的发现、发明与创新法则形成的共同预设或元知识层次”.[3]
上面的例子在后面学生学习“导数在研究函数中的应用”时仍可借鉴:

在数学教学中关注哲学观念的渗透其本质是追求数学观念的养成教育.在大力倡导数学核心素养教育的今天,不少教师仍然不注重数学知识形成过程的教学,总是以最短的时间最快的速度讲完相应知识点,过于关注解题的套路与技巧,忽视了对数学本质的认识过程.数学科学本身可以视为一个“生命体”,有其自身“生长”的规律,只有关注数学观念的养成站在哲学的高度引导学生自主构建数学认知结构,才能真正回归数学教育的本源.
3.局部与整体、无限观念下导数概念的学习
哲学上关于无限的观念集中于潜无限与实无限的思辨上.所谓潜无限是将无限看作一个永远没有穷尽的,潜在的过程.所谓实无限是把无限对象看成是可以自我完成的过程或无穷整体[4].历史上哲学家们对无限的认识也不全面,古希腊时期的哲学家没有将无限单独作为一个名词,以为“无限物体”不存在,而是作为副词,无限与过程相联.Aristotle只承认潜无限,拒绝实无限[5].无限观与数学是密不可分的,希尔伯特认为“数学是研究无穷的科学”[6].学生对数学中的无限的认识有利于理解数学概念,同时也有利于提高无限认识能力[7].学生关于无限观的形成也将直接影响其对数学的领悟.
例4 学生对导数概念的理解情况调研.
考虑到中学生的理解能力,新课标在引入微分初步知识的同时又删除了形式化的定义,目的是让学生借助“微积分的教育形态的表现形式”把握微积分的实质.导数的意义其本质在于“函数在一点可导,意味着这个函数在这一点附近近似于一次函数”“研究函数在某一点可导不只看一点的值,要考察这一点周围的无限小局部性态”“导数之美在于体现局部的‘率’,这是一个无穷的过程”[8].而实际教学效果却不尽如人意.房元霞等人的调研发现仅34.42%的高三学生将导数理解这“函数在某点的瞬时变化率(平均变化率的极限)”,仅22.12%的学生将导数理解为“函数曲线上某点切线的斜率”,而真正理解为“缩到一个点附近来研究函数”的仅0.96%;而对数学本科(大二)学生调研发现,仅21%的学生能表达导数的经济学意义,57%的学生能用导数近似表示函数在某点的值[9].郭玉峰等在对师范院校学生导数内容理解情况调研时也发现“深入理解不够,如部分学生尽管知道导数基本概念,但理解还只限于表面,缺乏深层次的理解”[10].
教学启示:一要正确解读教材,渗透局部代替整体的思想.微分学缘于“在研究物体的运动时要求出它在任一时刻的速度和加速度,或者在研究光线通过透镜的规律时要求出光滑曲线上给定点的切线和法线,以及在研究炮弹的射程时要求出函数的最大值和最小值等”[11].在人们没有找到合适的方法时最原始的想法就是“取近似值”,或者说是“以直代曲”,用“局部代替整体”.苏教版教材无论是关于研究曲线上一点处的切线还是研究运动物体的瞬时速度都在力求表达“某点(某时刻)附近哪条直线(哪个常数)更加逼近曲线(瞬时速度)”,如果认识不到这一点,教学就会出问题,而认识到了这一点,就会自觉地将“局部特征代替整体特征”的思想渗透到教学中,对学生理解导数的本质大有裨益.
二要重视学生关于“无限观”的形成.其实关于无限的思想学生在小学阶段就有所了解,如“无限循环小数”“无限不循环小数”“射线”“直线”等等.初中阶段也会涉及到,如方程组有“无穷多组解”,数轴上有“无穷多个点”,在研究一次函数、反比例函数、二次函数时也会涉及到“无限增大”“无限减小”等等.高中数学中这样的例子就更多,但数学教材中对“无限”往往采取“避而不谈”的方式,数学教师在课堂上对“无限”也不深究,导致学生难以形成关于“无限”的正确观念.然而“数学是研究无穷的科学”,数学中的很多概念蕴含着“无限”的思想,如“平行线” “无理数” “极限” “函数” “单调性” “奇偶性” “连续” “导数” “积分”等,如果没有正确的“无限观”是很难正确把握这些概念的,如果这些概念没有能真正内化为学生的个人知识,对其后续学习影响是很大的.在导数概念的教学中无论是研究曲线有某点的切线还是运动物体在某时刻的瞬时速度都包含了一个“无限接近”的过程,在形成导数定义时更加突出了“△x无限趋近于0”,这个过程是无限的.尽管考虑到学生的认知能力,不宜用严格的数学语言进行精确刻画,但课堂教学过程中教师还应重视引导学生充分感受“无限过程”,不但要告知无限过程是 “潜无限”,而且要明确最终状态是“实无限” .
三要帮助学生整体认知数学概念.学生无限思辨的自发方式是潜无限,实无限是后天发展而来的[12].实无限隐藏在数学概念中,需要学生深入思考才能掌握.如“函数单调性”概念中,“任意的x1,x2”即是从整体的角度描述了自变量取一切值的情形.而“任意”一词却蕴含了“无限”的思想.在导数概念的教学中如果从“一尺之棰,日取其半,万世不竭”角度帮助学生领会:“日取其半”是一个动态的过程,但总归是“一尺之棰”这一完整的结果,则对学生理解函数在某点的导数值是十分有益的.也可以借助芝诺悖论中的“阿里奇追龟”帮助学生理解,通过“阿里奇无限接近乌龟”与“阿里奇追上并超过乌龟”来深化对潜无限与实无限的理解.
4.偶然性与必然性相统一观念下的概率与统计知识的教学
上个世纪八十年代以来,“把统计和概率的初步知识作为数学基本修养的一部分而引入中学甚至小学课程”[13]足见概率与统计思想作为公民数学素养中的重要部分十分重要.然而,学生真正能够获得统计与概率思维方式依然离不开偶然性与必然性相统一观念的指导.
例5 今天的天气预报不准确.
“今天的天气预报不准确”往往会出自受过高等教育者之口.这似乎不应该“大惊小怪”,然而这反映了一个问题,即中学数学教育的目的达成问题.义务教育阶段数学课程标准指出“义务教育阶段的数学课程是培养公民素质的基础课程”,第三学段的课程目标中有“进一步认识随机现象”“感受随机现象的特点”的表述[14].高中数学课程标准中更是将“数据分析”能力作为核心素养明确提出[15].但概率与统计知识最核心的思想是随机思想与统计推断思想,其相应的哲学观念是“现实世界中的任何事物、任何过程都具有必然和偶然的双重属性.必然性是通过大量偶然性表现出来的”[16].今天下雨还是不下雨是一种随机现象,但通过对气象的观察人们发现了气象的发展变化规律在此基础上作出“下雨的可能性推断”,如果今天并未下雨这也是一种随机事件,如果借此说明天气预报不准确,这就偏离了对气象预报的本质,说明人们还不具备对随机现象认识方面的基本素养.
教学启示:概率统计的教学要教方法,更要引导学生感悟思想.将概率统计知识纳入中小学数学课程是新课程改革的一大亮点.但如何实施这一内容的教学值得广大教师深入探究.这部分内容知识点多,相关数学方法也多,教学难度较大,因此在实际教学中我们往往过多注重具体解决问题的方法与问题模型而忽视了培养学生的随机性数学思维[17],导致会做概率统计题但无法解释随机现象. 例如,小学阶段学生就掌握了抛一枚质地均匀的硬币,正面与反面朝上的可能性都是二分之一,但当问及抛一枚质地均匀的硬币五次都是正面朝上,那么抛第六次是正面朝上的可能性大还是反面朝上的可能性大,回答可能性一样大的中小学生为数不多.这说明学生还未掌握随机性数学思维意识.再之,教学中应时刻关注“偶然性与必然性相统一”这一哲学观念的渗透.关于概率统计内容的教学往往是从随机现象引入,在让学生感受一系列随机现象的同时务必提醒学生“偶然性中一定隐藏着必然”.自然界很多现象是一种随机现象,但其中的规律需要人们去探寻,无论是“浦丰通过投针计算圆周率”,还是“孟德尔通过豌豆获得遗传规律”都是坚信其存在必然性的前提下获得的.而当找出其中的规律后又应及时引导学生分析某一事件发生的偶然性,从而让学生感受到其中的哲学意蕴.
结语:数学与哲学是密不可分的.数学教育的根本目的是“提升学生的数学素养,引导学生会用数学眼光观察世界,会用数学思维思考世界,会用数学语言表达世界”[18],具备了数学眼光也就是形成了数学观念,而数学观念就是一种“认识客观世界的哲学思想”[19].另一方面,数学学习的过程总是在一定的观念支配下进行的,实践证明将数学教学与相应的哲学观念有机融合有利于学生形成正确的哲学观,而这些观念(即使是模糊的)对其后续学习也有很大的指导作用.
