不同浓度下V掺杂Mg2Si的第一性原理研究

梁 前， 谢 泉， 王熠欣， 罗祥燕

(贵州大学 大数据与信息工程学院 新型光电子材料与技术研究所， 贵阳550025)

1 引 言

近年来，Mg2Si半导体材料由于其良好的光学特性、电学特性和力学性质赢得了材料学界的广泛关注. Mg2Si是一种环境友好型半导体材料，具有无毒无害、对环境无污染、较大塞贝克系数、低热导率、价格低廉、实用性强等优点. 基于硅基上生长的Mg2Si薄膜材料可以与传统Si工艺兼容，相对于其他材料，Mg2Si可能更适合于应用于目前的集成工业技术中，人们对Mg2Si材料的研究从未停止. 因掺杂可以使半导体材料具备了本征材料不具备的优良特性，故掺杂也通常作为一种常用的手段来进行光电性质和其他性质的调控方式. 例如，Zhang等人[1]通过包晶反应，成功制备出Mg2X(X=Si,Sn)环境友好型热电材料，又对其进行La掺杂的研究发现，La的掺杂显著地提高了Mg2X(X=Si,Sn)材料的热导率复合材料的电导率和热导率；Xiao等人[2]通过Sb掺杂Mg2Si发现：Sb元素的引入可以显著提高Mg2Si材料的强度和塑性；Dai等人[3]向Mg2Si体系掺入稀土元素La和Ce之后发现La和Ce掺杂之后可以明显改善Mg2Si的力学性能，电子轨道杂化形成的共价键增强了材料的强度；Sakamoto等[4]的计算结果表明Al和Bi共掺杂Mg2Si和纯Bi掺杂都可以提高Mg2Si的热电优值，Al和Bi共掺杂获得了比纯Bi单掺更高的热电优值，减少了有毒元素Bi的使用，可以完美替代纯Bi元素掺杂Mg2Si，而Cu和Ag元素的掺杂在实现热电转换方面存在不足. 鉴于国内外对于过渡金属元素V元素掺杂Mg2Si材料的研究文献极少，基于此，该文首次通过CASTEP模块对V掺杂模型Mg2-xVxSi(x=0，0.25，0.5，0.75)进行了电子结构和光学性质的计算，为Mg2Si材料在电子器件和光学器件方面的应用提供了理论依据.

2 理论模型与计算方法

2.1 理论模型

Mg2Si是Mg-Si化合物中唯一可以稳定存在的化合物，Mg2Si晶体属于周期表第Ⅱ、Ⅳ族元素化合物半导体. Mg2Si的原胞结构和晶胞结构如图1所示，其中黄色小球代表Si原子，绿色小球代表Mg原子，Si原子占据立方体的8个顶角和6个面心，晶体学占位为8c(0.25，0.25，0.25)位，Mg原子占据由大立方体分割成的8个小立方体的中心位置，晶体学占位为4a(0，0，0)位. Mg2Si的晶格常数a=6.35 Å，键角α=β=γ=90°，Mg原子和最近邻Si原子之间的距离为2.77 Å，属于立方反萤石结构(CaF2)，空间群为Fm3m(第225号空间群).

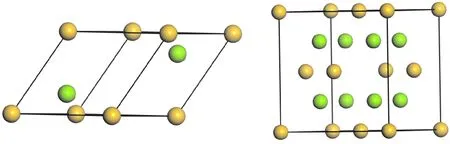
图1 Mg2Si的原胞和晶胞模型Fig. 1 Primitive cell and conventional cell of Mg2Si.

2.2 计算方法

密度泛函理论(Density Functional Theory)[5,6]是一种基于量子力学的从头计算(Ab-initio)理论，本文的全部结果是通过Materials Studio软件中CASTEP(Cambridge Serial Total Energy Package in Material Modeling, Accelrys)[7,8]模块计算得到. 计算选取Mg2Si原胞为基体，建立四个2×1×2超胞，采取替位式掺杂的方法，分别采用0个、1个、2个、3个V原子替代相应个数Mg原子，建立了四种V掺杂模型Mg2-xVxSi(x=0，0.25，0.5，0.75).

3 结果与分析

3.1 晶格常数和体积

表1列出了在结构优化后的4种Mg2-xVxSi(x=0，0.25，0.5，0.75)模型的晶格常数，本征Mg2Si的晶格常数实验值为6.35 Å[11]，而优化后的本征Mg2Si计算模型的晶格常数值为6.36 Å，与实验值偏差仅仅为0.15%，证明了此掺杂模型和计算结果的可靠性和合理性. 由表1可以看出，晶格常数和体积随着V元素掺杂浓度的升高而减小，这是由于V的原子半径小于Mg的原子半径所造成的.

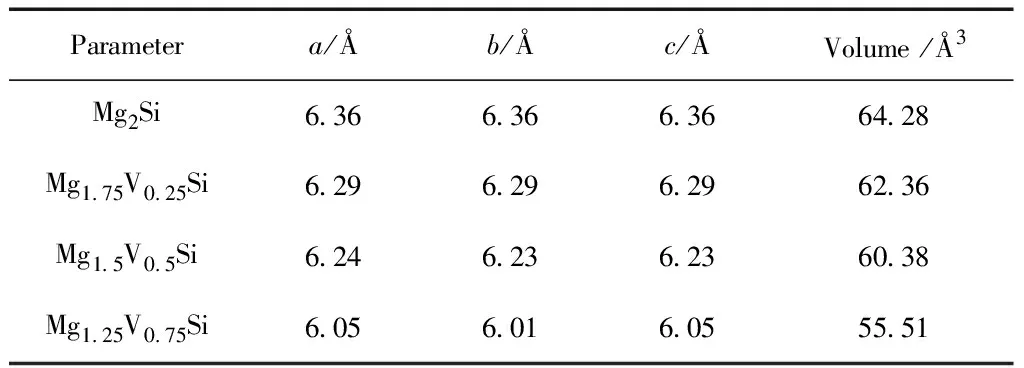
表1 结构优化后的Mg2-xVxSi折合晶格常数

3.2 能带结构

图2(a)为计算所得本征Mg2Si原胞的能带结构图，上自旋与下自旋能带图一致，表明本征Mg2Si为非磁性材料. 能带结构图显示，价带顶位于高对称点Γ点处，导带底位于高对称点F处，Mg2Si导带底和价带顶处于不同的K点处，和半导体Si、Ge一样，同属于间接带隙半导体，这与M.Y.Au-Yang[12]计算所得一致. 计算结果表明，本征Mg2Si的带隙宽度为0.209 eV,计算所得带隙较实验值0.77 eV偏低[13]，这是由于GGA近似下的PBE方法通常会低估能带带隙所致[14],这也是许多文章的共性问题[3,4,15,16]，但这并不影响我们对Mg2Si进行定性分析.

图2(b)、(c)、(d)分别为几种不同浓度V掺杂之后Mg2-xVxSi的能带结构图. 由图可以看出，上自旋在费米能级附近，导带和价带发生交叠，而下自旋在费米能级附近，导带和价带不交叠，产生了带隙. 这是由于V的掺杂作用，Mg2Si由其原本的半导体性变为半金属性(half-metal)，在费米能级附近能带线条增加，出现了杂质能级，电子跃迁所需能量降低，使其导电性变好，该特性可应用于电子器件领域的许多方面.

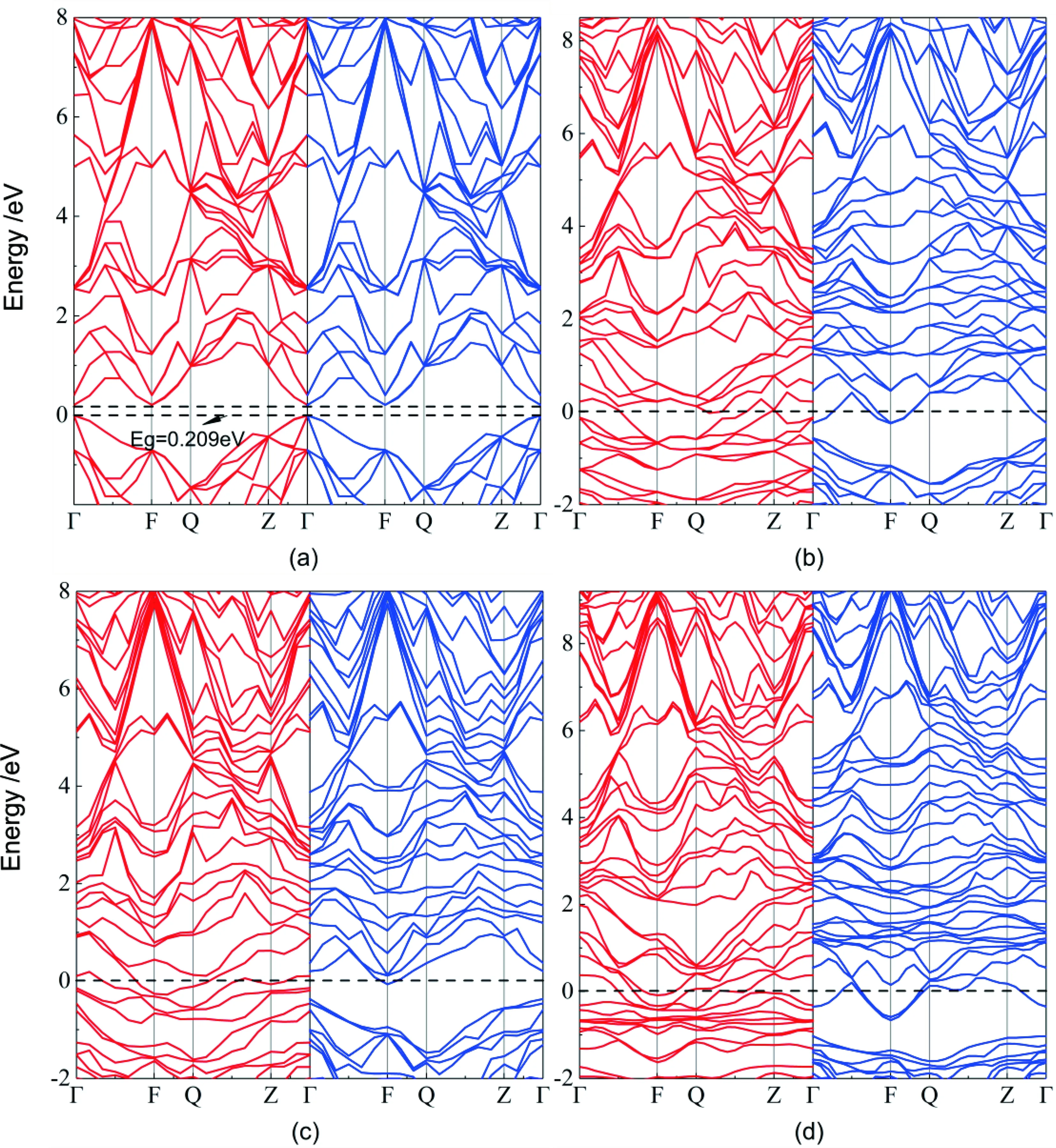
图2 Mg2-xVxSi的能带结构 (a) Mg2Si的能带结构(b) Mg1.75V0.25Si的能带结构(c) Mg1.5V0.5Si 的能带结构(d) Mg1.25V0.75Si的能带结构Fig. 2 Band structures of Mg2-xVxSi: (a) Band structure of Mg2Si,(b) Band structure of Mg1.75V0.25Si,(c) Band structure of Mg1.5V0.5Si,(d) Band structure of Mg1.25V0.75Si.

3.3 态密度

态密度是描述原子中电子能量的分布情况的物理量，能量介于E～E+ΔE之间的量子态数目ΔZ与能量差ΔE之比，即单位频率间隔之内的模数,定义为：

图3(a)为未掺杂时本征Mg2Si的态密度图(x=0)，由图可以看出，上自旋和下自旋态密度图呈现出上下对称的特性，费米面附近没有发生自旋劈裂的现象，表明本征Mg2Si为非磁性材料，这与本征Mg2Si能带图显示出的特性一致.

图3 (b)、(c)、(d)分别为几种不同浓度V元素掺杂之后Mg2-xVxSi的能带结构图. 结果显示，在掺入V元素之后，上自旋和下自旋态密度图呈现出上下不对称的特性，费米面附近发生了自旋劈裂的现象，表明V元素的引入使得Mg2-xVxSi具有了磁性，这主要是V元素属于顺磁性元素，V元素会产生局域磁矩导致原本无磁性的Mg2Si产生了磁性.

掺杂前，在-10 eV到-5 eV之间，Mg的2p轨道和Si的3s轨道占据主导地位，在靠近费米能级附近(-5 eV～5 eV)，主要由Mg的2p、3s轨道和Si的3p轨道共同贡献. 在掺杂后，在-10 eV到-5 eV之间，仍是由Mg的2p轨道和Si的3s轨道占主导地位，在靠近费米能级附近，主要由Mg的2p、3s轨道、Si的3p轨道和V的3d轨道共同贡献，在其余能级处，V元素贡献极低. V元素的掺入前，DOS图在费米能级附近较为平均、没有局域尖峰，V元素掺入后，费米能级附近出现了很大的尖峰，这是由于V元素的3d轨道的作用.

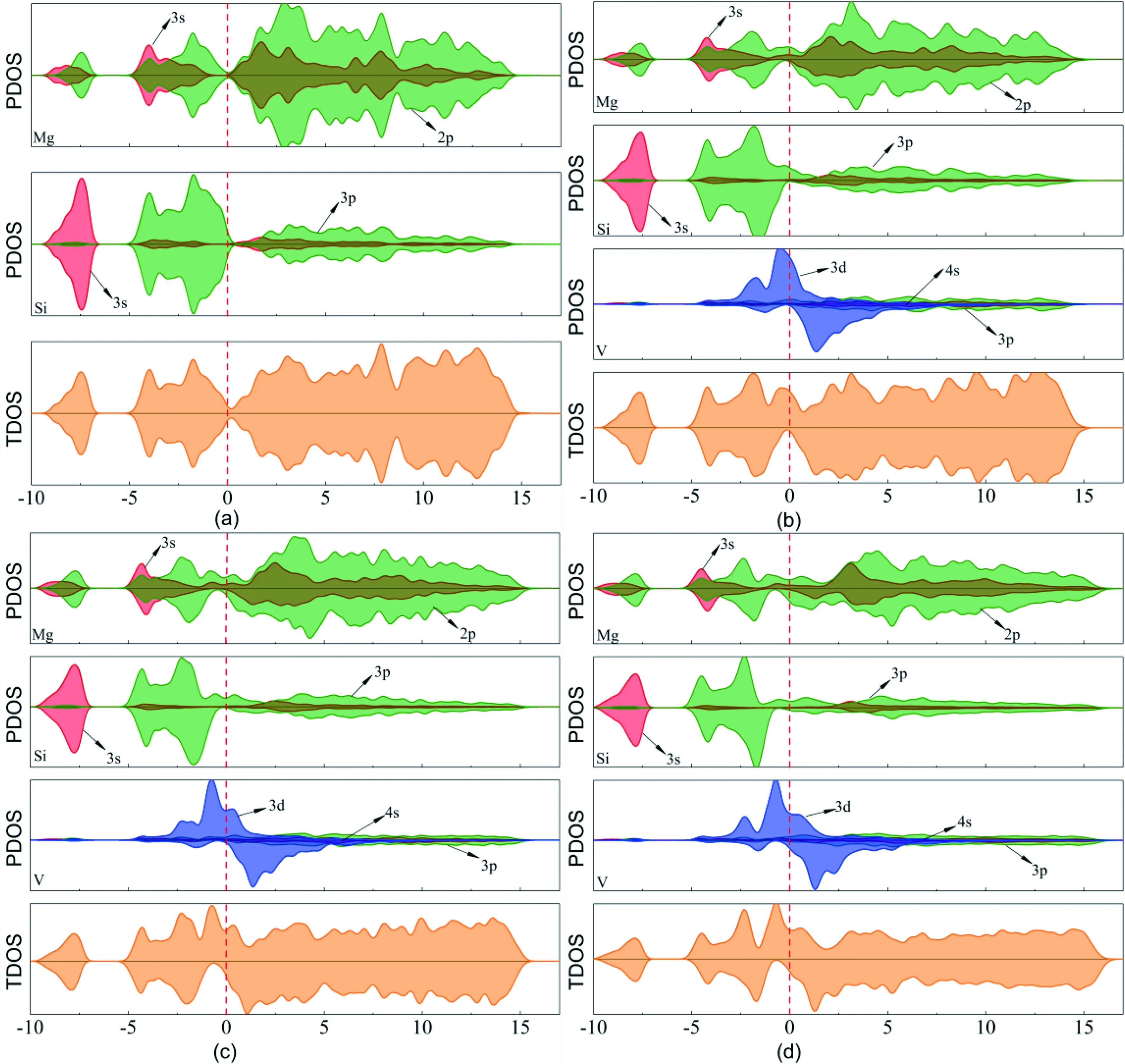
图3 Mg2-xVxSi的态密度图 (a) Mg2Si的态密度图(b) Mg1.75V0.25Si的态密度(c)Mg1.5V0.5Si 的态密度图(d) Mg1.25V0.75Si的态密度图Fig. 3 DOS of Mg2-xVxSi: (a)DOS of Mg2Si,(b)DOS of Mg1.75V0.25Si, (c) DOS of Mg1.5V0.5Si,(d) DOS of Mg1.25V0.75Si.

3.4 光学性质

光学性质是材料十分重要的性质之一，材料的光学性质通常用一些称作光学常数的物理量来描述，掺杂通常会引起材料光学性质的改变. 本文主要计算了不同浓度V掺杂后Mg2-xVxSi的复介电函数、光吸收系数和光反射率.

3.4.1复介电函数

材料的复介电函数通常可以由下面公式描述：

ε(ω)=ε1(ω)+iε2(ω)

实部ε1(ω)实际代表了束缚电子对介电常数的贡献，实部越大表明体系对电子的束缚能力越强. 虚部ε2(ω)代表损耗，虚部和电导有关，虚部越大，自由电子的电导率则越大，绝缘性就越差.

图4(a)为计算得出的Mg2-xVxSi复介电函数的实部的图像，当光子能量为0时对应的实部表征的是静态介电常数. 由图4(a)可以看出，在本征Mg2Si对应的静态介电常数值约为22.8，在x=0.25和x=0.5时对应的静态介电常数值分别约为49.6、43.8，而x=0.75时对应的静态介电常数值高达93.2. 与本征Mg2Si进行比较发现，在V元素掺杂后静态介电常数都变大，其中Mg1.25V0.75Si 所对应的静态介电常数最大.

图4(a)表明，四种模型的函数图像在低能量区域(0～6 eV)出现明显差异，而在高能量区域几乎没有差异. 光子能量在0.8～2.5 eV区域内，复介电函数的实部数值随着掺杂浓度的升高而降低；光子能量在2.5～6 eV区域内，复介电函数的实部数值随着掺杂浓度的升高而增大；随后四条曲线趋于一致.

图4(b)为计算得出的Mg2-xVxSi复介电函数的虚部的图像. 由图6(b)可以看出，四种模型的函数图像在低能量区域(0～8 eV)出现明显差异，而在高能量区域几乎没有差异.

由于V元素的掺杂作用，虚部由原来未掺杂的一个介电峰逐渐变为两个介电峰，介电峰分别产生在0～1 eV和2～3 eV之间，第一介电峰值随着掺杂浓度的升高而逐渐增大，区域内整体上呈现出数值增大的趋势；第二介电峰随着掺杂浓度的升高而逐渐增大，区域内整体上呈现出数值减小的趋势；在8 eV以后，逐渐减小为0并且四条曲线趋于一致.

图4 Mg2-xVxSi复介电函数 (a)复介电函数的实部 (b) 复介电函数的虚部Fig. 4 Complex dielectric functions of Mg2-xVxSi:(a) Real part of the complex dielectric function, (b) Imaginary part of the complex dielectric function.

3.4.2光吸收系数

光吸收系数α定义为：

α=4πk/λ=2ωk/c

其中k为消光系数，λ为波长，ω为频率.

图5为计算得出的Mg2-xVxSi的吸收光谱图，图中0～20 eV对应于本征吸收区，在无掺杂时，本征吸收峰可达240000 cm-1，20～35 eV区间吸收系数几乎为0，该区间对应于自由载流子吸收,说明对35～62 nm紫外波段的光几乎无吸收，35～45 eV对应于晶格吸收区,45～60 eV对应于杂质吸收、磁吸收等.

由图5可以看出，V元素掺杂后，本征吸收峰值出现略微下降， 相比本征吸收峰，晶格吸收峰变化较大，晶格吸收峰值随着掺杂浓度的增加而增加, 45～60 eV区间几乎无变化，最后吸收系数随着光子能量的增加而逐渐变为0.

图5 Mg2-xVxSi的吸收光谱Fig. 5 Absorption spectra of Mg2-xVxSi.

3.4.3光反射率

当光入射到两种物质的交界面上时，会发生光的反射现象，当光从真空(空气)正入射至固体表面时，此时反射比R(ω)定义为：

它表示的是反射功率和入射功率的比值.

图6为计算得出的Mg2-xVxSi的反射光谱图，由图可看出，本征Mg2Si分别在4.7 eV、10.3 eV附近出现两座反射峰，峰值分别为0.72、0.82. 反射率随着掺杂浓度的不断加大而明显下降，反射峰值也随之减小，表明其穿透率变大,可以更好地应用于一些光学器件中.

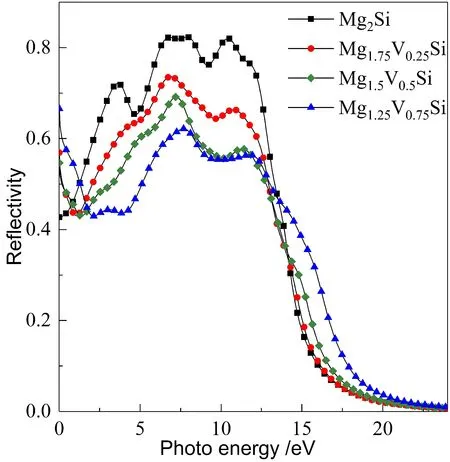
图6 Mg2-xVxSi的反射光谱Fig. 6 Reflectance spectra of Mg2-xVxSi.

4 结 论

通过第一性原理平面波赝势的方法，创新性地使用了不同浓度V掺杂Mg2Si材料，并且计算了掺杂之后的电子结构和光学性质. 计算结果表明，V掺杂之后会使Mg2Si由其原本的半导体性变为半金属性，在费米能级处出现了杂质能级；在态密度图分析中，掺杂后态密度图由原来的上下对称结构变为不对称结构，在费米能级处出现了局域尖峰，其原因主要由V元素的3d轨道电子在费米能级附近的贡献作用导致；复介电函数的实部在低能量区域(0～6 eV)出现差异，虚部在低能量区域(0～8 eV)出现差异，而在高能量区域几乎没有差异；在低能量区域吸收系数略有下降，高能量区域吸收系数上升；光的反射率随着掺杂浓度的提高整体向下偏移.