二组元置换式面心立方固溶体晶格畸变的晶体学模拟
2022-04-12孙宇菲王晓阳朱会敏
张 钧, 孙宇菲, 王晓阳, 王 楠, 朱会敏
(沈阳大学 机械工程学院, 辽宁 沈阳 110044)
近年来, 在材料科学领域关于金属合金化的研究越来越广泛, 而且在工业生产及人们生活中金属合金化的应用也越来越宽泛[1]。 合金化元素原子置换基体点阵原子形成置换式固溶体是实现材料多元合金化从而提高硬度强度的主要途径之一[2-4]。 一般来讲,添加合金化元素势必会引起基体点阵的晶格畸变[5], 并且有时添加多个组元对多元合金的硬度并没有明显改善。 为了解晶格畸变所引起的固溶强化对多元合金的强化作用, 可以通过其他工艺参数的优化调整来实现合金形貌组织、致密度等方面的一致性。 在此条件下, 由于合金成分的变化所引起的晶格畸变则成为合金硬度强度提高的主要原因[6]。
在面心立方固溶体合金中,最常见的晶面为(200)、(220)及(111)面,各个晶面的短程结构如图1所示,其中最密排晶面为(111)面,该晶面的原子堆积方式最紧密,空隙最小,结构具有很强的稳定性。
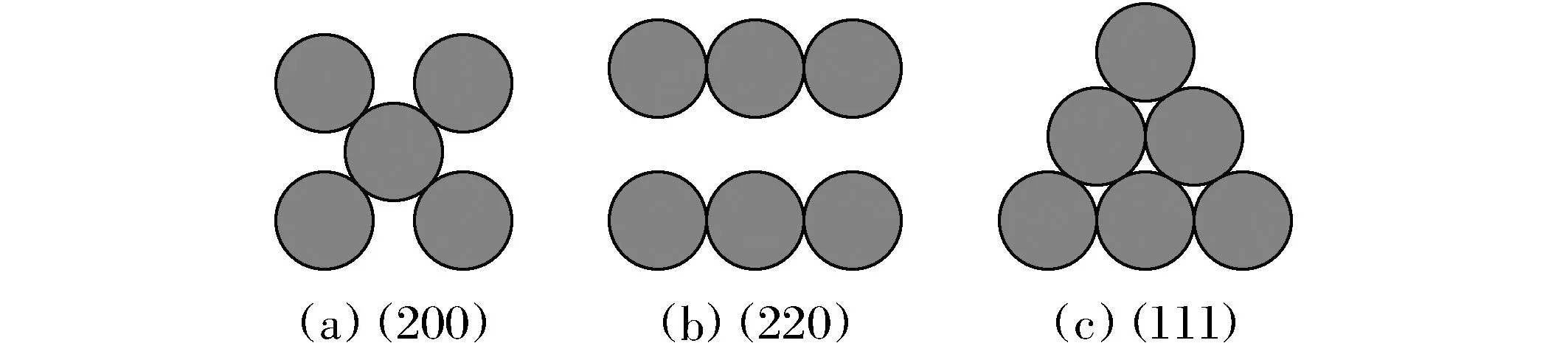
图1 不同晶面的原子排列短程结构
本研究采用计算机模拟方法,通过对面心立方晶体点阵的(111)晶面进行模型化试验,直观表征不同合金成分下各组元原子的排列方式变化,给出合金中晶格畸变的演变特征,进而定量考查不同合金成分下晶格畸变的变化规律。
1 模型构建与相关计算
1.1 模型构建及模拟工具选择
以置换式面心立方固溶体的晶体学知识为基础,采用刚性球原子模型进行面心立方(111)晶面的二维结构模拟,主要考查由于不同元素的原子半径尺寸差别而引起的位错及晶格畸变,不掺杂其他能量因素。
具体实施步骤如下:采用刚性球原子模型,在Python软件条件下,进行单一组元面心立方典型晶面(111)面原子分布模拟;再进行二组元面心立方(111)面原子分布晶格模拟,通过建立随机函数来控制各合金组元的成分变化,实现二组元面心立方固溶体(111)晶面晶格模拟;通过改变二组元固溶体的组元相对值,计算固溶体晶格的空隙率、晶格常数以及晶格畸变率;最后进行总结分析,建立成分对晶格畸变的影响特征规律。
1.2 模型建立及相关计算过程
设置多组不同摩尔比的二组元固溶体进行晶格模拟,按照一定的组元配比进行分配,其中基体原子为溶剂原子,置换原子为溶质原子。溶剂原子与溶质原子的相对原子百分比(原子数目比)简称原子比,按照设定的百分比考虑。利用Python程序对所有原子进行随机排列,要求符合置换式面心立方固溶体(111)面的原子分布特点,即刚性球面相切排列。先设定中心原子为0,为简单区分起见,其他位置上的合金元素原子设为1、2两种原子,计算程序分为以下5个步骤:
1) 输入组元原子半径值R1、R2,再指定最近邻配位层上原子1的个数N1和原子2的个数N2。
3) 这时则产生一系列原子1和原子2按照预先设定比例进行均匀分布的随机数,确定N1个原子1、N2个原子2在最近邻配位层的具体位置。
4) 在此基础上,进行次近邻配位层原子的排列,直至次近邻配位层排满,晶体结构达到最紧密状态,此时下次排列的初值取本次得到的NT值。
5) 重复上述步骤15~20次,直至所得到的各个NT稳定,则原子排列达到稳定的最紧密状态。
以上各步中,在配位层排满原子的方法借鉴于汪文川等[7]的原子排列方法。
在刚性球原子模型中,原子间的空隙面积随置换原子的增加也随之变化,空隙面积与总面积的比称为空隙率,用Φ表示:
在理想化的固溶体中,Vegard定律给出了连续固溶体的晶格常数a与组元之间的关系[8],可以表示为
a=x1a1+(1-x1)a2。
式中:a是Vegard定律计算得到的固溶体晶格常数,nm;x1是金属组元1在固溶体中的原子比,%;a1和a2分别是固溶体中2个合金组元的晶格常数,nm。
考虑理想化的(111)面刚性球原子模型,原子半径和晶格常数具有下面关系,即
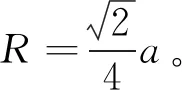
(1)
式中,R表示金属组元的原子半经,nm。
由式(1)可知,晶格常数a的变化与原子半径有较大关系。然而,刚性球原子的排列缺陷同样会影响晶格常数a,即刚性球原子排列点阵中的填隙缺陷变大,则其晶格常数增大;反之,当空位缺陷变少,晶格常数变小。
在本研究的模型中,可以利用Python程序直接计算出等效平均原子半径R′,由等效平均原子半径R′再求得晶格常数a′。将本模型中的晶格常数a′与Vegard定律中晶格常数a相比得出晶格畸变率σ,晶格畸变率σ可表示为
式中:σ为晶格畸变率;a′是通过Python程序模拟间接计算得到的晶格常数,nm。
晶格畸变有不同的表示方法,原则上要和标准状态或者理想化状态的晶格数据进行比较。例如,刘建路等[9-10]和尹荔松等[11]在研究中对晶格畸变率的计算,是用平均晶面间距与标准晶面间距相比来表示的。
考虑到实际的应用对比,模拟刚性球堆积点阵模型共设置了3组置换式面心立方固溶体模型,分别为钛-锆(Ti-Zr)、钛-铝(Ti-Al)和锆-铝(Zr-Al)合金体系。以Ti-Zr为例,每组选取一定数量的组元原子按照一定的组元配比进行分配,其中Ti为溶剂原子,Zr为溶质原子,溶剂原子与溶质原子的原子比分别为90∶10、80∶20、70∶30、60∶40、50∶50、40∶60、30∶70、20∶80、10∶90。利用Python程序对所有原子按照比例进行随机排列,按照预设的程序运行,并且要求符合置换式面心立方固溶体(111)面的晶体点阵结构特点。
2 结果与分析
2.1 晶格点阵及晶格畸变
以Ti-Zr固溶体为模拟对象的晶格畸变示意如图2所示,Ti-Zr晶体点阵随着Zr原子比的增加,原子间的空隙比纯Ti原子排列时增加,但随着Zr原子比的增加,晶格点阵并不能完全表现出面心立方(111)面特征,部分区域由于原子错位产生了晶格畸变,晶体结构也发生了变化,开始由(111)面向(200)面,甚至是(220)面转变。图3为Ti-Zr固溶体晶格的短程结构示意,当Ti和Zr原子比为40∶60和70∶30时,短程结构已经开始呈现(200)面晶格排布特点,但大部分点阵区域仍保持着(111)面的结构特点,如图3(a)、图3(b)所示。但是,当Zr原子比增加到一定比例时,晶格点阵又开始向(111)面转变,如图3(c)所示,这是因为晶格畸变导致的原子排列结构发生变化,继而择优取向也发生了变化。

注: —Ti原子; —Zr原子

注: —Ti原子; —Zr原子
以Ti-Al固溶体为模拟对象的晶格直观结果与Ti-Zr固溶体晶格相似,随着Al原子的增加,原子间的空隙比纯Ti相时有所增加,同时,由于Ti、Al的原子半径尺寸差别不大,晶格点阵并没有非常明显的错位和晶格畸变,只是有一些由面心立方(111)面向其他晶面转变的趋势,但整体仍保持着面心立方(111)面的晶体结构不变。图4为Ti-Al固溶体晶格的短程结构示意,当Ti和Al的原子比为60∶40时,短程结构有向(200)晶面转变趋势,但大部分结构仍保持(111)面的晶体结构不变。
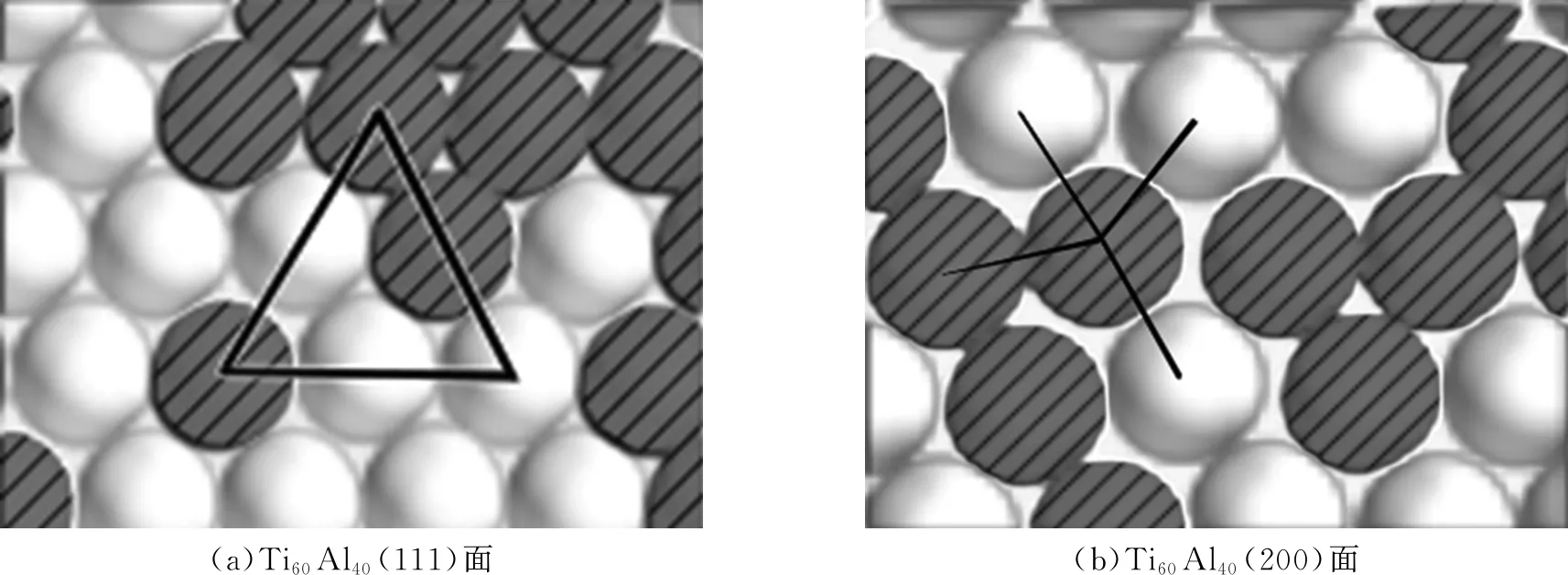
注: —Ti原子; —Al原子
以Zr-Al固溶体为模拟对象的晶格直观结果同样与Ti-Zr固溶体晶格相似,随着Al原子的增加,原子间的空隙也比纯Zr相时增加,同时,随着Al原子比的增加,晶格点阵并不是完全的面心立方(111)面,部分区域由于原子错位产生了晶格畸变,晶体结构发生了变化,择优取向开始由(111)面向(200)面甚至是(220)面转变。图5为Zr-Al固溶体晶格的短程结构示意,当Zr和Al的原子比为30∶70时,部短程结构为(200)面晶格排列特点,当Zr和Al的原子比为50∶50时,保持着(200)面晶格排列特点,但局部结构仍然保持(111)面的排列特点。

注: —Zr原子; —Al原子
2.2 二组元固溶体晶格点阵空隙率与晶格常数
Ti-Zr、Ti-Al、Zr-Al固溶体合金的空隙率变化曲线如图6所示。从图中可以看出,Ti-Zr的空隙率基本在0.170~0.178范围内波动,随着Zr原子比的增加,Ti-Zr空隙率变化非常小,但比纯Ti的空隙率高出1倍;Ti-Al固溶体的空隙率基本在0.116~0.142范围内波动,且各点的空隙率均高于纯Ti的空隙率,空隙率随着Al原子比的增加呈先上升后下降的趋势变化,但在Al原子比为40%时,由于原子错位使其晶格点阵更致密,所产生的空隙率反而变低;Zr-Al固溶体的空隙率基本在0.173~0.177范围内波动,空隙率随着Al原子比的增加,整体变化比较平缓,变化范围只有0.004,但仍然明显高于纯Zr的空隙率。整体来看,原子半径差别较大的二组元固溶体具有较大的空隙率,说明原子间空隙较大,晶格畸变量较大;而对于Ti-Al固溶体,组元之间的原子半径差别较小,相对于单一组元空隙率的变化较小,但是会出现空隙率随着成分的改变而变化的特征,即2个组元比例相近时的空隙率明显大于组元比例相差较大时的空隙率。

图6 Ti-Zr、Ti-Al、Zr-Al固溶体的空隙率变化曲线
Ti-Zr、Ti-Al、Zr-Al固溶体的晶格模拟所得的晶格常数a′与Vegard定律计算所得到的晶格常数a对比,如图7所示。总体来看, 模拟得到的晶格常数a′整体都高于Vegard定律得到的晶格常数a。这些结果与氮化物膜的实际研究是一致的。比如,在Ti-Zr-N, Ti-Cr-N硬质膜体系的研究中均发现,TiN和ZrN的固溶体及TiN和CrN的固溶体的点阵常数均高于Vegrad定律的计算结果,并且和本研究中的晶格常数变化趋势一致[12-14]。对于Ti-Zr体系,随着Zr原子比的增加,晶格常数a′增大,但Zr原子比在30%~60%时,晶格常数a′变化幅度较小;对于Ti-Al体系,晶格常数随着Al原子比的增加而减小,由于Ti、Al原子半径尺寸差较小,晶格常数a′整体变化趋势相对比较平稳,只有Al原子比在30%和50%时,晶格常数a′变化高出整体变化趋势,这是由于原子半径尺寸差造成的;对于Zr-Al体系,晶格常数a′随着Al原子比的增加而减小,Zr、Al原子半径尺寸差较大,但晶格常数a′整体变化趋势依然比较平稳。Al原子比在90%时,晶格常数a′变化低于整体变化趋势,这是由于Zr、Al原子半径尺寸差较大,Al原子比较高时,晶格常数趋于纯Al的晶格常数造成的,但对(111)面的整体结构影响并不大。
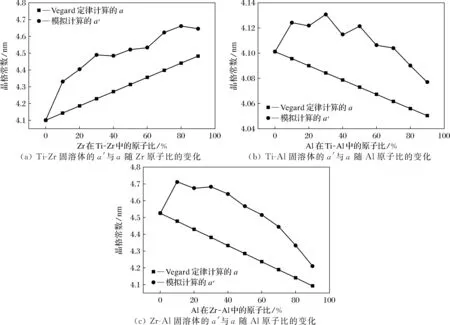
图7 Ti-Zr、Ti-Al、Zr-Al固溶体模拟晶格常数与Vegard定律计算结果对比
Ti-Zr、Ti-Al、Zr-Al固溶体的晶格模拟所得的晶格畸变率变化曲线如图8所示。对于Ti-Zr体系,晶格畸变率整体在1.035~1.062范围内变化,随着Zr原子比的增加,晶格畸变率呈先上升后下降再上升再下降的趋势变化,Zr原子比在30%时晶格畸变率最高,在90%时晶格畸变率相对来说最低。对于Ti-Al体系,晶格畸变率整体在1.006~1.012范围内变化,随着Al原子比的增加,晶格畸变率呈先上升后下降再上升再下降的微弱变化,Al原子比在50%时晶格畸变率最大,此时由于晶格错位,空隙率增高导致的晶格常数比较高,继而晶格畸变率出现最大值。对于Zr-Al体系,晶格畸变率整体在1.028~1.072范围内变化,随着Al原子比的增加,晶格畸变率呈先上升后下降的趋势变化,Al原子比在40%时晶格畸变率最高,在90%时晶格畸变率相对来说最低。整体来看,随着原子半径差的减小,固溶体晶格畸变率具有明显变小的特征。
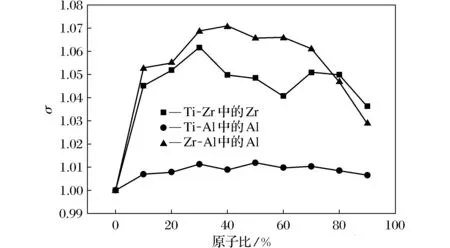
图8 Ti-Zr、Ti-Al、Zr-Al固溶体的晶格畸变率变化曲线
3 结 论
1) 对于刚性球原子模型而言,置换式二组元面心立方固溶体的(111)晶面的原子排列点阵随着某一组元的原子比例的增加,更易于发生晶格畸变,进而在某些畸变局部区域形成(200)或者(220)晶面的原子排列。
2) 当两个组元的原子半径差别较大时,晶体点阵的空隙率较大,且不随着两组元的比例变化而发生明显变化;当两个组元的原子半径差别较小时,晶体点阵的空隙率相对较小,且在两个组元比例相近时的空隙率大于组元比例差别较大时的空隙率。
3) 刚性球原子模型下,二组元固溶体的晶格常数均高于Vegard定律所得到的晶格常数,并且晶格畸变率随着两个组元原子半径差值的减小而减小。
