Cl-在α-Al2O3表面吸附的驰豫方式和溶剂化模型选择

高新宇， 祖武杰， 伍 斌， 董 瀚,2，史 文， 王 洋

(1. 上海大学 材料科学与工程学院， 上海 200444； 2. 钢铁研究总院， 北京 100081； 3. 上海大学 计算机工程与科学学院， 上海 200444)

1 引 言

铝合金由于被动氧化膜的保护在大部分环境中表现出了良好的耐腐蚀性能. 然而，部分环境中的氯离子(Cl-)等卤素阴离子会引发氧化铝膜(Al2O3)的局部降解，进而导致合金表面的点蚀，造成材料的破坏失效[1-4]. 关于Cl-与Al2O3之间相互作用的机制，目前主要有三种观点[4-7]：1)Cl-迁移/渗透到金属与氧化物界面导致局部破坏[7]；2)Cl-和O2-的竞争性吸附[8,9]；3)氧化物的破坏与修复[10]. 这些观点普遍认为Cl-与氧化膜的相互作用是点蚀形成的起始原因. 氯化物渗透到氧化膜的第一步是对表面离子的吸附，然后是进一步的迁移或反应[4,6,9,11].

用计算的方法研究Cl-在Al2O3表面上吸附的报道，目前已经有了一些. 例如，Liu等[11]和Zhang等[12]计算了Cl-在α-Al2O3(0001)和Al(111)表面内的迁移和Cl-在α-Al2O3上的吸附. Zhang等[13,14]研究了H2O和Cl-对层缺陷氧化铝的侵蚀，以及OH、Cl和H2O在层缺陷Al2O3膜上的共吸附行为. Marks等[15]计算分析了水溶液中的Cl-对羟基化α-Al2O3(001)和(100)表面的腐蚀. 这些报道做了细致的工作，从微观角度解释了相关实验现象. 然而，作为被研究对象，α-Al2O3(0001)表面模型驰豫方式的选择和水溶液模型的选用可能对计算结果造成的影响，没有被详细地评估.

离子在表面上的吸附过程会造成表面多层原子的弛豫，这可能导致部分驰豫模型(部分原子被固定的模型)的计算结果与实际产生偏差. 特别是对于α-Al2O3等离子性强的金属氧化物，长程静电效应的中断和人工偶极矩的产生可能会导致部分弛豫结构和完全弛豫结构之间的显著差异，最终造成计算结果的大幅偏差[16-18]. Al、Pt等阳离子在α-Al2O3表面的吸附计算结果表明，不同的弛豫模型会导致吸附结构和离子吸附能[16]的差异. 然而，模型驰豫方式对Cl-与Al2O3之间相互作用的影响却鲜有报道. 因此，有必要探讨Cl-在α-Al2O3表面吸附计算中的模型选择.

在铝合金等金属表面的点蚀过程中，水溶液对表面的化学/电化学反应有重要的影响. 因此，需要一种有效且准确的方法来模拟材料表面水环境. 在密度泛函理论(DFT)计算中，主要有显式溶剂化模型和隐式溶剂化模型两种处理溶液的方法. 其中隐式溶剂化模型可以较好地模拟溶剂的长程静电相互作用和平均性质，在计算和模型改进中具有良好的实用性[19].

本工作采用第一性原理的方法，计算Cl-在α-Al2O3(0001)表面的吸附行为. 通过设置不同的弛豫模型，研究弛豫方式对氧化铝表面性质和Cl-在表面吸附行为的影响. 计算考虑了真空环境和水溶液环境，将得出的计算结果与实验数据对比，评估了溶剂化模型的作用. 对于Cl-与α-Al2O3(0001)相互作用的更多研究，本文在前期的模型驰豫方式选择和溶剂化模型设置方面提供了一种可靠的思路.

2 计算方法与模型

2.1 计算方法

计算在基于密度泛函理论(Density functional theory, DFT)的VASP(Vienna ab-initio simulation package)[20]上运行. 交换关联泛函的描述基于广义梯度近似(Generalized gradient approximation, GGA)[21]的Perdew-Burke-Ernzerhof(PBE)[22]，离子-电子的相互作用采用PAW(Projector augmented wave)描述[23]. 布里渊区的k点用Monkhorst-Pack方法采样[24].

α-Al2O3单胞的优化以0.0001 eV为能量收敛标准，最终的平面波截止动能取650 eV，k点为15×5×5. 优化后的晶格参数为a=b=4.808 Å，c=13.123 Å，与其它实验[25]或计算[18]研究中的差值在1%以内. 在表面层的优化计算中，原子层数和真空层厚度的选取以α-Al2O3(0001)表面能的变化小于0.01 J/m2为标准. 所有Cl-在表面的吸附计算中，平面波截断能取 650 eV，k 点取 8×8×1. 电子自洽计算收敛的标准为10-4eV，当体系中每个原子的应力小于0.01 eV/Å时，驰豫终止. 计算首先在真空条件下运行，然后在VASPsol方法[26]模拟的水溶液环境下进行，水的介电常数设置为标准值80[19]. 为了研究弛豫方式对计算结果的影响，我们使用了固定底部六层原子的部分弛豫结构和允许所有原子驰豫的完全弛豫结构.

Cl-在α-Al2O3(0001)表面的吸附能由下式计算：

Eads,Cl=ECl/Al2O3- (EAl2O3+ECl)

(1)

其中ECl/Al2O3表示Cl-吸附到表面后体系的总能量，EAl2O3是清洁表面(未吸附Cl-的表面)的能量，ECl表示孤立Cl原子的能量.

2.2 理论模型

本文使用12层原子和15 Å真空层的(2×2)α-Al2O3(0001)表面模型. 全弛豫模型(12-R)和部分驰豫模型(12-C)如图1(a)、(b)所示. 在图1(a)中，Al1表示第一层铝原子，O2表示第二层氧原子，以此类推. 对于Cl-在表面的吸附，我们考虑了5个不同的位点，如图1(c)所示. 位点名称是以Cl-正下方的原子命名的，编号代表原子所在层数，遵循Hernández[27]的命名法.

图1 (a)完全弛豫和(b)部分弛豫的α-Al2O3(0001)表面模型侧视图；(c)Cl-吸附位点俯视图.红色原子表示O，灰色原子表示Al.Fig. 1 Side views of the (a) full relaxation and (b) partial relaxation α-Al2O3 (0001) models, and (c) top view of the adsorption sites of Cl- on the surface. The red and grey atoms are O and Al, respectively.

3 结果与讨论

3.1 弛豫方式和溶剂化模型对α-Al2O3(0001)表面结构的影响

表1统计了12-R和12-C在真空和水溶液环境下优化后的层间间距百分比变化，并列出了其它计算和实验工作中的相应变化，其中“+”表示平均原子层间距的增加，“-”表示减少. 可以看出，两种弛豫模型的原子层在真空和溶剂化条件下均有较大的弛豫量，其中d(Al1-O2)的变化值最大，第一层Al原子(Al1)向下移动到几乎与第二层O原子(O2)共面，这和其它研究中的结果相近.

表1 真空和水溶液环境下12-R和12-C的原子层层间距变化

从驰豫方式的角度来看，真空和溶液条件下，优化后的12-R和12-C模型原子层层间距发生了明显变化. 其中真空下12-C的d(O2-Al3)比12-R增大了60%；溶液环境中，12-R和12-C模型的d(Al1-O2)差值超过13%，其它的层间距也有不同程度的改变. 这些变化说明12-C模型中被固定的底层6层原子对体系最终结构有较大影响，这可能会影响到后续计算结果的可靠性.

从溶剂化模型的角度来看，真空条件下两种驰豫模型的原子层层间距值与实验值有很大差距. 而在水溶液条件下，12-R和12-C中d(Al1-O2)和d(O2-Al3)的变化量分别为-66.0%、-79.0%和+7.7%、+9.3%，更接近实验值的-51%、+16%. 对于溶液条件下两种结构的d(Al3-Al4)和d(Al4-O5)，虽然和实验值有一定差异，但是和真空条件下的结果没有显著区别，并且第4、5层原子对Cl-在外表面的吸附影响较小. 以上结果表明，在VASPsol隐式溶剂化模型下优化得到的α-Al2O3(0001)表面更接近实验结果，是较为可靠的理论模型.

3.2 弛豫方式和溶剂化模型对Cl-在α-Al2O3(0001)表面吸附行为的影响

表2统计了Cl-在真空和水溶液环境下的12-R和12-C表面不同吸附位点上的吸附能、吸附距离和吸附方式. 当吸附状态为化学吸附(cp)时，吸附距离为Cl-与被吸附原子之间的键长；当吸附状态为物理吸附(pp)时，统计的吸附距离为Cl-与第一层原子之间的平均距离.

在真空和水溶液条件下，Cl-在12-R和12-C模型上均有三种稳定吸附结构和两种吸附状态.真空条件下Cl-在12-R和12-C表面最稳定的吸附位点均为Al1(吸附结构如图2(a)和(c)所示)，吸附距离为2.14 Å，吸附能分别为-2.20 eV和-2.27 eV. 在溶液环境下，Al1位点仍然是12-R和12-C表面最稳定的吸附位点(吸附结构如图2(b)和(d)所示)，其吸附能分别为-3.05 eV和-3.16 eV，吸附距离分别为2.30 Å和2.31 Å. Cl-在所有Al3和Al4位点均为物理吸附. 在能量最小化过程中，O2和O5位上的Cl-是不稳定的，会自发地向Al1位移动，最终产生和Al1位点同样的吸附结构，这与其它计算的结果相同[12].

综合对比真空和水溶液条件下的结果可知，水环境中Cl-在所有位点的吸附距离均有一定幅度增加，吸附能有明显下降. Cl-在VASPsol方法模拟的水溶液环境中有更低的吸附能，这说明Cl-在液相环境中有更强的吸附驱动力，更容易与氧化铝表面之间发生相互作用，这与常见的腐蚀现象相符合. 此外，对于12-R和12-C模型，Cl-在真空或溶液环境中相同位点的吸附能和吸附距离均有不同幅度的区别，其中水溶液中Cl-在两种驰豫模型Al3位点上的吸附能和吸附距离相差达到30%和54%. 由此可见，在Cl-吸附到表面的计算中，采用部分驰豫的模型仍然会对结果产生较为明显的影响.

为了进一步了解Cl-与氧化铝外表面的相互作用，并研究模型驰豫方式对系统电荷分布的影响. 部分结构的电子局域函数(Electron Localization Function, ELF)和差分电荷图被展示在图3和图4中.

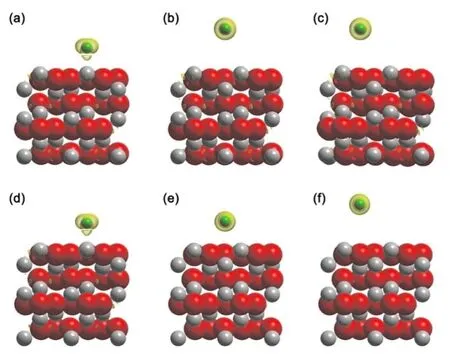
图3 水溶液条件下，12-R和12-C三种吸附结构的ELF：(a)12-R-Al1；(b)12-R-Al3；(c)12-R-Al4；(d)12-C-Al1；(e)12-C-Al3；(f)12-C-Al4.Fig. 3 ELFs of three adsorption structures of full and partial relaxations in solvation environment, (a) 12-R-Al1; (b) 12-R-Al3; (c) 12-R-Al4; (d) 12-C-Al1; (e) 12-C-Al3; (f) 12-C-Al4.

ELF被广泛用于描述分子中的化学键，其标准化数值在0到1之间.取上限值1表示电子完全局域化，0.5表示电子完全离域化[30,31].图3(a)和(d)分别是溶液条件下12-R和12-C结构Al1位点吸附Cl-的ELF，ELF值为0.856，可以看出Cl-与Al之间存在电子高度局域化区域，且其ELF值大于0.85. 图4(a)和(d)的差分电荷图也表明，在两种结构中，Cl-与氧化铝表面原子之间均存在明显的电荷交换. 这些结果表明12-R和12-C的相应结构中，Al与Cl-之间存在较强的共价键作用. 表3中统计了水溶液环境下12-R和12-C的清洁表面和Cl-吸附表面第一层四个Al和第二层三个O的bader电荷，Al和O原子的位置及名称如图5所示. 从表3中可以看出，两种驰豫结构中被吸附的Al原子(Al1(1))的bader电荷均有所增加，而第一层其它三个Al和Al1(1)附近的三个O的bader电荷则有所减小. 这一变化证明了Cl-吸附到表面Al1(1)上之后，第一层其它Al及附近O原子的电荷均向“Al-Cl”单元转移，Cl-与表面之间发生了较强的相互作用.

图3(b)、(c)、(e)、(f)中的ELF表明，在12-R和12-C的Al3和Al4位点上，Cl-和α-Al2O3(0001)表面的任何原子之间均没有电子局域化区域. 图4(b)、(c)、(e)、(f)的差分电荷图也表明Cl-和表面之间没有明显的电荷交换现象. 但是对比清洁表面，Cl-在这些位点的吸附实际上导致了第一层Al和第二层O的bader电荷减少. 这表明Cl-与表面之间存在较弱的相互作用，Cl-在表面发生了物理吸附. 值得注意的是，虽然12-R和12-C对照结构中同一原子的bader电荷值均有一定的差异，但是没有影响到对Cl-与表面相互作用分析的整体结果.

表3 水溶液条件下，12-R和12-C的最稳定吸附结构中第一层Al和第二层O的bader电荷

图5 表3中使用的原子代号示意图Fig. 5 Schematic diagram of atomic markers used in Table 3.

4 结 论

本文通过设置12-R和12-C两种模型驰豫方式，在真空和VASPsol方法模拟的水溶液条件下，计算分析了α-Al2O3(0001)的表面结构和Cl-在表面的吸附行为，得出了以下结论.

(1)固定底层6层原子的方式在真空和水溶液条件下均导致了α-Al2O3(0001)表面结构的畸变. 在后续的吸附计算中，虽然其没有对Cl-在表面的吸附方式和体系电荷变化的趋势造成影响，但是造成了具体的吸附能、吸附距离和bader电荷值差异. 在氧化铝表面的点蚀研究中，这可能会造成后续更多的计算结果偏差. 因此，本文建议使用全弛豫的表面模型.

(2)在水溶液条件下，α-Al2O3(0001)的表面结构更接近于实验测量值，且Cl-在表面有更强的吸附驱动力，这和常见的腐蚀现象相符合. 采用隐式溶剂化模型中的VASPsol方法，并设置一个合理的介电常数，是较为可靠的模拟材料表面水溶液环境的方法.